定点运动转轴唯一性与欧拉角位移矢量性讨论

徐晨昊，张亚红

（1.西安交通大学 机械学院，陕西 西安 710049；2.西安交通大学 航天学院，陕西 西安 710049）

刚体的定点运动可看成刚体绕一系列过定点的瞬时转轴的连续转动，关于定点运动的讨论是理论力学研究中的重要问题［1，2］.理论力学教材中通常先采用几何法证明达朗贝尔-欧拉定理，即定点运动刚体的任何有限位移可通过绕过定点的等效转轴的一次转动实现，再令运动时间趋于无穷小，定性地得到存在瞬时转轴的结论.几何证明法因不能确定等效转轴和瞬时转轴是否唯一而有失完整性.

目前已有文献使用几何法直接证明瞬时转轴的存在性，用反证法证明其唯一性［3］，也有文献利用解析法证明等效转轴的存在性［4］，经典理论力学教材中也包含瞬时转轴存在性的解析证明［5］.若能采用解析法进一步对等效转轴和瞬时转轴的唯一性进行论证，对于充实和完善刚体定点运动的描述将具有重要意义.

现行理论力学教材公认刚体定点运动的角速度矢量与瞬时转轴共线，通过反证法说明有限欧拉角位移具有不可换序性，从而证明了有限欧拉角位移不是矢量，不能合成为绕等效转轴旋转的角位移.同时通过特例证明无限小欧拉角位移是矢量，角速度矢量与欧拉角变化率之间的关系为

ω ＝ ψ·+θ·+φ·（1）

若能够对于式（1）进行严格的一般性证明，则可进一步完善刚体定点运动的描述，并对本部分教学工作具有很好的参考意义.

本文采用解析法，通过矩阵运算阐明等效转轴与初末状态的过渡矩阵之间的关系，进而对等效转轴的唯一性进行证明，并严格证明有限欧拉角位移不是矢量的结论.之后证明瞬时转轴的唯一性，并对无限小欧拉角位移是矢量的结论进行严格证明，同时基于该结论印证式（1）的正确性，并建立了瞬时转轴的方位与欧拉角之间的关系.

1 等效转轴与过渡矩阵的关系

设刚体做定点运动，定点为坐标原点O.［i j k］和［i′j′k′］分别为定坐标系和结体坐标系的单位方向向量，则

矩阵 A 为［i j k］到 [ i′ j′ k′]的过渡矩阵.同一个向量在这两组基底下的坐标之间的关系为

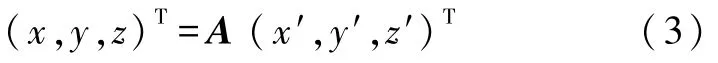
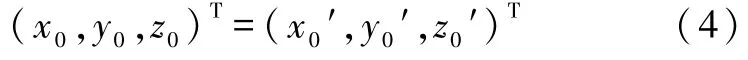
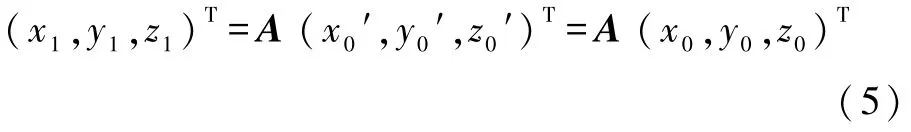
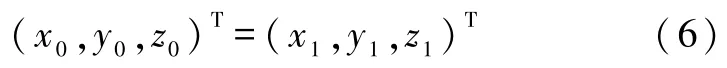
满足式（6）的向量是等效转轴的方向向量，该向量在定坐标系下的坐标向量记作e，由式（5）得

式（7）表明等效转轴的方向向量为过渡矩阵A的特征值1所对应的特征向量.

2 矩阵法证明等效转轴的唯一性

如式（2）所述，A是两组三维标准正交基 Q＝［i j k］和 Q′＝ [ i′ j′ k′]之间的过渡矩阵，满足

标准正交基构成的矩阵是正交矩阵.正交矩阵可逆，其逆矩阵和转置矩阵也是正交矩阵，正交矩阵的乘积依然是正交矩阵.由以上性质可知A＝Q-1Q′也是正交矩阵.

刚体定点运动可用图1所示欧拉角描述.设Q到Q′的欧拉角为ψ、θ、φ，则过渡矩阵A可表示为

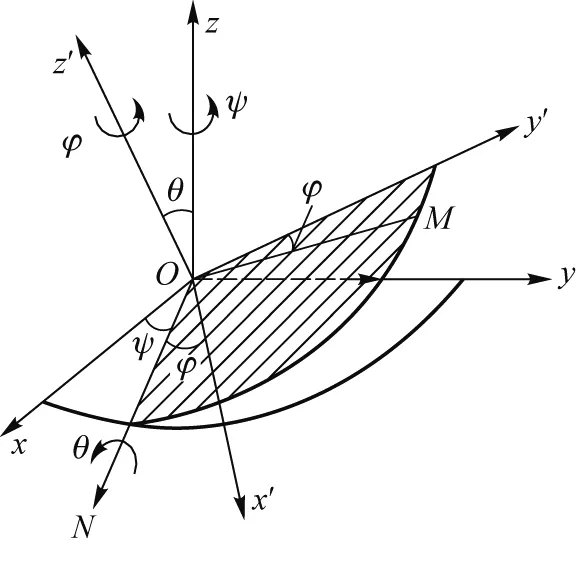
图1 欧拉角示意图

其中

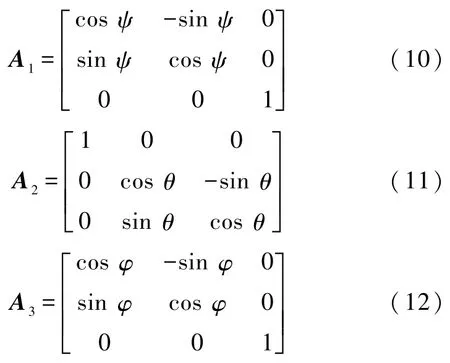
因为欧拉角与刚体定点运动的位置一一对应，所以任意一个有限位移的过渡矩阵是唯一的.经运算可知

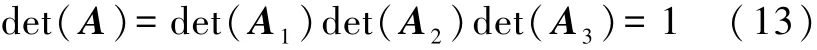
正交矩阵的特征值具有以下性质:若特征值为实数，则其必为+1或-1；若特征值为复数，则其必成对出现，且互为模等于1的共轭复数.A为三阶正交矩阵，在复数域内有三个特征值λ1、λ2、λ3，且三个特征值满足

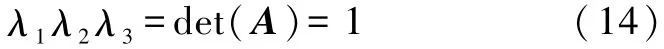
结合式（14）和正交矩阵特征值的性质分析可知，矩阵A只可能有一对复特征值或不含复特征值.当矩阵A有一对复特征值时，剩下的一个特征值必为1；当矩阵A没有复特征值时，因为A不是单位矩阵，所以三个特征值只能为λ1＝1，λ2＝ -1，λ3＝-1.由此可知，过渡矩阵 A一定有单特征值1，所以式（7）中的特征向量e存在，即等效转轴存在.

特征值 1的代数重数是指代数方程det（A-λI）＝0的根 λ＝1的重数，由上文可知其为1.特征值1的几何重数是指特征方程（7）的基础解系所含有的向量个数.根据线性代数理论可知，矩阵A的任何特征值的几何重数不大于其代数重数，又因为几何重数至少为1，所以几何重数只能等于1，即A的特征值1对应的特征向量只在一维向量空间中分布，因此等效转轴是唯一的.

至此，刚体定点运动有限位移的等效转轴的唯一性证明完毕.

3 有限欧拉角位移的矢量性讨论

刚体定点运动有限位移可以分解为进动、章动和自转.假设欧拉角位移具有矢量性，根据位移的等效性，三个欧拉角位移合成结果应当等于刚体绕等效转轴旋转的角位移.

如图1所示，进动、章动、自转的角位移分别沿z轴、节线 ON、z′轴.z轴、节线 ON、z′轴的方向向量以k、n、k′表示，则欧拉角位移在定坐标系下的表示形式为

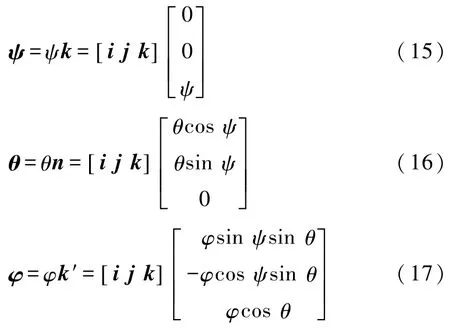
设向量 b＝ψ+θ+φ，则

根据式（9）—（12），利用 MATLAB 计算可知

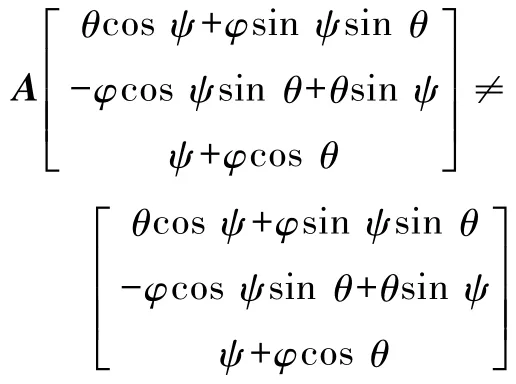
由此可见向量b不满足式（7），所以其不是该有限位移的等效转轴的方向向量.该结论与位移的等效性相违背，所以假设本身即是错误的.

综上可知，欧拉角位移不是矢量.

4 矩阵法证明瞬时转轴的唯一性

在无限小的时间间隔Δt内截取上述有限位移中的任意一段无限小位移，并且其初末状态的结体坐标系不重合.设结体坐标系在无限小位移前后的标准正交基 [ i1j1k1]和 [ i2j2k2]对应于定坐标系[i j k]的过渡矩阵分别为 B和 C，且 B＝B1B2B3，C＝C1C2C3，其中

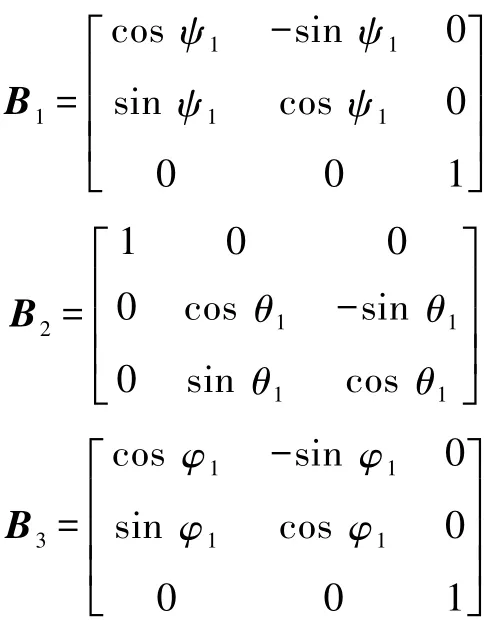
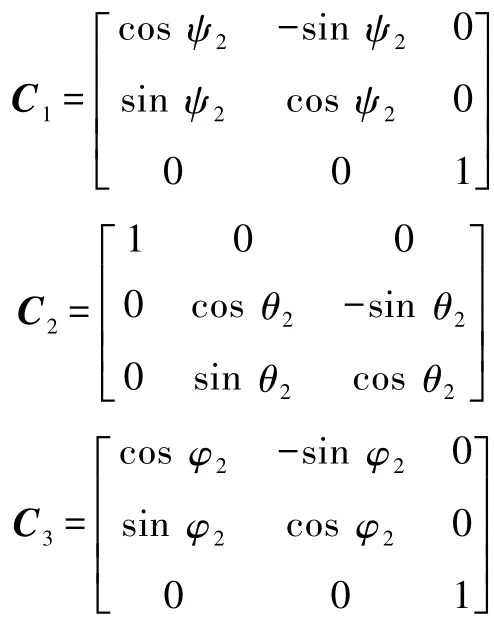
B和C满足

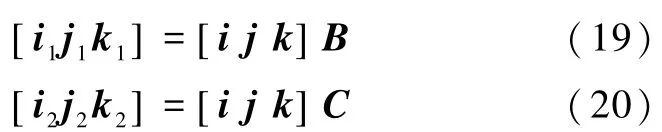
根据式（19）和式（20），设 [ i1j1k1]到 [ i2j2k2]的过渡矩阵为D，则

因为B和C皆为行列式为1的正交矩阵，所以D 也是正交矩阵，且 det（D）＝ det（BT）det（C）＝ 1.因此，依照与第2部分完全相同的证明方式可知，该无穷小位移的等效转轴是唯一的.由于 Δt→0，所以该等效转轴即为瞬时转轴.又因为该无穷小位移是任意选取的，所以刚体定点运动任意时刻的瞬时转轴具有唯一性.

5 无限小欧拉角位移的矢量性讨论

由上文可知刚体位移趋于零时满足

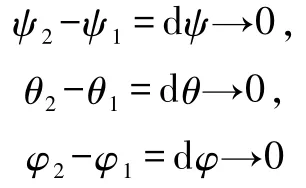
因为矩阵B的所有元素均可视作为关于ψ、θ、φ的一阶连续可导函数，所以B存在全微分

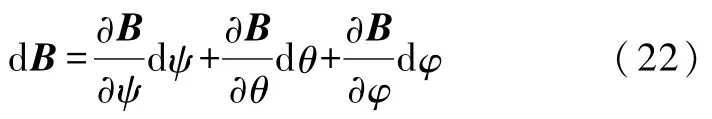
矩阵C和矩阵B无限接近，因此矩阵C可表示为

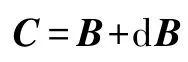
将式（22）代入上式可得

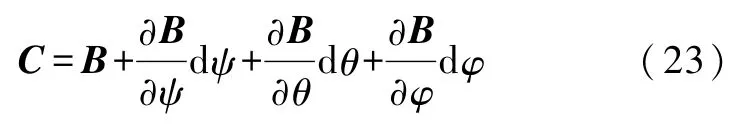
据上文所述，矩阵D＝BTC代表无限小位移的过渡矩阵，将式（23）代入矩阵 D并利用 MATLAB软件进行计算，得到过渡矩阵D的表达式，它是一个单位矩阵I与一个无穷小量矩阵 H的和.矩阵D的第一行元素为

第二行元素为

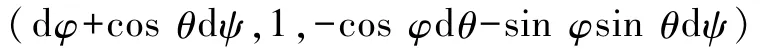
第三行元素为

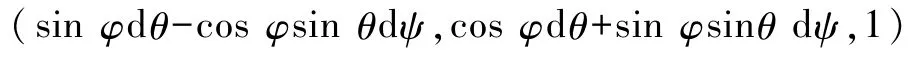
求解矩阵D的特征值1对应的特征（坐标）向量，从而得到瞬时转轴的方向向量.

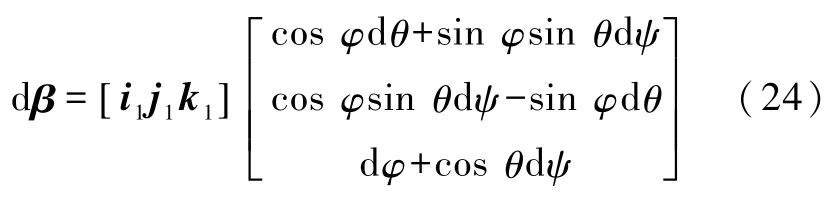
设r为坐标原点到刚体上某一点的向量，则

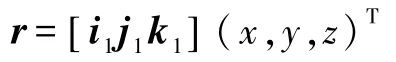
dr是其经过该无限小位移后的变化量

经MATLAB软件计算可得

由此可知dβ是该无限小位移所等效的旋转角位移.

将式（24）展开可得

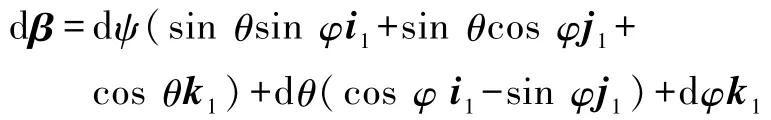
对比式（15）—（17）中的表达式，并假设无限小欧拉角位移是矢量，可得

由式（26）可知，无限小欧拉角位移的矢量和等于绕瞬时转轴的等效旋转角位移，满足位移的等效性，因此假设成立.综上所述，无限小欧拉角位移是矢量.

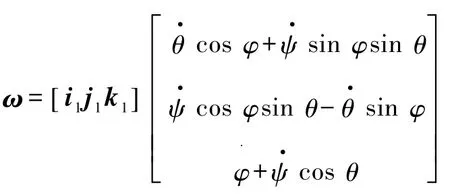
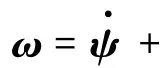
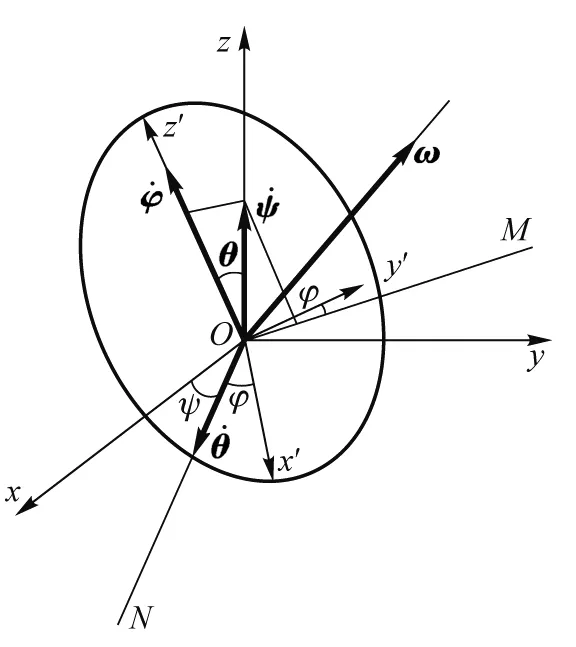
图2 刚体定点运动角速度示意图

6 结论

1）证明了刚体定点运动等效转轴的唯一性，并给出了等效转轴应满足的条件:方向向量为过渡矩阵A的特征值1对应的特征向量.

2）通过矩阵运算，论述了有限欧拉角位移不满足矢量运算的性质，从而说明有限欧拉角位移不是矢量.

3）在等效转轴唯一性的证明基础上，进一步利用矩阵及其特征值的性质，证明了刚体定点运动瞬时转轴的存在性和唯一性.

4）从角位移和角速度的定义出发，借助矩阵全微分运算，证明了无限小欧拉角位移是矢量，并建立了瞬时转轴方向向量与欧拉角之间的关系.

应当指出，上述证明和分析除了对刚体定点运动的相关结论给予严格的解析证明，分析过程也展示了矩阵及其特征值性质在复杂刚体运动分析中的优势.