任意亮度孔形衍射的数值模拟
2021-12-12方慧雯杨锦宏贺胜男卫玉娇张吴记汪卫华
方慧雯,杨锦宏,贺胜男,卫玉娇,张吴记,汪卫华
(安徽大学 物质科学与信息技术研究院,安徽 合肥 230601)
随着技术的革新,光的衍射现象在生产实践中的应用越来越广泛.多边形的衍射模拟在光学领域具有重大意义,可以解释灯光星芒产生的原因、相机如何记录图样[1]以及如何在夜晚拍出明显星芒[2].光的衍射现象可以用惠更斯-菲涅耳原理和瑞利-索末菲公式进行计算,但数学公式计算繁琐,不够直观.计算机模拟则能通过显示图像,直观地观察衍射效果.且计算机模拟不受实验场地和实验器材的限制.
目前,有很多学者已经对不同孔径的衍射现象进行了研究:比如刘有菊等研究了“E”形孔的夫琅禾费衍射现象[3],宋易知模拟了任意正多边形小孔的夫琅禾费衍射现象[4],王海涛等模拟了任意多边形小孔的菲涅耳衍射[5],Jeffrey等利用快速菲涅耳衍射算法模拟了孔形为“2”的衍射[6],Qian等研究了菲涅耳和夫琅禾费衍射的数值模拟[7],汪峰等研究了任意形状孔夫琅禾费计算机模拟[8],戴又善研究了二维小孔夫琅禾费衍射的对称变换特性[9].但已有的研究主要针对的是正多边形,不能适用于任意亮度孔形,并且现有的数值模拟不能适用任意距离.由于菲涅耳衍射和夫琅禾费衍射特性差别显著,需根据菲涅耳数进行划分[10].在上述研究的启发下,本文的创新点在于用图片像素灰度值来代表小孔内不同的亮度值;研究了任意亮度的小孔衍射;并且该程序适用于菲涅耳和夫琅禾费衍射两种情况.即采用Matlab软件,利用图片像素读取任意亮度孔形,然后对近场/远场衍射进行数值模拟,给出任意形状、任意亮度孔的衍射图案来探寻其中的衍射规律.
1 衍射的理论与数值模型
1.1 衍射理论
光的衍射现象是指光在传播过程中,遇到障碍物或小孔时,光将偏离直线传播的路径而绕到障碍物后面传播的现象[11].把波面 S上每个面积元 ds看作新的波源,如图1所示,它们均发出次波,波面前方空间某一点P的振动可以由S面上所有面积元所发出的次波在该点叠加后的合振幅来表示[12].在本文中,将小孔均分成一定数量的方格(即图像像素),像素灰度值表示孔的亮度.光屏也均分为一定数量的方格(近似将其看作一点).光屏上某一点的振动可看成小孔内所有方格点在该点的合振幅.将光屏上所有方格点的振动计算出来,就可以显示该孔的衍射图像.

图1 衍射光路示意图
设有一个波长为λ的平面波入射,衍射平面与光屏之间的距离(焦距)为 f,衍射平面上点 P(x1,y1)与光屏上点 Q(x2,y2)之间的距离为 r,根据惠更斯-菲涅耳原理复数形式:

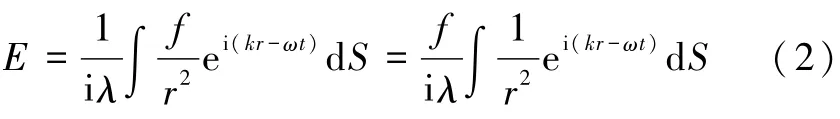
当忽略时间t时则(2)可以简化为

1.2 衍射数值模型
首先用绘图软件绘制尺寸合适的任意孔形,然后用imread函数读出所绘制的孔形,在程序中将小孔的部分设为像素灰度值,其余部分设为0,进行读取,编写程序.此程序适用于任意孔径、任意亮度、任意距离的衍射,对于不同的孔形或不同的亮度只需调换相应的孔形图片;对于不同距离的衍射,只需更改焦距f.在此基础上,调换合适的光屏大小,孔径大小,得到衍射明显的衍射图像.计算源程序附文末,程序处理小孔图像衍射的大致步骤是:1)读取任意小孔的图片;2)对衍射平面和光屏建立合理的坐标系;3)计算衍射平面和光屏上任意两点的距离;4)计算其复振幅和光强;5)画出光强图像和衍射图.
2 衍射模拟
2.1 衍射模拟与理论计算对比验证
以圆孔为例,按照半波带法,当入射光波长 λ和圆孔半径 R一定时,焦距 f变化,屏中心点O(0,0)对应的半波带数k会变化,并且该点的明暗随着k值的变化而变化.k为偶数时,为暗条纹;k为奇数时,为亮条纹.k=1是菲涅耳衍射和夫琅禾费衍射的分界点,当k>1时是菲涅耳衍射,k<1是夫琅禾费衍射.故当半波带数 k≤1时,衍射图样中心均为亮斑[11].并且从中心向外是明暗相间的圆环,且 k越大(即z越小),明暗环越多越密.k值由下式决定:

当 f=0.2 m,λ=500 nm,衍射圆孔半径 R=1 mm,光屏宽度h=0.4 mm时,由图2可见,整个光强分布以圆心为对称点,并且圆心点光强是减弱的(即产生暗斑).将数据带入式(4)计算得出 k=10,即中心光强减弱,与程序模拟相符.

图2 f=0.2 m,λ=500 nm,R=1 mm圆孔衍射光强图样
当 f=2 m,λ=500 nm,衍射圆孔半径 R=1 mm,光屏宽度h=4 mm时,由图3可见,整个光强分布以圆心为对称点,并且圆心点光强是增强的(即产生亮斑).将数据带入式(4)计算得出 k=1,即中心光强增强,与程序模拟相符.
当 f=10 m,λ=500 nm,衍射圆孔半径 R=1 mm,光屏宽度h=10 mm时,由图4可见,整个光强分布以圆心为对称点,并且圆心点光强是增强的(即产生亮斑).将数据带入式(4)计算得出 k=0.2<1,即中心光强增强,与程序模拟相符.
综上所述,理论计算结果与程序模拟结果基本一致,证明模拟程序正确.由计算可知图2是近场衍射图像,图3是近场衍射和远场衍射的分界点图像,图4为远场衍射图像.从上述图中可以得出,远场衍射图像的中央亮斑比近场衍射的亮斑大,并且随着k值逐渐减小,暗纹的光强趋于零,且在菲涅耳衍射时,中心的光强可能减弱.

图3 f=2 m,λ=500 nm,R=1 mm圆孔衍射光强图样

图 4 f=10 m,λ=500 nm,R=1 mm圆孔衍射光强图样
2.2 任意孔形及任意亮度的衍射模拟结果
运用程序数值模拟正三角形和正六边形的夫琅禾费衍射,验证正多边形孔衍射特性,并对亮度不同的不规则小孔衍射特性进行分析.
1)f=2 m,λ=500 nm,三角孔边长 a=1 mm,光屏宽度h=6 mm的衍射如图5所示.在垂直于三角形的3条边的方向和3个角的方向上衍射现象均明显,但边方向衍射更为显著,距离中心越远,衍射现象越弱.三角形的中央光强最强(即图5的中央亮斑).
2)f=2 m,λ=500 nm,六边形孔边长 a=1 mm,光屏宽度h=6 mm时的衍射如图6所示.在垂直于六边形各边的方向衍射现象明显,产生明暗相间的条纹,距离中心越远,衍射现象越弱,中央的衍射光强最强.

图 5 f=2 m,λ=500 nm,a=1 mm三角形孔衍射图样

图6 f=2 m,λ=500 nm,a=1 mm六边形孔衍射图样
3)f=10 m,λ=500 nm,圆孔半径 R=1 mm,光屏宽度h=10 mm时的衍射如图7所示.圆心光强最强,产生明暗相间的圆环,距离中心越远,衍射现象越弱.在夫琅禾费衍射中,以第一暗环为范围的中央亮斑的光强占整个入射光束光强的84%,这个中央光斑称为艾里斑,由公式可得艾里斑的线半径为

由图7(a)可以看出艾里斑的线半径大致为3.6 mm,与理论计算的结果大致相符.

图7 f=10 m,λ=500 nm,R=1 mm圆形孔衍射图样
4)f=2 m,λ=500 nm,面积为1 mm2的衍射平面上不规则小孔,光屏宽度h=10 mm时的衍射现象如图8所示.在垂直于各边的方向上衍射现象明显,产生明暗相间的条纹,且距离中心越远,衍射现象越弱.

图8 f=2 m,λ=500 nm,面积为 1 mm2异形孔衍射图样
5)任意形状任意亮度的光源也能通过该程序得到衍射图像.如图 9所示,f=2 m,λ=500 nm,正方形边长a=1 mm(孔内不同地方亮度值不同),光屏宽度h=10 mm时的衍射图像中可以看出,最大光强在正方孔中央,亮度值不同衍射强弱不同.

图9 f=2 m,λ=500 nm,边长为1 mm不同亮度正方形孔衍射图样
3 结论
本文基于惠更斯-菲涅耳原理,用 Matlab进行模拟仿真任意形状任意亮度孔的衍射图像,得到以下结论:1)同一衍射孔,在改变衍射面与光屏的距离时得到不同的衍射图像.当中心半波带k为偶数时,中心光强减弱;k为奇数时,中心光强加强;k小于1时,一直处于加强状态.随着焦距慢慢增大,几何中心光强处于减弱状态的情况就越来越少,最后一直处于加强状态[13].整个过程可以看做菲涅耳衍射到夫琅禾费衍射的一个过渡[13].夫琅禾费衍射图像随着k值的减小,中央亮斑越来越大,其暗纹的光强也逐渐趋向于零.2)正多边形衍射图像成中心对称分布,每条边的垂直方向衍射现象明显,边数越多,光强增强的方向越密集,并且在各角的方位上衍射呈条带分布(正多边形的边数n为奇数时呈亮条带,n为偶数时呈暗条带)[5].可以推断出当边数趋向于无穷时,衍射图像为圆孔衍射的图像.且可以看出当正多边形的边数为奇数时,在垂直边方向上的衍射比角方向上的衍射更显著.3)在远场衍射时,任意形状任意亮度的小孔,中央光强最强,周围的衍射光强与小孔各个位置的亮度有关,且遵循随距离增大光强减弱的规律.
