一种端到端的多模式星载SAR模块化仿真方法

李 彤，张 帆，梁维斌，孙晓坤*，周勇胜

(1.北京化工大学 信息科学与技术学院，北京 100029；2.中国科学院空天信息创新研究院，北京 100094)

0 引言

为辅助星载合成孔径雷达(Synthetic Aperture Radar,SAR)关键技术攻关、系统优化设计和性能指标验证，通常会构建SAR仿真系统。随着星载SAR在工作模式、时空分辨率和通道数量等多方面取得了快速发展[1-3]，对星载SAR仿真手段也提出了更高的要求。

目前针对SAR仿真的研究已经开展很多，一类是对目标特性进行仿真，例如ZHANG等[4]设计了基于计算机图形学的SAR场景仿真方法，张锐等[5]构建全方位、全频带的目标散射系数实现复杂目标的散射特性模拟；一类是利用多GPU或网格计算[6-7]对SAR仿真进行加速，突破分布式目标回波仿真的计算瓶颈。此外，还对SAR系统进行了建模仿真，不仅包括回波模拟，同时还考虑硬件系统、传输链路、模糊区以及天线方向图等对回波数据的影响[8-10]。赵淑清等[11]设计了SARSIMS模拟器，集成了条带、扫描和聚束模式的回波仿真及成像方法，丁泽刚等[12]实现了基于DSP处理器的SAR回波模拟器，实现对自然场景回波数据的实时仿真。

分析现有星载SAR仿真方法，仍旧存在以下问题：① 考虑的实际误差因素少，不能较为全面地模拟实际SAR系统工作流程；② 多模式SAR仿真时，仿真结构复杂、可维护性差，当对仿真采用的公共几何模型进行更新改进时，各模式需要单独修改，代码冗余；③ 仿真模型间耦合度高，使得仿真系统的扩展性差，难以灵活地引入各种实际数据或者加入新增系统模型。

针对上述问题，本文设计了一种端到端的多模式星载SAR模块化仿真方法，主要包括：① 模拟实际星载SAR从信号发射到数据下传的全物理链路工作流程，模拟模糊区等实际误差因素的影响；② 设计了一种低冗余的多模式仿真方法，基于条带仿真内核，完成条带、扫描、滑聚和TOPS四个成像模式进行仿真，实现仿真代码的复用，结构简洁清晰且方便维护；③ 进行模块化设计，构建了由15个模块组成的星地一体化仿真框架，拓展了仿真系统的扩展性，能够灵活考虑高轨、地面干扰和链路衰减等因素影响。

1 多模式星载SAR仿真模型

回波数据仿真通过建立信号模型、卫星平台模型、地球模型以及目标模型即可实现，而端到端的全链路星载SAR仿真不仅包括回波数据模拟，同时还包括雷达载荷，即天线、卫星姿态和收发通道等状态的模拟、信号传播链路的仿真、由于天线旁瓣导致的模糊区的模拟以及雷达数据下传时进行星地数据格式转换等。图1描述了端到端星载SAR的工作流程及仿真组成，本文仿真路线将从雷达探测到回波接收再到数据格式化下传，模拟完整的多模式星载SAR系统工作过程。

图1 端到端星载SAR工作流程及仿真组成Fig.1 End-to-end spaceborne SAR workflow and simulation composition

1.1 条带模式星载SAR回波信号模型

回波模型采用由Wu等人[13]提出的适用于机载和星载SAR的信号模型，采用基于FFT的快速时频域仿真方法[14]，同时考虑仿真多种实际传播过程中的误差因素，信号模型为：

(Grc·exp(-jωrcτ))·Wa[θi]·LtmtLrmt·

(1)

式中，τ表示距离向快时间；t表示方位向慢时间；T表示方位向脉冲数量；M表示分布式目标点个数；σi·exp(jφi)为目标点i的散射特性；Gtc·exp(-jωtcτ),Grc·exp(-jωrcτ)分别为发射和接收通道的幅相特性；Wa[θi]表示天线方向图增益，其中θi为第i个目标点与波束中心之间的夹角；Ltmt和Lrmt分别表示收、发传输链路的对信号的衰减；ΔR(tn)表示链路对信号传播距离的影响；Ri(tn)为tn时刻卫星与目标点i的距离；λ为发射信号载频波长，与信号的工作频率有关；kr为线性调频信号调频斜率。

根据快速时频域仿真原理可以将上述表达式进行变换，即：

(2)

式中，

sr(τ)=(Gtc·exp(-jωtcτ))·(Grc·exp(-jωrcτ))·

exp(jπkrτ2)，

(3)

(4)

式中，回波信号可以看作两部分信号卷积结果。其中，sr(τ)表示距离向信号，它只与发射信号有关，而收发通道作为雷达载荷上信号发射和接收的终端，也直接影响发射信号；sa(tn,τ)表示方位向信号，该部分通过对卫星平台、地球模型、目标模型以及雷达载荷进行几何建模，精确计算目标点斜距，用于表示回波信号的相位。同时，方位向信号还包括传输链路部分，是由于传输链路直接影响目标斜距Ri(tn)。因此在后续系统仿真实现时，可将仿真流程按照该信号模型进行功能划分。

1.2 多模式星载SAR回波信号模型

由条带模式的回波信号模型可知，斜距R是计算回波相位、确定目标点位置的关键因素，而星载SAR扫描、滑聚、TOPS等模式的实现是基于波束的不同扫描方式，这使得各模式的斜距变化都不相同。斜距为：

R=f(θL,α)，

(5)

式中，θL和α分别表示雷达的入射角和斜视角，也代表了距离向和方位向2个维度，共同决定了天线的指向。扫描模式的子带划分通过改变入射角实现(文中将以3个子带为例)，滑聚、TOPS模式的方位向波束覆盖范围则通过控制斜视角实现。图2展示了不同模式的距离徙动曲线，滑聚和TOPS模式由于方位向斜视角的改变，相对于条带模式，初次探测到目标点时与目标点的距离更远，因此其距离徙动曲线更弯曲。

图2 各模式距离徙动曲线示意Fig.2 Schematic diagram of range migration curve of each mode

通过多模式星载SAR信号模型分析得出，除由于天线指向操作导致斜距的变化不同外，各个模式在卫星平台、目标平面、星地几何关系和误差引入等方面的模拟计算均相同，因此可以设计以天线指向为变量的多模式复用结构，通过控制θL和α实现多模式仿真。

1.3 多模式复用结构

仿真将采用适用于中低轨卫星仿真的“停-走-停”模型。卫星在“停”时完成收发信号过程，被认为是固定不动的，这其中也包括了天线的指向角度。因此，条带模式则可看作是天线指向相同的“停”时刻的集合；扫描、滑聚、TOPS模式则视为天线指向按规律变化的“停”时刻集合。

图3展示了4种成像模式的雷达入射角θL和斜视角α的分配方式。图中每个格子代表一个“停”时刻即一个方位向脉冲，根据各模式天线指向方式，赋予每个脉冲天线指向角度即可实现多模式仿真。其复用内核为一个走停结构。

图3 各模式入射角、斜视角的关系Fig.3 The relationship between the incident angle and oblique viewing angle in each mode

多模式仿真伪代码如下：

目前雷达的天线收发方式包括传统机械扫描、电子扫描等，不同的扫描方式实现的波束变化精度不同。对于机械扫描雷达，天线受机械驱动装置的控制，扫描存在一定时间间隔Δt。因此进行滑聚、TOPS等模式仿真时，波束角度变化步长只需要满足Nd=Δt·PRT≥1，则在Nd个驻留脉冲内天线角度视为相同，实现多个不同波束角度的驻留脉冲数为Nd的条带模式仿真。

对于电子扫描雷达，例如可实现连续扫描的相控阵雷达，其N0个阵元间波程差为N0dsinθ0，为了避免栅瓣效应，阵元间隔d<λ/(1+|sinθ0|)，因此该波程差一般小于距离门长度，可认为相控阵雷达在同一时刻的相位中心在一个距离门内，因此仿真可以简化为本文分解方法。以高分三号为例，其相控阵波束变化精度Δθ为0.01°，进行仿真时，选取的角度变化步长Nd、起止角度θstart与θend、驻留脉冲数量N与波束变化精度Δθ满足式(6)，本文分解方法可适用于相控阵雷达的回波数据仿真。

(6)

相比较于传统相互独立的仿真系统，实现结构复用的多模式SAR仿真系统具有结构简单、代码重用性高和便于维护等优势，如图4所示。

图4 传统仿真系统与复用仿真系统结构对比Fig.4 Structure comparison between traditional simulation system and reused simulation system

随着成像精度的提升，目标和卫星的轨道模型可能需要进行更替，传统仿真结构每个模式都需要进行替换和测试，而复用仿真结构只需修改复用结构中的模型，测试一次即可同步更新全部成像模式，大大提高了系统的使用效率。

2 复用结构模块化分解

复用结构使得系统的代码冗余度大大降低，但其内部的耦合度仍较高，不便于加入新增系统结构。为解决上述问题，本文将复用结构按功能进行模块化分解、封装，分解后的复用结构更加清晰，仿真模块间只有数据交互，对于未来可能新增的误差等模块，只需要根据误差原理修改相关模块的数据接口。

本仿真是建立在中低轨仿真模型基础上，对于高轨卫星，计算斜距需要考虑高度带来的时延问题[15-18]。在本文模块化仿真模型的基础上，增加高轨轨道六根数计算模块计算卫星的实时位置,增加接收斜距迭代模块进行时延误差的计算，即可实现高轨SAR回波数据的仿真，不需要对原有模块进行修改，这也体现了模块化仿真的优势。

2.1 模块介绍

各轨道模块化结构如图5所示。仿真结构按照功能需求分成了15个模块，这些模块根据1.1节信号模型中的距离向和方位向部分可划分为距离向、方位向以及数据处理三大部分。下面将对各个模块的具体功能进行介绍。

2.1.1 距离向部分

(1) 标准chirp信号模块

该模块产生标准的线性调频信号。

(2) 收发通道模块

该模块用于仿真收发通道的误差。在实际SAR系统中，信号的收发通道会受到系统内部信号模拟器件如滤波器、放大器等的影响，造成信号带内幅相特性误差[19]，对最终成像产生影响。通道幅相误差可看作是系统内各种误差因素的总和，以发射通道为例，Gtc(τ)为通道幅度误差，φtc=ωtcτ为通道相位误差，则经过发射通道后，信号I/Q通道信号为：

(7)

在实际仿真过程中，可为I/Q通道分别增加幅度不平衡误差δ和相位不平衡误差ε，以模拟通道不平衡。

(3) 回波信号接收长度计算模块

该模块属于信号采集模型，根据自定义回波采集窗口进行回波长度的计算。

(4) 距离向信号生成模块

该模块根据信号的接收长度将标准chirp信号进行长度补齐以及相位处理，得到距离向信号。同时，该模块还可注入内定标数据作为基准的发射信号进行仿真。

2.1.2 方位向部分

(1) 模糊区域解算模块

在实际星载SAR系统中，接收天线可能会接收到主观测区外模糊区的目标回波并存储，因此在利用主观测区参数成像时，模糊区回波成像参数失配，因此造成成像结果模糊[20]。模糊区包括距离向和方位向两部分。距离向模糊是由于收发信号重叠，而方位向模糊则是天线旁瓣增益导致，因此仿真过程中首先计算模糊区的多普勒频率及中心斜距，据此推算其对应的天线视角，进而根据天线方向图确定模糊区的回波增益。

(2) 星地坐标系转换模块

斜距计算采用了6个卫星空间坐标系[21]。式(8)展示了转动的地心坐标系Eg、不动的地心坐标系Eo、卫星轨道平面坐标系Ev、卫星平台坐标系Er、卫星星体坐标系Ee和天线坐标系Ea这6个坐标系之间的转换关系：

(8)

式中，Aog，Ago由仿真时间tn和地球转动速率ωe决定；Avo，Aov由轨道六要素中的轨道倾角、椭圆偏心率、升交点赤经决定；Arv,Avr由仿真时间tn以及轨道六要素中的椭圆半长轴、椭圆偏心率、过近心点时刻决定；Aer，Are由卫星的偏航角、俯仰角、横滚角决定；Aae，Aea由天线视角决定。

(3) 卫星轨道模块

卫星平台模块用于计算卫星轨道坐标并仿真卫星的轨道误差。根据开普勒第一定律和卫星轨道理论[22]，可通过6个轨道要素确定卫星在轨道上的位置(xvt,yvt,zvt)，并通过对坐标加减误差项实现轨道误差的加入，如式(9)所示。该模块可导入更为精确的卫星GPS实际坐标数据进行轨道仿真。

(9)

(4) 目标模块

目标模块用于计算目标点的坐标。仿真采用短半轴为6 356.78km、长半轴为6 378.16 km的椭球形地球模型来计算目标点在转动坐标系的坐标(xgt,ygt,zgt)。通过目标高程hDEM的加减，来修正目标高度位置带来的坐标误差。

(10)

(5) 传输链路模块

传输链路模块用于模拟链路过程中造成的误差。电磁波在传输过程中容易受到大气介质的影响，从而发生折射、反射和法拉第旋转等变化，该模块主要模拟了折射现象对于传播中的回波信号的影响[23]。

链路误差包括相位延迟和传输损耗两部分，相位延迟部分主要模拟对流层和电离层的折射现象造成的斜距误差ΔR，进而根据该斜距误差计算造成的相位延迟exp(j4π·ΔR(tn)/λ)；传输损耗主要模拟电离层、对流层和自由空间等对电磁波强度造成的损耗，即：

Lmt=LFSl·LRl·LAl·LTl·LLl·LCSFl，

(11)

式中，LFSl为自由空间损耗；LRl为降雨损耗；LAl为大气吸收损耗；LTl为对流层损耗；LLl为电离层损耗；LCSFl为云雾雪损耗。

(6) 目标点角度计算模块

该模块将根据卫星轨道坐标和目标点坐标进行目标点距离波束中心偏移角度的计算，该角度将用于判断目标点是否在成像范围内。

(7) 瞬时斜距计算模块

斜距计算模块计算目标与卫星的距离并加入卫星的姿态误差。该模块将目标坐标转换到以天线为原点的坐标系Ea中，以准确描述目标点位置。在根据式(8)进行坐标转换的过程中，需要卫星横滚角θroll、俯仰角θpitch、偏航角θyaw等姿态参数，通过θroll±Δθr，θpitch±Δθp，θyaw±Δθy实现误差角度加入。

(8) 成像区域判断模块

成像区域判断模块主要用于模拟卫星在飞行过程中的波束脚印，判断目标点是否在波束范围β内。根据目标点角度计算模块得到的距离向夹角θir和方位向夹角θia，当该目标点与波束中心的实际夹角θi满足式(12)时，根据天线方向图计算该目标点处的天线增益，即：

(12)

(9) 方位向信号生成模块

方位向信号生成模块主要用于计算回波信号的相位信息，将前置模块计算得到的各目标点的斜距数据、增益参数以及后向散射系数参数进行整合，得到当前仿真时刻的方位向信号仿真数据。

2.1.3 数据处理部分

(1) 回波数据计算模块

该模块将方位向信号与距离向信号进行耦合。在前置模块已经完成距离向信号和方位向信号数据的准备工作，该模块将两部分数据转换到频域相乘，得到当前时刻的回波数据。若仿真模糊区域，该模块还将完成主观测区域与模糊区域的回波数据的累积叠加功能。

(2) 数据量化压缩模块

量化压缩模块将生成的回波数据进行量化压缩处理，然后可进行数据下传。该模块采用分块自适应量化(Block Adaptive Quantization，BAQ)处理算法对前置回波数据进行量化压缩，以降低SAR的回波数据率。同时为回波数据添加格式化的数据头信息，该数据头信息中包括了SAR回波数据的参数、数据大小及格式等信息，这些信息可辅助该回波数据的后续处理，例如成像处理。经过量化压缩以及辅助数据添加后得到的回波数据即为标准的原始回波数据。

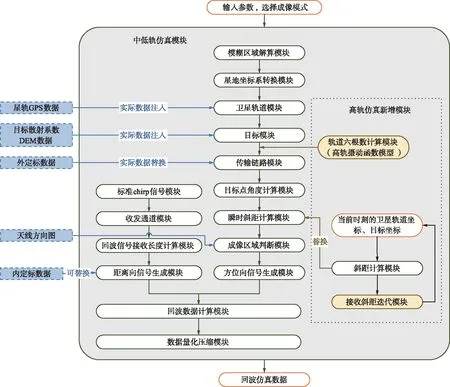
图5 各轨道模块化结构Fig.5 Modular structure diagram of each orbit

2.2 多模式SAR模块化仿真流程

多模式SAR回波仿真全流程如图6所示。首先，利用模糊区解算模块进行模糊区域的定位；其次，按照输入的仿真参数，调用各仿真模块实现条带仿真；最后，按照不同模式的入射角、斜视角调用条带模式的循环结构，完成多模式星载SAR仿真任务。

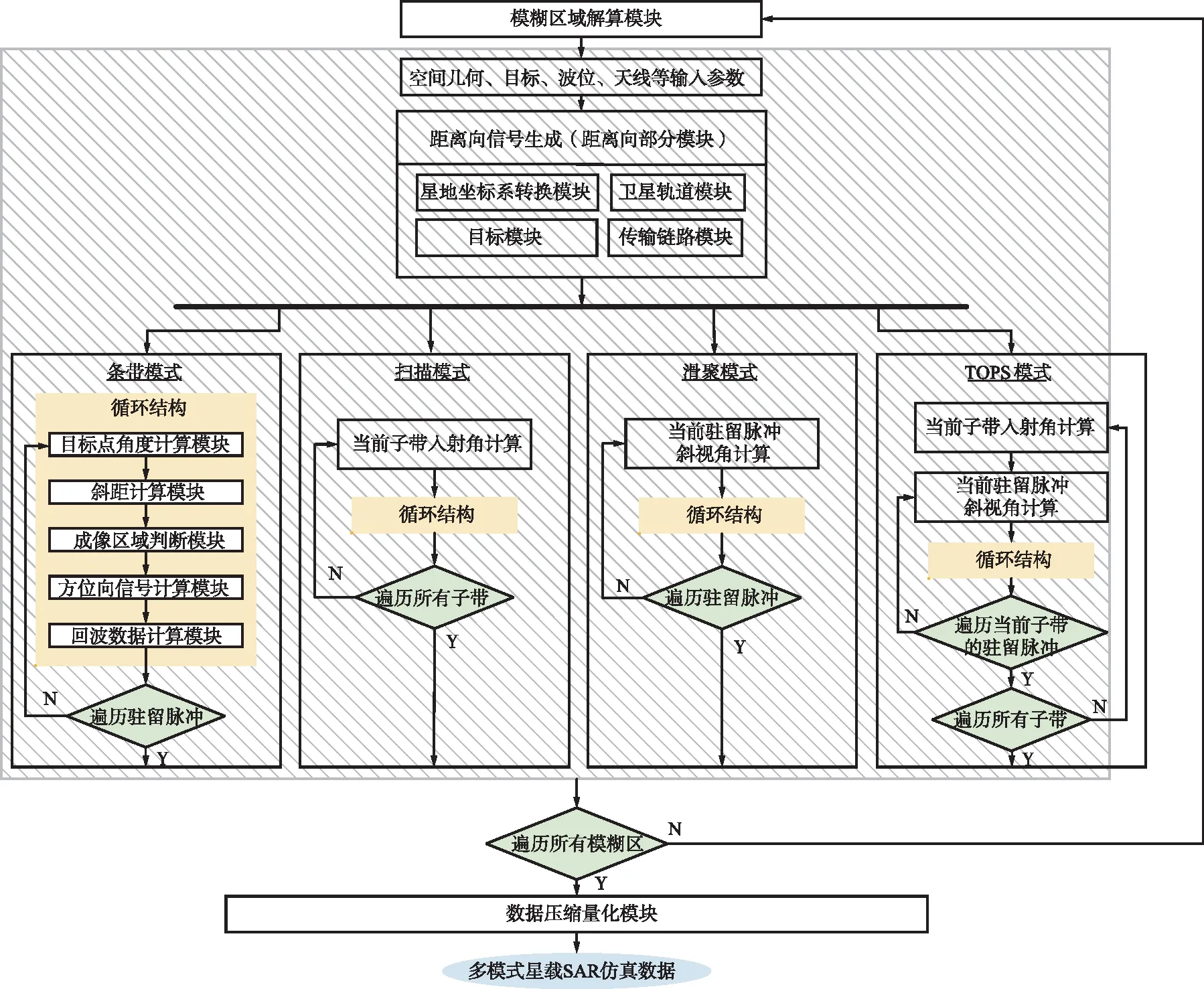
图6 多模式星载SAR仿真流程Fig.6 Flow chart of multi-mode spaceborne SAR simulation

3 系统仿真结果

3.1 理想回波仿真结果分析

为了验证仿真的可行性及正确性，对仿真数据进行成像并分析。实验仿真参数设置如表1所示，图7展示了条带模式和TOPS模式点目标成像结果，其中方位向和距离向采样点均为8 192。可以发现，经过成像系统处理后的点目标被较好地聚焦在场景中心。

表1 点目标仿真参数

(a) 条带模式

点目标的距离向和方位向脉冲响应如图8所示。在SAR成像过程中，线性调频信号经过脉冲压缩处理后，其峰值旁瓣比和积分旁瓣比理论值分别为-13，-10 dB左右。表2展示了点目标在距离向和方位向2个方向上的指标测试结果。结果表明，本文仿真系统模拟的原始数据是精确的。

(a) 条带模式

表2 条带和TOPS模式点目标成像理论指标

为了充分评估仿真系统的正确性，对分布式目标进行了仿真和数据分析。图9展示了分布式目标的仿真结果。

图9 分布式目标成像结果Fig.9 Imaging results of distributed targets

目标为1 000 pixel×1 000 pixel，经过回波数据模拟和成像处理后，裁剪出模拟区域的图像。结果表明,所设计分布式目标成像结果清晰,聚焦良好且完全还原模拟区域的状态。

3.2 加入误差后的回波仿真结果分析

在理想回波数据仿真结果的基础上，模拟分析收发通道、传输链路、姿轨误差、高程信息和模糊区等对回波仿真的影响。

3.2.1 收发通道误差

表3和图10展示了将仿真的通道幅相误差叠加到发射信号中得到的结果。结果表明，当前仿真的通道误差对信号的影响主要在距离向上，信号旁瓣上升，散焦严重。

表3 加入通道误差后的理论指标对比

(a) 距离向脉冲响应图

3.2.2 传输链路误差

由于SAR设备发射和接收信号的延迟时间在仿真中忽略不计，因此在链路仿真过程中也忽略了发射和接收之间的误差。表4给出了链路模块计算得到的点目标的相位延迟和幅度衰减；表5和图11给出了经过成像处理后的信号脉冲响应和与理想信号的指标对比结果；链路引起的相位误差由目标点的坐标体现，如表6所示。

表4 链路仿真结果

表5 加入链路误差后的理论指标对比

(a) 距离向脉冲响应图

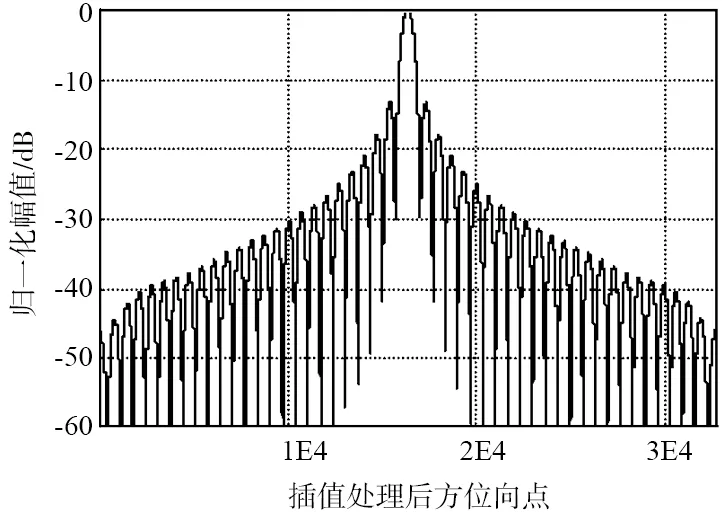
(b) 方位向脉冲响应图11 叠加链路误差的点目标距离向和方位向脉冲响应Fig.11 Range and azimuth impulse response diagram of point target after adding link error

表6 目标点的位置偏移

仿真结果表明，当前仿真目标点分辨率为5 m,发射信号为L波段，链路误差对信号的指标影响不明显，但会使得最终目标点定位出现误差。

3.2.3 高程及姿轨误差

除了链路和通道误差，还通过仿真系统分析了高程信息、姿轨误差对回波信号的影响。表6也展示了目标点高度设置为100 m的坐标变化，目标点的高度直接影响雷达探测到该点的时间，进而影响该点回波的相位，因此在二维成像图中会使得该目标点的位置在距离向上发生偏移。

表7展示了卫星横滚角误差设置为0.1°时场景中心斜距的变化值，卫星的姿轨误差主要影响天线的指向角度，使得波束中心的位置发生变化，由于仿真始终以波束中心为场景中心，因此该误差的影响最直观地体现在场景中心斜距大小上。

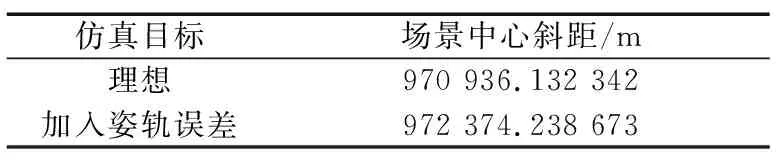
表7 姿轨误差对斜距的影响

3.2.4 模糊区仿真

按照模糊区与主观测区的多普勒频率以及中心斜距的差值，计算出各模糊区的天线视角并进行模糊区仿真以及天线方向图增益的确定，各仿真区的仿真参数如表8所示。

表8 各仿真区仿真参数

将模糊区与主观测区按模糊度的功率比进行回波数据的叠加，得到的成像结果如图12所示。

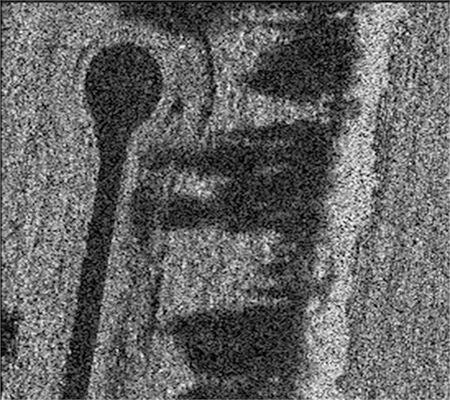
(a) 无模糊

其中,图12(a)为无模糊的主观测区仿真结果，图12(b)为叠加距离向与方位向模糊后的仿真结果，由于模糊区域的多普勒参数与场景中心斜距与主观测区不同，因此模糊区成像结果散焦，其次由于天线方向图限制，模糊区信号功率小于主观测区，模糊区的成像结果隐约可见。

3.3 考虑干扰源的SAR回波仿真结果

实际电磁环境复杂，雷达正常工作过程中可能会受到其他电子设备电磁信号的干扰[24]。在本文提出的多模式星载SAR仿真方法的基础上，可增加干扰叠加模块，进行复杂电磁环境的仿真和干扰信号的研究。干扰信号参数如表9所示。

表9 干扰信号参数

图13展示了加入表9所示干扰信号后的成像结果。

图13 考虑干扰源的成像结果Fig.13 Imaging results considering interference sources

相比于理想回波仿真，在模拟区域部分明显增加了多条长条状干扰。在成像时，由于干扰信号与回波信号的脉冲压缩参数并不匹配，导致干扰信号无法聚焦，成像结果表现为块状。同时，干扰源发射的信号为线性调频脉冲串，信号发射持续时间长，因此载荷在不同驻留脉冲内都可以接收到干扰信号，出现图中干扰块上下参差的现象。通过增加干扰模块实现，证明了本文所提出星载SAR仿真方法的可扩展性。

4 结束语

随着多维度、高轨星载SAR技术的发展，传统雷达系统的基础性技术支撑手段已经不再完全适用。本文提出了一种端到端的多模式星载SAR模块化仿真方法，实现从发射信号到数据下传全物理链路仿真；统一了4种成像模式的仿真结构以降低仿真系统的冗余度；并通过模块化使得仿真结构更为清晰，易于后期增删模块；同时仿真系统也为误差项提供数据交换接口，实现实际误差数据的交互。提出的仿真方法在未来的工作中有望应用于以天线指向为操作基础的新模式星载SAR系统，同时可以进行新功能的叠加交互操作。