基于Pansharp模型色彩高保真优化的高分遥感影像融合方法
2021-12-12常学立郭鑫轶
常学立,郭鑫轶,严 盟
(湖北工业大学 计算机学院,湖北 武汉430068)
0 引言
在遥感数据应用领域中,道路检测、水体提取、路径规划等多个方面的应用都要求图像既有高空间分辨率又兼有高光谱分辨率的特性,而遥感影像的空间分辨率与光谱分辨率是一对“矛盾”,若要获得高空间分辨率影像,则该影像的光谱信息保真度就不会很高;相反,若要获得高光谱分辨率影像,则该影像的空间信息融入度就不够。当前大多对地观测遥感卫星同时搭载全色载荷和多光谱载荷,其中全色载荷具有高空间分辨率的特点,多光谱载荷具有高光谱成像获取的能力,在后期数据处理中将全色载荷获得的高空间分辨率全色影像和多光谱载荷获得的高光谱分辨率多光谱影像进行融合,可以兼顾高空间分辨率与高光谱保真度的特点,从而提高遥感数据应用效能。
传统遥感影像融合算法中基于空间域的方法较多,基于空间域的遥感影像融合方法是直接在像素级别上进行运算,常用的算法有Pansharp算法[1]、IHS算法[2-3]、Brovey算法[4-5]和SFIM算法[6-7]等。Pansharp算法是根据全色影像与多光谱影像之间的关系,利用最小二乘法求出调制解调系数,该方法具有良好的空间信息保持度但存在局部光谱畸变的问题;Wei等[8]利用Pansharp模型的特性,将该融合算法巧妙地运用在医学图像处理方面,对PET/CT图像进行融合,达到了很好的效果;IHS算法是将影像从RGB色彩空间转换到IHS色彩空间,然后用全色影像替换I分量,逆变换到RGB空间,该方法同样存在光谱畸变的问题;王瀛等[9]将IHS、PCA、小波变换3种融合算法相结合,利用各个算法的优势,最大程度地减少替换成分相关性不高造成的光谱扭曲问题,取得了较好的融合效果;SFIM算法是将全色影像邻域滤波结果作为模拟全色影像,然后再根据融合模型进行融合,该方法存在空间信息融入度不足的问题;王密等[10]提出了一种自适应高斯滤波与SFIM模型相结合的全色多光谱影像融合方法,通过高斯滤波得到的模拟全色影像来替换邻域滤波得到的模拟全色影像,弥补了SFIM算法空间信息融入度不足的缺点;Brovey算法是一种将全色影像波段与低分辨率彩色影像各波段相乘得到融合影像的方法,该方法存在严重的光谱畸变;林志垒等[11]提出了一种改进的Brovey变换方法,针对传统Brovey变换融合存在的光谱信息丢失及光谱扭曲等问题,引入自适应加权平均对其进行改进,能有效地减少融合过程中光谱信息的损失和畸变。
通过以上阐述和分析,可以发现传统融合方法只能在光谱保真度或空间信息融入度中的某个方面有较好的效果,针对此现象,不同学者对传统融合算法进行了改进,使其兼顾高空间信息融入度与高光谱信息保真度的特点。本文也是从这个角度出发,提出了一种基于Pansharp模型,利用IHS变换计算模拟全色影像的遥感影像融合方法,通过IHS变换可提高图像的色彩保真度,解决了融合结果出现光谱畸变的问题,从而可以使图像在光谱保真度和空间信息融入度2个方面都有很好的表现,以下将对本文方法进行详细介绍。
1 基于Pansharp模型色彩高保真优化的高分遥感影像融合方法
1.1 Pansharp算法分析
Pansharp融合算法是基于最小二乘法对参与融合的原始多光谱影像、全色影像与融合后的多光谱影像、全色影像之间的灰度值关系进行最佳匹配的方法,是采用统计的方法来解决融合过程标准化和自动化问题的方法[12]。Pansharp模型为:
(1)
式中,x,y为图像像素的坐标点;FusedBandi为融合后图像的第i波段;Multii为多光谱图像的第i波段;PanOrig为原始的全色影像;PanSyn为全色影像和多光谱影像根据最小二乘法计算出的模拟全色影像,用于消除多光谱影像的空间信息以及全色影像的光谱信息。
Pansharp融合算法有很好的空间信息融入度,但计算出的模拟全色影像不足以消除全色影像的光谱信息,从而导致融合影像产生光谱畸变的问题,因此本文提出了一种可有效地消除全色影像光谱信息的方法,将新计算出的模拟全色影像代入Pansharp融合模型中,可以得到具有高空间分辨率与高光谱保真度的融合影像,解决了Pansharp算法导致的光谱畸变问题。
1.2 改进策略
Pansharp模型的特点在于:如果模拟全色影像具有与多光谱影像相似的空间分辨率,且具有与全色影像相似的光谱分辨率,则利用该模型计算出的融合影像将具有多光谱影像光谱信息以及全色影像空间信息的特点,因此在模拟全色影像计算方法上加以改进,使其在消除多光谱影像空间信息的同时还可进一步地消除全色影像的光谱信息是本文方法改进的重要方向。本文算法流程如图1所示。
首先以全色影像为参考影像,对同区域内的多光谱影像进行配准,使得两图中同一空间位置的点对应起来;然后将多光谱影像通过IHS正变换计算出的I分量归一化得到模拟全色影像,用于消除多光谱影像的空间信息以及全色影像的光谱信息;最后依照Pansharp模型对全色影像、多光谱影像以及计算出的模拟全色影像进行融合即可获得高分辨率多光谱影像。
1.3 本文方法
1.3.1 影像配准
对遥感影像进行配准,主要目的是将不同时间、不同视角或不同传感器下捕获到的相同场景中的2幅或多幅影像(参考影像和待配准影像)对准到共同空间轴[13]。在遥感领域,全色载荷获取的影像相较于多光谱载荷获取的影像有着较高的空间分辨率,并且由于传感器以及视点的不同导致获取的影像存在点对点之间的差异,如果不进行配准,则全色影像与多光谱影像在相同坐标空间下信息的不一致会导致融合影像融合了不同坐标下的空间信息,因此在影像融合前需要进行影像配准,使得全色影像与多光谱影像对应于空间同一位置的点一一对应起来,从而达到增强信息融合的目的。本文采用SIFT[14-15]算法以全色影像为参考影像对多光谱影像进行配准,首先利用双线性插值算法对多光谱影像上采样,使其具有与全色影像相同的空间分辨率;然后通过特征点提取与特征点匹配确定图像变换模型;最后根据图像变换模型对图像进行变换插值计算出配准后的多光谱影像。整体流程如图2所示。
1.3.2 模拟全色影像计算
在实际条件下,Pansharp模型很难获得理想的模拟全色影像,导致多光谱影像与全色影像的融合结果存在光谱畸变的问题。本文提出的新模拟全色影像计算方法可极大程度上避免融合影像光谱信息丢失,达到色彩高保真的效果。
IHS变换用全色影像作为新的I分量替换IHS坐标系下原始I分量,然后再逆变换至RGB坐标系中得到融合影像,该方法具有良好的空间信息融入度。只替换I分量就可以使影像融入全色影像的空间信息,由此可见,I分量可以用来表示全色影像的空间信息,因此本文采用IHS正变换获得模拟全色影像以此提高融合影像的光谱保真度。模拟全色影像计算步骤如下:
① 取得以全色影像为参考影像配准后的多光谱影像。
② 对配准后的多光谱影像进行正变换获取I分量,计算公式如式(2)所示,其中R,G,B分别为3个通道的像素值组成的向量,I为IHS坐标系下I分量组成的向量,V1,V2为中间变量:
(2)
③ 利用式(3)对I分量进行归一化,计算出模拟全色影像Inew,其中gray为目标图像的最大灰度值,Imax,Imin分别为原I分量中的最大最小值,此时,模拟全色影像就有着与原始多光谱影像相似的空间分辨率和全色影像相似的光谱分辨率:
(3)
根据上述步骤计算出模拟全色影像,如图3所示。
由图3可以看出,一方面,模拟全色影像的空间分辨率明显低于全色影像的空间分辨率且与多光谱影像的空间分辨率基本相同;另一方面,模拟全色影像的光谱分辨率与全色影像保持一致。因此本文方法获得的模拟全色影像非常适合Pansharp模型,它可以很好地消除多光谱影像空间分辨率和全色影像光谱分辨率,让融合影像能够兼顾高空间分辨率和高光谱保真度的特性。

(a) 原始多光谱影像
1.3.3 影像融合
影像融合是按一定规则将多光谱影像和全色影像进行融合从而获得高空间分辨率多光谱影像的过程。本文采用的是Pansharp融合模型,该模型主要利用模拟全色影像保留全色影像的空间信息以及多光谱影像的光谱信息,以此获得高空间分辨率和高光谱保真度的融合影像。在上述步骤中已经计算获得了配准后的多光谱影像以及全色影像,并且根据本文方法计算出了新模拟全色影像,因此通过式(4)即可计算融合影像每个波段的像素值,最终按照多光谱影像波段的排列顺序对每个波段的计算结果进行组合即可得到融合影像:
(4)
式(4)在式(1)的基础上替换了模拟全色影像的计算方法,其中x,y为图像像素的坐标点;i表示当前为第i波段;FusedBandi为融合后影像的第i波段;Multi为配准后的多光谱影像;Panorig为原始全色影像;PanSyn_new为本文方法计算出的新模拟全色影像。
2 实验结果与分析
2.1 实验数据
本文采用高分辨率多模成像卫星(高分多模卫星)数据作为实验验证数据,高分多模卫星是《国家民用空间基础设施中长期发展规划(2015—2025年)》中分辨率最高的光学遥感卫星,也是我国第一颗优于0.5 m分辨率敏捷智能遥感卫星,该卫星搭载了1台分辨率全色0.5 m/多光谱2 m的高分辨率光学相机。高分多模卫星传感器参数如表1所示。
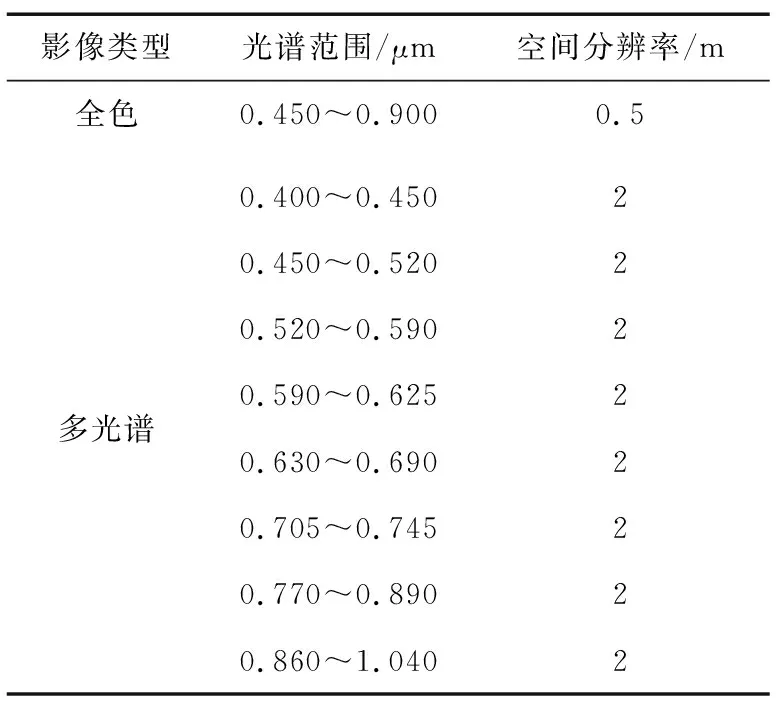
表1 高分多模卫星传感器参数
2.2 算法比较与分析
本文方法在Pansharp算法以及IHS算法的基础上提出改进策略,为了证明该方法的有效性,实验选取Pansharp算法、IHS算法与本文方法进行比较,地物为山时不同融合方法与本文融合方法融合效果的对比结果如图4所示,地物为房屋时的不同融合方法与本文融合方法融合效果的对比结果如图5所示。

(a) 原始多光谱影像

(a) 原始多光谱影像
图像融合质量评价包括空间质量、多光谱图像色彩保真度2个方面,评价方法分为主观评价和客观评价[16-17]两大类。从主观上看,3种算法的融合效果与原始多光谱影像相比空间分辨率均得到了改善,提高了影像轮廓信息并且保留了影像的光谱特性。客观上选取6个评价指标对融合结果进行质量评价,分别是平均梯度(Average Gradient,AG)、相关系数(Correlation Coefficient,CC)、信息熵(Information Entropy,IE)、光谱保真度指数(Spectral Fidelity,SF)、结构相似性指数(Structure Similarity,SS)以及通用像质计(Universal Image Quality Indicator,UIQI)[18-19]。平均梯度可以反映图像的清晰度,平均梯度越大影像越清晰;相关系数反映2幅影像之间光谱特征的相似程度,相关系数越高,光谱的保真度越高,相关系数的理想值为1;信息熵是一种基于信息量的评价指标,信息熵值越大,表明影像携带的信息量越大,影像轮廓越清晰;光谱保真度指数是一种基于光谱信息保真度的评价指标,光谱保真度越大说明影像的光谱信息保持的越好;结构相似性指数是指融合后的影像与原始多光谱影像的相似度,指数越大,相似性越高;通用像质计是对影像综合质量的评价,指数越大表明影像融合效果越好。针对不同融合算法的评价指标如表2和表3所示,表2对应图4中的融合结果,表3对应图5中的融合结果。

表2 地物为山时不同融合算法质量评价表

表3 地物为房屋时不同融合算法质量评价表
平均梯度和信息熵可以很好地表示空间信息的融入度。就平均梯度而言,Pansharp融合算法的平均梯度不管地物是山还是房屋时都处于最高位置,效果最好,本文方法次之,效果居中;就信息熵而言,在地物为山时,本文方法信息熵最大,比Pansharp融合算法稍高,效果最好,IHS算法效果较好。因此Pansharp算法和本文算法的空间信息融入度最高,效果最好,而在地物为房屋时,Pansharp融合算法的信息熵最高,效果最好,本文方法与IHS算法相差不大,效果居中。
相关系数和光谱保真度指数可以很好地表示光谱信息的保真度。就相关系数而言,各种算法相差不大;就光谱保真度指数而言,地物为山时,本文方法效果最好,Pansharp算法居中,IHS算法效果较差,地物为房屋时,IHS算法效果最好、本文算法效果居中,Pansharp算法效果最差。
结构相似性指数可以用来表示融合结果与原始多光谱影像结构之间的相似度,通用像质计可以用来评价融合影像的总体质量。地物为山时,结构相似性指数和通用像质计表现为相同的结果,IHS算法效果最好,本文算法效果居中,Pansharp算法效果最差,而地物为房屋时,本文方法效果最好,Pansharp算法效果居中,IHS算法效果最差。
2.3 实验结论
本文对IHS正变换获得的I分量进行归一化处理来获得模拟全色影像;然后根据Pansharp模型特性将得到的模拟全色影像代入求得融合影像。不论从主观还是客观评价2个方面都可以看到本文方法在多个方面表现出的融合效果都要优于传统融合算法,能够很好地解决IHS算法和Pansharp算法出现的光谱畸变问题,并合理利用Pansharp模型的特性,在保证融合结果有良好光谱信息保真度的同时还能够融入全色影像的空间信息,得到具有高空间分辨率和高光谱分辨率的融合影像。
3 结束语
本文首先介绍了Pansharp算法基本原理,指出了Pansharp算法计算出的模拟全色影像不足以消除全色影像光谱信息导致的光谱畸变问题,并就如何提高光谱保真度来解决光谱畸变的问题提出了改进方向。然后,提出了一种基于Pansharp模型的改进高分遥感影像融合方法,该方法通过利用IHS变换计算新的模拟全色影像,达到了提高融合图像色彩高保真度的目的,优化了空间信息融入度不够与光谱畸变的问题。最后,通过高分多模卫星全色和多光谱影像数据对本文方法进行了实验验证,并从主观和客观2个方面对融合结果进行了评价,实验结果表明本文方法除了在色彩保真度方面具有较好的效果外,还能很好地融入全色影像的空间信息,达到了较好的融合效果。
