温度对玻璃纤维/环氧复合材料吸湿扩散行为的影响
2021-12-12朱礼宝李永清
朱礼宝,李永清,朱 锡
(海军工程大学 舰船与海洋学院, 武汉 430033)
纤维增强树脂基复合材料具有高比强度、比刚度,物理化学性能优异和设计性良好等特点,广泛应用于航空航天、交通运输、土木工程和海洋工程等领域。复合材料结构件在使用过程中可能会暴露于水、海水、混酸[1]等介质,导致其性能下降,研究介质在复合材料中的扩散是预测复合材料耐久性的首要任务。
实际服役情况下,介质会从多个方向进入复合材料,因而需要考虑介质在复合材料不同方向的扩散性能。树脂封边[2-3]是获取材料各向扩散系数的一种方法,但存在树脂脱落及密封性的问题。Arnold等[4]依据大量吸湿实验结果,对比了单向碳纤维/环氧复合材料板三维扩散系数的获取方法,结果表明,采用三维扩散公式获取复合材料扩散系数精度最高,且垂直于纤维的两个方向的扩散系数不相同。Jiang等[5]采用三维扩散公式及有限元模拟方法研究了玻璃纤维增强复合材料的扩散系数。近年来,研究人员[6-7]在三维扩散系数的基础上,结合复合材料微观结构和有限元法,对复合材料吸湿扩散影响因素进行了研究。
温度是影响复合材料吸湿扩散行为一个重要因素。Bond[8]认为,材料的扩散系数通常由温度决定,饱和吸湿量通常由环境介质浓度决定。Xin等[9]开展了拉挤复合材料在不同温度下的吸湿实验,回丽等[10]开展了碳纤维/双马复合材料在不同温度下的吸湿实验,并依据实验结果建立了考虑温度的复合材料吸湿动力模型。然而,这些研究均未考虑复合材料吸湿扩散的方向性,且吸湿温度均低于玻璃化转变温度,无法判断温度对各向扩散系数的影响程度。
本工作在上述研究的基础上,通过设计试样形状和温度梯度,开展单向玻璃纤维/环氧复合材料在不同温度下的吸湿实验,探究温度在低于和高于饱和吸湿复合材料玻璃化转变温度时对其三维吸湿扩散行为的影响及机制。
1 吸湿扩散理论
水进入复合材料属于水浓度梯度驱动的扩散过程,可用Fick模型的瞬态扩散过程进行描述。对于板状材料,其一维和三维吸湿表达式分别如式(1)和式(2)所示[11]:
式中:C为水分浓度,mol•m−3;D为扩散系数,m2•s−1;x为沿扩散方向的坐标。恒温恒湿条件下一般假设D为定值。
设Wt为t时刻复合材料的吸湿百分量(简称吸湿量),W∞为饱和吸湿量(即达到吸湿平衡时的吸湿量),材料初始为干燥状态,可得一维和三维吸湿状态下吸湿量与时间的关系如式(3)和式(4)所示:
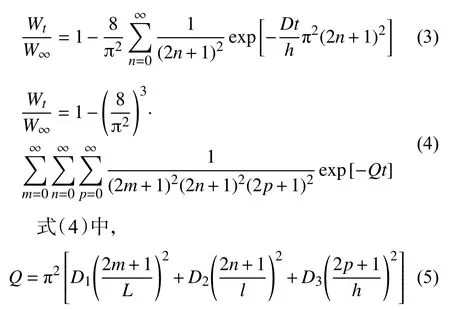
式中:L、l、h为沿扩散方向的材料尺寸。
水扩散进入复合材料,宏观表象为吸湿量的增加。在复合材料内部,水吸收会造成树脂基体的膨胀,同时,树脂开始出现如水解、分子链断裂、小分子物质生成并逸出等物理/化学降解现象。这些降解过程在低温、短时间内表现不明显,但在高温、长时间环境下会加剧,与Fick吸湿增重过程叠加后,吸湿曲线会呈现non-Fick状态。当物理/化学降解造成的质量损失大于水分吸收时,复合材料吸湿量降低,这一降解过程称为松弛吸湿过程。因而在高温环境下,复合材料的吸水过程除Fick扩散外,还包含松弛过程[9,12],Fick-松弛耦合模型表达式为:
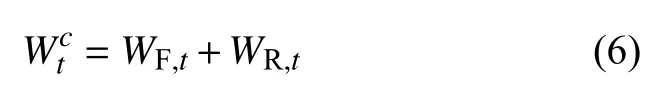
式中:WF,t、WR,t分别是t时刻Fick扩散主导的吸湿量(由式(3)、式(4)获得)和松弛主导的吸湿量。对于松弛吸湿过程,考虑多重黏弹性过程,其一般表达式为::
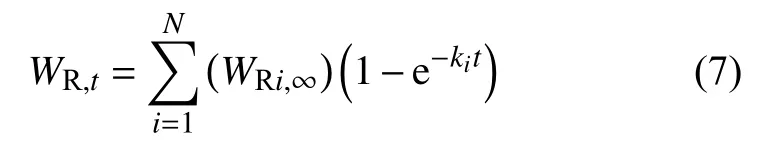
式中:k是松弛率常数;WRi,∞是不同松弛过程的吸湿平衡量。本工作在计算中只考虑一个松弛过程,即i=1,其精度可满足要求。
2 实验材料与方法
2.1 实验材料
单向S玻纤/环氧复合材料由咸宁海威复合材料有限公司生产。单向S玻纤布型号SWU414,玻纤密度为2.54 g/cm3。纬向热熔纱起固定作用,线密度12 TEX,1.6根/cm。基体树脂采用环氧树脂-1001,固化剂为改性聚醚胺固化剂。采用真空成型法制备单向铺层的复合材料板,共7层,成型后板厚2.52 mm,单层厚度0.36 mm。
为获得复合材料的三维扩散系数,通过数控加工中心,沿单向铺层复合材料板的三个方向切割出10 mm×10 mm×1.5 mm的吸湿试样。定义沿单向铺层复合材料板的纤维方向为F方向,垂直于纤维且沿纬纱的方向为S方向,厚度方向为T方向。如图1所示,分别标记这三个方向的吸湿试样为F、S和T试样。最后用600#的砂纸打磨吸湿试样,以保证试样边缘平整,无毛刺。
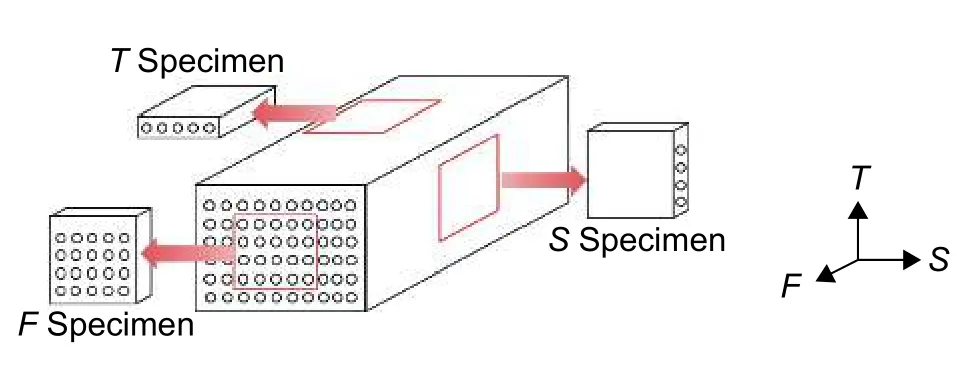
图1 复合材料试样示意图Fig. 1 Schematic diagram of composite specimen
2.2 实验方法
参考标准ASTM D3171,采用烧蚀法测定单向玻纤/环氧复合材料的纤维体积分数为46.7%,质量分数为65.7%。对于热熔纱,根据其线密度和分布密度计算得到质量分数约为0.3%,体积分数约为0.6%。
采用称重法测定复合材料的吸湿性能。参考标准ASTM D5229,首先将复合材料和树脂浇注体吸湿试样置于50 ℃烘箱中去除初始水分,直至试样质量不再变化。将复合材料的吸湿温度定为35 ℃、50 ℃、70 ℃,以对比不同温度对吸湿系数的影响。采用去离子水浸泡,每组重复3个试样。定期取出试样进行称重,分析天平精度为0.1 mg,称重前将试样表面水分充分吸干。吸湿量采用式(8)计算:

式中:Mt和Mo分别为t时刻和初始时刻的试样质量。
为分析吸湿对复合材料玻璃化转变温度的影响,制作尺寸为40 mm×4 mm×2 mm的DMA试样,其中试样长度方向为沿纤维方向,宽度、厚度方向分别沿图1中S方向和T方向。采用METTLER TOLEDO DMA1型动态力学热分析仪对在不同温度下饱和吸湿的DMA试样进行测试,测试模式为三点弯曲,扫描温度35 ~120 ℃。为探究复合材料在吸湿过程中是否发生化学变化,采用Bruker TENSOR Ⅱ型红外测试仪对饱和吸湿后的试样进行扫描。
3 结果及讨论
3.1 吸湿实验结果
3.1.1 35 ℃及50 ℃吸湿实验结果
图2(a)~(c)分别为35 ℃时复合材料试样F、S和T方向的吸湿实验结果,图(d)~(f)分别为50 ℃时复合材料试样F、S和T方向的吸湿实验结果。可以看出,复合材料的吸湿量随时间1/2次方先线性增加,后趋于水平,符合Fick过程。采用Fick一维扩散公式和三维扩散公式对实验数据进行拟合,得到结果如图2“Fick-1D”、“Fick-3D”和表1所示。可以看出,35 ℃时,复合材料的饱和吸湿量在1.11%~1.16%之间;50 ℃时,复合材料的饱和吸湿量在1.16%~1.21%之间,两个温度下的饱和吸湿含量相差不大。而温度升高增强了水的活性,使得复合材料在50 ℃吸湿时扩散系数增大。对于复合材料的三维扩散系数,F方向扩散系数最大,因为该方向没有纤维阻碍,且纤维/基体界面会加速吸湿过程;垂直于纤维的S方向和T方向扩散系数均小于沿纤维方向,说明纤维对吸湿过程的阻碍作用明显,而由于纬纱及层间的存在使得S方向扩散系数大于T方向扩散系数,这与Arnold[4]的实验结果一致。

表1 35 ℃和50 ℃时复合材料吸湿扩散系数及饱和吸湿量Table 1 Hygroscopic diffusivity and saturation moisture content of composite at temperature 35 ℃ and 50 ℃
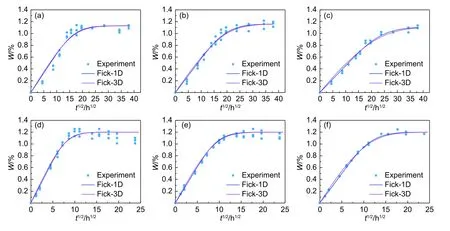
图2 35 ℃及50 ℃时吸湿实验及Fick模型拟合结果对比图 (a)35 ℃,F试样;(b)35 ℃,S试样;(c)35 ℃,T试样;(d)50℃,F试样;(e)50 ℃,S试样;(f)50 ℃,T试样Fig. 2 Comparison between experimental data and Fick model fitting curves at temperature 35 ℃ and 50 ℃ (a)35 ℃,F specimen;(b)35 ℃,S specimen;(c)35 ℃,T specimen;(d)50 ℃,F specimen;(e)50 ℃,S specimen;(f)50 ℃,T specimen
3.1.2 70 ℃吸湿实验结果
图3(a)~(c)分别为70 ℃时复合材料F、S、T试样的吸湿实验结果。初始阶段复合材料吸湿量随时间1/2次方线性增加,符合Fick扩散模型,但在达到最高点后逐渐下降,偏离Fick模型。将复合材料吸湿量的平均峰值作为饱和吸湿量,则饱和吸湿量在1.03%~1.06%之间,明显低于35 ℃和50 ℃时复合材料的吸湿量,说明高温环境下复合材料发生了质量损失。采用Fick一维扩散公式和三维扩散公式对实验结果进行拟合,得到结果如图3“Fick-1D”、“Fick-3D”和表2所示,Fick模型能描述吸湿量上升阶段,但与后续质量损失阶段相差较远。

表2 70 ℃时复合材料Fick模型吸湿扩散系数及饱和吸湿量Table 2 Hygroscopic diffusivity and saturation moisture content of composite at temperature 70 ℃ by Fick model
70 ℃吸湿环境下复合材料出现质量损失,说明复合材料在吸湿过程中发生了松弛现象。采用式(6)对复合材料吸湿过程进行拟合,得到结果如图3“Fick-Relax”。由图3可见, Fick-松弛耦合模型能较好地描述复合材料在高温下的吸湿行为。采用式(6)拟合得到参数如表3所示,其中Fick模型采用3D模型。

表3 70 ℃时复合材料Fick-松弛耦合模型吸湿扩散系数及饱和吸湿量Table 3 Hygroscopic diffusivity and saturation moisture content of composite at temperature 70 ℃ by Fick-relaxation coupled model
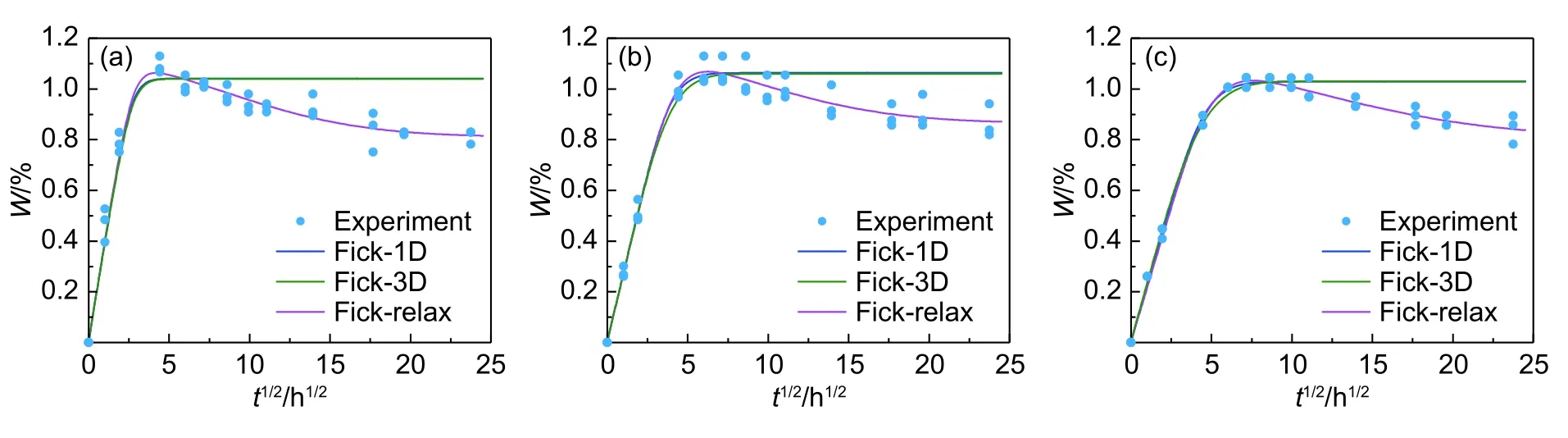
图3 70 ℃时吸湿实验及模型拟合结果对比图 (a)F试样;(b)S试样;(c)T试样Fig. 3 Comparison between hygroscopic experimental data and model fitting curves at temperature 70 ℃ (a)F specimen;(b)S specimen;(c) T specimen
3.2 DMA及FTIR测试结果
图4为干燥状态和不同吸湿温度下饱和吸湿状态复合材料的储能模量和损耗模量温度谱,玻璃化转变温度Tg取损耗模量达到峰值时的温度。由图4可以看出,水分吸收使得材料的储能模量和玻璃化转变温度降低,干燥状态复合材料的Tg为82.25 ℃,而35 ℃、50 ℃和70 ℃温度下饱和吸湿复合材料的Tg分别为64.45 ℃、67.15 ℃和67.54 ℃,下降明显,这是水分吸收引起的增塑所致。70 ℃时实验温度超过了饱和吸湿试样的Tg,复合材料在高温作用下可能会发生降解、物理老化,体现在70 ℃时饱和吸湿试样的储能模量最低,而Tg偏高[13]。
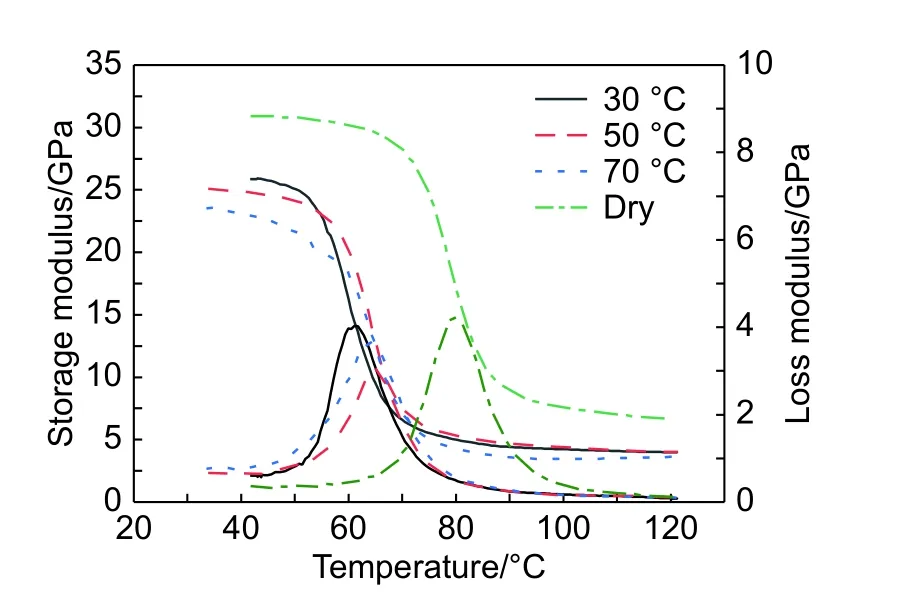
图4 干燥和不同温度下饱和吸湿复合材料的储能模量和损耗模量Fig. 4 Storage modules and loss modules for dry and saturated hygroscopic composites at different temperatures
图5为干燥状态和不同吸湿温度下饱和吸湿复合材料的FTIR图谱。由图5可看出,复合材料吸收峰位置基本不变,峰强度发生变化。初始干燥试样和35 ℃、50 ℃饱和吸湿试样在1035~1250 cm−1(C—O—C)、2870~2930 cm−1(—CH2—)和2965 cm−1(—CH3)的吸收峰强度基本不变,而70 ℃饱和吸湿试样的吸收峰强度减弱,说明环氧树脂在高温作用下发生了降解。复合材料在高温下的降解会使得其质量损失,表现为吸湿量减小,这与3.1.2节中70 ℃时的吸湿实验结果一致。
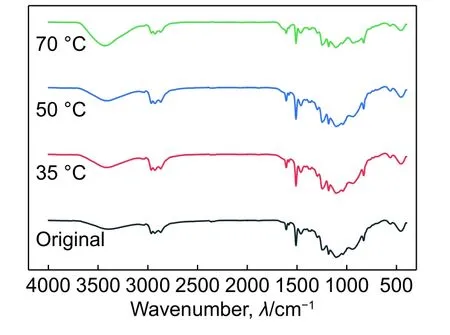
图5 初始和不同温度下饱和吸湿复合材料的红外图谱Fig. 5 FTIR for dry and saturated hygroscopic composites under different temperatures
3.3 温度对三维扩散系数的影响
考虑温度对复合材料三维扩散系数的影响,同时探究不同方向扩散系数之间的关系。分别将35 ℃和T方向扩散系数作为基准,计算扩散系数与各基准的比值,得到结果如图6所示。图6(a)以35 ℃下三个方向的扩散系数为基准,考虑温度对扩散系数的影响,可以看出,除70 ℃时F方向外,其余条件下的扩散系数比值基本重合。图6(b)以三个温度下T方向扩散系数为基准,考虑方向对扩散系数的影响,同样可以看出,除70 ℃时F方向外,其余条件下的扩散系数比值基本重合。上述结果表明,70℃下,复合材料在F方向上的水分吸收机理与其他条件下的水分吸收机理差异最大。结合前述扩散-松弛耦合水分吸收现象可知,高温环境(70 ℃)可能导致复合材料三个方向的水分吸收机理都发生了变化,但对F方向的影响最大。对于纤维增强树脂基复合材料,基体和纤维/基体界面都是复合材料吸收水分的重要通道,根据上述实验结果,可以分析高温环境不仅使得基体出现松弛过程,还导致界面沿F方向的扩散系数急剧增加,其增幅远大于S方向和T方向。

图6 温度和方向对复合材料扩散系数的影响 (a)温度;(b)方向Fig. 6 Effects of temperature and direction on composite diffusivities (a) temperature;(b) direction
研究认为[8-9],不同温度下复合材料的扩散系数符合Arrhenius方程:

式中:G为渗透指数,mm2•h−1;E为扩散过程的活化能,kJ• mol−1,R= 8.314 J•K−1•mol−1为气体常数;T为开尔文温度。对于同一种材料,其活化能E保持不变。
对式(9)取自然对数,得到对数扩散系数与温度倒数的关系如图7所示。由图7可以看出,ln(DF-70)偏移较大。拟合S方向和T方向数据,计算得到复合材料的活化能为78.15 kJ• mol−1。对于F方向,当温度低于50 ℃时,其活化能同样为78.15 kJ• mol−1。

图7 扩散系数对数与温度倒数的关系图Fig. 7 Natural logarithm of Fick diffusion diffusivities as function of inverse temperature
采用上述活化能和式(9)对S方向和T方向的扩散系数进行拟合,得到结果如图8所示,拟合值与实验值吻合较好。对于复合材料F方向,其在70 ℃时扩散机制发生变化,不能将其扩散系数与30 ℃和50 ℃时的数据进行拟合。由于数据拟合至少需要三个数据点,而从图6可知,温度在50 ℃以下时扩散系数比值基本相等,因而取温度为315 K(41.85 ℃),通过S方向和T方向的Arrhenius方程及比值关系计算出DF-41.85=2.45×10−3mm2•h−1,再拟合得到F方向的Arrhenius表达式。图8中,DF(Fit)仅在50 ℃及以下时可用,因而拟合结果远偏离DF-70的实验值。Arrhenius方程的渗透指数和活化能拟合结果如表4所示。
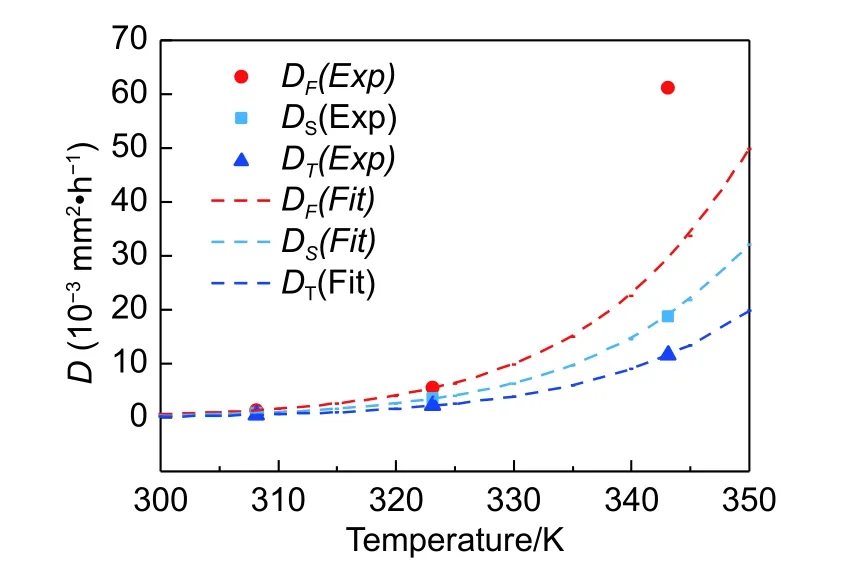
图8 吸湿扩散系数实验值与拟合值比较Fig. 8 Comparison between test results and theoretical fitting curves at different temperatures

表4 复合材料不同方向上的渗透指数和活化能Table 4 Permeability index and activation energy of the composite in different directions
4 结论
(1)吸湿温度高于饱和吸湿复合材料的玻璃化转变温度时,复合材料会出现降解和物理老化,导致质量损失,Fick-松弛耦合模型能较好地描述其吸湿行为。
(2)在30~70 ℃的温度范围内,复合材料垂直于纤维方向的扩散系数满足Arrhenius方程,活化能为78.15 kJ•K−1•mol−1,可用于预测不高于70 ℃时的吸湿扩散系数。
(3)高温对复合材料的界面影响较大,吸湿温度高于饱和吸湿复合材料的玻璃化转变温度时,界面沿纤维方向扩散系数的增幅大于垂直于纤维方向,其机理有待进一步探究。
