某大跨度挑台舒适度分析及振动控制

2021-12-10杨姝姮赵仕兴

建筑结构 2021年22期

杨姝姮，赵仕兴，周磊

(1 四川省建筑设计研究院有限公司，成都 610017；2 四川省建筑设计研究院有限公司复杂结构设计研究中心，成都 610017)

0 引言

近年来，山区景点陆续出现不少大跨度柔性悬挑钢结构，如重庆市云阳县龙缸悬挑玻璃景观廊桥、北京石林峡景区玻璃观景台[1]等。这类结构具有轻、柔、大跨度等特征，刚度小、基频低、阻尼小，容易受外部激励(人群荷载、风荷载等)而产生振动，引起使用者的不安和心理恐慌，从而降低建筑物的使用性能和舒适性，甚至引起破坏。因此对该类结构进行安全性及振动控制的研究显得尤为重要。本文针对某景观挑台，分别对其进行人行荷载、风荷载作用下的楼盖结构舒适度及振动控制分析，并开展人行荷载、风荷载共同作用下的楼盖结构舒适度研究工作。

1 工程概况

某景观挑台拟建于某山地近最高点处，海拔1 042.7m，距下侧湖面约173m。结构由椭圆环形玻璃走道、矩形直线玻璃走道和桁架拱组成，并设置预应力钢拉索，悬挑长度约27m，为大悬挑柔性钢结构。椭圆走道长轴约30m，短轴约20m，走道宽约3m，矩形走道长约18.7m，宽约3.5m，拱高约19m，结构效果图及布置图如图1所示。

图1 挑台结构效果图及布置图

2 结构在人行荷载作用下的振动特性

2.1 人行荷载的确定

人行荷载有别于车辆、风荷载、地震等作用，是一种动态荷载且具有明显的周期性。关于人行荷载的研究，往往是在基于大量试验数据的基础上进行统计分析。人行激励荷载模型包括单人荷载模型和人群荷载模型。国内外对单人荷载模型的研究较多，目前建立的各种各样的单人荷载数学模型主要可分为两类：确定性模型和随机性模型，其中确定性模型较简单、实用，主要采用傅里叶级数模型来近似表达，因而应用较多。

根据《建筑楼盖结构振动舒适度技术标准》(JGJ/T 441—2019)[2]，对建筑楼盖进行舒适度计算时可考虑单人行走激励和人群荷载，单人步行激励曲线采用傅里叶级数荷载模型，即：

直接测量人群产生的步行力不易实现，实际工程中，一般都是将单人步行力按照一定的方式叠加得到多人甚至人群步行力。由于行人间步行不一致，不同人的步行力可能相互抵消，按照荷载等效原则，人数为n的人群荷载可折减为NP个步调一致的行人产生的荷载。2006年10月法国交通部在Matsumoto[3]研究的基础上，提出等效人数Np的计算公式：

式中：n为行人总数量；ξ为振型阻尼。

2.2 人行荷载作用下的结构振动

(1)模态分析

采用MIDAS Gen软件建立有限元分析模型，进行模态分析，结构的前5阶振型模态见图2，其中第1阶、第4阶振型为楼板竖向振动主振型，对应的相对变形最大的节点分别为134号节点、97号节点(图3)，因此对第1阶、第4阶振型振动进行控制。

(2)人行荷载的布置及分析工况

针对结构两个竖向振动主振型，分别考虑最不利单人连续行走荷载和人群荷载两个分析工况。人群均布荷载加载位置为圆环通道区域，单人行走荷载加载位置为各阶振型变形较大位置(图3)，动力加载工况见表1。人群荷载采用等效人数进行计算，此时单人行走时产生的竖向作用力取0.28kN[4]。

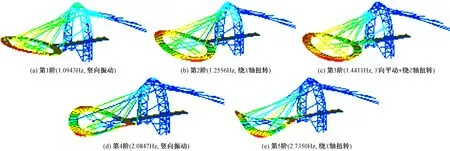
图2 结构前5阶振型

动力加载工况表1

(3)分析结果

根据上述定义的分析工况，应用模拟的荷载曲线，进行人行荷载激励下的动力响应分析，表2给出了各工况作用下结构的加速度峰值。

各工况作用下结构的加速度峰值表2

图3 人行荷载加载区域

工况2，4下结构在人群荷载作用下引起共振，在工况2下结构竖向加速度峰值达1.532m/s2。根据《建筑楼盖结构振动舒适度技术标准》(JGJ/T 441—2019)，参考连廊舒适度限值的规定，不封闭连廊的竖向峰值加速度应小于0.5m/s2，因此结构在人群荷载作用下不满足舒适度要求，需采取附加措施进行振动控制。

3 人行荷载作用下的振动控制

调谐质量阻尼器(Tuned Mass Damper，简称TMD)在控制结构振动方面是一种有效的减振装置，由主结构和附加在结构上的子结构(固体质量和弹簧减振器等)组成。图4是等效的单质点主结构在外部激励P(t)作用下的TMD减振原理示意图，其中m为主结构质量，kd是弹簧减振器的有效刚度，TMD系统的阻尼Cd由黏滞阻尼器提供，其值及TMD系统调频质量md的大小根据计算确定。一般来说，装设一个子结构，只能对以某个频率为主(卓越频率)的外部激励进行有效减振控制。

图4 TMD减振原理示意图

3.1 TMD的布置

采用TMD对工况2、工况4下结构的竖向振动加速度进行控制，根据结构竖向振型模态，将TMD布置在结构对应振型加速度响应最大处(图5)，经试算调整，最终得到TMD布置个数及相关参数见表3[5-6]。

图5 TMD布置图(网格填充区域)

TMD计算参数表3

3.2 减振效果

按表2定义的人群荷载工况进行分析，安装TMD后，各荷载工况下结构的加速度明显减小，且随时间推移结构竖向加速度响应趋于稳定，最终控制在0.5m/s2以下，减振效果良好(表4)。

图6 模拟脉动风速时程曲线

图7 模拟脉动风速时程对应功率谱与Davenport功率谱

图8 模拟脉动风压时程曲线

TMD减振效果表4

4 结构在风荷载时程下的振动特性

工程位于山地地区，地形地貌较复杂，海拔高、大悬挑，结构极易在风场下发生振动。因结构体型复杂，采用时域分析法进行风振分析[7]。利用MIDAS Gen软件，根据数值风洞模拟得到的体型系数及Python编程模拟的风荷载时程，进行风振分析。

4.1 风荷载的时域模拟及其结果

模拟得到的脉动风速时程曲线见图6，此模拟脉动风速时程对应功率谱与Davenport功率谱的比较见图7。由图7可以看出，模拟功率谱和Davenport功率谱的趋势和数值均较接近，模拟效果较好。

模拟得到的脉动风压时程曲线见图8。风速与风压皆根据相同原理生成，但二者之间并无对应关系[9]。

4.2 风荷载方向及体型系数

根据本工程的数值风洞模拟报告，风向角为30°时，挑台所受的竖向风荷载合力最大，为156.6kN，对应的体型系数分布简化见图9。

图9 30°风向角下风荷载体型系数分布简化图

4.3 风振时程分析

保留人行荷载作用下TMD的布置，利用MIDAS Gen软件进行结构风振时程分析，结构的竖向加速度峰值见表5。

需要注意的是，生成的风压时程对应于50年一遇的风压，而根据《高层民用建筑钢结构技术规程》(JGJ 99—2015)[10]3.5.5条规定，在进行风振舒适度验算时，需采用10年一遇的风压。根据两种风压的比例关系，将生成的风压时程转换成可以用于舒适度验算的风压时程，再进行风振时程分析(工程所在地10年一遇的基本风压为0.20kN/m2，50年一遇的基本风压为0.30kN/m2)。

风向角30°时各工况下结构的加速度峰值表5

竖向振动主振型对应相对变形最大的134号节点、97号节点在风荷载作用下的加速度时程曲线如图10所示，加载时间为200s，图中截取典型段，共100s。

由表5及图10可以看出，结构在风荷载作用下的竖向加速度峰值为0.168m/s2，小于规范限值0.5 m/s2，满足舒适度要求，风荷载作用下无需额外附加结构减振措施。

图10 风荷载作用下节点加速度时程曲线

图11 97号节点加速度时程曲线

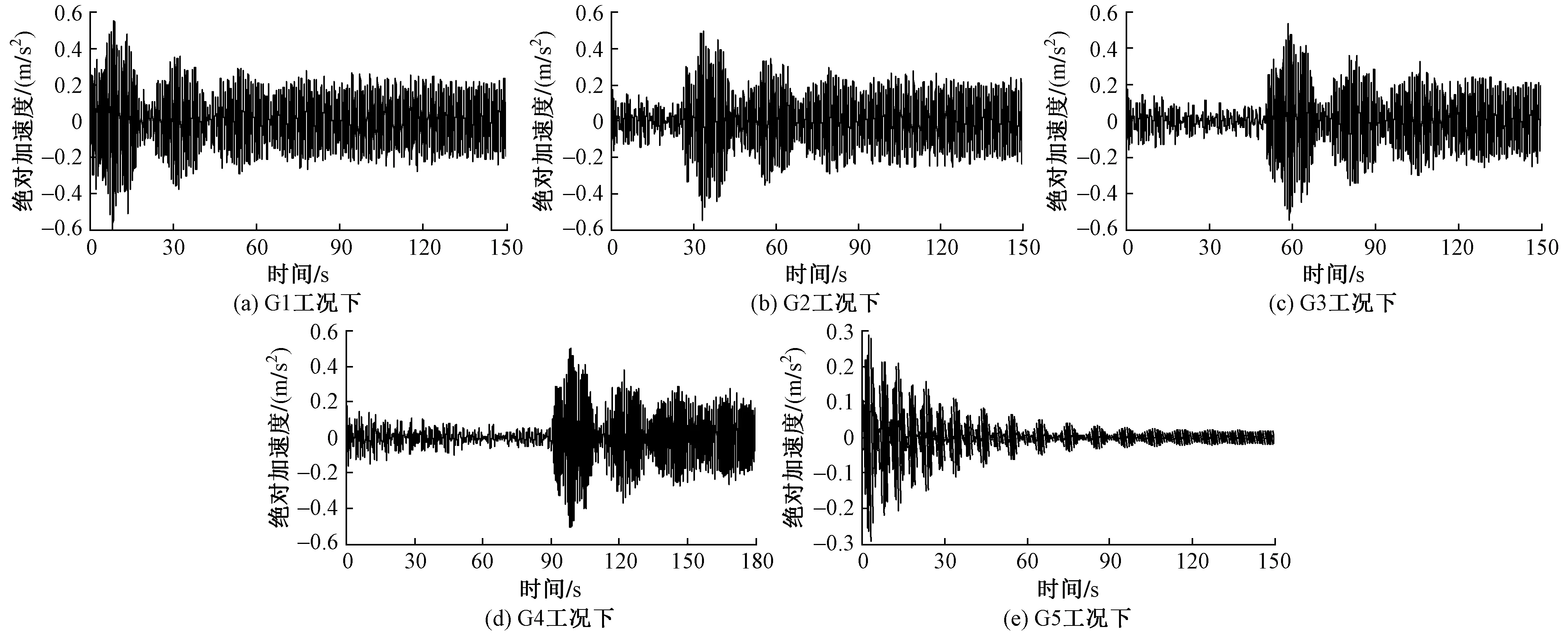
图12 134号节点加速度时程曲线

5 人行荷载及风荷载共同作用下的结构振动

考虑到人行荷载和风荷载在挑台使用阶段可能经常同时存在，因此需要考虑挑台在人行荷载和风荷载共同作用下的舒适度问题，其中减振措施按人行荷载作用下的TMD布置。脉动风压时程与人行荷载共同作用下的结构振动响应依赖于二者激励时程起始时间点的选择。由于脉动风压时程相较于人行荷载具有随机性的特点，因此考虑改变人行荷载的起始时间来分析两者共同作用下的结构振动。

人行荷载工况2的结构响应明显大于工况4，分析时仅考虑工况2。人群荷载及风荷载同时加载的工况，记为G1；人群荷载在第25s开始加载的工况，记为G2；人群荷载在第50s开始加载的工况，记为G3；人群荷载在第90s开始加载的工况，记为G4；仅含人群荷载的工况，为G5；仅含风荷载的工况，为G6(图10)。分析结果见图11、图12及表6。

各工况作用下控制点的加速度峰值/(m/s2) 表6

由图11、图12及表6可知：1)当人群荷载和风荷载共同作用在本结构上后，某个时间点节点加速度峰值会大于0.50m/s2或接近0.50m/s2，但在约10s后结构振动均能逐渐趋于稳定，节点加速度小于0.4m/s2，并最终稳定在0.2m/s2左右，小于规范限值0.5m/s2，可不再另行进行TMD减振设计。2)在本次分析中，人群荷载和风荷载共同作用下(工况G1～G4)楼板峰值加速度均大于人群荷载、风荷载分别作用时相应的峰值加速度之和，表明人群荷载和风荷载存在相互耦合效应，有必要进行两种荷载共同作用下的舒适度分析和振动控制。