高层剪力墙结构最大层间位移角的优化策略

白若冰

(厦门合立道工程设计集团股份有限公司， 厦门 361004)

0 前言

我国现行《高层建筑混凝土结构技术规程》(JGJ 3—2010)[1](简称高规)中，对风荷载或多遇地震标准值作用下，高层建筑楼层的弹性层间位移角作出如下规定：

Δui/hi<[θ]

(1)

式中：Δui为水平荷载作用下第i层的层间位移；hi为层高；[θ]为层间位移角限值。

结构的顶点侧移Δ由各层的层间位移累加而成，而总高度H为各层层高之和。变换后不难发现，高规通过限制层间位移角，一并控制了结构的整体挠曲变形。

(2)

高层建筑的挠曲变形由整体性质所决定，与隐含在体系内的最薄弱部位无关。有外国学者指出：“刚度要求可能比强度要求更为严格的事实，避免了许多结构的设计沦为完全荒谬的工序。因此，如果使得结构的刚度足以满足预期功能，那么它极可能也具备足够的强度”[2]。由于地震作用的不确定性及其作用效应难以估量，比起大量预测构件强度以期找出体系内最薄弱环节的设计方法，预测整体刚度的设计方法较易于实现并且更为可靠。层间位移角作为衡量结构刚度与变形能力的首要指标，在控制整体刚度上起着不可替代的重要作用。

刚度的大小亦时刻关系着结构整体经济指标。焦柯等[3]通过调整某百米高层剪力墙住宅的结构布置，对比分析了小震作用下，满足不同层间位移角限值(1/1 000，1/1 300和1/1 600)时结构方案的材料用量(包括混凝土与钢筋)，得出当指标趋于高规限值(1/1 000)时材料总造价最为经济的结论。

国内部分学者认为，我国规范对层间位移角限值的取值过于严格[4]，加之部分工程师的控制力不足，建筑物刚度过大的情况难以避免，不光影响项目经济性，还造成地震反应激增，反倒不利于抗震。

笔者认为，在现有规范体系下将高层剪力墙结构的最大层间位移角指标贴近于高规限值是有实际意义的：一方面，避免建筑的刚度富余过多，力求抗震安全；另一方面，合理控制项目造价，尽可能实现结构在必须承受的载荷与经济成本间的最优化。

基于上述思考，本文将重点研究高层剪力墙结构最大层间位移角的优化策略，并结合算例进行验证，以供结构同仁参考使用。

1 最大层间位移角的优化思路

如图1所示，楼板刚性情况下，高层剪力墙结构的层间位移角θi由层间平动位移角θia和扭转位移角θir叠加而成，即：

θi=θia+θir=(Δuia+Δuir)/hi

(3)

图1 层间位移角的构成

(4)

2 顶点平动侧移的敏感性曲线

2018年，本文的前期研究[5]证明了高层建筑最大层间平动位移角与顶点平动侧移的强相关性。这使得笔者将注意力集中到后者身上，转而建立起研究结构布置方案与顶点平动侧移关联的分析框架。

如果采用平面布墙率指标n来大致评估百米以内高层剪力墙结构的横墙和翼墙(满足有效翼缘宽度要求的纵墙)总截面面积占楼层面积的比例关系，可以发现其比值并不大，通常在4.5%～7.5%之间。因此，笔者利用图2所示的薄壁箱形截面来模拟结构平面布置方案。

图2 薄壁箱形截面

对于任一给定的高层建筑(楼层平面长度b、宽度h与高宽比H/h均为定值)，当仅考虑单向水平荷载作用(图2中的Y向)时，横墙提供的侧移刚度仅由腹板厚度尺寸系数α决定；而翼墙的刚度贡献只与翼缘厚度尺寸系数β有关，且两者互不干扰。理论上讲，任一结构布置方案均存在与之唯一对应的尺寸系数α，β，干预两者的数值相当于调整了平面的横、翼墙布置。

结合水平倒三角形荷载q下的竖向悬臂梁简图，就能从宏观上建立起弹性状态下规则对称的高层剪力墙结构，其结构布置方案与顶点平动侧移Δa的数学联系，理论公式如下：

(5)

式中：EJd为实际侧移刚度，EJd=EIb/(1+3.64γ2)；EIb为弯曲刚度，EIb=[1-(1-2α)(1-2β)3]Ebh3/12；E为材料弹性模量；尺寸系数α=bw/b和β=bf/h；bw，bf为薄壁箱形截面的腹板、翼缘厚度；而剪切变形影响系数γ2可由下式求得：

(6)

各高宽比下的结构调整方案 表1

地震作用下，敏感性指标不受水平地震影响系数最大值αmax和场地特征周期Tg取值的影响，但结构刚度调整引起地震荷载变化的影响不可忽略。笔者在前期研究中推导了高层剪力墙住宅的地震荷载qE计算公式：

(7)

以及顶点平动侧移公式：

(8)

式中：剪力墙总面积A=2bh(α+β-2αβ)，其值从宏观上表征了结构自重G。利用上述公式，图3(b)给出了地震作用下的顶点平动侧移敏感性指标曲线。

图3 顶点平动侧移的敏感性曲线

必须指明的是，该曲线建立在结构自重随刚度优化而减小(两者的相对关系将在第3章中讨论)的假定之上，并不适用于某些特殊调整手段(例如对剪压比超限的连梁进行点铰处理)。在此期间，结构上部自重并无变化，而整体刚度有所削弱。针对这种情况，笔者补充了自重未随刚度变化(即A为定值)时的算例，并于图3(c)中绘制出相应曲线。

3 最大层间平动位移角的优化策略

当结构的最大层间位移角存在富余时，为使指标贴近高规限值，需减少水平抗侧力构件的材料用量以增大其平动位移。合乎效率与经济性的策略是，减少材料用量的同时，控制位移角指标的降幅不多。换言之，应优先采用两种调整方向中顶点平动侧移增量较小的方案。

众所皆知，高宽比从宏观上决定了结构在水平荷载下的侧移变形。结构矮墩时高宽比小，受力时难以整体弯曲，故呈现为弯剪型；结构细长时高宽比大，侧向力下更易于挠曲，因而呈现为弯曲型。

图3的数据同时表明，高宽比也是指引结构优化调整方向的决定性指标。工程实践中，建筑平面的复杂性常常使得高宽比难以简单求出，而侧移变形的直观性令其替代高宽比，成为良好的观察指标。

图3亦指出最大层间平动位移角的优化思路：首先，确定各向的侧移变形形态。以某项目为例(图4)，X向变形曲线存在反弯点，可确认为弯剪型；而Y向曲线未见有反弯点，故确定为弯曲型；其次，采用针对性的调整方案。弯剪型变形时，应执行优化翼墙的调整方案；而弯曲型变形时，优化横墙的调整方案则是最佳选择。

图4 某剪力墙结构的双向侧移变形曲线

值得讨论的是，图3(b)中部分调整方案的顶点平动侧移并未随刚度削弱而增大，暗示可能存在更为高效的优化调整手段。究其原因，如式(9)所示，地震作用下顶点平动侧移敏感性指标的变化趋势受制于两个关键变量的相对关系：结构的自重优化率GΔ=(A*-A)/A和刚度优化率KΔ=(EJd*-EJd)/EJd，其中A*，EJd*分别为优化后的剪力墙总面积、实际侧移刚度。

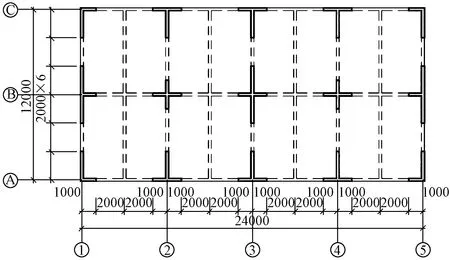
(9)

结合图3(b)中，地震作用下顶点平动侧移敏感性指标曲线的算例成果(表2)，可以发现敏感性指标异常是由地震反应力较实际侧移刚度下降更快而引发，根本原因是结构自重的降幅高于刚度降幅(即GΔ

其次，利用水平抗侧力墙体在刚度上的“马太效应”(强者恒强，弱者愈弱)现象，削减对整体结构刚度贡献弱的低效墙体。前期研究[5]表明，相较其他横墙，占据建筑最大面宽的组合横墙，在同等墙体材料用量下对于结构整体刚度的贡献是最大的；且增设等量墙材时刚度的增幅亦最高，是增强上部刚度的首选载体。这种强者使之愈强的结构调整策略，是“马太效应”理念运用于工程实践的典型案例之一。逆向思考之，刚度优化时识别并削减对整体自重拖累大于刚度贡献(保证GΔ

最后，执行基于侧移变形形态的最大层间平动位移角优化思路(简称为优化思路)。前述两个步骤实施后，最大层间平动位移角应有所减小，为进一步优化水平抗侧力构件提供了空间。若能预知位移角指标与调整方向的敏感性关联，从中选择指标增幅最小的调整方案，便能高效地实现优化目标，而优化思路则为此提供了决策依据。

λ=1.5%时顶点平动侧移敏感性指标值及其构成 表2

4 算例

图5所示的简化算例，可直观校验上述策略的有效性。某高层建筑，标准层层高3.0m，建筑总高度99m；抗震设防烈度为7度，设计基本地震加速度值为0.15g，设计地震分组为第三组，建筑场地类别为Ⅱ类，特征周期为0.45s，剪力墙抗震等级为二级；50年一遇基本风压为0.50kN/m2，地面粗糙度为B类。

各层剪力墙厚度为200mm；Y向连梁宽度同墙厚，高度均为700mm；X向框架梁尺寸为200mm×600mm；次梁截面统一为200mm×550mm，楼板厚度均为130mm。平面内竖向构件布置均匀、对称，结构刚度中心与质量中心完全重合，层间位移角与顶点侧移均为完全平动下的结果，亦代表着层间平动位移角与顶点平动侧移。

图5 原方案结构平面图

原方案Y向的控制工况为地震工况，对应的最大层间位移角为1/1 014(表3)，已接近高规限值(1/1 000)，结构方案看似经济合理。但不难发现，上部自重仍有所富余(板厚过厚)且平面中存在低效墙肢，说明结构存在优化空间。依据优化策略建议，实施了如下工作：

步骤一：减薄板厚至120mm，在实际侧移刚度未受较大影响的情况下将最大层间位移角降低至1/1 025。

步骤二：去除平面内的低效墙体(图5中阴影部分墙肢)，以控制地震反应力降幅高于上部刚度的降幅，进一步将最大层间位移角减小至1/1 036。

结合表4可以看到，上述调整过程中结构自重降幅远高于刚度降幅，从而高效约束了地震作用下的最大层间位移角，实现了预期优化目标。

步骤三a：观察图6可知，Y向的侧移变形为弯曲型，故选择②轴、④轴的横墙进行微调，如图7(a)所示；步骤三b：以消减同轴上的等长翼墙作为对比方案，如图7(b)所示，两者的计算结果汇总于表3和表4中。

图6 地震作用下结构的双向侧移变形曲线

图7 结构Y向调整方案

步骤四：延续上述思路，进一步消减②轴、④轴的横墙，如图7(c)中所示。与步骤三b中的调整翼墙方案相比，在层间位移角相对较小的情况下，墙肢消减长度增加一倍，实现了优化材料用量的目的。

在此期间，观察Y向风荷载作用下结构最大层间位移角与顶点侧移的变化规律(表3)，可知两者仅受上部刚度变化的影响，而自重变化的影响可忽略不计。指标变化趋势亦证明，上述优化思路对于

Y向最大层间位移角和顶点侧移计算结果 表3

Y向各优化步骤下的计算结果对比 表4

风荷载是同样有效的。

演算至此，结构方案的中间成果如图8所示。结合表5可知，Y向最大层间位移角虽已贴近高规限值，但X向指标仍有所富余，可适度进行优化。

步骤五a：观察到图6中X向的侧移变形为弯剪型，故选择轴交①轴、⑤轴处的翼墙(同为Y向抗侧力体系的横墙)略作调整，如图9(a)所示；步骤五b：在相同位置的横墙(亦是Y向的翼墙)上消减等量墙体以作对比，如图9(b)所示。两者的计算成果均见表5。

图8 中间方案结构平面图

图9 结构X向调整方案

双向最大层间位移角和顶点侧移计算结果 表5

比较数据后可知，当结构高宽比不大时，严格执行优化思路所建议的调整方案，同样可使最大层间位移角的削弱幅度降至最低。

综上所述，简化案例的结果与理论研究完全相符，本文提出的最大层间平动位移角优化策略在工程实践中是可靠且高效的。值得一提的是，表3和表5中各方案的顶点侧移与最大层间位移角均呈现出强相关性，可见前者的变化趋势决定了后者的指标走向。

各优化步骤下的材料用量对比 表6

由表6可知，优化过程中结构的混凝土用量减少较快，而钢筋用量则缓步上升。可见，随着最大层间位移角趋近于高规限值，剪力墙用钢量逐渐降低，而梁用钢量则逐渐增加。不过，得益于混凝土用量的大幅优化，整体结构的材料总造价逐步下降，达到了高效节省结构材料的目的。

5 结论

(1)考虑到层间平动位移在层间位移中占据主导地位，最大层间位移角的优化研究，必然起步于最大层间平动位移角的优化研究之上。

(2)地震作用下，结构优化的目标在于控制上部自重降幅快于刚度降幅。削减非水平抗侧力构件重量或去除低效墙体均是有效手段。

(3)风荷载或地震作用下，基于侧移变形形态的最大层间平动位移角优化思路为高效地实现优化目标提供了决策依据。