初始角度对平板自由下落运动的影响

梁 彬, 张石玉, 付增良

(中国航天空气动力技术研究院, 北京 100074)

引 言

气动力和运动耦合作用、 以及非定常流动现象的存在, 使得平板的自由下落成为一个经典的流体力学-动力学耦合问题, 一直以来都有相关的研究. 由于下落过程中常常出现运动的不确定性, 该问题也是一个典型的非线性问题. Maxwell[1]最早定性解释和描述了纸片的自由翻滚下落运动. Anderson等[2]和Pesavento等[3]结合实验和计算方法, 针对二维平板的下落问题建立力学模型, 解释了其中的非定常气动力机制, 并分析了实验和计算结果之间存在差别的原因. Belmonte等[4]、 Assemat 等[5]都详细研究了二维平板自由下落中不同的非定常运动轨迹, 并研究了影响运动轨迹的参数. Wan等[6], Tian等[7-8]、 Kubota等[9]详细研究了平板自由下落中的流动涡结构和发展过程. Belmonte等[4]、 周琪[10]、 蔡琛芳等[11]还获取了二维平板不同下落运动之间, 如翻滚和摆动两种规律性运动间的转变临界参数. 蔡琛芳等[11]研究了不同质心位置对平板下落运动轨迹的影响. 同时, 平板的自由下落问题也是植物种子散播[12-14]、 纸片、 叶片飘落、 气泡上升[15]、 昆虫飞行[16]、 仿生扑翼飞行器[17-18]等自然现象和工程应用的简化物理模型以及基本原理体现, 具有一定的研究价值.

无论采用实验还是数值计算模拟方法, 上述以往的研究都集中在下落过程的周期性振荡, 对下落过程中出现的非线性现象研究很少, 一般采用同一初始状态、 或是简单对比几个初始状态的影响后选取一个开展研究. 而平板下落作为一个非线性系统, 初始状态的改变是否会影响下落过程的发展路径以及最终的现象还不清楚. 本文在上述研究的基础上, 以二维平板自由下落问题为对象, 采用基于动网格技术的数值模拟方法, 深入研究了初始角度对下落运动的影响. 希望通过研究发现非线性运动何时出现、 非线性运动如何演化、 以及周期性运动会在何时出现.

1 方法

1.1 坐标系和参数

本文定义了固连于地球的惯性坐标系(x,y)描述平板的运动和姿态. 如图1所示, 坐标原点位于初始状态时平板质心,x为水平方向, 指向右侧;y为垂直方向, 指向下方. 定义u,v分别为平板运动速度在x,y轴上的两个分量;ω为平板转动角速度, 逆时针为正;θ为平板转动角度, 即平板与水平面的夹角, 逆时针为正. 定义Fx,Fy分别为x,y轴上的气动力分量;M为气动力矩, 逆时针为正;m为平板质量;I为平板转动惯量;g为重力加速度； 平板宽度为L, 厚度为h.

图1 坐标系和状态变量示意图Fig. 1 Definition of the state variables and sketch of the reference frame

1.2 运动方程和流体力学方程

根据前文惯性坐标系和动力学参数定义, 二维平板在惯性坐标系下的运动方程可描述如下

(1)

求解运动方程(1)还须已知其中的气动力和气动力矩部分, 气动力和气动力矩是由流体力学方程所控制的, 如下

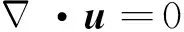
(2)

(3)

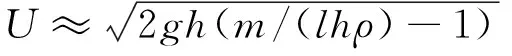
(4)

(5)

1.3 模拟方法和计算网格

本文采用的刚性动网格、 流体力学方程的数值求解方法、 流体力学方程和运动学方程耦合求解方法与文献[11]相同, 不再赘述. 计算模拟方法在文献[11]中通过与实验结果Andersen[2]的对比, 得到了较好的验证. 采用的平板模型与文献[2]和[11]一致, 即宽厚比为14的二维平板, 平板边角处进行了倒角处理, 便于网格生成. 平板外形和计算网格如图2所示.

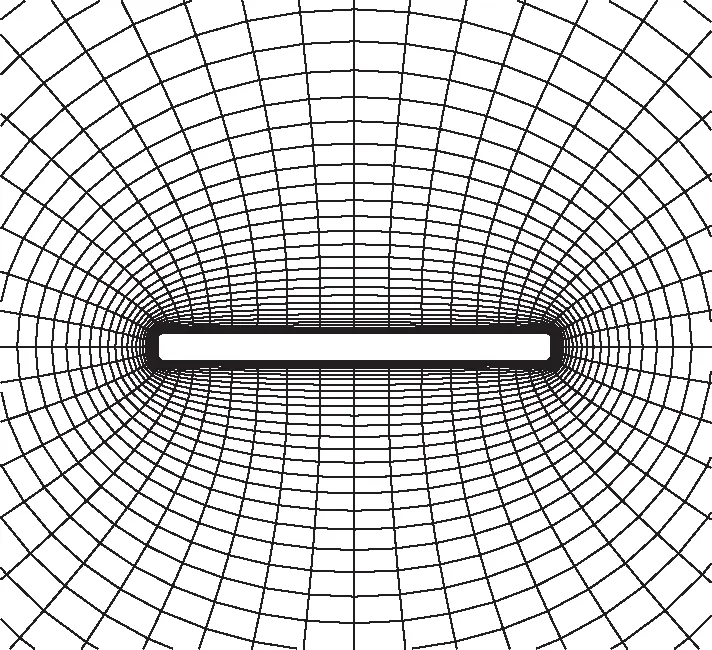
图2 平板外形和计算网格Fig. 2 Plate shape and computational grids

1.4 分析方法

之前的研究结果表明[11], 平板的自由下落过程在气动力和惯性力的共同作用下可呈现周期性的翻滚或摆动, 为非保守自洽非线性系统. 针对其运动特点, 本文采用相平面法和频谱分析方法分析和描述了平板的自由下落运动.

为了准确描述平板下落过程中不同下落状态的频域特征, 本文还采用了频谱分析方法分析平板角度的周期性变化, 有关频谱分析和Fourier变换原理见文献[20].

2 初始角度对摆动运动的影响

基于之前的研究基础[11], 当平板转动惯量较小(I+<0.95)时, 下落时呈规律摆动, 摆动周期随转动惯量增加而增大. 为了研究初始角度对摆动运动的影响, 选择了无量纲转动惯量I+<0.95时几种摆动运动进行模拟, 其他参数分别为: 宽厚比L/h=14, 无量纲质量m+=0.385 7,Re=2 094.

2.1 典型算例结果和讨论

图3显示了I+=0.03时, 平板以不同初始角度释放后自由下落的θ-ω+相轨迹和无量纲速度u+-v+曲线, 图4以其中的初始角度20°, 60°和80°为例直观显示了平板自由下落轨迹, 图5以过渡状态较长的初始角度20°和80°为例给出了平板下落过程中角位移振荡过程的频谱分析结果. 可以看到, 在自由下落的初期, 不同初始角度下平板呈现不同的运动状态和轨迹(见图3中虚线部分, 图4), 这一段状态可称为过渡下落状态. 经过过渡下落状态的运动过渡之后, 平板后期最终呈现规律的周期性摆动运动(见图3中实线部分, 图4), 且各个初始角度下最终的周期性摆动运动状态和轨迹是一致的: 在u+-v+曲线上体现为重合的“∞”形轨迹, 在θ-ω+相轨迹上形成重合的稳定极限环(见图3中实线部分), 在频谱分析结果中最终的周期性运动角位移振荡主频均为2.123 Hz(见图5). 此时平板的运动是周期性的, 这一段状态可称为周期性下落状态. 因此, 平板的初始角度并不会改变平板最终的周期性摆动下落运动状态.

在初期过渡下落状态中, 虽然平板的状态与最终的周期性规律摆动运动并不相同, 但是是相似的, 仍然是一种摆动运动. 从图3中虚线部分可以看到, 初期平板仍然按照“∞”形轨迹运动, 只是“∞”形轨迹并不对称. 这一现象在平板下落轨迹图中(见图4)也得到直观体现. 其中, 一些初始角度下过渡状态较长, 如20°时, 平板在过渡下落状态进行了多次非规律性摆动(见图3, 图4), 摆动幅度较小而主频高于周期性状态(2.831 Hz, 见图5); 一些初始角度下过渡状态很短, 如60°时, 在下落轨迹图中几乎看不到过渡状态和周期性摆动状态的区别(见图4), 只能在u+-v+曲线上看出下落初期“∞”形轨迹的不对称(见图3); 一些初始角度下过渡状态较长, 但摆动次数较少, 如80°时, 平板经历了1次较长的摆动后进入周期性下落状态(见图4), 过渡期摆动幅度较大而主频低于周期性状态(1.415 Hz, 见图5).

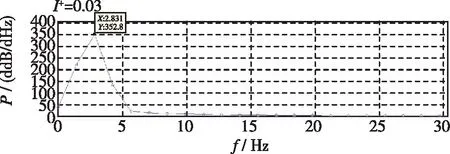
(a) Transitional falling stage at θ0=20°

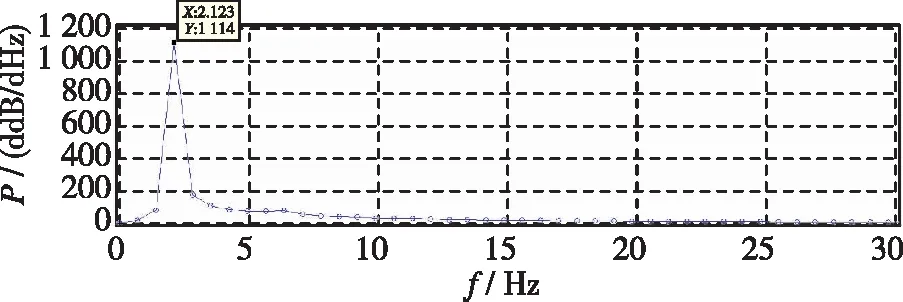
(b) Periodic fluttering falling stage at θ0=20°

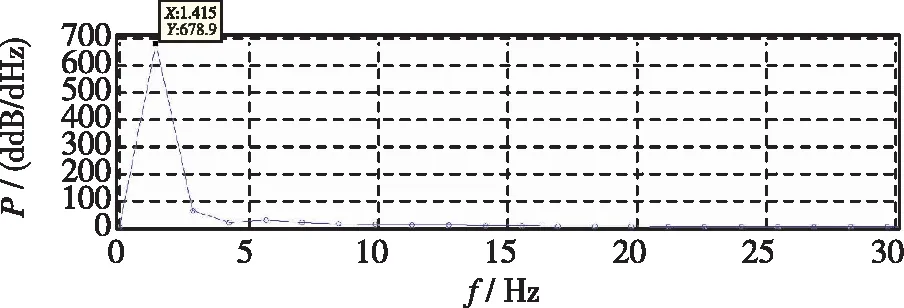
(c) Transitional falling stage at θ0=80°

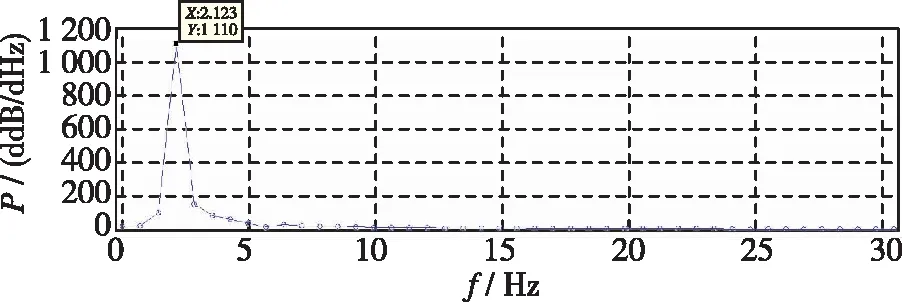
(d) Periodic fluttering falling stage at θ0=80°图5 频谱分析结果(I+=0.03)Fig. 5 Result of spectrum analysis (I+=0.03)

初始角度为负值时, 平板初始姿态其实与初始角度为正值时一致, 只是对称翻转的关系. 自由下落过程中的过渡状态和周期性状态也呈翻转、 相位相反的关系. 图3中同时给出了初始角度为-40°和-60°(即140°和120°)时的结果, 可以看到其曲线分别与初始角度为40°和60°时为左右对称翻转关系. 初始角度为负值(或超过90°)时不再重复研究.

图6以初始角度20°为例显示了平板自由下落时的状态变量随时间变化曲线,t+<8时为过渡下落状态,t+>8为周期摆动下落状态.下落开始初期(t+=0～1), 平板在重力作用下向下运动, 运动使得指向左上的气动力和顺时针方向气动力矩作用于平板, 气动力和重力共同作用下导致平板进一步向左下运动并顺时针转动. 当平板角度转为负值后(t+=1～3), 气动力和力矩大小方向也发生了变化, 气动力水平分量指向右侧, 气动力矩变为逆时针方向, 导致平板向左的水平速度减小并逐渐变为向右、 顺时针转动速度减小并逐渐变为逆时针. 由于转动角度为角速度的积分项, 惯性作用下气动力矩的变化反映至转动角度具有一定的滞后. 后续重复了上述变化过程, 直至过渡下落状态过程(t+=0～8)后进入周期性摆动下落(t+>8).可见, 过渡下落状态与周期性下落状态的机理是相似的: 由于平板转动惯量相对较小, 平板的转动角度能够较快地响应气动力矩变化, 形成不断往复的周期性或非周期性摆动运动, 对应其周期性摆动运动和过渡下落状态. 因此, 也解释了模拟结果: 影响平板下落最终运动状态的是转动惯量等关键性参数, 与初始角度无关.

图6 无量纲速度和气动力变化曲线(I+=0.03,θ0=20°)Fig. 6 Dimensionless velocities and aerodynamic force components (I+=0.03,θ0=20°)

图7给出了平板初始为水平或垂直放置时(即初始角度为0°或90°)的结果. 可以看到, 平板初始水平或垂直放置时, 经过一段定常的运动后才进入过渡下落状态, 然后经过较长的过程后才最终进入周期性摆动运动. 周期性摆动运动状态和轨迹与其余初始角度是一致的: 在u+-v+曲线上为形状相同的“∞”形轨迹, 相轨迹也为形状相同的极限环. 原因在于平板下落初期流场对称, 平板未受到气动力矩的作用使其转动. 经过一段时间的误差和干扰积累后, 平板受微小气动力矩作用产生转动, 随后姿态改变导致气动力变化并逐渐进入过渡下落状态, 最终演化为周期性摆动下落. 因此, 平板初始姿态左右对称时也不会影响最终形成周期性摆动下落运动状态.

(a) θ versus ω+

(b) u+ versus v+图7 θ-ω+相轨迹和u+-v+曲线(I+=0.03, θ0=0°, θ0=90°)Fig. 7 θ versus ω+ and u+ versus v+(I+=0.03, θ0=0°, θ0=90°)

2.2 其他摆动运动结果

平板初始角度对摆动运动的影响的其他算例结果如图8～11所示, 分别显示了其他参数不变、 无量纲转动惯量较小(I+=0.01)和较大(I+=0.5)时的θ-ω+相轨迹、 无量纲速度u+-v+曲线和自由下落轨迹.

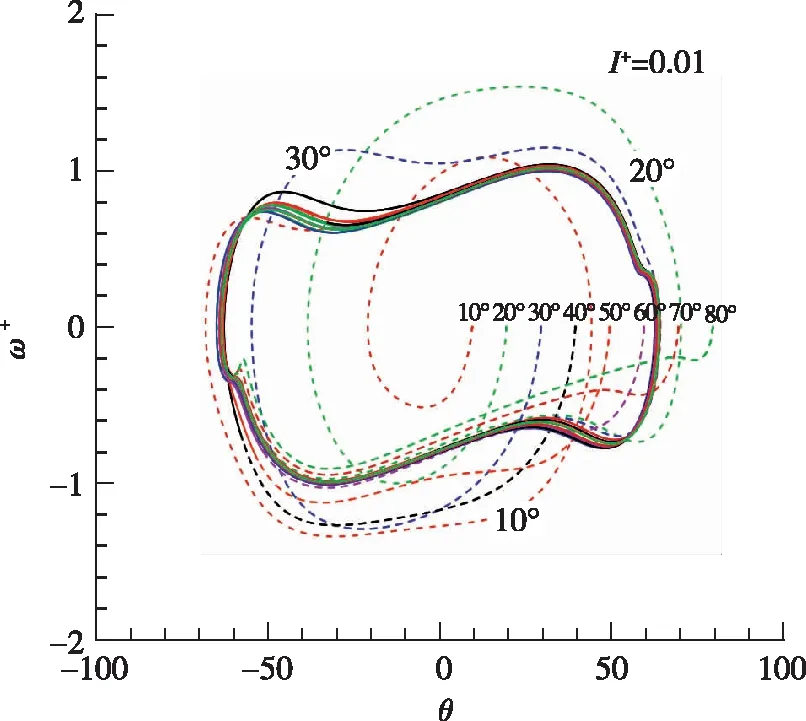
(a) θ versus ω+

(b) u+ versus v+

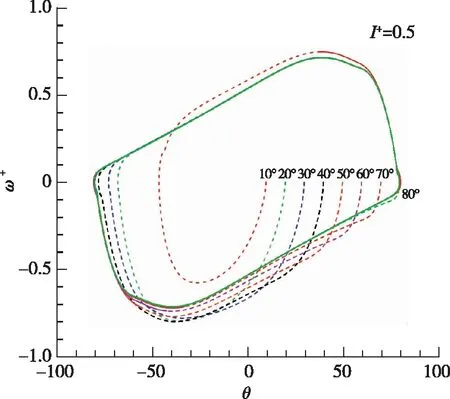
(a) θ versus ω+

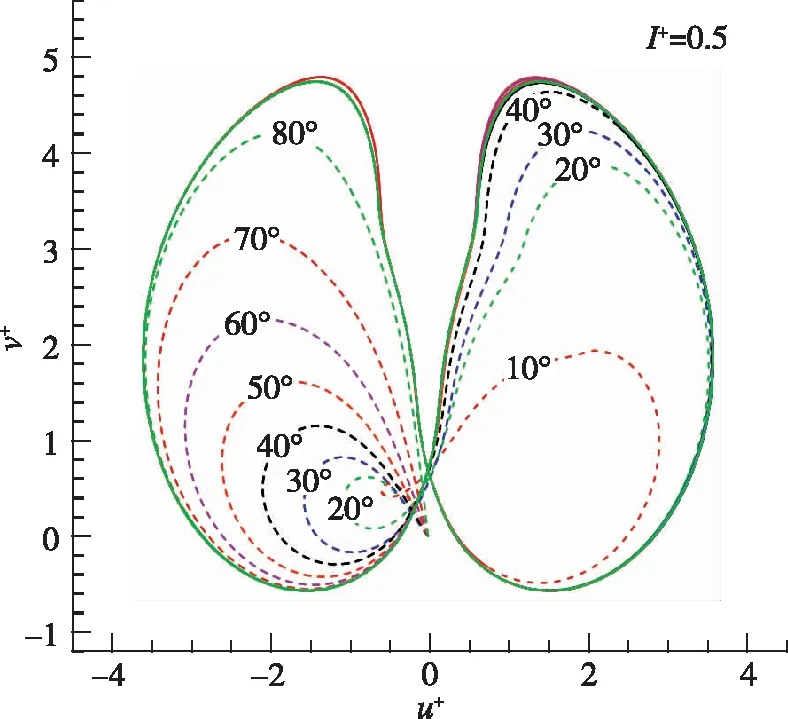
(b) u+ versus v+

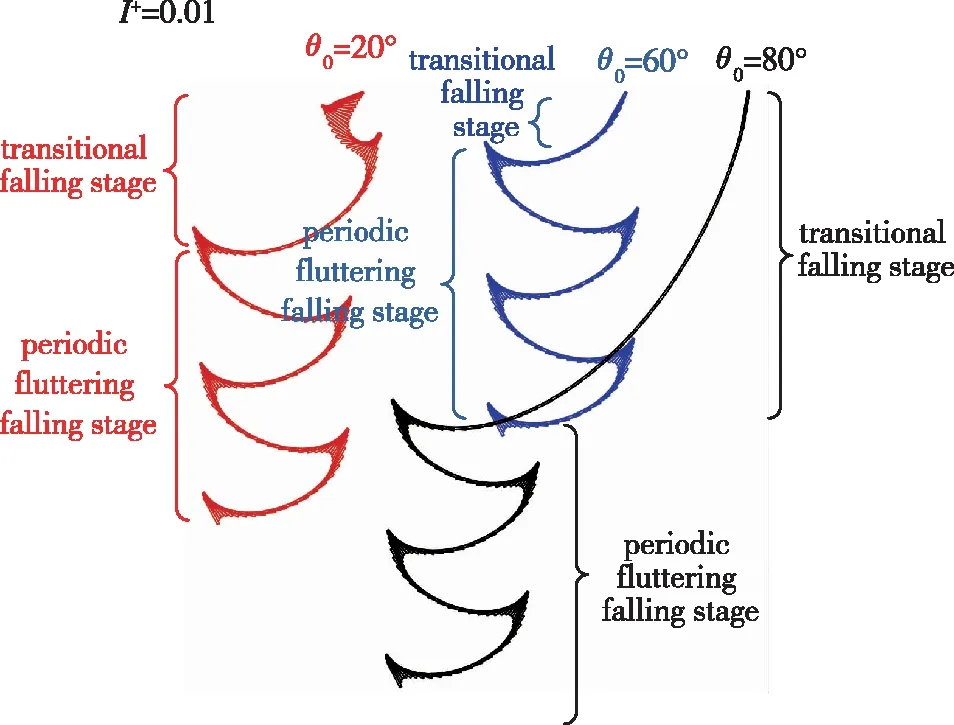
图10 平板自由下落运动轨迹(I+=0.01)Fig. 10 Trajectories of freely falling plates (I+=0.01)

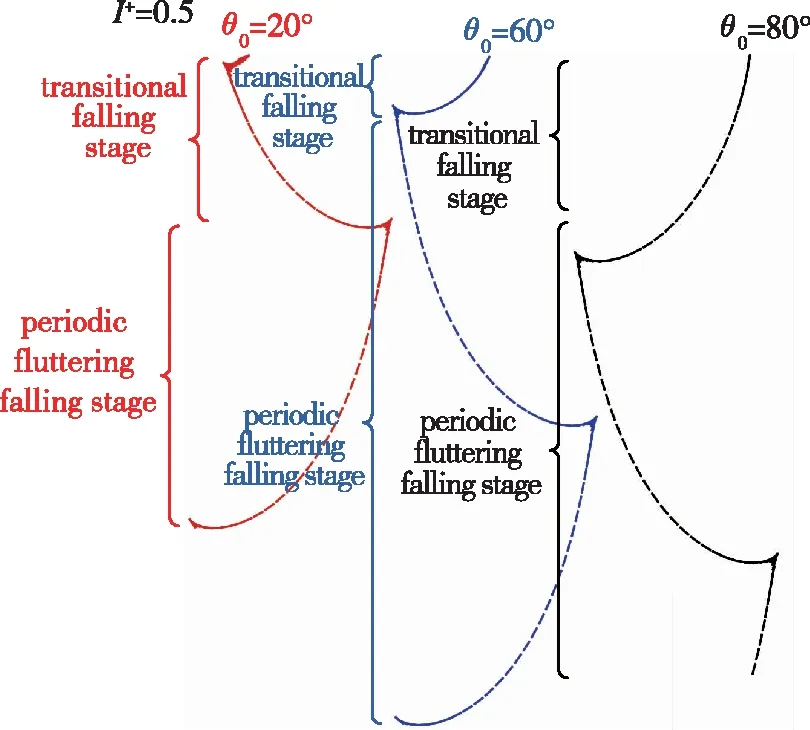
图11 平板自由下落运动轨迹(I+=0.5)Fig. 11 Trajectories of freely falling plates (I+=0.5)

由图8～11的结果可以看到, 与前文典型算例相似: 在自由下落初期的过渡下落状态, 不同初始角度下平板呈现不同的运动状态和轨迹, 但该运动和轨迹与周期性的摆动运动是相似的, 是一种不规律的摆动运动. 平板后期最终呈现规律的周期性摆动运动状态, 且各个初始角度下最终的周期性摆动运动状态和轨迹是一致的. 其中的物理机制也是类似的, 不再赘述.

3 初始角度对翻滚运动的影响

平板转动惯量较大(I+>0.95)时, 平板下落最终呈规律翻滚. 为研究初始角度对翻滚运动的影响, 选择了无量纲转动惯量I+=1.0和I+=5.0进行模拟.图12给出了I+=1.0时不同初始角度释放后的结果, 图13直观显示了典型算例的平板运动轨迹.

(a) θ versus ω+

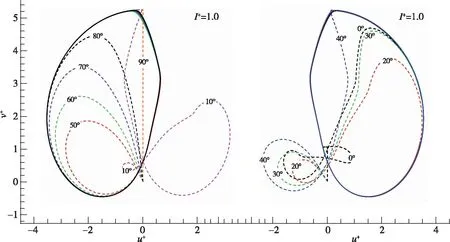
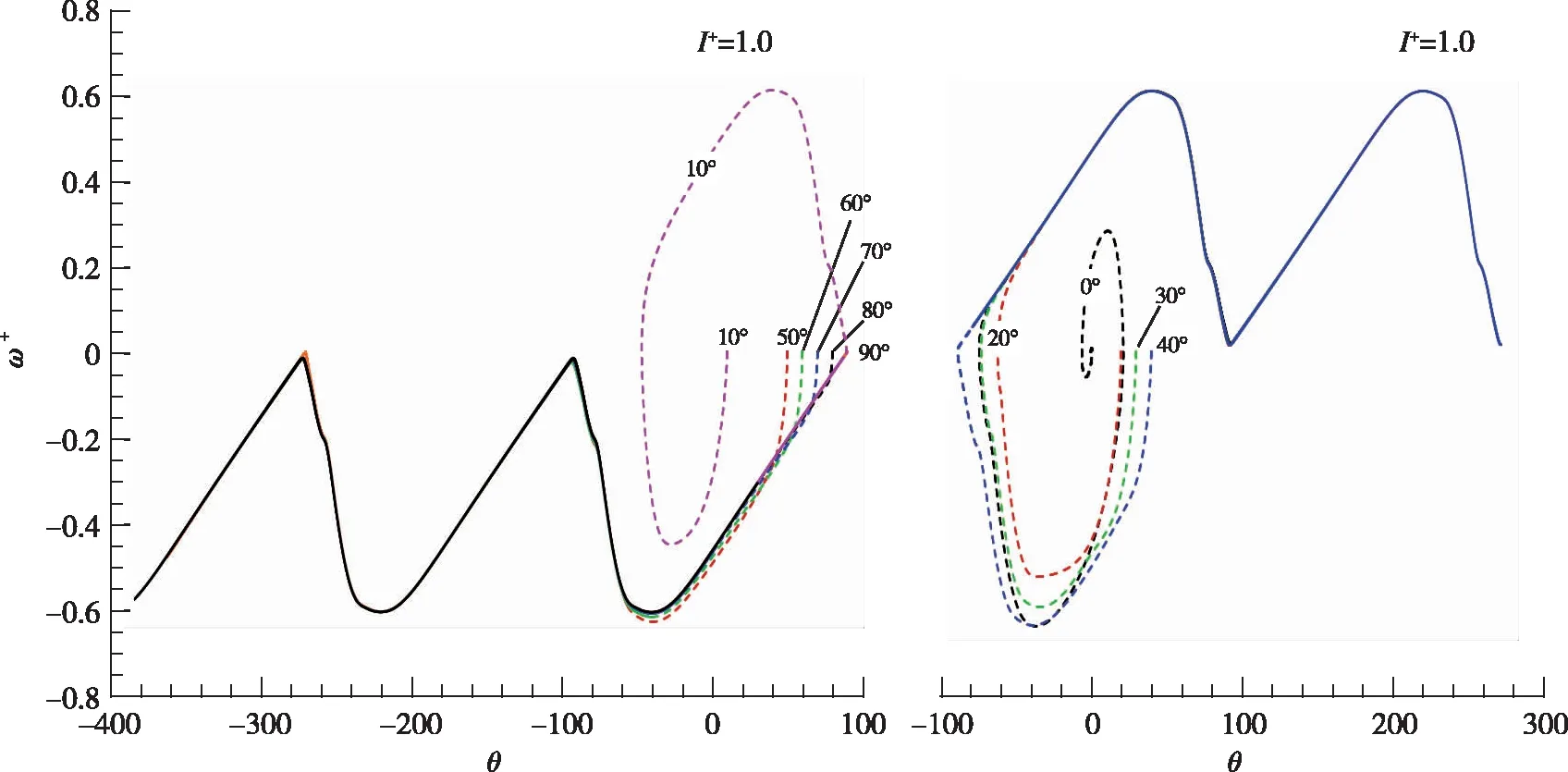
(b) u+ versus v+图12 θ-ω+相轨迹和u+-v+曲线(I+=1.0)Fig. 12 θ versus ω+ and u+ versus v+(I+=1.0)

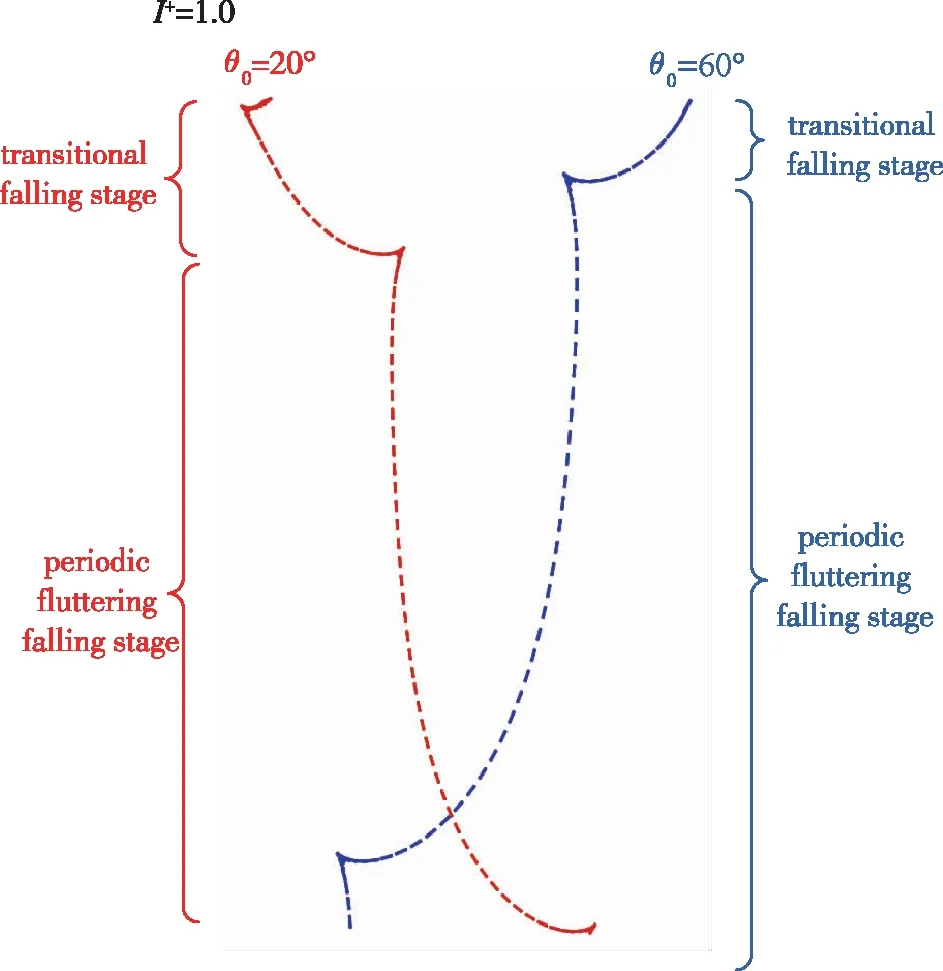
图13 平板自由下落运动轨迹(I+=1.0)Fig. 13 Trajectories of freely falling plates (I+=1.0)

由图12和13的结果可以看到, 与摆动运动的情况类似, 平板的初始角度并不会改变平板后期最终的周期性翻滚下落运动状态. 初期的过渡下落状态中, 不同初始角度下平板呈现不同的运动状态和轨迹(见图12中虚线部分, 图13), 但最终呈现规律的周期性翻滚运动状态, 且各初始角度下最终的周期性翻滚运动状态和轨迹一致:θ-ω+相平面上体现为重合的稳定轨迹;u+-v+曲线上体现为重合的“o”形轨迹.

与摆动运动不同之处在于, 翻滚运动的过渡下落可分为小幅翻滚和非规律性摆动两种状态. 如初始角度≥50°时, 过渡下落状态平板u+-v+曲线是比周期性翻滚运动稍小的“o”形轨迹, 相轨迹上也不存在ω+>0的点, 说明平板一直朝一个方向翻滚、 是一个小幅的翻滚运动, 在平板下落轨迹图中(见图13)也得到直观体现. 初始角度≤40°时, 过渡下落状态是一种非规律性的摆动运动, 在u+-v+曲线上显示为不对称的“∞”形轨迹, 相轨迹呈现非闭轨摆动运动特征. 正是由于过渡下落阶段这种非规律性摆动运动的存在, 使得平板最终周期性翻滚运动的翻滚方向存在差别, 如初始角度约50°～80°间最终周期性翻滚方向与过渡状态小幅翻滚方向相同(顺时针),u+-v+曲线上为左侧“o”形轨迹,θ-ω+相轨迹位于下方; 初始角度10°时经过过渡状态3次摆动运动, 最终周期性翻滚方向为顺时针,u+-v+曲线上为左侧“o”形轨迹, 相轨迹位于下方; 初始角度为0°, 20°, 30°, 40°时经过过渡状态2次或多次摆动运动, 最终周期性翻滚方向为逆时针,u+-v+曲线上为右侧“o”形轨迹, 相轨迹位于上方. 虽然翻滚方向相反, 但平板运动形式和状态无本质变化, 仅为左右对称关系.

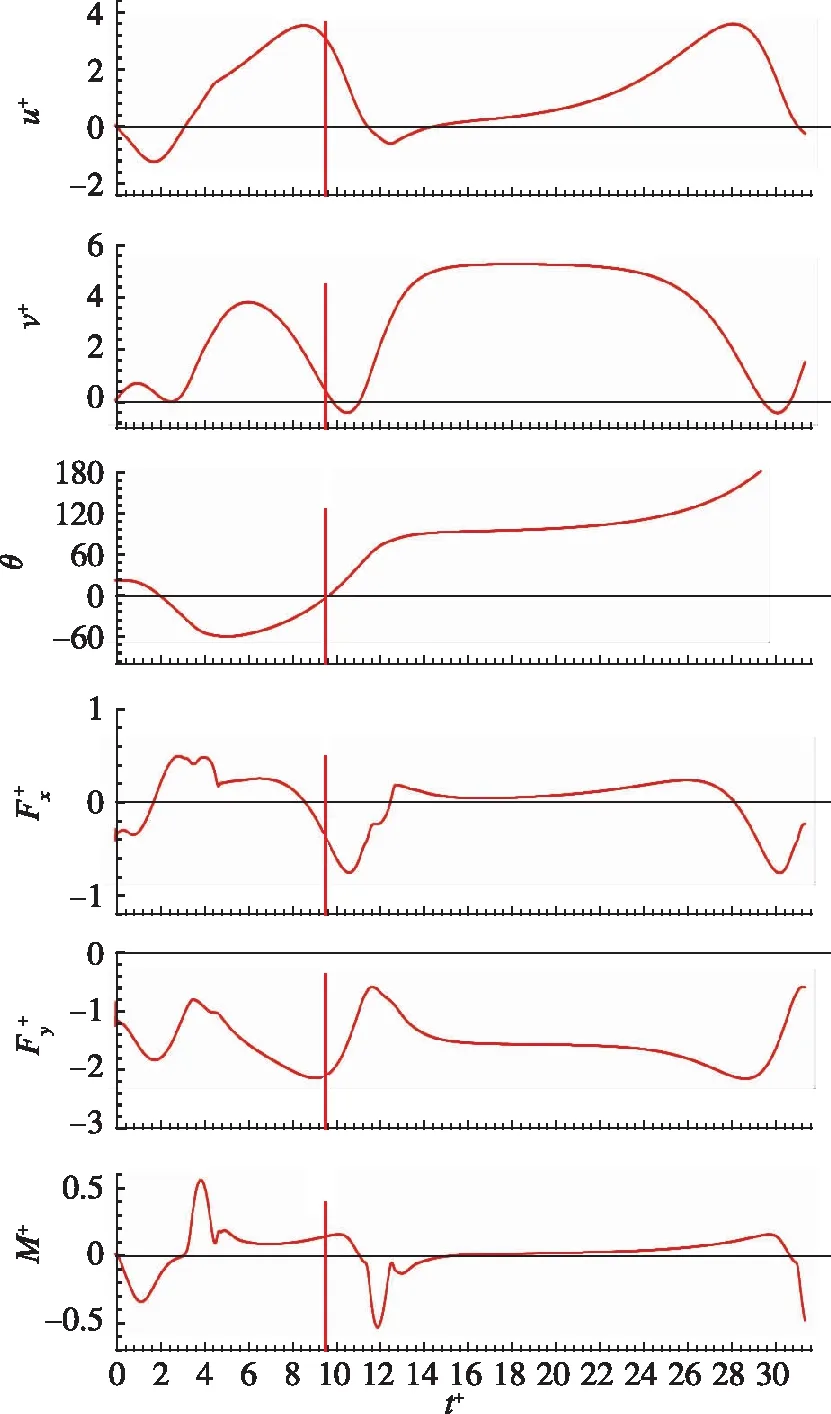
图14 无量纲速度和气动力变化曲线(I+=1.0,θ0=20°)Fig. 14 Dimensionless velocities and aerodynamic force components (I+=1.0,θ0=20°)

图14给出了初始角度为20°时平板自由下落状态变量随时间变化曲线, 分割线左侧为过渡下落状态, 分割线右侧为周期翻滚下落状态. 图14中可以看到, 自由下落初期过渡运动状态中平板的受力和运动情况与无量纲转动惯量较小时是类似的: 下落开始初期(t+=0～2), 平板在重力作用下向下运动, 运动产生的气动力和力矩指向左上和顺时针方向, 和重力共同作用下平板进一步左下运动并顺时针转动. 平板角度转为负值后(t+=2～9.6), 气动力和力矩方向随之改变, 使平板向左的水平速度和顺时针转动速度减小并逐渐反向为向右和逆时针. 由于平板转动惯量较大, 惯性作用明显, 气动力矩反向后经过了较长的时间后平板转动角度才逐渐减小, 气动力矩作用的滞后现象明显. 也正是因为上述原因, 平板转动角度再一次反向后, 由于气动力矩变化的作用滞后时间较长, 无法及时反映至平板转动角度, 导致平板转动角度增大至较大值后无法拉回, 在惯性作用主导下朝同一方向翻滚最终形成周期性翻滚下落运动. 因此, 当平板初始角度本身较大时, 如图13中初始角度为60°时, 自由下落初期过渡运动状态中就出现了初始角度较小时过渡状态后期发展出的现象: 在惯性作用主导下直接朝同一方向翻滚形成周期性翻滚下落运动.

当转动惯量很大、 惯性作用更加明显, 更难以在过渡下落阶段出现摆动运动. 当无量纲转动惯量增大至I+=5.0时, 如图15所示, 过渡下落阶段发生摆动运动的范围进一步缩小, 仅在初始角度≤30°时出现过渡的非规律性的摆动运动: 在u+-v+曲线上显示为不对称的“∞”形轨迹.

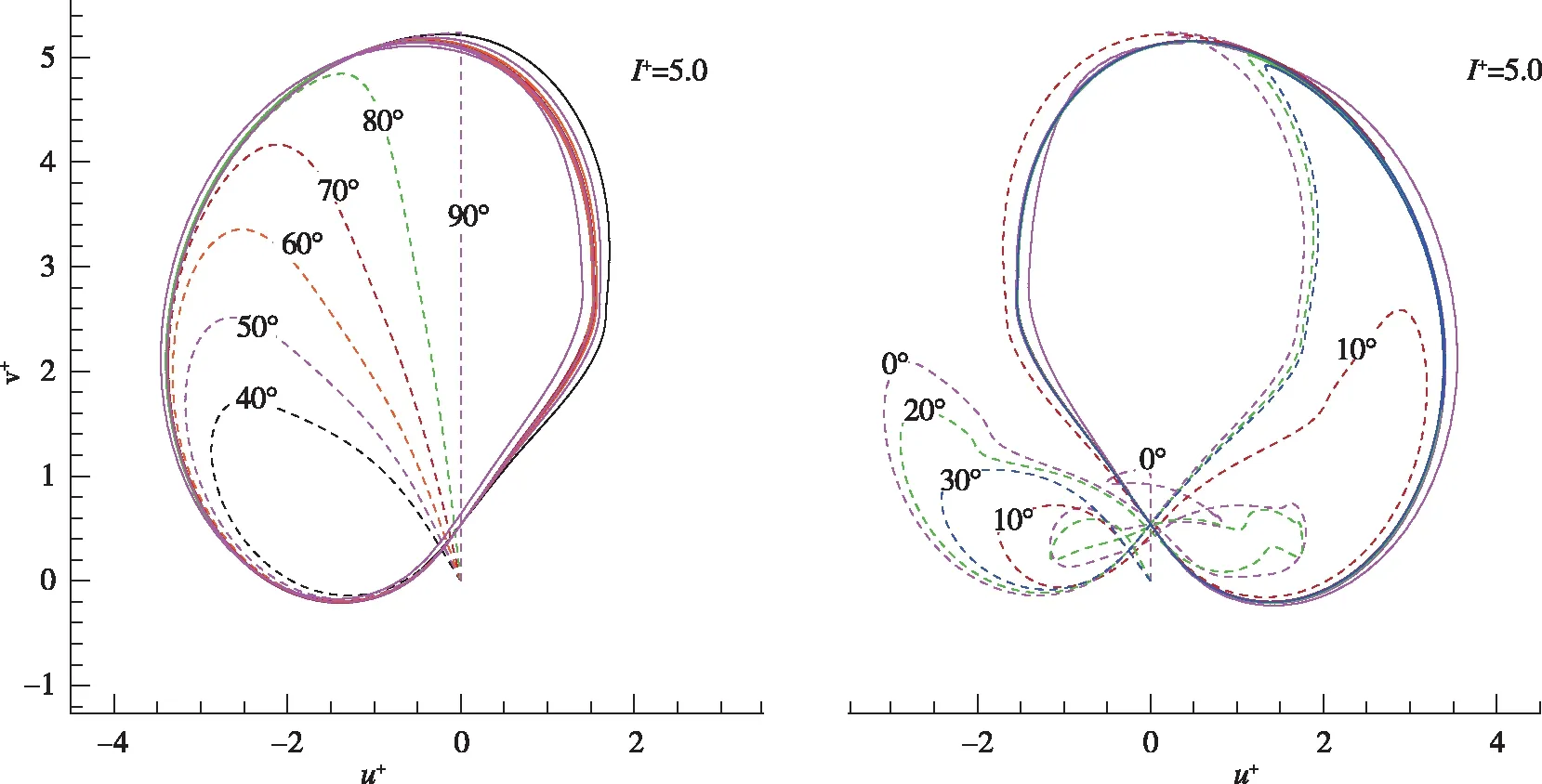
图15 u+-v+曲线(I+=5.0)Fig. 15 u+ versus v+(I+=5.0)

综上所述, 平板翻滚下落状态中过渡状态与周期性状态的机理是相似的: 由于平板转动惯量较大, 气动力矩仅能起到减缓或增大平板转动角速度的作用, 平板的转动角度方向不随气动力矩方向变化而改变. 因此平板大部分情况下保持了翻滚的运动状态. 仅在转动惯量稍小的情况下, 且初始角度较小、 处于临界状态附近时, 才会在过渡下落状态中出现少次的不规律摆动运动. 同理, 也解释了模拟结果: 影响平板下落最终运动状态的是转动惯量等关键性参数, 与初始角度无关.

4 结论

本文通过耦合求解N-S方程和运动方程, 从不同初始角度对平板自由下落状态和轨迹的影响出发, 开展了二维平板自由下落的非线性特征研究, 研究结果发现:

(1)初始角度对平板的自由下落运动状态和轨迹有影响, 但影响仅反映在自由下落初期2个周期内;

(2)不同初始角度造成平板自由下落初期运动不同的振荡状态、 振荡频率和幅值;

(3)平板的自由下落运动呈现两个阶段: 初期阶段、 后期阶段. 初期阶段运动形态不同, 后期阶段运动形态相同.