边坡稳定性分析及滑移面快速确定
2021-12-09叶帅华章瑞环袁中夏
叶帅华,章瑞环,袁中夏
(1.兰州理工大学 甘肃省土木工程防灾减灾重点实验室,甘肃 兰州 730050;2.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050)
0 引言
对于边坡稳定性的研究一直是岩土界广泛关注的问题之一。目前边坡稳定性的研究方法主要有有限元法和极限平衡法。针对有限元法[1-4],国内外学者做了大量工作,并取得了一定成果,但是仍有很多问题,例如:该方法着重边坡的变形分析,很难给出明确的临界滑移面[5];安全系数的力学概念不明确[6];当边坡变形较大时,容易出现计算不收敛等一系列问题。因此经典的极限平衡法[7-9]凭借其独特的优势在边坡稳定性分析中占据着主导地位,在国内外研究中方兴未艾。
极限平衡法在分析边坡稳定性时一般分两步进行:第一步,对某一可能滑移面,构造安全系数Fs与滑移面的关系;第二步,对众多潜在滑移面,计算安全系数并确定相应于最小安全系数Fs(min)的滑移面,即临界滑移面。近几十年来,绝大多数研究都集中到第一步,得出了许多有效的安全系数计算公式[10-12]:最早有Fellenius提出的瑞典条分法,后来有学者在此基础上又提出了Bishop法、Janbu法、Morgenster-Price法和Spencer法等。近年来,蒋斌松等[13]、郑宏等[14]基于极限平衡理论,采用无条分法给出了边坡安全系数的解析表达式;时卫民等[15]在假定滑裂面为平面的基础上,给出了阶梯型边坡临界滑移面及最小安全系数的解析算式。对第二步的研究,近年来也取得了许多成果,对边坡临界滑移面的搜索提出了一些新方法:如莫海鸿等[16]提出应用模式搜索法寻找临界滑移面;马忠政等[17]提出了三向搜索法,在一定程度上提高了滑移面搜索效率。目前临界滑移面的搜索方法主要有变分法[18]、固定模式搜索法、数学规划方法[19]、随机搜索方法[20]和人工智能方法等。但是无论哪种方法都没有摆脱广泛试算这一重大弊端,当自由度大时,其计算量将难以想象。另外,近年来可靠度理论也开始广泛运用于边坡稳定性分析中,并取得了颇为丰富的成果[21-22]。但现有的边坡可靠度分析大多建立在传统极限平衡条分法的基础上,自然而然地沿袭了传统极限平衡条分法的上述缺点[23]。
基于以上论述,在前人研究的基础上,本文拟提出一种采用解析的方法进行边坡稳定性分析及临界滑移面确定的新方法,并通过实例验证其可行性。此方法可提高边坡滑移面确定及稳定性分析的效率与精度,克服传统方法在边坡稳定性分析中存在的计算量大、滑移面搜索效率低等问题,为均匀土质边坡临界滑移面确定及稳定性分析提供技术参考。
1 基本假定
根据极限平衡理论和瑞典圆弧法的基本假设以及均匀土质边坡发生滑移时滑移面的位置、形状等基本特征,为方便滑移面控制方程和安全系数解析表达式的推导,提出以下3条基本假定:
(1)边坡为均匀土质边坡,其抗剪强度服从Mohr-Coulomb准则。
(2)土条间的作用力对边坡稳定性的影响不大,可以忽略;或土条两侧的作用力大小相等、方向相反且作用于同一直线上。
(3)假定剪切面为通过坡脚的圆弧面,即在横剖面上滑移面为圆弧;圆弧的圆心位于边坡上方。
2 滑移面确定模型
以边坡ABD为例,建立如图1所示的边坡滑移面确定模型。线段AB表示边坡坡面;BD表示边坡坡顶;β表示坡面角;H表示坡高。以坡脚A为原点建立直角坐标系0xy,圆弧AC为假定的滑移面,其圆心为点o,半径为r,圆弧AC与坡顶平面BD的交点为C;直线AE为圆弧AC在点A处的切线。根据建立的滑移面确定模型,进行滑移面控制方程的推导,具体过程如下。
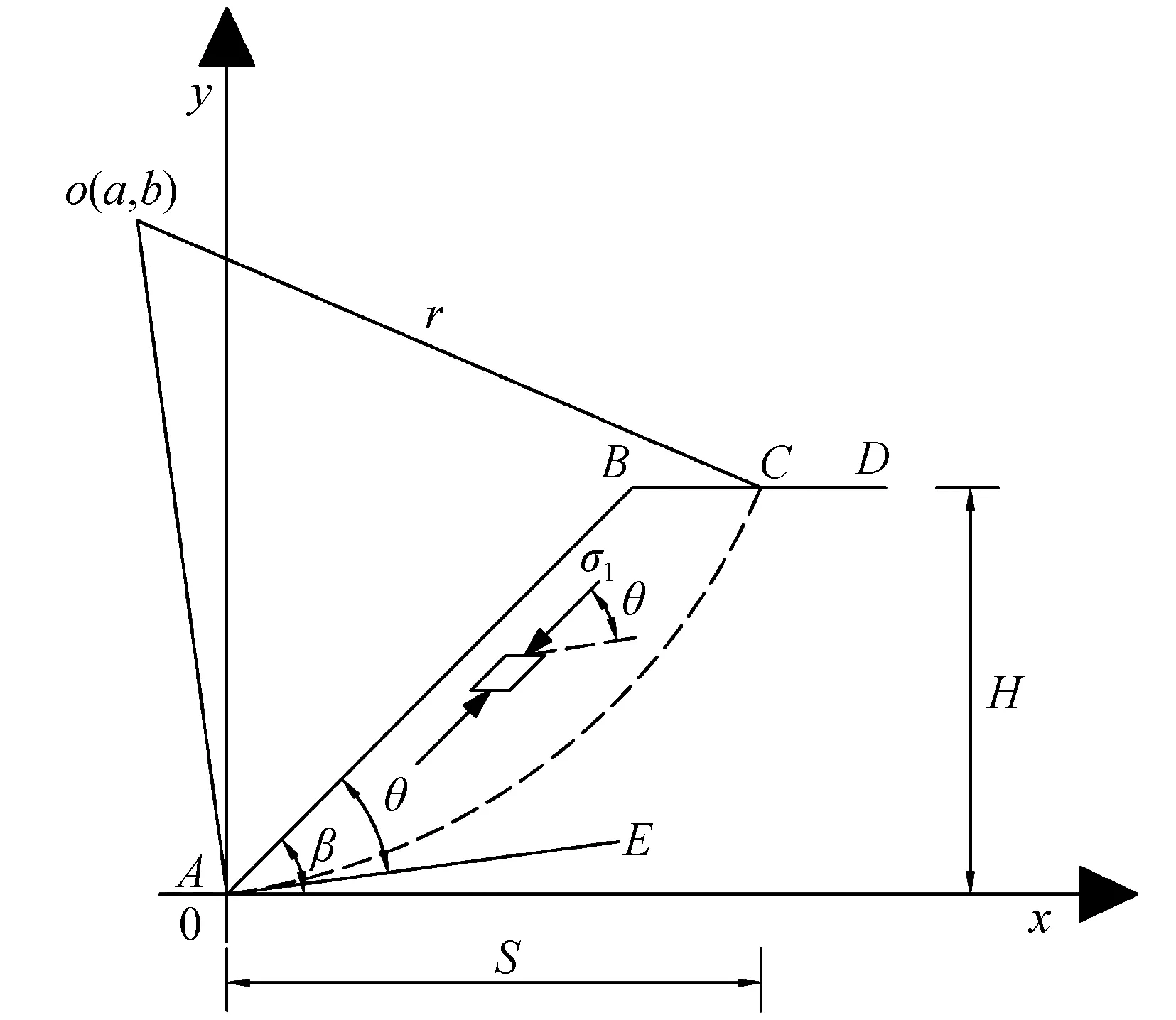
图1 边坡滑移面确定模型Fig.1 Determination model of slope slip surface
(1)在直角坐标系中,令点o坐标为(a,b),点C坐标为(S,H),点A坐标为(0,0),则圆弧AC的方程为:
(x-a)2+(y-b)2=r2
(1)
且满足:
a2+b2=r2
(2)
(S-a)2+(H-b)2=r2
(3)
(2)对于均匀土质边坡ABD,坡面AB处于单向应力状态,其上的作用力σ1为大主应力。根据Mohr-Coulomb破坏准则,当单元体剪应力达到土体抗剪强度时会发生破坏,那么滑移面AC与大主应力作用方向即坡面AB的夹角为:
(4)
令k为切线AE的斜率,由几何关系可得:
k=tan(β-θ)
(5)
则:
a=-kb
(6)
(3)联立式(2)、(3)、(6)可求得滑移面圆弧的圆心及半径表达式为:
(7)
式中:
(8)
至此,滑移面控制方程已确定。当一个边坡给定后,k、H均为已知量,滑移面控制方程将变成关于S的一元函数。
3 边坡稳定性分析
3.1 安全系数解析式推导
根据滑移面确定模型及控制方程,建立如图2所示的边坡稳定性分析模型,进行边坡安全系数解析式的推导。
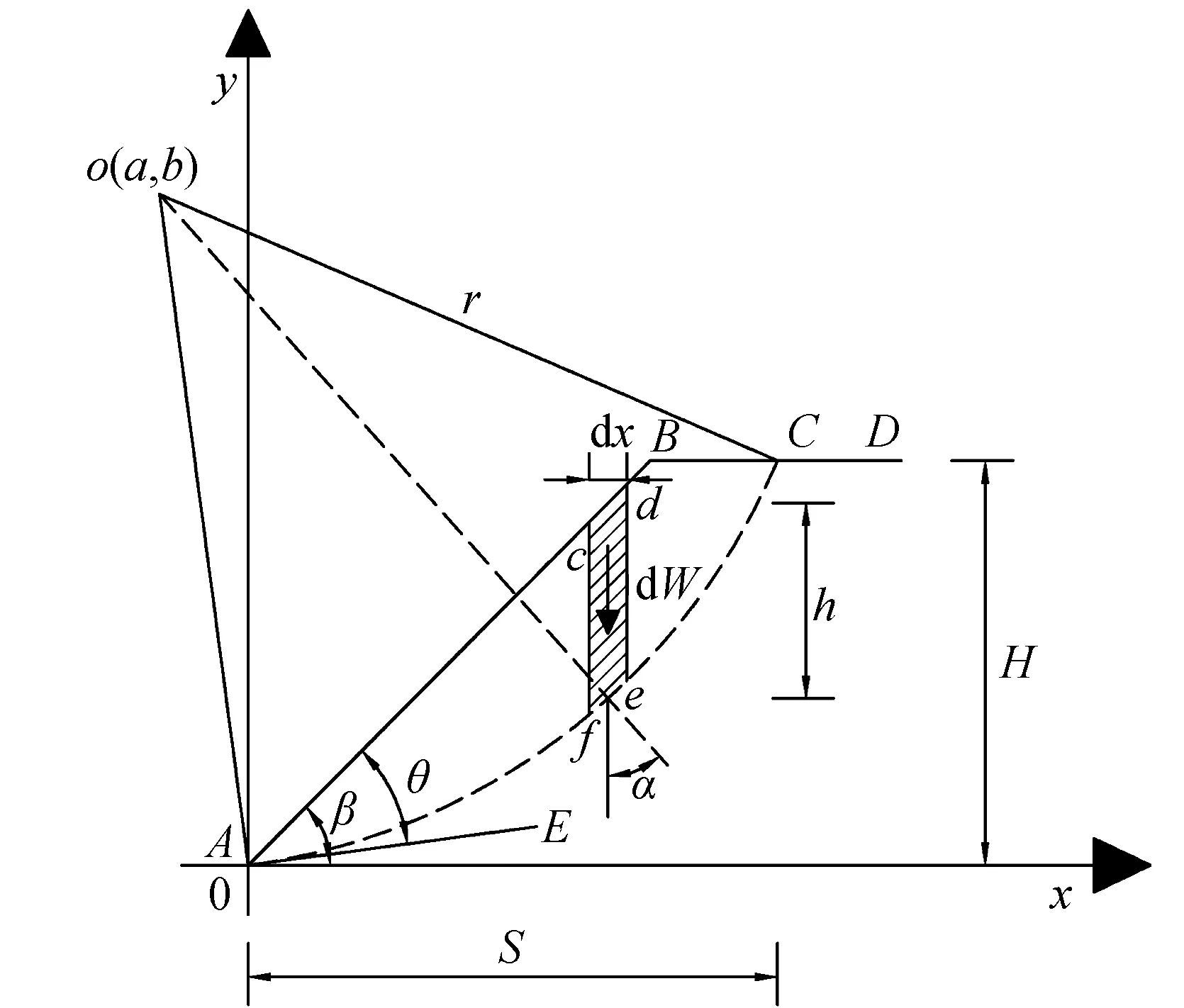
图2 边坡稳定性分析模型Fig.2 Slope stability analysis mode
将滑动土体ABCA划分为宽度dx趋于无限小的土条微元,取其中的土条cdef进行分析,其受力示意图如图3所示。该土条上的作用力有dW、dN及dT,由土条平衡条件得:
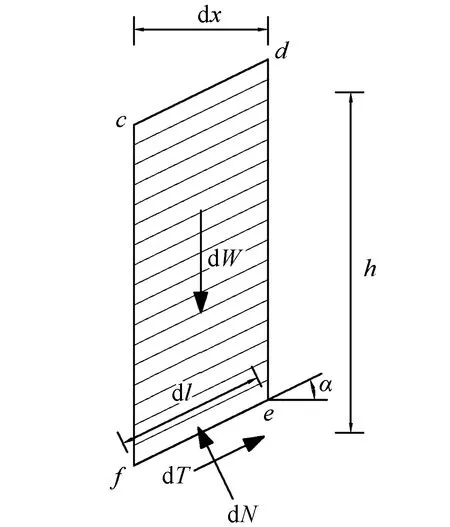
图3 土条cdef受力示意图Fig.3 Schematic diagram of the force on soil bar cdef
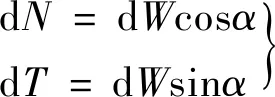
(9)
式中:dW=γhdx,为土条重力;dN为作用于滑移面的正应力;dT为作用于滑移面的剪应力。
由式(9)可得在整个滑移面上,由所用土条自重引起的剪力所产生的滑动力矩:
(10)
同理,由所有土条上的抗剪强度所产生的抗滑力矩为:
(11)
式中:xa、xb分别为积分下限与上限;c为土体黏聚力;φ为土体内摩擦角;l为弧长。
由几何关系可知式(10)、(11)中:
(12)
边坡的安全系数Fs为抗滑力矩Mr与滑动力矩Ms的比值:
(13)
式中:
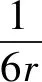
(14)
(15)
(16)
式中:a、b、r的取值列于式(7)。
3.2 临界滑移面和最小安全系数的确定
由式(13)可以看到,当一个边坡给定以后,边坡的安全系数Fs为S的一元函数,那么求最小安全系数Fs(min)将变为一元函数求最值的问题,亦为数学优化问题[24-25],其目标函数及约束条件分别为式(17)、(18)。
Fs(min)=minFs(S)
(17)
(18)
求解时可借助MATLAB计算软件,通过MATLAB中嵌套fmin函数实现对最小安全系数Fs(min)的求解计算,也可以应用图解法实现对Fs(min)的求解计算。求得S后,根据式(7)即可确定与最小安全系数Fs(min)相对应的滑移面,即临界滑移面。
4 算例验证
已知某均质边坡:坡高H=6.5 m,坡角β=55°,重度γ=19 kN/m3,黏聚力c=32 kP,内摩擦角φ=23°。对此边坡算例,采用不同方法进行临界滑移面的确定及最小安全系数计算,并对不同方法的计算结果进行对比分析。
4.1 本文方法
对上述边坡算例,采用本文方法进行边坡临界滑移面确定及最小安全系数计算。通过分析计算,在定义区间[4.6,31.9]内,S与Fs的关系如图4所示。从图4可以看到,当S=8.4 m时,安全系数Fs取最小值2.233,即最小安全系数Fs(min)=2.233。将S=8.4 m代入式(7)可以得到最小安全系数所对应的临界滑移面圆心坐标o(-2.396,11.774),半径r=12.015 m。
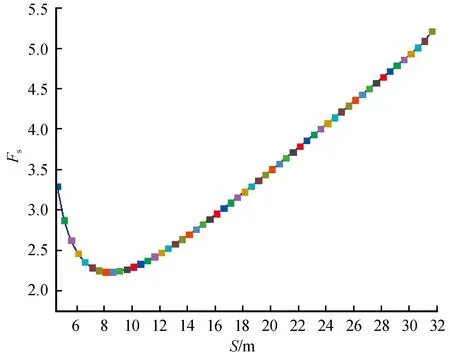
图4 S-Fs关系曲线Fig.4 S-Fs relation curve
4.2 传统极限平衡条分法
对上述边坡算例,采用基于传统极限平衡条分法的边坡稳定性分析软件GeoStudio中的SLOPE/W分析模块进行边坡稳定性分析计算,并选用Bishop法、Janbu法、M-P法和Spencer法4种不同的分析方法(统称传统极限平衡条分法),建立如图5所示的分析模型。各方法的计算结果列于表1。
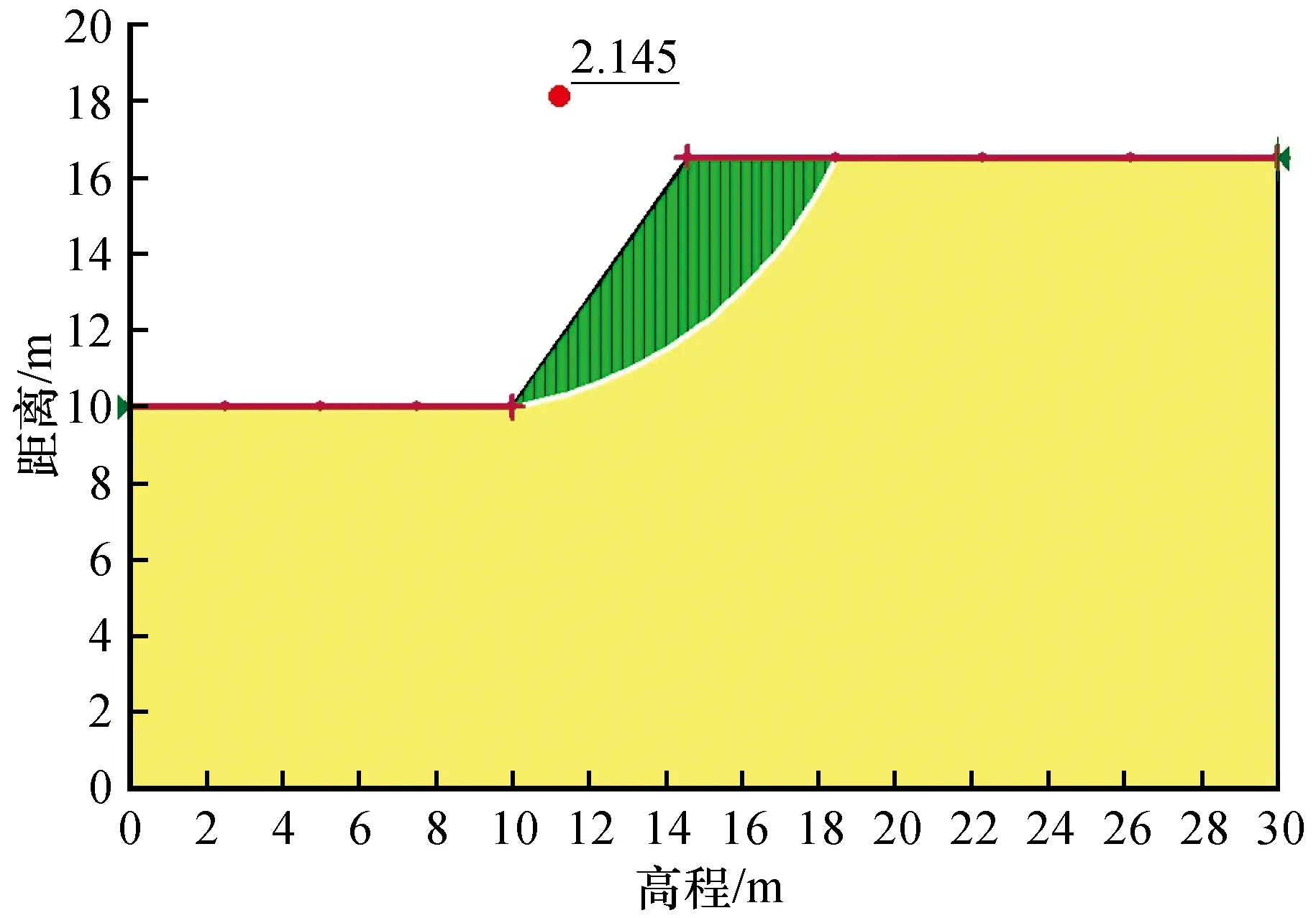
图5 GeoStudio边坡稳定性分析模型(Bishop法)Fig.5 GeoStudio slope stability analysis mode (Bishop method)
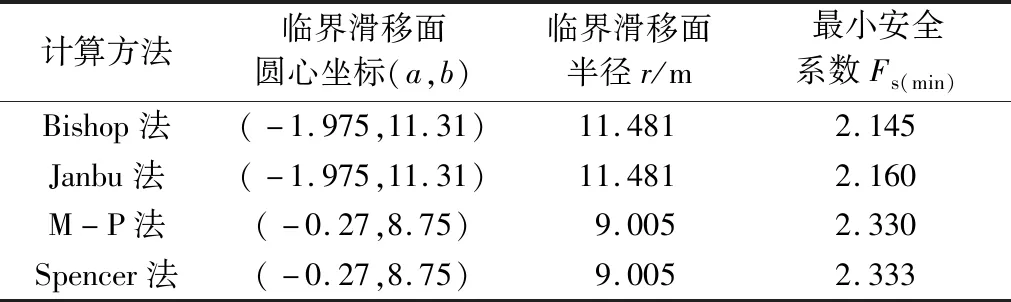
表1 传统极限平衡条分法边坡稳定性分析结果Table1 Analysis results of slope stability with traditional limit equilibrium methods
4.3 对比分析
将采用本文方法求得的边坡最小安全系数与采用传统极限平衡条分法求得的结果进行对比(表2)。从表2中可以看到,两种方法分析结果的定性完全一致(Fs(min)>1.0,边坡稳定),定量相近,最小安全系数相对偏差不超过±5%。将采用本文方法计算确定的临界滑移面与基于传统极限平衡条分法广泛搜索得到的临界滑移面进行对比,结果如图6所示。从图6可以看到,本文方法所确定的临界滑移面与基于Bishop法和Janbu法所广泛搜索的滑移面基本一致,而与基于M-P法和Spencer法所广泛搜索的滑移面有一定差异。其主要原因在于对条间力的考虑方面本文方法与Bishop法和Janbu法比较相似,与M-P法和Spencer法则差距较大。但整体而言,采用本文方法所确定的临界滑移面与基于传统极限平衡条分法所广泛搜索的滑移面还是比较接近的。
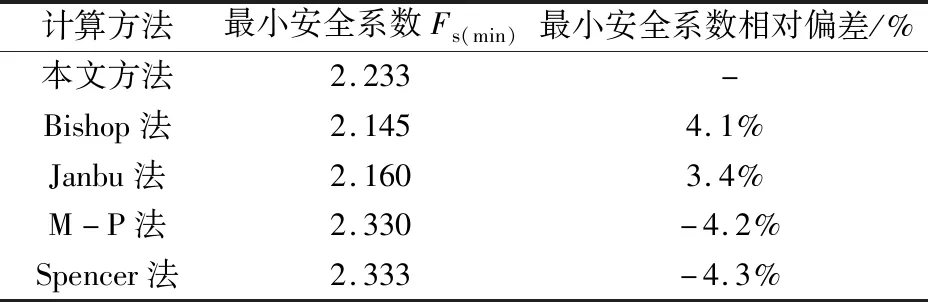
表2 安全系数对比Table 2 Comparison of safety factors
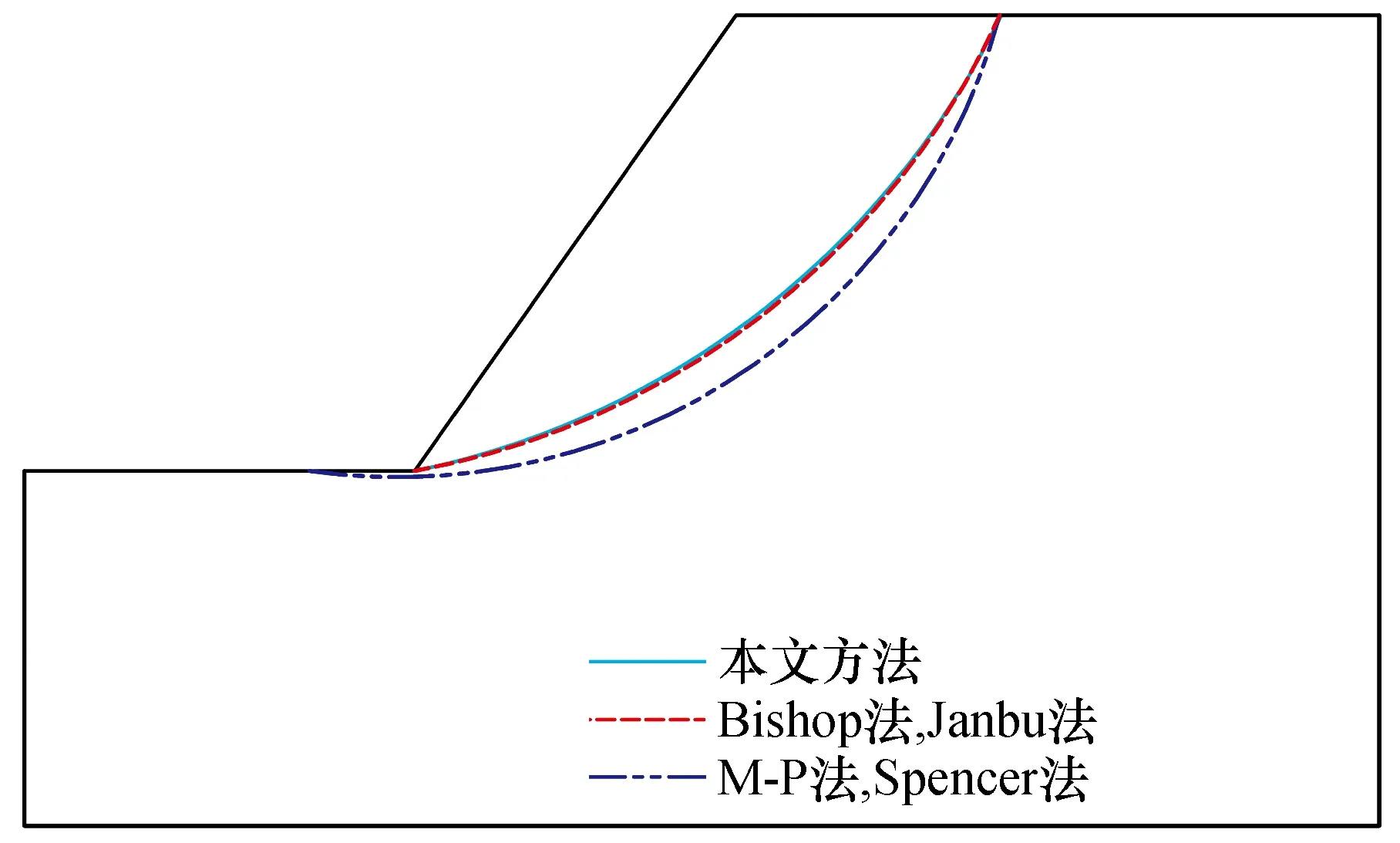
图6 不同方法搜索的临界滑移面示意图Fig.6 Schematic diagram of critical slip surface with different methods
该实例佐证了本文基本假设的合理性,也证明了本文方法在边坡稳定性分析及临界滑移面确定方面的可行性。相对GeoStudio而言,本文方法不需要划分网格,并进行广泛的搜索计算,也不会出现搜索计算不收敛的情况,所以在边坡稳定性分析方面具有较大的优势。
5 参数影响分析
本文方法的特殊之处就是引入了参数k,但参数k的合理性并不能通过一个算例来充分说明,还有待进一步验证。k的取值与坡面角β与土体内摩擦角φ有关。因此以上述算例为背景,针对β与φ分别设计单因素试验,采用本文方法和严格的M-P法进行稳定性分析计算,并将分析结果进行对比,研究参数β、φ对本文方法分析结果准确性的影响,同时研究其对边坡稳定性的影响。
5.1 参数β对本文方法准确性的影响
坡面角β取30°、45°和60°,采用本文方法和M-P法分别进行稳定性分析计算,结果如图7所示。图7中,RDmax代表最小安全系数相对偏差的最大值。从图7中可以看到,本文方法的准确性不受β取值影响,始终与M-P法的计算结果保持较高的相似性,偏差最大时仅为1.8%。边坡稳定性受坡面角β的影响明显,最小安全系数Fs(min)与坡面角β基本呈反比例关系。
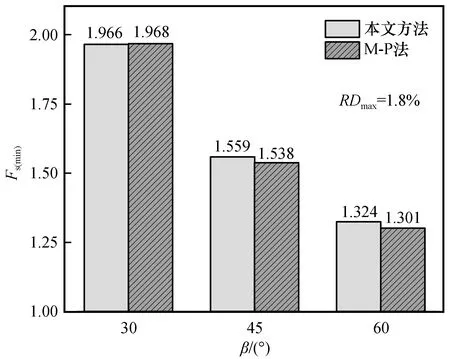
图7 参数β对本文方法准确性的影响Fig.7 Influence of parameter β on the accuracy of the proposed method
5.2 参数φ对本文方法准确性的影响
土体内摩擦角φ取16°、22°和28°,采用本文方法和M-P法分别进行稳定性分析计算,结果如图8所示。从图8中可以看到,本文方法的准确性也不受φ取值影响,始终与M-P法的计算结果保持较高的相似性,偏差最大时仅为-1.5%。边坡最小安全系数Fs(min)与φ呈正比例关系。
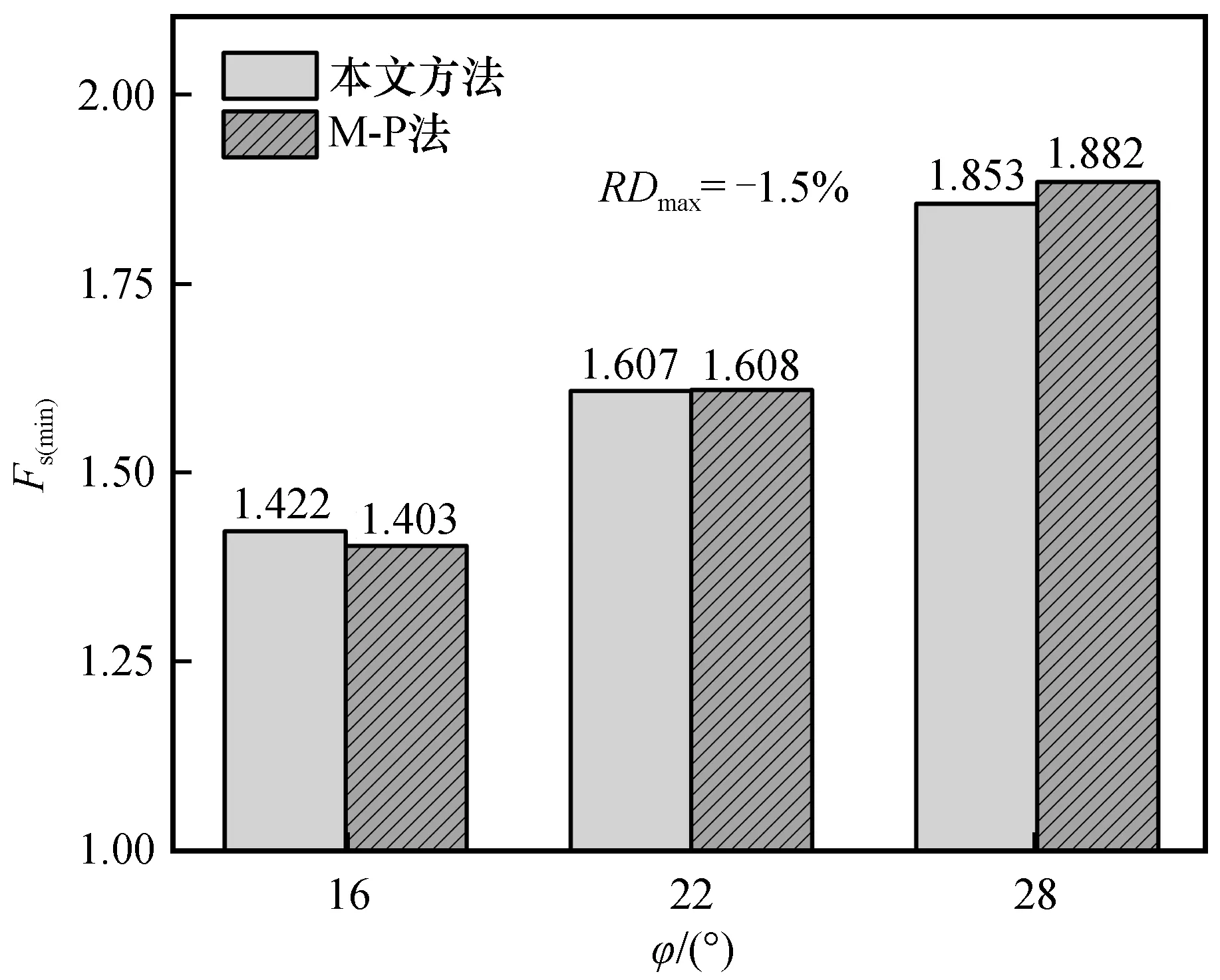
图8 参数φ对本文方法准确性的影响Fig.8 Influence of parameter φ on the accuracy of the proposed method
通过上述分析可以看到,本文方法边坡稳定性分析结果的准确性不受边坡参数取值的影响,始终与M-P法的分析结果保持较高的相似性,这也说明本文方法中参数k的取值是科学、合理的。
6 结论
本文基于极限平衡理论,提出一种边坡稳定性分析及滑移面快速确定的新方法,并通过算例及试验对该方法进行了验证,得到以下结论:
(1)本文方法边坡稳定性分析结果与传统极限平衡条分法分析结果的定性一致,定量相近,二者分析得到的最小安全系数的相对偏差不超过±5%,完全满足工程要求。
(2)本文方法所快速确定的临界滑移面与基于传统极限平衡条分法所广泛搜索的临界滑移面比较接近。
(3)本文方法边坡稳定性分析结果的准确性不受边坡参数取值的影响,始终与传统极限平衡条分法保持较高的相似性。
