基于忆阻器神经网络和改进Logistic映射的图像加密法研究
2021-12-09李涵,葛斌
李 涵,葛 斌
随着计算机网络技术的发展,图像作为一种信息载体被广泛使用.但由于图像信息量大、冗余度高的特点,传统的加密算法,如DES(Data Encryption Standard)等对文本进行加密的算法[1],已经不适用于对图像进行加密.由于混沌映射函数具有对初值敏感性、伪随机性、非周期性等特点,被广泛应用到随机序列的生成,这使得混沌加密算法受到众多学者的关注[2-10].
混沌映射包括:低维映射与高维映射,其中,一维Logistic混沌映射函数,形式简单且运算效率高,被广泛使用[3],但其安全性较低;高维映射参数多,安全性高,但其效率较低[4];因此,一些学者通过改进一维混沌映射,提高混沌序列的随机性[5-7].周辉等[6]通过构造2维Henon-Sine映射,提高混沌映射函数的性能.对于加密系统而言,混沌序列应用到置换与扩散操作中,增强了混沌序列的随机性,加密系统的安全性也随之提高.
对于图像加密算法而言,像素级的置乱操作仅仅能改变像素的位置,破坏相邻像素之间的相关性,但是每个像素值在整张图像中出现的频率并没有改变.因此,像素级的置乱操作不能抵抗统计分析攻击.而对图像中像素进行bit位置乱操作却能够同时改变像素值的位置和大小,算法效率较高,能够达到抵抗统计攻击的目的[9-10].
本文选择忆阻器神经网络,将其更新的权值作为混沌系统的密钥,使用生成的混沌随机序列完成图像的置乱和扩散;并通过密钥空间分析、信息熵分析、直方图分析、相关性分析等进行安全性分析.
1 复合指数混沌系统
通过引入指数函数ek,对1-D Logistic映射进行改进,xk为1-D Logistic映射,复合指数混沌系统yk定义为:

其中:μϵ[1,4],步长为10-3,对原混沌映射函数进行改进后,其混沌特性明显增强.由图1可以观察到其混沌范围变广;当参数μ>2.7时,函数已完全进入混沌状态,且没有周期加倍的分岔现象.

图1 复合指数混沌系统
1.1 自相关性分析
本文所考虑的自相关性是指混沌系统在经过步长为d而产生序列长度为L的迭代过程中,一个步长的取值与另一步长取值的依赖关系,其公式可以表示为:
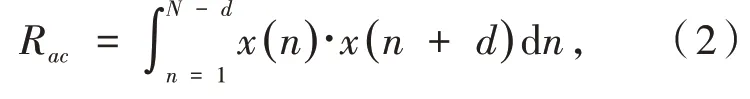
其中:Rac为自相关系数,x(n)为序列值.
输入初始值x0=0.2,μ=4到混沌系统,对获得的长度为65 536的混沌随机序列x1进行分析.从图2可以看出,随机序列在滞留间隔内只有一个最高峰,且相关性在x轴上下波动,相关性系数接近于0.

图2 随机序列自相关性
1.2 Lyapunov指数
Lyapunov指数是识别混沌运动的一个重要数值特征,当出现数值为正数时,系统则产生混沌现象.由于在一维混沌映射中,其仿真数值并不是很理想.
本文提出的混沌系统则表现出较好的混沌特性.从图3可以观察到,混沌系统的Lyapunov指数皆为正值,表示其具有良好的混沌特性.
1.3 NIST检验
NIST SP 800-22 Test Suite为随机性检测工具,其中介绍了15种检测随机性的统计学方法.本文使用随机性检验套件对混沌随机序列进行测试,为满足NIST检验的15项测试要求,首先对1 000 000个混沌序列值进行二值化处理,然后对取得的1 000 000位二进制序列进行NIST检验.
对于15项随机性检验,每一项都会产生[0,1]的P值,当P值大于显著性水平(α=0.01)时,则表示二进制序列通过测试且满足随机性特点.通过表1可以观察到,所取得的随机序列通过了NIST随机性检验,混沌序列具有良好的随机特性.
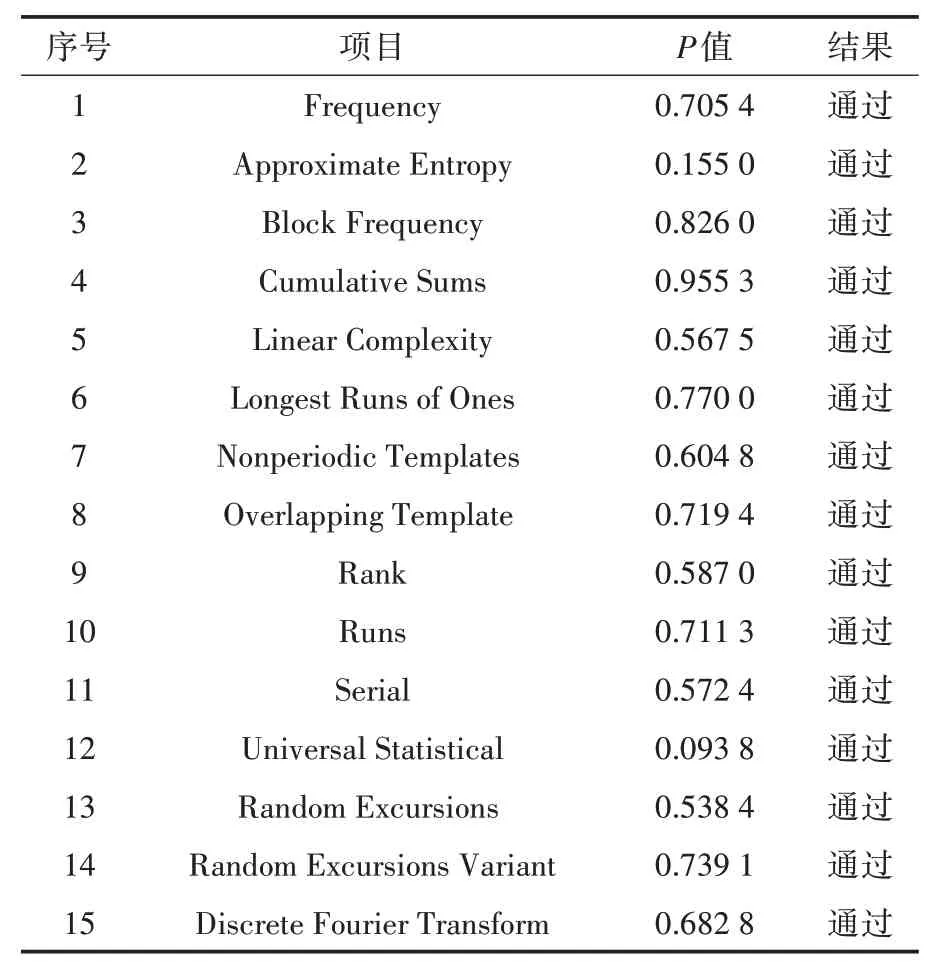
表1 NIST检验
2 忆阻器神经网络
2.1 忆阻器
忆阻器模型是由两层铂触点和两层TiO2薄膜组成,其中一层由于氧空位的掺杂而起到半导体的作用,而另一层则是显示出绝缘性能,掺杂区的宽度可由通过忆阻器的电荷来确定.由于外界的激发,掺杂区的氧空位出现了漂移,使区域之间的边界向同一方向移动[11].
在描述边界偏移速率时,同时考虑到忆阻器内部,以及边界条件的漂移行为使离子产生非线性状态,选择经典的Joglekar窗口函数对掺杂漂移行为进行建模;在文献[8]中,当p=1时,忆阻器的非线性特性最强,则非线性窗口函数f(x)表示为:

忆阻器阻值M(t)为:
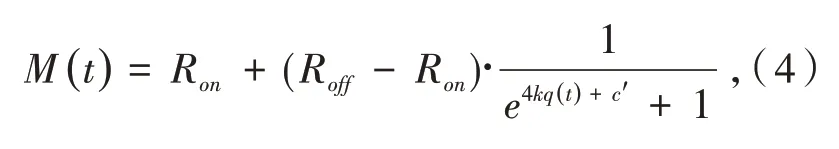
其中:Ron和Roff分别指忆阻器的低、高电阻,q(t)为流过忆阻器的电流,为参数,,μv为平均迁移率,约为10-14m2s-1V-1.
由于忆阻器电导为其阻值的倒数,则忆阻器电导G(t)为:
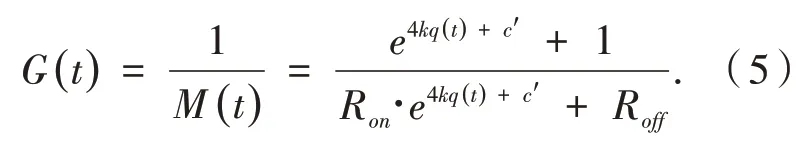
忆阻器电导对时间t进行微分,可得到关于电导变化率的方程为:
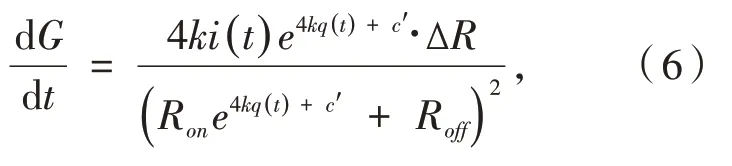
2.2 基于忆阻器的神经网络
由于混沌多项式的递归和正交特性,被选择作为神经网络的激活函数,本文选择Che⁃byshevⅡ类多项式作为神经网络的激活函数.
神经网络的输出.本文选择ChebyshevⅡ正交多项式作为全连接层神经网络的激活函数,x为输入,wi为权值,Ci(t)为激活函数,则输出层y为:
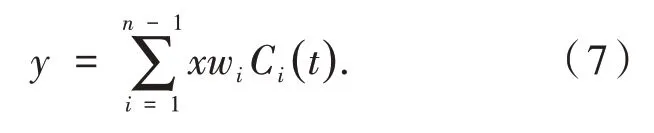
计算误差:

其中:f(x)为期望输出,y为实际输出.
权值更新.使用忆阻器电导率∆G代替∆w,当电流很小时,忆阻器电导的变化也很小,趋近于0;当电流值为±4 mA时,忆阻器电导会产生很大的变化,由忆阻方程推导出的权值更新方程为:
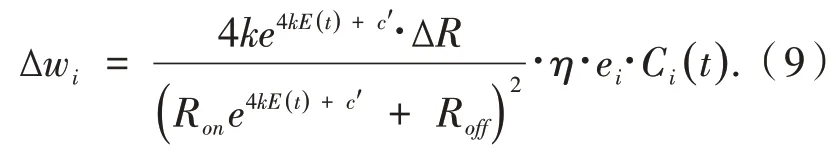
利用误差ei代替为ei的积分,η为学习率,Ci为Chebyshev混沌多项式.
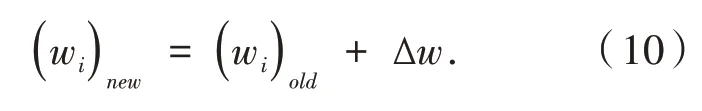
计算所得的权值作为加密过程中的密钥,且加密解密都使用同一个神经网络,如图4所示.
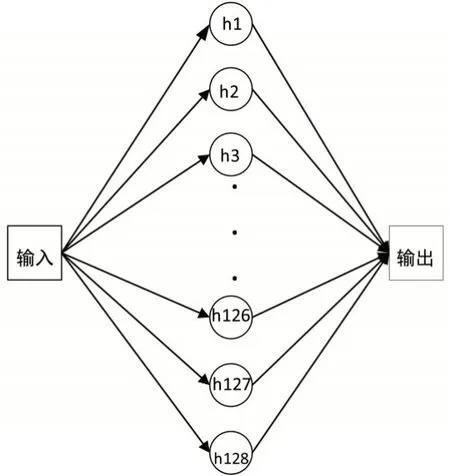
图4 神经网络
3 加解密算法
3.1 加密算法
STEP1:初始值密钥的选取.将明文像素矩阵连同在明文像素矩阵中随机选取的像素值x作为混沌神经网络的输入,设置输入层和隐层之间的权值为1,混沌神经网络一经确定输入值和权值,便向输出快速收敛并进行权值的更新.将混沌神经网络得到的权值wi作为混沌系统的密钥值,其中算法1为混沌系统初始值,以及控制参数的更新算法.

STEP2:混沌序列的生成.使用算法1获得混沌系统的初始值与控制参数x1,0、μ1,进行N0+l次的迭代后,为避免暂态效应,省略掉前面的N0个值而保留后面的l个值,生成混沌序列S={s1,s2,s3,…,sl},其中l=M×N,M为明文像素矩阵的行,N为明文像素矩阵的列.
STEP3:获得索引数组,完成像素级置乱.将混沌序列S={s1,s2,s3,…,sl}转置为M×N混沌矩阵后,对其进行逐行逐列的排序,得到索引矩阵D;按照索引矩阵D对明文像素矩阵P进行置乱操作,得到置乱后像素矩阵P′.
STEP4:初始值选择.同样使用算法1获得混沌系统的初始值与控制参数x2,0、μ2,分别进行N0+8L次的迭代,将产生的混沌序列组合成序列W={w1,w2,…,w8L}.
STEP5:bit位重组.将P′中每个像素值转化成二进制的形式Q,如Q(1,1)={1 0 000 001};将混沌序列W转置为M×8N的矩阵,对其进行排序后,得到索引数组C;按照索引数组C对序列Q中的元素进行重新排列,组合成新的序列A,即为bit位置乱后的序列.
STEP6:密钥序列.首先,使用算法1获得混沌系统的初始值与控制参数x3,0、μ3,x4,0、μ4,进行N0+l次的迭代后,获得混沌随机序列S1和S2;从置乱后图像中随机选取像素值Ak,并在权值中选择wk1、wk2加入到混沌随机序列S1和S2中,使得混沌序列的长度为l+1.为满足扩散阶段的bit-wise异或,以及mod运算的要求,使用算法2分别对混沌随机序列S1和S2进行处理.

本文在进行bit位异或运算过程中,引入前一阶段的像素值,使得每一个值扩散都与前一个步骤相关,且与前一个密文像素点相关,实现密文反馈机制,增强了加密算法的安全性.
STEP7:扩散.第一轮:在扩散加密时,引入bit级置乱后的结果A(l),作为扩散的输入.
当l=1时,
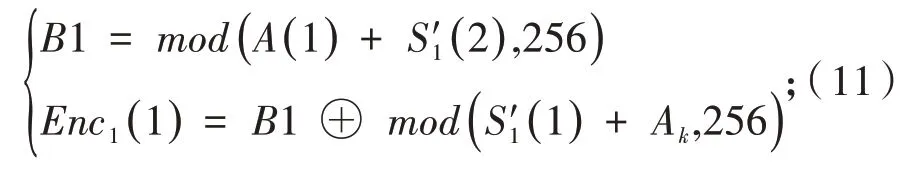
当1 第二轮:在扩散加密时,引入第一扩散后的结果Enc1(l),作为扩散的输入. 当l=L时, 当1≤l 得到最终的加密图像为Enc2. 解密算法为加密算法的逆运算,且解密过程中所使用的密钥与加密过程中所使用的密钥相同. 图5为图像加密前后的对比,加密算法已经完全改变了图像原本的特征,安全性较高.下文将从抗统计攻击、信息熵、相邻像素相关性等方面对加密结果进行分析. 图5 图像加密结果 密钥作为明文和密文之间相互转化的参数,其空间的大小是衡量加密效果的重要指标,密钥位数越长,其密钥空间越大;本文密钥精度可以达到10-15,其密钥集合E={x1,0,μ1,x2,0,μ2,x3,0,μ3,x4,0,μ4,Ak,wk1,wk2,N0};因此,密钥空 间 为(1015×8)×256×256×256×3 000≈2435,其密钥空间≫2128,能够抵抗穷举式攻击. 对于一张有完整意义的图像,其相邻像素之间必定存在较强的相关性,因此第三方可以通过对图像像素值进行统计分析,实现统计攻击. 4.3.1 相邻像素相关性分析 在加密算法中,通过对原图像的像素进行置乱操作,破坏了原图像相邻像素之间的相关性,进而达到了抵抗统计攻击的目的.在对图像进行相邻像素相关性分析时,分别从原图像与密文图像中随机选择5 000对像素点,从水平、垂直及对角线三个方向,对像素点相邻像素相关性进行计算,计算公式为: 由图6可以明显地观察到加密前,图像相邻像素之间的相关性近似为1;由表2可知,加密后其相关性几乎为0,完全破坏了图像相邻像素之间的相关性,原图像变得毫无意义. 表2 相邻像素相关性 4.3.2 直方图分析 直方图是对图像中像素出现频率进行统计的工具;图7中,加密前,可以清楚地观察到原图像中每一个像素值占整张图像像素个数的比例,而加密后的直方图,每一个像素的分布都变得均匀,达到了抵抗统计攻击的目的. 对信息源的不确定度的度量,是图像所包含信息的重要指标.信息熵越大,则图像所包含信息越多,其混乱程度越高,因此,也不容易被第三方获得图像所包含的信息.加密后信息熵的理想值为8.信息熵的数学公式为: 图6 相邻像素相关性分析 图7 直方图分析 表3为对不同图像加密后的信息熵,从表中可以观察到加密后的图像信息熵为7.997 3,接近于8,加密算法不易被第三方获取信息. 表3 信息熵 本文通过引入指数函数,对一维Logistic混沌映射进行改进,提出一种基于忆阻器神经网络与改进Logistic混沌映射的图像加密算法,仿真实验证明提出的混沌映射的随机性明显提高;忆阻器神经网络的应用,为加密系统的密钥提供了选择;并且神经网络的输入与明文相关,使得混沌系统的初始值与明文相关,达到了一次一密的Shannon完善保密性标准;双重置乱算法使得加密结果能够抵抗统计分析攻击;双向扩散算法使得每一个像素的影响扩散到整张图像,加密算法的安全性提高,能够抵抗典型的攻击.

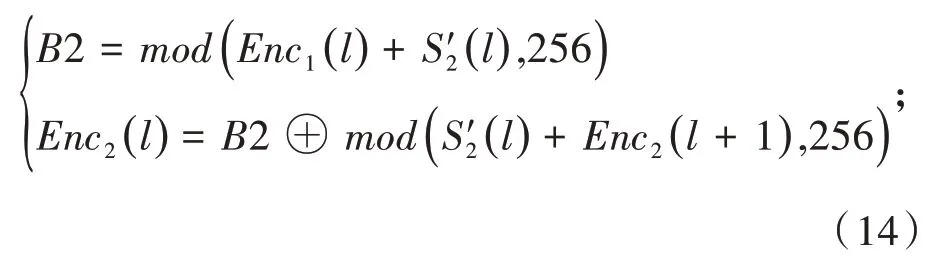
3.2 解密算法
4 实验结果与安全性分析
4.1 加密结果

4.2 密钥空间
4.3 统计攻击分析
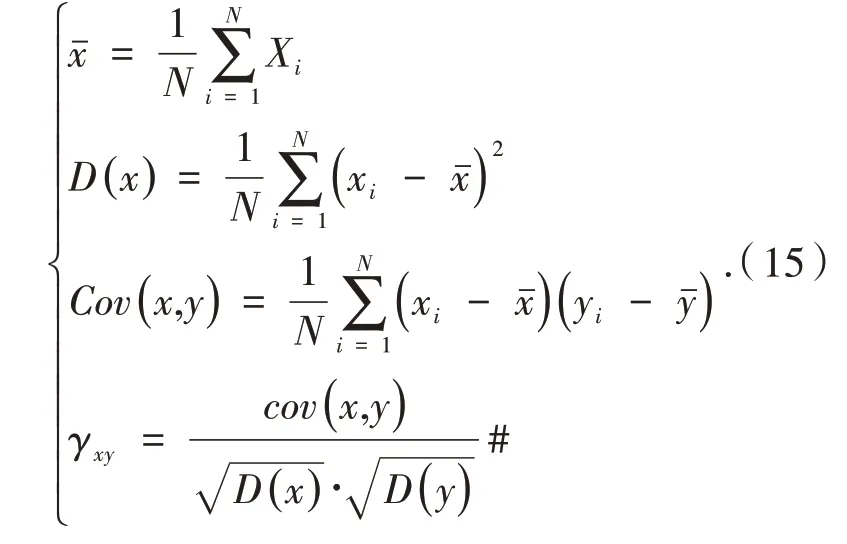
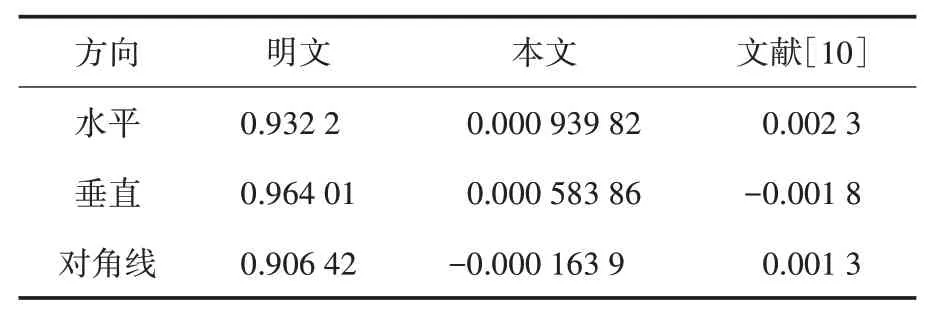
4.4 信息熵分析


5 结语
