情境视角下的习题比较及价值分析

【摘 要】近年来，数学情境问题备受关注，是数学教育研究的重要议题.以人教版和北师大版的初中数学教材为研究对象，对教材中“一次函数”章节的习题情境进行比较分析，发现：在情境类型上，两版本主要以无情境和个人情境为主，忽视职业情境和社会情境.在情境水平上，两版本各有特色.在数学特征方面，北师大版的运算要求高于人教版;在表征特征上，人教版较少直接运用图形表格这样直观的表征，北师大版表征方式更为丰富多样;在任务特征上，两版本都注重概念性理解，人教版以基础性巩固和常规性运用为主，北师大版则更注重问题解决和问题探究.通过对个别经典案例进一步分析，发现人教版善于联系生活实际，北师大版忠于学科间横向联系.

【关键词】数学教科书;习题;情境;一次函数;比较研究

1 研究背景

数学教科书作为数学教学过程中重要的工具，由正文、例题和习题三部分有机组成.不同层次的例题和习题，是加深数学概念、命题及定理的理解，深化数学基本思想、数学方法及技能的掌握和数学活动经验的积累，是教科书的重要组成部分[1].习题包括教科书中的练习、习题和复习题，是帮助学生理解和巩固新知识，提高应用新知识分析和解决问题技能的重要载体.近年来，关于习题的研究有很多：鲍建生为寻找习题比较的量化标准，建立了综合难度的一个多因素模型，为习题比较提供了工具[2];以二次方程及函数为例，高文君和鲍建生设计了数学认知水平分析框架，发现中美习题在不同认知水平上的差异[3];贾随军、吕世虎和李保臻从习题的数量、类型及难度方面分析了中美“与三角形有关的角”的习题[4].习题的质量影响着数学知识内容的表征程度和渗透程度，对数学教学也有着深刻的影响.问题是数学的心脏，数学问题离不开数学情境.通过梳理文献发现，关于习题在问题情境方面的比较研究较少.

数学情境在数学教学中发挥着关键的作用.《义务教育数学课程标准（2011年版）》（以下简称《课标（2011版）》）提出：“数学课程能为学生未来生活、工作和学习奠定重要的基础;课程内容的选择要贴近学生的实际，有利于学生体验与理解、思考与探索.”习题以问题的形式表现，为学生内化数学知识，获得数学技能、丰富数学活动经验所服务.基于此，研究以“数与代数”板块中的“一次函数”章节为依托，对国内不同版本的教科书习题情境进行比较，深度挖掘习题价值所在，以期对函数习题的设计提供借鉴与启示.

2 研究设计

2.1 研究对象

本研究选取人民教育出版社、北京师范大学出版社出版的义务教育教科书《数学》（以下分别简称“人教版”“北师大版”）“一次函数”章节的习题，其内容如下表1.

2.2 分析框架

2.2.1 数学问题情境类型

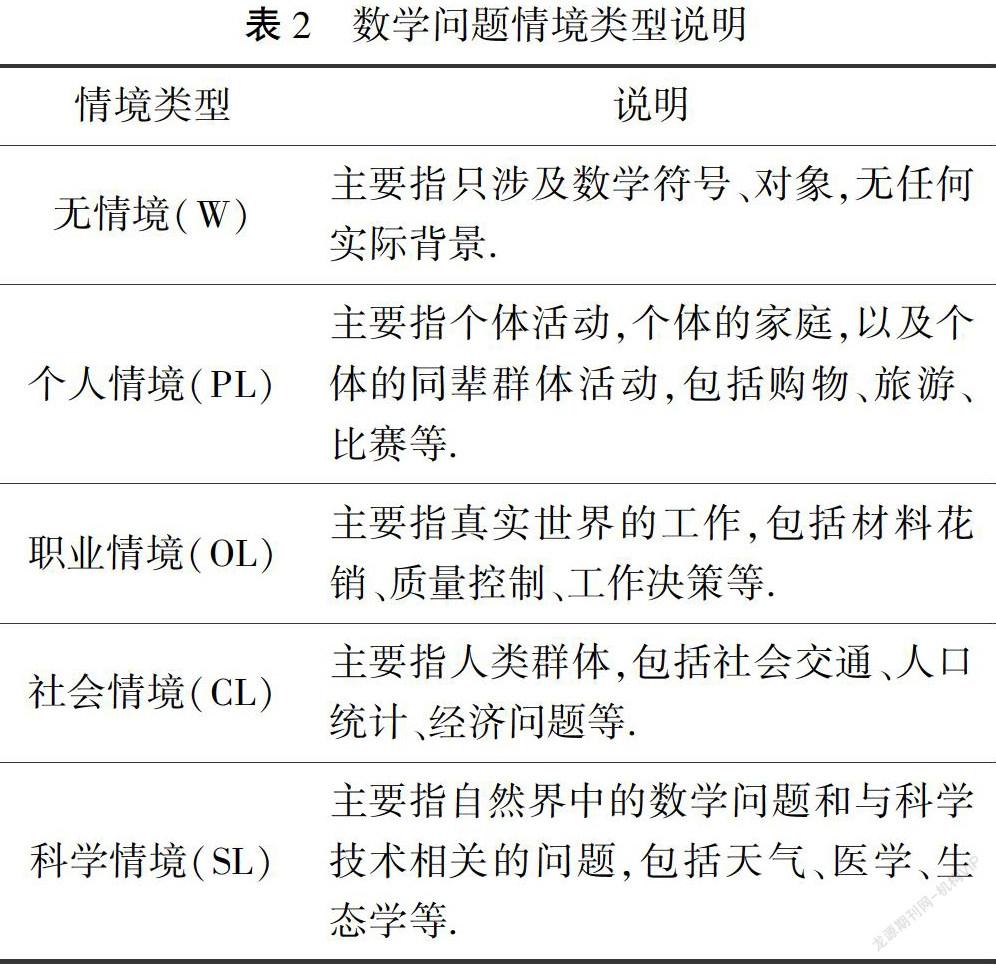
根据PISA中情境的分类方式，按照“情境与学生生活远近程度”，将问题情境划分为个人情境、职业情境、社会情境和科学情境.结合数学问题呈现的简洁性，将“无情境”也作为一种情境类型，从而将数学问题情境划分为以下5类（见表2）.

2.2.2 數学问题情境水平

数学情境是关于“学习活动的环境”及“数学学科知识”的整合，在数学问题情境中包含相关的数学知识与数学思想方法.Yeping Li开发了一个针对教科书数学问题呈现的3维度分析框架，即“数学特征”、“表征形式”和“任务要求”，鲍建生在习题综合难度模型中提出探究、背景、运算、推理和知识含量5个因素.根据数学问题呈现的维度，结合习题综合难度模型中考虑的因素，以陈志辉改进的数学问题情境水平分析框架为工具，得到“数学特征水平”、“表征形式水平”及“任务特征水平”三维特征分析模型，见表3.

以人教版中的一道习题为例：甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾，其中甲商场所有商品按8折出售，乙商场对一次购物中超过200元后的价格部分打7折.

（1）以x（单位：元）表示商品原价，y（单位：元）表示购物金额，分别就两家商场的让利方式写出y关于x的函数解析式;

（2）在同一直角坐标系中画出（1）中函数的图象;

（3）春节期间如何选择这两家商场去购物更省钱？

根据上述分析框架，首先在情境类型上，商场购物属于个人情境，其次，对该问题情境从三个维度分析：数学特征上，该问题的外部表征并没有包含运算，因此属于水平1（NC1）;表征特征上，该问题是将商场购物的背景以文字描述出来，且不含任何图表，属于水平2（S2）;任务特征方面，此问题是利用一次函数来解决购物问题，因此将其归为水平3（PS3）.

3 研究结果

根据以上分析框架对两个版本相应的内容进行统计和分析，得到以下研究结果.

3.1 数学问题情境类型比较结果

通过统计人教版和北师大版“一次函数”习题，发现人教版共65道，北师大版共57道，人教版习题数量更多.由表4及图1知，人教版和北师大版在习题情境类型的侧重上有相似之处，其中，无情境和个人情境的习题数占总数的80%以上，而有关职业情境和社会情境的习题都不足10%，说明两个版本对于“一次函数”情境都着重于学生日常生活经验，忽视了学生未来生活发展的职业情境以及社会情境.

根据两个版本情境类占比情况，得到图2.可见人教版教材和北师大版教材习题设置的一致性.对人教版和北师大版问题情境各类型进行横向比较，发现两版本情境类型分布在整体相似的基础上，人教版无情境习题比个人情境习题多7.7%，相应地，北师大版相差14%，说明北师大版更注重无情境习题设置.此外，人教版个人情境和科学情境较北师大版多，而北师大版在公共情境和职业情境上，设置比人教版更丰富.

3.2 数学问题情境水平比较结果

3.2.1 数学问题情境整体水平比较

根据三维特征分析模型，对两版教材中的习题进行统计，每一个维度不同水平赋予不同分值，为确保习题在各水平划分上的客观性，统计前制定一个合理的评判规则，在统计过程中按照制定的评判规则，采用多人多次评分的方法，对有争议的数学问题进行讨论和意见整合，从而得到表5，即不同版本习题各维度在不同水平层次上的分布频数，通过计算不同版本三个特征的均值，同时绘制折线图，得到图3.

由图3可知，人教版和北师大版教材中“一次函数”习题问题情境总体水平有差异.总体来说，北师大版在各维度水平都高于人教版，且北师大版在三个维度上问题情境水平相差不多，而人教版在表征特征这一方面的值明显低于其他两个维度的值.

纵向来看，人教版教材中，其任务特征值（2.3692）和数学特征值（2.1692）较高，表征特征值最小;北师大版教材以任务特征值（2.5263）最突出，且在三个特征上表现水平基本持平.此外，人教版习题表征特征值较低，数学问题大多以纯数字或是文字这样的文本形式描述，描述形式不够丰富，相比之下北师大版习题中有很多问题以图文结合的形式表现出来.

3.2.2 数学问题情境各特征水平比较

（1）数学特征

从整体来看，两版本有一定的相似之处，但存在细微差别，故对人教版和北师大版教材数学问题情境在各特征方面表现作进一步分析，探究各维度的相同点与差异处.

由图4可知，人教版和北师大版教材“一次函数”数学问题都主要以无运算、一步运算、两步运算居大多数，三步运算以上的数学问题仅占了少部分;对比人教版和北师大版各比重分布，发现人教版中含三步以上运算问题所占比例不及北师大高.

结合“一次函数”内容分析，人教版和北师大版都以变量引入函数，而理解变量及变量间的关系是学习函数知识的关键，因此两个版本在此节设置的都是无运算的数学问题，基于“一次函数”中对概念的理解会涉及求函数解析式、求某个点的坐标、解决实际应用题等，两版本在后续设置了不同运算长度的数学问题.

（2）表征特征

图5是对两个版本“一次函数”数学问题情境的表征方式做了對比分析，可以看出人教版以纯数字或短语占据绝大多数，其次以故事情节展示问题，关于图形表格或情节与图表结合的习题数加起来还不到总数的一半;相比之下北师大版问题表征的形式丰富且各形式分布均匀.

通过分析可得，人教版教材设置“一次函数”习题时，多以纯数字短语表现数学问题，直接聚焦到要考查的知识点，学生可以迅速调动已有的认知结构，快速迁移解决问题，但图形表格的表征方式运用少.北师大版教材中多以描述性语言和图形图象结合的形式出现，在设置较多纯数字短语和故事情节问题的基础上也很好地渗入图象表格，实现从纯知识点考查到情节图象结合的顺利过渡.

（3）任务特征

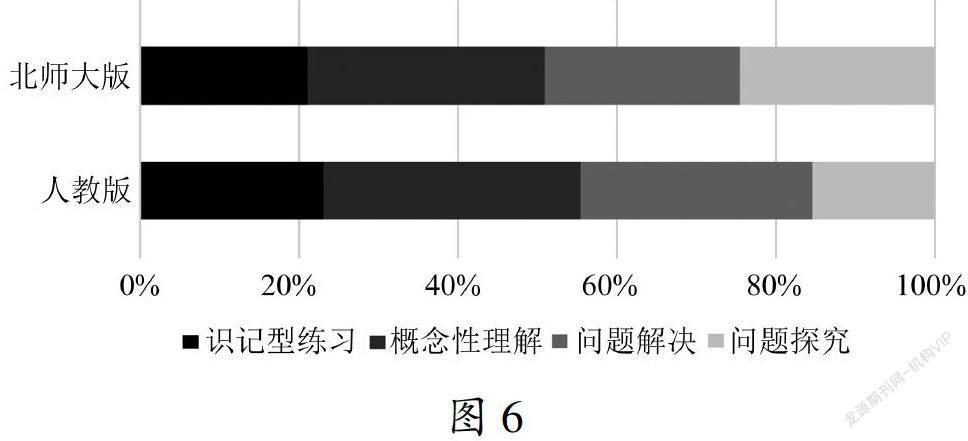
对两版本“一次函数”习题的任务特征水平进行比较，得到图6.两版本以“概念性理解”和“问题解决”为主，但北师大版涉及“问题探究”的比重远高于人教版.

由此可以看出人教版和北师大版“一次函数”内容在任务表征上有共同的突出重点，同时又各具特色.基于函数的抽象性，结合学生第一次接触函数的认知特点，两版本都以“概念性理解”为重点任务.人教版更注重基础性学习，对于“问题探究”方面的任务涉及比重较低;北师大版显然在任务难度高的水平之下合理设置了更多的数学问题.

4 进一步分析

在统计人教版和北师大版关于“一次函数”章节习题时，发现两版教材有涉及共同情境的习题，但表征方式和习题要求不同，为此，选取其中一些案例，作进一步的分析.

根据“小球滚动”设置数学问题情境，北师大版以文字描述的形式（表征特征S2）要求学生写出相应的解析式并判断函数类型（任务特征CU2）;而人教版以图文结合方式表征（PE4），要求学生写出解析式判断类型的同时并简单运用（任务特征PS3），人教版对此情境的刻画和运用更全面.此外，两版本都设置“电话计费”问题情境.以北师大版为例，如下：

北师大版“电话计费”问题情境

3.某电信公司手机的A类收费标准如下：不管通话时间多长，每部手机每月必须缴月租费12元，另外，通话费按0.2元/min计.

（1）写出每月应缴费用y（元）与通话时间x （min）之间的关系式;

（2）某手机用户这个月通话时间为180min，他应缴费多少元？

（3）如果该手机用户本月预缴了100元的话费，那么该用户本月可通话多长时间？

4.某电信公司手机的B类收费标准如下：没有月租费，但通话费按0.25元/min计.按照此类收费标准，分别完成第3题中的各小题.

※5.根据上面第3， 4题中的条件，完成下列各题：

（1）若每月平均通话时间为300 min， 你选择哪类收费方式？

（2）每月通话多长时间，按A， B两类收费标准缴费，所缴话费相等？

第3、4、5题属同一个问题情境（表征特征S2），但任务要求不同，难度也逐步增加.第3、4题主要考查学生对一次函数和正比例函数概念的理解与运用（PS3），5题是对知识点的综合运用（PE4）.这三道题巧妙地利用“电话计费”的情境，用不同梯度的问题，帮助学生完成单一的知识点到综合运用的过渡，而“电话计费”问题情境来源于生活，学生易理解，所以被两个版本教材所重视.类似地，如“某地气温变化”“追及相遇问题”“水池蓄水”等都秉持由简入深的原则，很好地将知识点与实际生活结合起来.

关于“一次函数”习题，两个版本都有各具特色的问题情境可供借鉴.如人教版中“活期储蓄”及“运输肥料”属于职业情境;北师大版利用“农作物产量”“植物生长”“温度换算问题”等很好地将数学与科学知识结合起来，学生可以体会到数学的科学价值与应用价值.此外，北师大版中还有一道题的情境为“小明绕赤道环行”，此情境与地理知识结合起来，要求学生阅读理解能力与综合运用能力，是很好的尝试.

5 启示

5.1 丰富情境类型，促进多元发展

数学是一门抽象的科学，数学情境的创设可以让数学知识具体化、形象化.习题情境类型的多样化，能促进发展学生数学学科核心素养，尤其是数学建模素养，创设不同类型问题情境，培养学生发现问题、提出问题、分析问题和解决问题的能力.设置多种类型的习题问题情境，既要注重知识与实际生活的联系，又应关注学科间的横向关联.学生在学会数学知识的同时也体会到数学与个人生活，未来发展，甚至社会发展之间的紧密联系.

5.2 图文表征问题，发展数形结合

表征数学问题的方式多种多样，要根据具体的数学内容来选择恰当的表征方式.“一次函数”处于初步培养学生数学抽象能力阶段，因此，更应贯彻具体与抽象相结合的原则，多用直观辩证的方式，帮助学生理解数学概念.“ 数缺形时少直观”，利用几何图形描述问题，借助几何直观理解抽象的算理，这是解决数学问题的有效手段之一.人教版侧重叙述性的文字描述，较少用直观的图象或表格来表征问题，因此，应增加图象或表格设置数学问题情境，在习题中培养学生数形结合的思想.北师大版较多地用到图象表征，可在此基础上加强图文间的相关性，充分发挥习题作用.

5.3 借鉴经典案例，学科相互交融

经典案例是知识点良好的载体，从不同角度设置问题，挖掘数学问题情境的价值.好的问题不仅可以快速引发学生的数学思考，调动学生已有知识体系，还能使学生认识到数学与外部世界的联系，由纵向思考拓展到横向学科间的思考.例如北师大版中以其他学科知识作为问题背景，创设问题情境，这会让学生体会到数学不是独立的一门学科，而是与其他学科相联系的.数学问题情境不仅应考虑个人发展，还应体现出数学与其他学科的联系.

参考文献

[1]吴立宝，洪梦，王富英.数学教科书例、习题的关系研究[J].中学数学教学参考，2021（08）.

[2]鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望，2002，31（09）：48-52.

[3]高文君，鲍建生.中美教材习题的数学认知水平比较——以二次方程及函数为例[J].數学教育学报，2009，18（04）：57-60.

[4]贾随军，吕世虎，李保臻.中国与美国初中数学教材习题的个案比较——以“与三角形有关的角”为例[J].数学通报，2014，53（09）：17-23.

[5]吕传汉，汪秉彝.论中小学“数学情境与提出问题”的数学学习[J].数学教育学报，2001（04）：9-14.

[6]常磊，鲍建生.情境视角下的数学核心素养[J].数学教育学报，2017，26（02）：24-28.

[7]陈志辉.中美两国初中数学课程的问题情境水平比较研究——以“函数”内容为例[J].数学教育学报，2016，25（01）：5-9.

作者简介 张丹亭（1999—），女，甘肃天水人，硕士研究生，研究方向：数学教学论.