二维梯形沉积盆地放大效应的数值模拟研究

包得志,荣棉水,喻 烟

(1.应急管理部国家自然灾害防治研究院,北京 100085;2.北京工业大学,北京 100124)

0 引言

“盆地效应”是指入射到盆地内部的地震波由于基岩和土层介质阻抗比的差异,能量被捕获于盆地内沉积物中且难以向盆地外释放,从而显著地改变地震动的频率、振幅和持续时间并给盆地内部建筑物造成严重的破坏。

1985年墨西哥大地震,距震中400 km外位于盆地中的墨西哥城震害十分严重,经研究人员事后调查指出城市震害异常与该城市坐落于沉积盆地有关[1-2]。1995年日本神户地震后在大阪盆地边缘形成了一个长约20 km、宽约1 km的条带状严重破坏区,事后Hiroshi Kawase[3]通过数值模拟的方法研究发现,由于介质阻抗比的差异盆地边缘处诱发了面波并和直达体波发生相干干涉使震动增强,并首先将这一现象定义为盆地的边缘效应。Bard和Bouchon[4]研究了P波和SV波入射两个基岩和土层波速差异不同的二维盆地对比发现,波速差异较大的宽盆地激发的瑞利面波的振幅比要比波速差异较小的盆地大。Khanbabazadeh等[5]分析了不同土质类型和不同强度的入射波对二维盆地放大的影响,结果表明,不同土质类型的盆地在不同激励水平下的放大行为存在较大差异。另外Khanbabazadeh等[6]从微震调查和岩土工程调查获得的数据建立了土耳其杜兹切盆地边缘模型,发现倾斜的基岩对盆地边缘特性影响很大。Zhu等[7]建立了二维浅层盆地的数值模型,并将其响应与工程上常用的一维响应分析做比较,来分析侧向非均质性引起的附加放大效应。陈国兴等[8]利用收集到的钻孔及其他地质资料建立了福州盆地的仿真模型并用地震波垂直入射,发现在盆地边缘处产生明显的边缘效应,在几何形状突变处聚焦效应明显。刘中宪等[9]利用间接边界元法研究了半空间椭球形沉积盆地对地震动响应,结论是盆地形状对地震动放大效应和空间分布特征具有明显的影响。李雪强[10]采用显式有限元法研究了盆地基岩倾角和覆盖层厚度对盆地内面波发育及盆地边缘效应和聚焦效应的影响。王建龙[11]利用显式有限元法研究了盆地放大效应与盆地深度的关系。于彦彦[12]利用谱元法研究了四川盆地的地震动响应,并认为四川盆地基底深度的分布对盆地内强地震动分布有较大影响。张建经等[13]选用三个卓越频率不同的Ricker子波作为输入,研究了不同卓越频率的输入波对盆地地震反应的影响。

通过以上学者们的研究,可以得知盆地的几何形状、介质的材料性质以及入射波的频率成分对盆地的放大效应都有较大的影响。但是以上学者的研究并没有对盆地效应的影响因素做统一的无量纲处理,得出的研究结论只适用于特定的研究模型,本文采用Buckingham[14]提出的π定理,将盆地的几何形状、材料性质和入射波频率等影响因素做无量纲处理。并利用显式有限元方法和透射人工边界[15]建立了二维梯形盆地的粘弹性数值分析模型,以SH波垂直入射来研究盆地几何形状、介质物理参数以及入射波频率对地震动放大的影响。

1 计算方法和输入波

1.1 计算方法

本文采用的数值计算方法是显式有限元法结合透射人工边界,模型的介质为黏弹性介质,计算区内网格节点的运动动力方程:

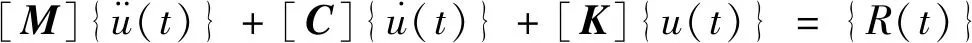
(1)

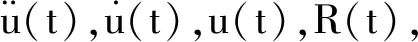
[C]=α[M]+β[K]

(2)

式中:α、β为比例系数,其取值决定体系阻尼效应的大小。在瑞利阻尼模型下阻尼比ξ和入射波频率满足以下关系,其中f为入射波的频率:

ξ=0.5(α/f+βf)

(3)

在本文当中α、β分别取0.025和0.02,入射SH波的主频f0为1.1 Hz,模型最大阻尼比约为0.022 4。

单元刚度矩阵为:

(4)

单元等效节点荷载向量:

(5)

式中:[N]为单元形函数矩阵,[B]为单元几何矩阵;t为单元厚度,它为一常数;[D]为材料矩阵,并且有如下关系:

对于SH问题有

(6)

透射人工边界的设置保证波在人工边界处的传播特性与在原连续介质中一致,使得波通过人工边界时无反射效应发生完全透射,从而实现对原连续介质的精确模拟。透射边界利用内点位移表示边界点位移,随着引入内点数量的增加,可以建立高精度的高阶透射公式。透射边界将边界波场分为内行波场和外行波场,运用透射边界在边界节点建立运动方程时必须分离出外行波,设分离出的外行波场位移为u外行,全波场位移为u总,内行波场为u内行,三者满足如下关系:

u外行=u总-u内行

(7)

在图1中,设x轴的原点O设置在所考虑的人工边界点上,垂直于人工边界并指向外部无限域,则可将外行单向波位移场表示成一系列外行平面波位移场的叠加,即:

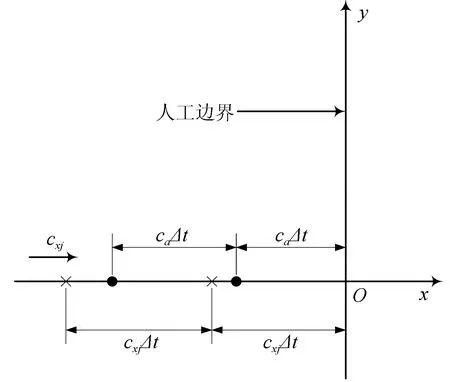
图1 透射人工边界示意图Fig.1 Diagram of transmission artificial boundary

(8)

由于不同的外行波分量视速度不同,为了解决这一问题引入了一个共同的常值人工波速ca来近似替换不同的视波速cxj式(8)则变为:

(9)

N阶多次透射人工边界(MTF)格式如下:

(10)

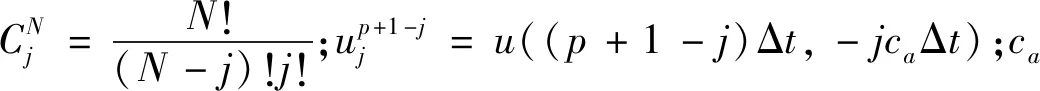
u(pΔt+Δt,0)=2u(pΔt,-caΔt)-

u(pΔt-Δt,-2caΔt)

(11)

1.2 输入波

本文选择雷克子波作为场地反应的输入波(图2),并以SH波垂直入射盆地模型,雷克子波波形简单,只有一个正峰,两侧各有一个旁瓣,收敛快延续时间短,雷克子波的表达式为:

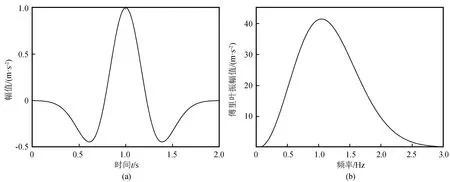
图2 入射波时程及傅里叶振幅谱Fig.2 Incident wave time history and Fourier amplitude spectrum

R(t)=[1-2(πf0t)2]exp[-(πf0t)2]

(12)

其中f0为输入的雷克子波主频。

2 计算模型及参数无量纲处理

2.1 计算模型

如图3所示,研究的梯形盆地的深度为h,盆地的开口宽度为2d+L,土层介质的剪切波速、密度和泊松比为vS1、ρ1和υ1。基岩介质的剪切波速、密度和泊松比为vS2、ρ2和υ2。

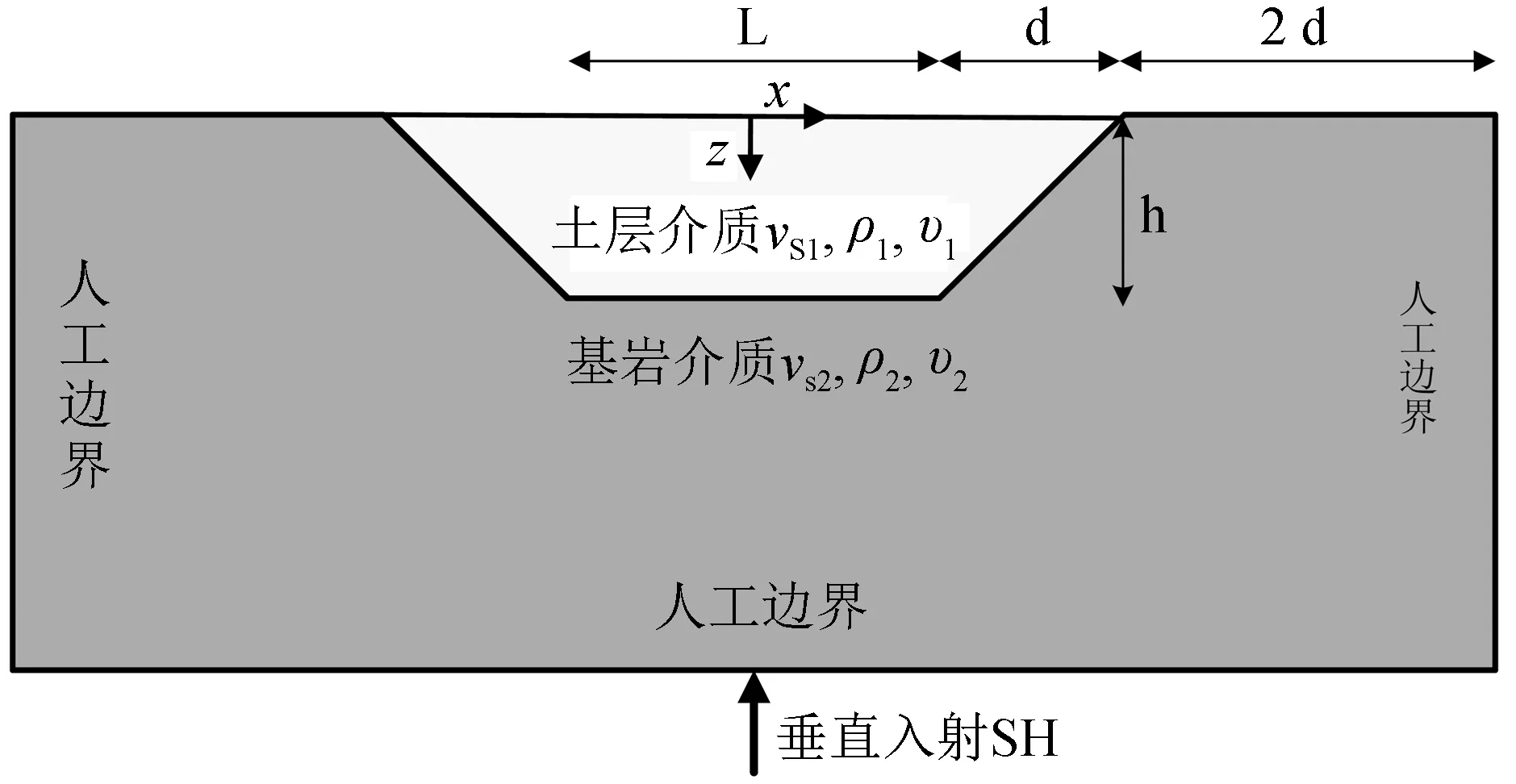
图3 二维梯形盆地模型示意图Fig.3 Schematic diagram of two-dimensional trapezoidal basin model

影响盆地放大效应的物理参数包括:盆地的几何形状、材料性质、入射波的频率。所研究的梯形盆地模型为一种理想化盆地模型。它的各项几何指标很容易被参数化。通过将所研究盆地的各项物理参数进行无量纲处理后所得到的结果更具有普适意义。在所研究的梯形盆地模型当中,土层和基岩的分界面可由下面的数学表达式表示:

(13)

在本文当中梯形盆地的所有计算模型都是基于宽度L=2d来计算的,放大系数β定义为盆地地表加速度峰值与入射波加速度峰值的比值[16]。

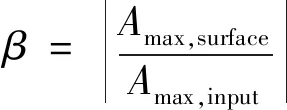
(14)

2.2 影响参数无量纲化处理

对于动力学问题可以用三个参数来表示材料的属性,分别是剪切波速vS、介质密度ρ以及泊松比υ[17]。vS1、ρ1和υ1分别表示土层介质的剪切波速、密度和泊松比。vS2、ρ2和υ2分别表示基岩介质的剪切波速、密度和泊松比。根据量纲分析原理中的π理论[18],任何一个由n个有量纲的物理量参与的物理过程中的函数关系都可以转换成由n-k个这些物理量组成的无量纲量πi之间的函数关系,其中k是具有独立量纲的物理量的数。由于这些无量纲量是以不同的πi来表示的,故称为π定理。根据这条定理,通过物理关系式将研究参数转化为无量纲形式,减少研究函数中自变量的个数,从而有利于实验处理和分析。结合模型的几何参数以及材料性质参数本文定义以下几个无量纲参数:

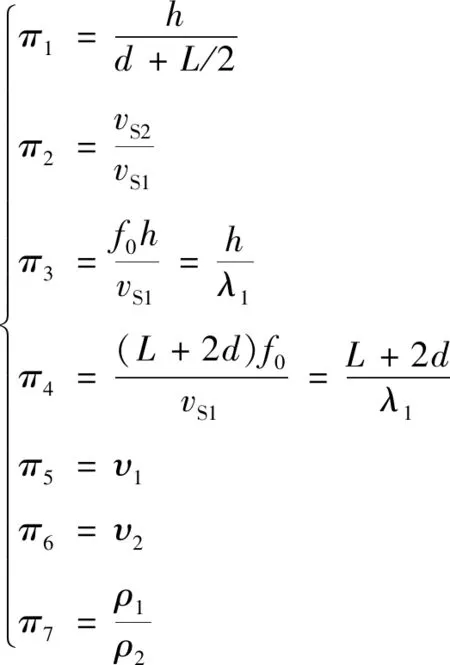
(15)

式中:π1为模型深宽比;π2为模型的横波波速比;π3为无量纲频率;π4为无量纲盆地宽度;π5为土层介质泊松比;π6为基岩介质泊松比;π7为介质密度比;λ1为输入地震动在土层介质中的主频波长;λ2为输入地震动在基岩介质中的主频波长;f0为入射波的主频。

由于π5、π6和π7对盆地效应的影响不大,且以SH波作为输入波泊松比基本上无影响,为了减少计算量在所有的计算模型中这三个影响因素都设为定值π5=0.3,π6=0.3,π7=0.98。接下来本文将研究盆地深宽比π1、模型波速比π2、盆地深度和入射波长比π3以及盆地开口宽度和入射波长之比π4这四个影响因素对盆地放大效应的影响。

3 计算结果及分析

3.1 深宽比π1对放大系数的影响

深宽比π1为梯形盆地尺度的纵横比,并且盆地的深宽比是支配盆地地震反应的一个重要因素[19]。在本小节,结果都是在盆地深度和入射主频波长之比为1(即π3=1),图4给出了盆地深宽比π1分别取值为0.5、0.25、0.17、0.13时,地震动放大系数β在地表的分布。

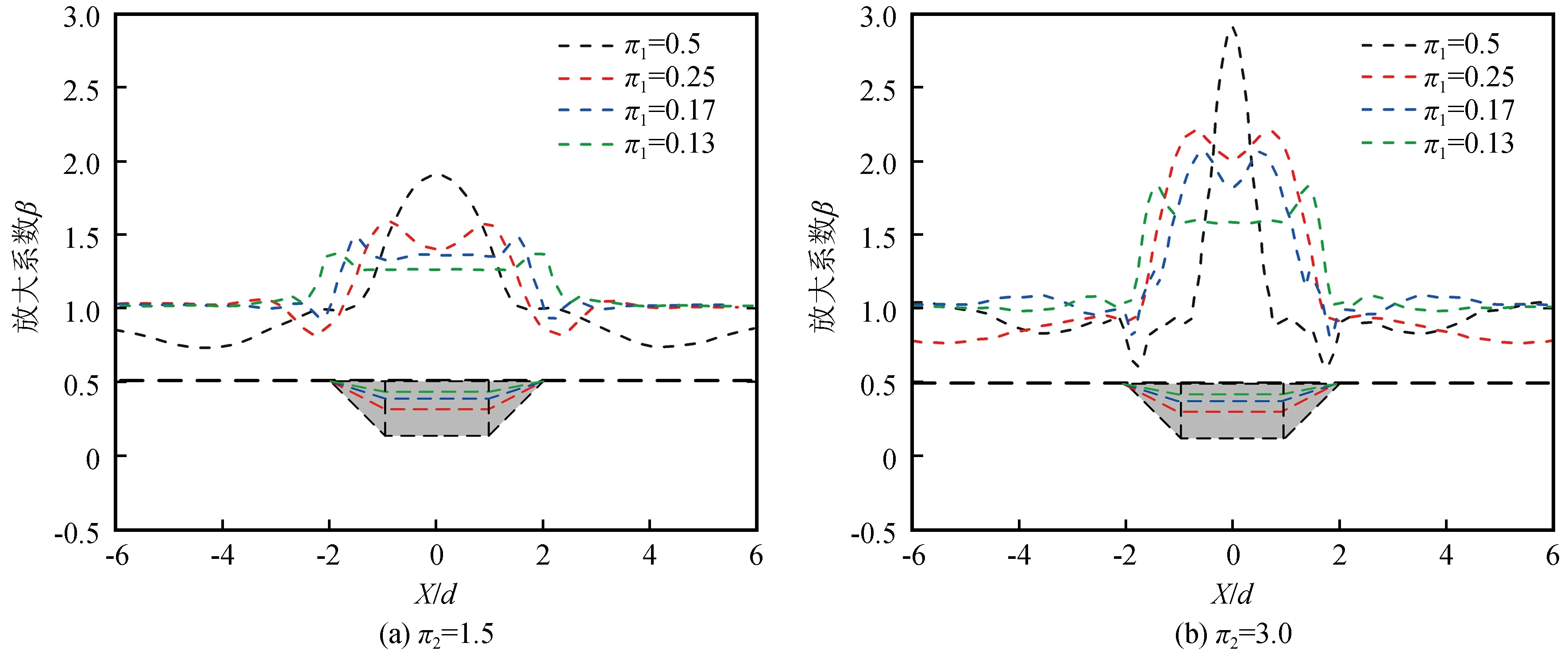
图4 深宽比π1对放大系数的影响Fig.4 Effect of depth-width ratio π1 on amplification factor

从图4(a)、(b)两图中可以看出,无论在波速比π2为1.5或3时,盆地深宽比π1对放大系数β的影响都十分显著,且变化趋势基本一致,随着深宽比值逐渐减小,盆地表面各处的放大系数β都有逐渐减小的趋势,π1值越大盆地边缘越陡峭盆地较深,盆地的聚焦效应越明显[20],如π1=0.5时,此时盆地边缘最陡峭,图4(a)、(b)两图的放大系数最大值都出现在盆地中心位置,波速比π2=1.5时最大值为1.85,当π2=3时最大值为2.9。在π1=0.5时,图4(a)、(b)两图放大系数分布都为单峰,在π1分别取0.25、0.17、0.13时,即对于较浅的盆地,放大系数β的最大值出现在盆地边缘附近,这是因为盆地边缘处诱发的面波与入射体波发生相长干涉,诱发的边缘效应[21],放大系数整体上呈双峰分布。纵向比较图4(a)、(b)两图可以发现,盆地基岩和土层的波速比π2对放大系数的影响也十分巨大,在深宽比相同的情况下,π2=3时的放大系数要整体上大于π2=1.5时的放大系数。

总之π1越大盆地越深,诱发的盆地聚焦效应越明显,π1值越小盆地越浅,诱发的盆地边缘效应就越显著。并且随着π1值逐渐减小,在波速比不变的情况下,放大系数β有逐渐减小的趋势。且在盆地深宽比相同时,基岩介质与土层介质波速比越大,放大系数越大。

3.2 波速比π2对放大系数的影响

选取盆地内部中心位置处的观测点为研究对象,如图5所示。给出了放大系数β与波速比π2之间的关系,在盆地深度和入射波长之比π3和盆地深宽比π1相同的情况下,改变波速比π2的值,将π2值分别取为(1.5、2.0、3.5、5.0),介质的波速比不断增大,从图5的(a)、(b)、(c)、(d)都可以看出随着波速比π2增大,放大系数也逐渐增加。这主要是由于随着波速比增大,土层和基岩介质的阻抗比就越大[22],土层沉积物所捕获的入射地震动的能量百分比就越高,能量透射到基岩的比例就越小,导致放大系数越大[23]。

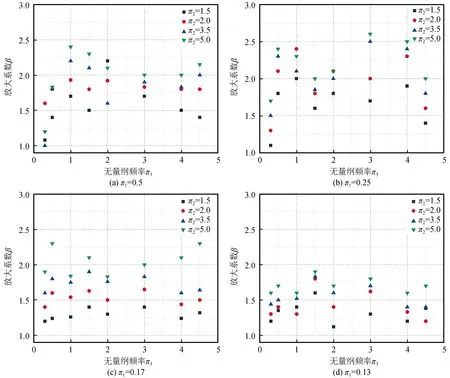
图5 波速比π2对放大系数的影响Fig.5 Effect of wave velocity ratio π2 on amplification factor

3.3 无量纲频率π3对放大系数的影响

在本小节中,定义了有关输入地震动主频的一个参数π3。π3通过量化盆地深度与入射主波长的相对大小来测量盆地对入射波频率的响应。

(16)

由于前面的结果发现π1=0.5时放大系数β最大,因此本小节中所有结果都是基于深宽比π1=0.5时得到的。图6给出在不同波速比π2的情况下,π3不断变化时对放大系数β的影响。改变入射波主频f0来改变入射波的波长λ1,进而改变π3值。π3分别取值0.5、1、4。因为在π3小于0.5或是大于4的情况下,盆地深度相对于入射波长来讲都太小或者太大。π3取0.5时入射波主频波长相当于盆地深度的2倍,π3取1和4时,入射波主频波长相当于盆地深度的1倍和0.25倍。从图6(a)、(b)可以看到,π3=4时,盆地深度相对于入射波主频波长较大时,放大系数分布出现两个峰值,峰值出现在X/d=±1左右。π3分别等于0.5或1时,盆地深度相对入射主频波长较小时,放大系数分布呈单峰分布,放大系数峰值出现在盆地中心位置。在图6(c)中,当波速比较大时,即π2=3.5时,放大系数全都为单峰分布,峰值出现在盆地中心,并且π3=4盆地中心处放大系数最大,π3=1时次之,π3=0.5时盆地中心放大系数最小。纵向比较图6(a)、(b)、(c)三个图可以发现,对放大系数影响最大还是波速比π2,随着基岩和土层介质的波速比增大,放大系数β明显增大,最大放大系数出现在图6(c)π2=3.5时的盆地中心位置,大约为3.2倍左右。

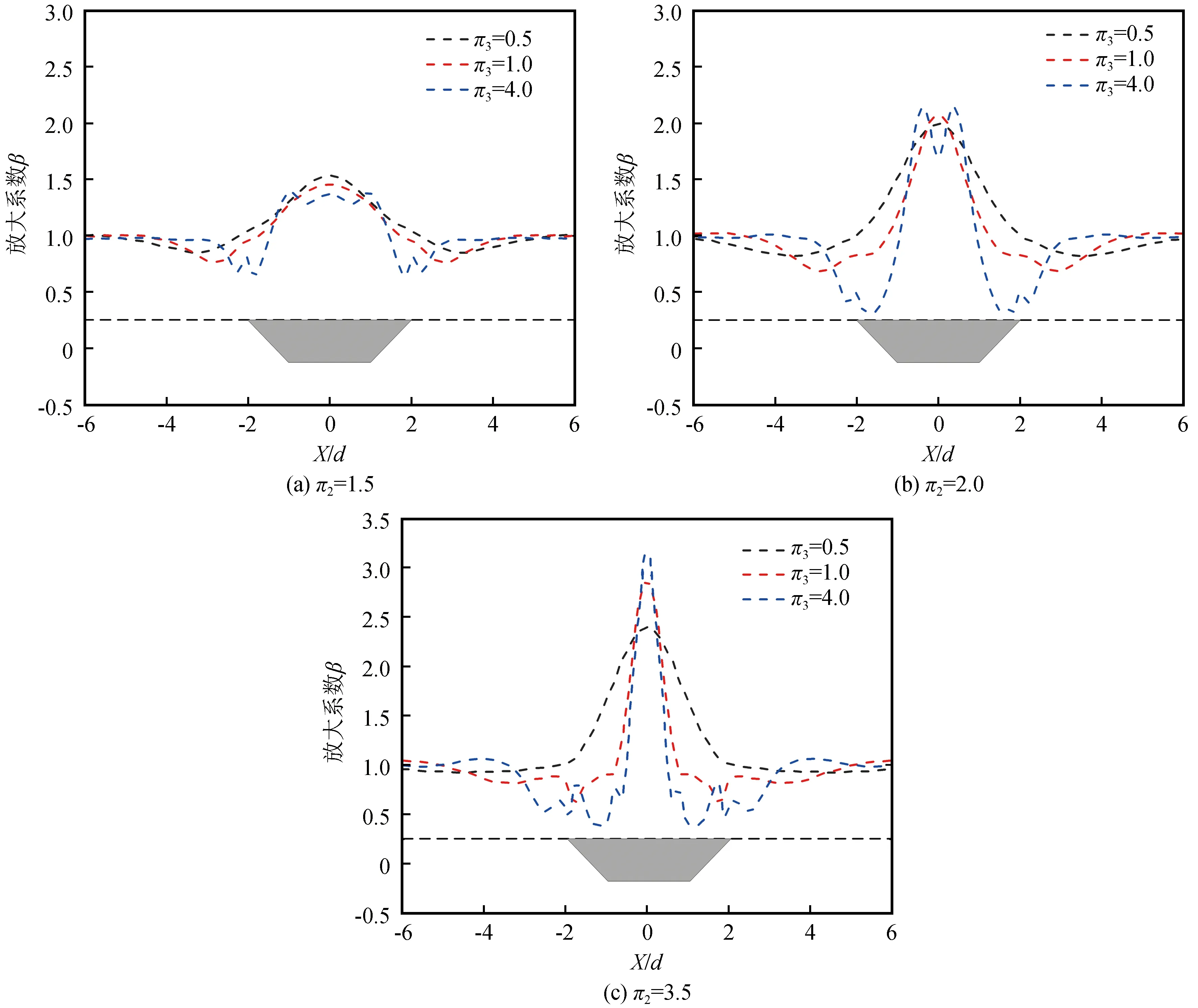
图6 无量纲频率π3对放大系数的影响Fig.6 Influence of dimensionless frequency π3 on amplification coefficient

3.4 无量纲化盆地宽度π4对放大系数的影响

最后研究盆地无量纲宽度π4对地震动放大系数β空间分布的影响。

(17)

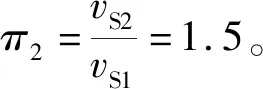
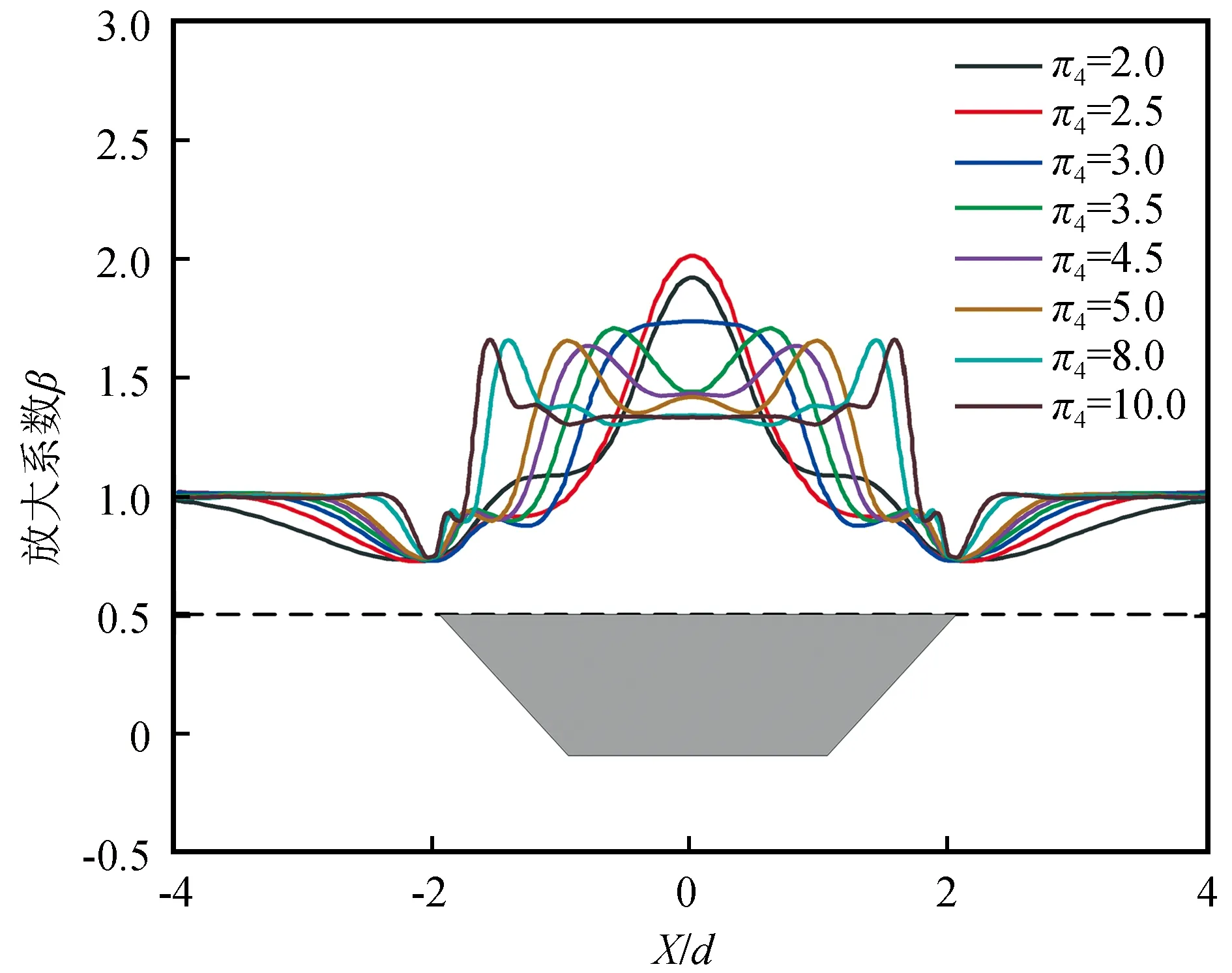
图7 无量纲宽度π4对放大系数的影响Fig.7 Influence of dimensionless width π4 on amplification factor

4 总结

本文将二维梯形盆地对地震动影响的主要物理参数分为三类:盆地的几何参数(包括盆地的深宽比、盆地的开口宽度)、盆地的材料物理参数(包括基岩和土层的剪切波速、泊松比和介质密度)以及入射波物理参数(入射波的主频频率以及主频波长)。根据Buckingham的π定理定义了影响盆地放大的7个无量纲参数。并分别研究了盆地深宽比π1、介质波速比π2、盆地深度与入射波主频波长之比π3、以及盆地开口宽度与入射波主频波长之比π4、对地震动加速度峰值放大系数β的影响,通过研究发现:

(1)在入射波波长和介质波速比确定的情况下,π1越大盆地越深,诱发的盆地聚焦效应越明显,π1值越小盆地越浅,诱发的盆地边缘效应就越显著。

(2)在盆地的深宽比一定时,随着π4值的不断增大盆地的峰值放大系数逐渐从盆地中心移向盆地边缘,表现出越来越明显的边缘放大效应。

(3)对峰值放大系数影响最明显的是介质的波速比π2,波速差异越大,放大系数β从整体上要比介质波速差异情况较小时大,并且π2越大,使得入射波在基岩土层分界面处折射角变大,盆地更倾向于在盆地中心处出现最值放大系数。