基于概率密度演化的基础隔震结构随机响应分析
2021-12-08叶东繁刘彦辉周福霖
叶东繁,刘彦辉,秦 熙,谭 平,周福霖
(1.广州大学工程抗震研究中心,广东 广州 510405;2.广州大学减震控制与结构安全国家重点实验室培育基地,广东 广州 510405)
0 引言
伴随着社会科技的进步,减隔震技术也得到了大力的发展。目前基础隔震技术因其具有力学模型简单、机理清晰、减震效果明显等优点已经在工程结构中被广泛应用。在当前抗震设计规范中,结构在进行地震时程分析时,往往是进行确定性动力分析,但是在实际工程中,地震激励具有明显的随机性,因此有必要对基础隔震结构进行随机振动分析并给出全面的概率信息,也为随机结构动力可靠性的精细化分析提供更多依据。
经过几十年的发展,线性系统的随机振动分析取得了成熟的理论成果。以朱位秋为首的几位学者发展了哈密顿理论体系框架,结合随机平均法,获得了多自由度体系FPK方程的稳态解,但也仅限于较低的维数[1]。芮珍梅等[2]通过引入等价漂移系数,将联合概率密度函数满足的高维FPK方程转化为一维FPK型方程,建议了构造等价漂移系数的条件均值函数方法,采用路径积分方法求解降维FPK型方程。林家浩[3]建立和发展的虚拟激励法通过将平稳随机振动分析转化为简谐振动分析,将非平稳随机振动分析转化为确定性时间历程分析使其计算步骤大大简化,但仍然可以保持理论上的精确性。李创第等[4]采用复模态法进行解耦,通过以多振型表示的结构地震响应的计算表达式,计算分析了基础结构在随机地震作用下的响应。作者课题组[5-6]采用虚拟激励法对框架-剪力墙层间隔震结构分别进行了小震和大震下的随机响应分析。但这些方法通常只能得到结构响应的二阶统计矩,很难全面地反映结构在随机激励下的力学性能。
近年来兴起的概率密度演化方法为一般结构的随机振动及可靠度分析[7-8]提供了一条新的道路。该方法基于物理和力学规律导致的系统物理状态演化现象,对概率守恒原理进行了分析,发现了概率密度演化与物理系统状态演化的内在联系,从而导出新的概率密度演化方程,可以直接得到结构随机响应的概率密度函数及其演化分布,具有广泛的适用性,适用于随机结构的线性与非线性分析。孙臻等[9]通过改变基础隔震结构的设计参数,在考虑激励随机性的基础上,研究了基础隔震结构非线性随机地震响应的概率密度演化规律,发现通过改变结构的阻尼比、周期比和屈重比的取值可以控制结构上部和下部的位移。
本文基于概率密度演化理论对抗震结构和基础隔震结构进行随机地震作用下的响应分析并进行对比,研究基础隔震结构在随机地震作用下的减震效果。通过引入工程地震动物理随机函数模型,采用数论选点法对多维外荷载随机变量选取离散代表点,并求得相应赋得概率,利用离散代表点合成地震动加速度时程样本作为随机激励,输入结构。在求得结构响应及其相关导数后,应用TVD差分格式求解广义概率密度演化方程即可得响应的时变概率密度及其演化。结果表明:在随机地震作用下,基础隔震结构相较抗震结构具有良好的减震性能,隔震层的设置能够减小结构位移响应的标准差,减少了结构响应的离散型;概率密度演化方法不仅能够给出结构响应的二阶统计矩,还能全面地反映结构响应的时变概率信息,位移响应的概率密度函数分布不服从正态分布或其他常用分布,且随着时间演化。
1 概率密度演化理论及数值求解
1.1 概率守恒原理
概率守恒原理是概率密度演化方法的理论基础。从一般意义上说,概率守恒原理可以表示为:如果随机因素在随机系统中是保守的,即没有新的随机因素加入,也没有已有的随机因素消失,那么该保守系统在状态演化过程中概率守恒。一般从状态空间描述和随机事件描述这两个方面来研究这一原理。
随机事件描述即为:给定分布空间中的任意随机事件{Y0∈Ω0}在保守系统的状态演化过程中演化为{Y(t)∈Ωt},其概率不变,即Pr{Y0∈Ω0}=Pr{Yt∈Ωt}。随机事件可以是基本随机事件的复合。状态空间描述为:给定一个在分布空间Y内任意时刻t的瞬时速度场v(y,t),该速度场的任意区域Dfixed在经过任意时间区间[t1,t2]内,穿越该区域边界进入和离开的概率之和等于该区域内概率的增量。只有在整体的保守状态空间中,其任意区域的概率流动满足守恒原理。状态变量之间是相互耦合地,若仅仅只考虑某个子空间时,很难完全考虑到子空间中的全部概率产生源,不能保证子空间的概率是守恒的。随机事件的描述恰能解决这一难题。随机事件可以是任何子事件的复合,故可以对随机事件进行分解。
1.2 广义概率密度演化方程
一般多自由度结构体系的运动方程可表示成:
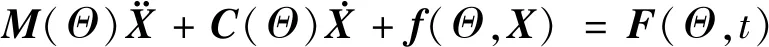
(1)
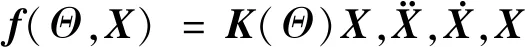
通常在工程实际中,结构动力学问题都是适定的,即所求的结构响应解答都是唯一存在的,且跟结构参数和激励的随机性有着很大的关系。当所求结构响应为位移时,其物理解答可表示为:
X(t)=G(Θ,t)
(2)
类似的,其速度也可以表示成:

(3)
且存在H(Θ,t)=∂G(Θ,t)/∂t。
假设θ为随机参数向量空间中确定代表点,从概率事件描述的角度进行推导可得到广义概率密度演化方程,
(4)
在给定结构的边界条件和初始条件下求解广义概率密度演化方程,并根据下式求X(t)的概率密度函数:
(5)
一般情况下,方程(4)的边界条件可采用:
pXΘ(x,θ,t)|zj→±∞→0,j=1,2,…,m
(6)
初始条件为:
pXΘ(x,θ,t)|t=t0=δ(x-x0)pΘ(θ)
(7)
1.3 数值求解
广义概率密度演化方程的求解需要联合式(1)和式(3),并结合其边界条件和初始条件。本文在只考虑地震动随机性的基础上,基于“震源-传播途径-局部场地”的物理机制,根据工程地震动物理随机函数模型[10],将地震动物理随机函数模型中的圆频率ω进行离散,假定每一个离散的频率窄区间对应一个窄带谐波叠加分量,将各个频率分量对应的窄带谐波叠加分量相累加即可得到地震动时程样本。即:
(8)
其中:
(9)
(10)
(11)
(12)
式中;aR(t)为地震动加速度时程样本;t为时间;ω为圆频率。在该物理随机函数模型中,R为震中距;k为传播衰减系数,通常取经验值为1×10-5s/km。a、b、c、d均为地震波传播波数-频率关系函数中的经验系数,分别取为a=1.02,b=403 rad/s,c=1.89 s/rad,d=0.13 rad/m。取A0、T、ωg、ξg为4个相互独立的随机变量。A0为震源幅值参数,表示震源幅值强度;T为Brune震源参数,表示震源属性;ωg为场地等效卓越圆频率;ξg为场地等效阻尼比。假定4个物理随机变量均服从对数正态分布,其概率分布函数参数列于表1。
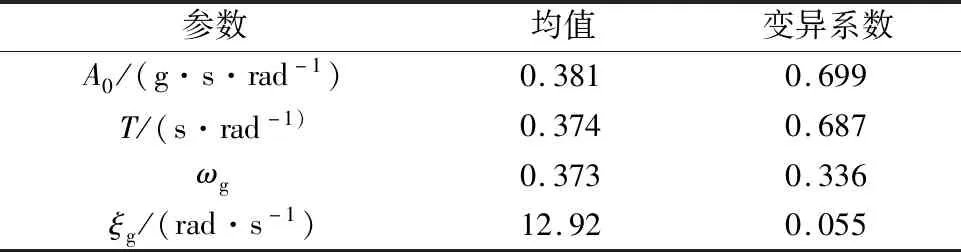
表1 物理随机变量的均值与变异系数Table 1 Mean value and coefficient of variation of physical random variables
选定随机变量后,本文采用数论选点法[11]进行随机变量离散代表点的选取。对于s维随机变量空间,选择一组生成矢量(n,h1,h2,…,hs),由生成矢量通过式(13)获得单位超立方体Cs[0,1]s内的散布点列。
qk,j=khj(modn)
xk,j=(2qk,j-1)/2n;k=1,2,…,n;j=1,2,…,s
(13)
其中
xk,j∈[0,1]
(14)
通常,对于大多数类型的概率分布呈现球对称或近球对称,特别是对于正态概率分布具有球对称性质,在其他类型的分布场合,其概率密度函数往往也呈辐射状衰减,虽然可能不是完全球对称的。因此,在超立方体内边缘角落部分的点可以忽略,仅考虑超球体内的代表点。对单位超立方体内的点进行筛选:
(15)
对经s维超球体筛选后的点集进行仿射变换,得到概率分布空间ΩΘ中的均匀点集:
(16)
式中:uj,δj为第j个随机变量的均值和变异系数;λ为随机变量的截取界限值。
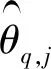
(17)
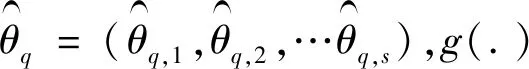
代表点θq,j的初始赋得概率为
(18)
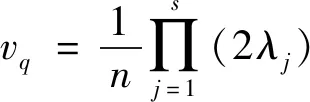
pΘ(θq,1,θq,2,…,θq,s)=p(θq,1)·
p(θq,2)·…·p(θq,s)
(19)
将所有点的概率进行归一化处理,可得:
(20)
根据生成的离散代表点由式(8)合成地震波作为输入结构的随机激励样本。对于每条地震波,相当于一个确定性动力反应分析过程,采用Newmark-β时程积分方法。计算可得到结构每层位移、速度和加速度。
求得结构的响应及其时间导数后,即可求解广义概率密度演化方程从而得到响应的概率密度函数。
本文采用TVD差分格式[13]对广义概率密度演化方程进行求解。其中步长的大小影响分析的精度和稳定性,TVD差分格式中的精度和稳定性要求的步长小于确定性分析,所以文中对确定性分析提供的速度时程进行线性插值以构成TVD差分格式中偏微分方程中的时变系数,获得满足符合精度条件的散点个数,从而保证TVD差分格式中的精度和稳定性。
TVD格式是在Lax-Wendroff格式的基础上施加通量限制器构成的,格式如下:
(21)
其中网格比λ=Δt/Δx,a为所求物理量的导数。φ为通量限制器,且0≤φ≤1,当φ=0时,式(21)退化为单边差分格式,当φ=1时,则为双边差分格式。
选择较小耗散的Roe-Sweby通量限制器,如下:
φsb(γ+)=max(0,min(2γ+,1),min(γ+,2))
φsb(γ-)=max(0,min(2γ-,1),min(γ-,2))
(22)
进一步考虑差分方向的自适应功能,即:
(23)
u(·)为单位阶跃函数。
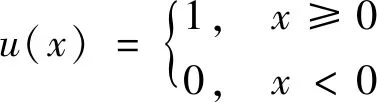
(24)
其中:
(25)
(26)
为保证TVD格式的稳定性和收敛性,需满足CFL条件,即|λa|≤1。
求得pXΘ(x,θ,t)后根据式(5)即可得到所求响应的概率密度函数。
2 结构模型
分别建立抗震框架结构模型和基础隔震结构模型,为了准确对比分析,隔震体系的上部结构与抗震结构相同,其模型如图1所示。上部结构层高3.6 m,隔震层高1.6 m。立柱截面尺寸为600 mm×600 mm,主梁截面尺寸为500 mm×300 mm,次梁截面为400 mm×300 mm,隔震层梁截面为500 mm×300 mm,板厚120 mm。混凝土强度等级为C30,场地类别为Ⅱ类。根据生成的离散代表点由式(8)合成284条地震波作为输入结构的随机激励样本。对抗震结构和基础隔震结构在Ⅶ度(0.15g)多遇地震下进行弹性分析。
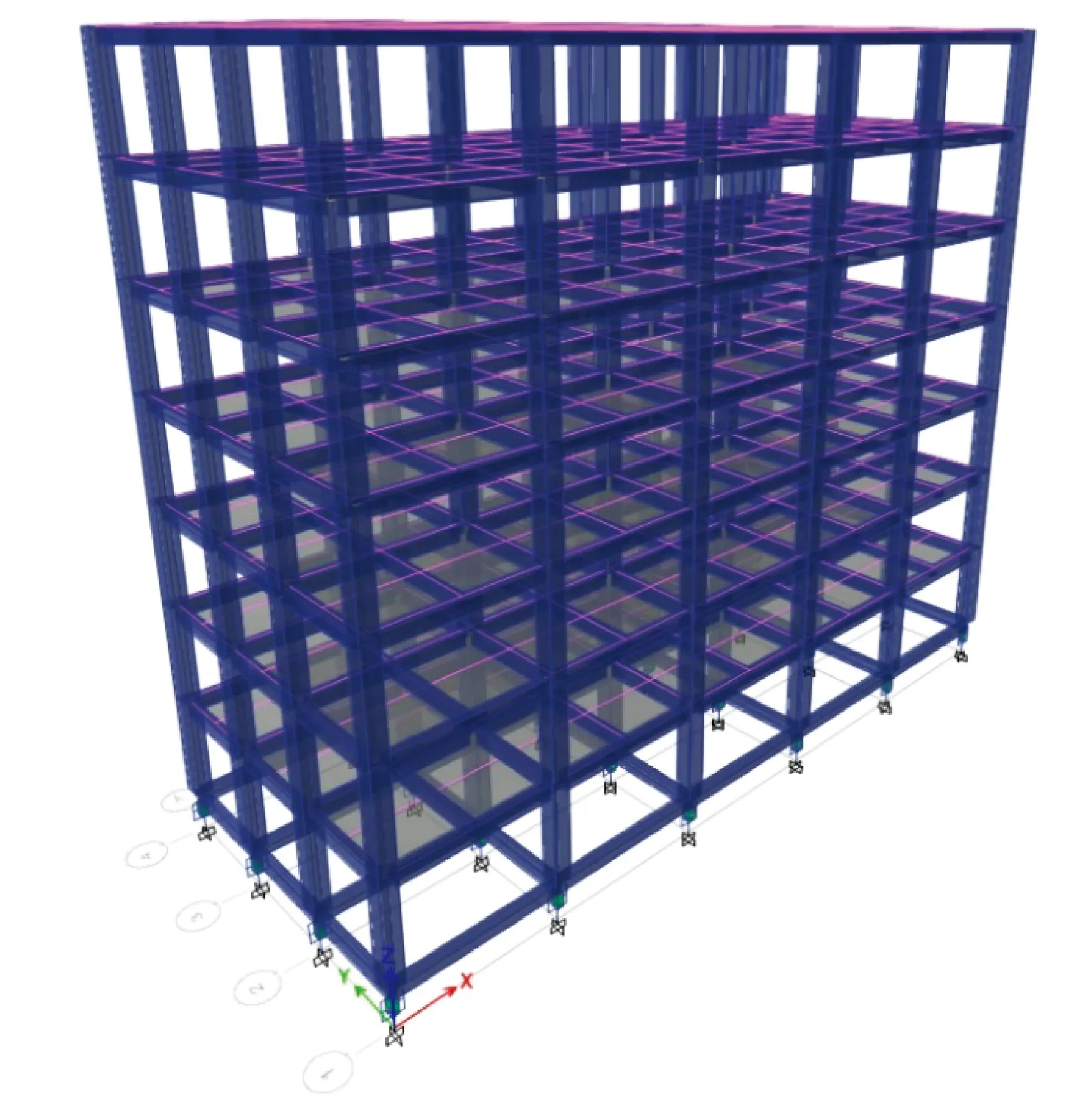
图1 基础隔震结构模型Fig.1 Model of base isolation structure
根据隔震层上部结构的柱底反力和结构的受力特点选用LRB500和LNR600两种橡胶隔震支座,布置采用一柱一支座的形式,其布置如图2所示。
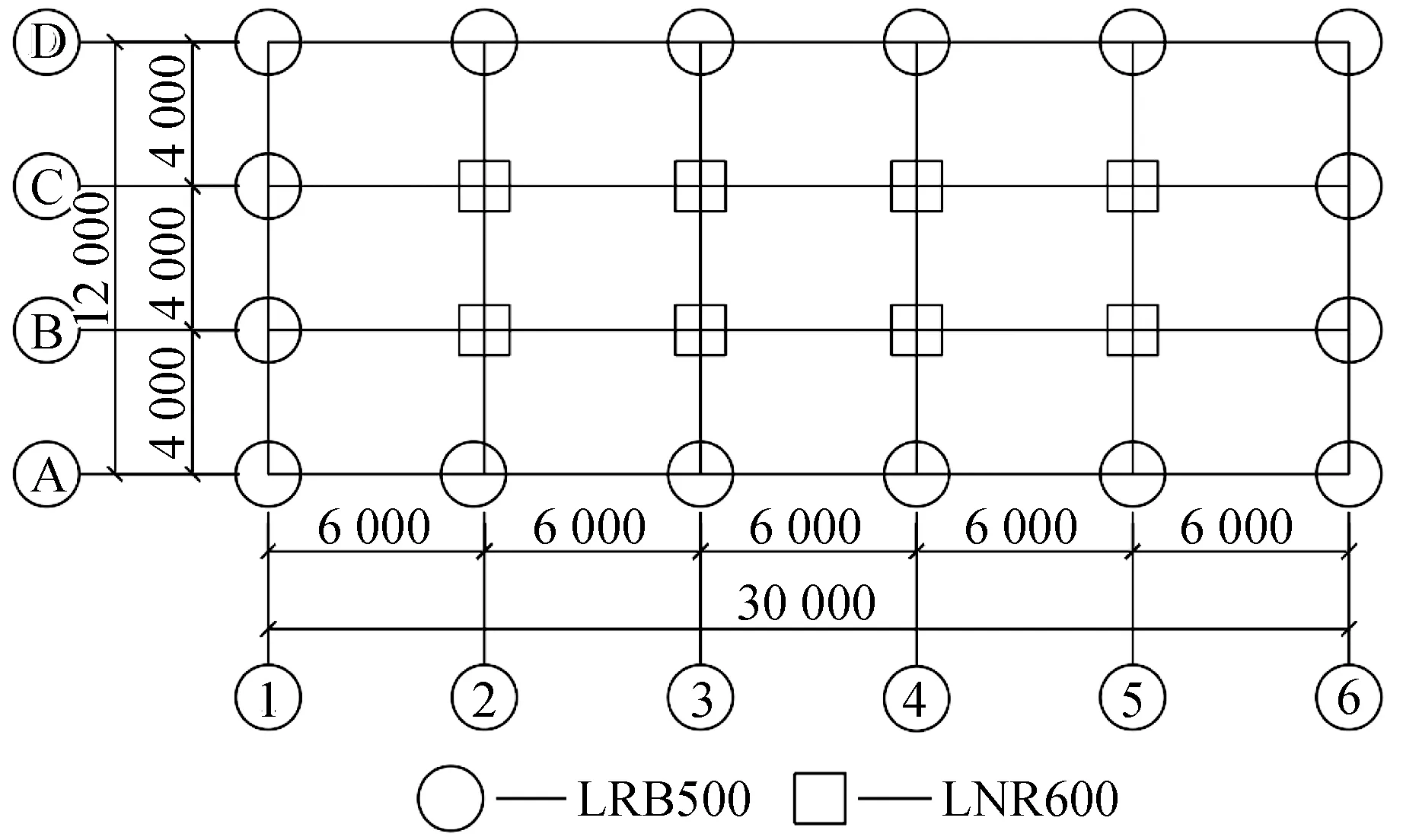
图2 隔震支座布置示意图(单位:mm)Fig.2 Schematic diagram of isolation bearing arrangement (Unit:mm)
建立与Etabs模型等效的Matlab仿真模型结构。
Matlab仿真模型采用糖葫芦串模型,将每一楼层看成一个质点,每层的质量集中在各楼层楼面处,然后用一根竖杆将每一个基本单元串联起来,即层剪切模型。为简化问题,一般做出如下假定:
(1)楼板面内刚度无穷大,不考虑其平面外的刚度;
(2)不计竖向杆件的轴向变形。
3 基础隔震结构随机响应对比分析
通过MATLAB程序对两种结构进行随机动力响应计算并统计分析。首先,需要将结构简化成集中质量质点系模型,输入地震波时程样本进行动力计算。其中简化的质点系模型的结构阻尼矩阵需要通过计算得出,本文考虑采用Rayleigh阻尼。首先从Etabs中导出结构的质量,和采用柔度法导出结构的刚度。然后通过获得的质量和刚度,采用Rayleigh阻尼法分别对结构的隔震层和上部结构的阻尼进行计算,然后进行整理,求得抗震结构和隔震结构的阻尼矩阵。
图3和图4分别为抗震结构和基础隔震结构的顶层层间位移的均值和标准差曲线。图5为基础隔震结构隔震层位移均值和标准差曲线。对比图3和图4可以看出,基础隔震结构顶层层间位移的均值和标准差曲线峰值均小于抗震结构,对比图4和图5,可以发现基础隔震结构的隔震层发生相对较大的位移。为进一步分析,给出抗震结构和基础隔震结构每层的层间相对位移均值,如表2所示。
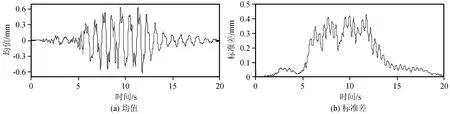
图3 抗震结构顶层层间位移均值和标准差曲线Fig.3 Curves of mean value and standard deviation of inter-story displacement at the roof of seismic structure
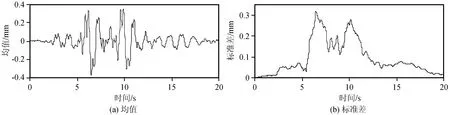
图4 基础隔震结构顶层层间位移均值和标准差曲线Fig.4 Curves of mean value and standard deviation of inter-story displacement at the roof of base isolation structure
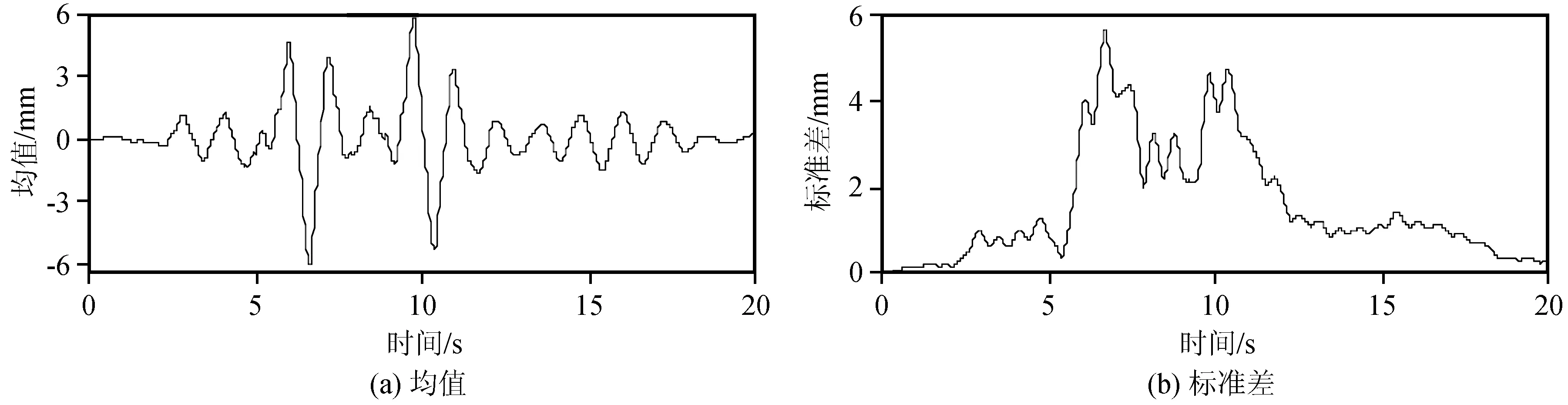
图5 基础隔震结构隔震层位移均值和标准差曲线Fig.5 Curves of mean value and standard deviation of displacement at isolation layer of base isolation structure
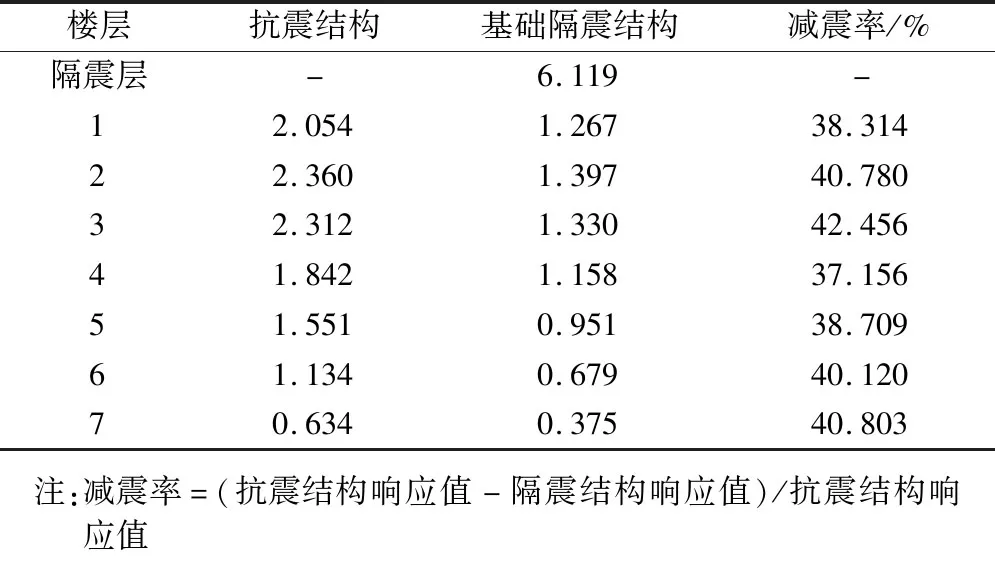
表2 抗震与基础隔震结构层间位移均值对比(单位:mm)Table 2 Comparison between inter-story displacement of seismic and base isolation structures (Unit:mm)
从表中可以看出,两种结构的最大层间位移均值发生在第二层,越往上楼层的层间位移越小,说明结构的第二层相对薄弱。基础隔震体系的上部结构每层的层间位移均值小于抗震结构,最大减震率达到了42.46%,而隔震层发生了较大的水平位移,说明设置了橡胶隔震支座后,结构的变形主要集中在隔震层,上部结构的响应减小。
图6为两种结构顶层的加速度对比图,从图中可以看出,设置了隔震层的结构顶层加速度峰值明显小于抗震结构,说明减震效果良好。图7和图8分别为两种结构顶层层间位移的概率密度函数(PDF)演化曲面图与等概率密度线。为了更加清楚地展现概率演化过程,图中只截取了某个时间段内的概率信息。从图中可以看出,概率密度演化方法能够准确地计算得到结构响应的概率密度信息,这是以往其他传统随机振动分析方法很难实现的。概率密度演化曲面从整体上直观地反映了结构随机响应概率密度的变化趋势及其大小;等概率密度曲线实质上为概率密度曲面的等高线,它可以直观地反应位移概率密度分布的范围及其变化走向,也可以反映出在每一条等概率线上层间位移随着时间的演化过程。对比图7和图8可以看出,基础隔震结构顶层层间位移的概率密度演化曲面变化相对于抗震结构更加均匀,且在峰值处更加集中。这也是其标准差相比抗震结构较小的缘故,隔震措施能有效减小结构响应的离散型。
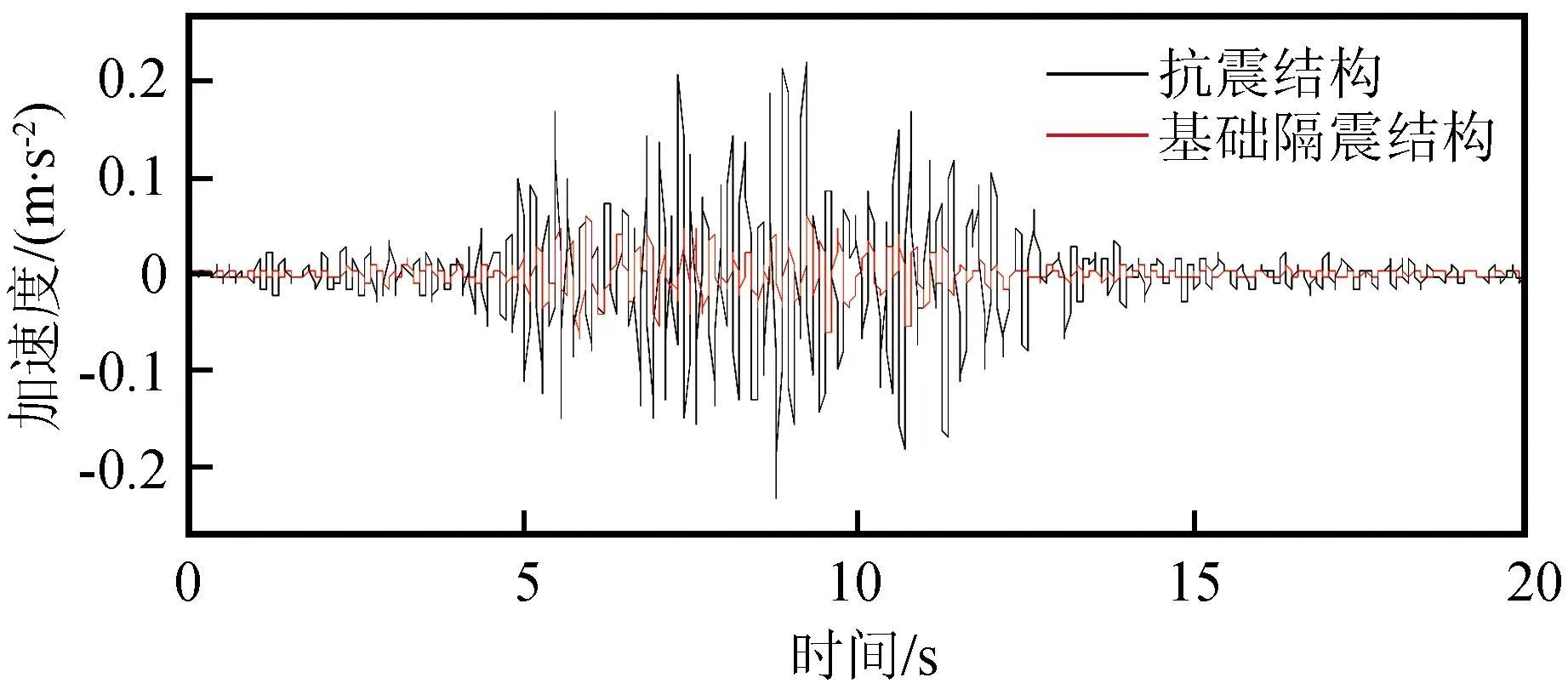
图6 结构顶层加速度均值对比图Fig.6 Comparison diagram of average acceleration at the roof of two structures
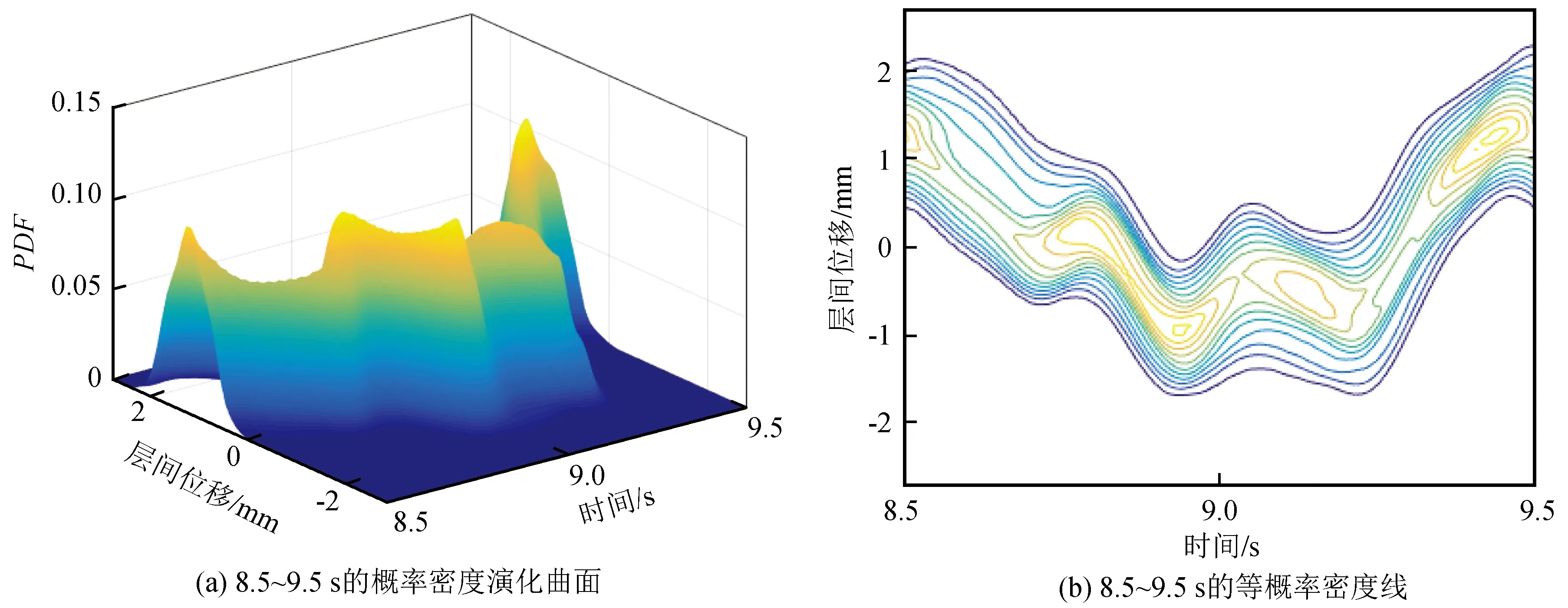
图7 抗震结构顶层层间位移的概率信息Fig.7 Probability information of inter-story displacement at the roof of the seismic structure
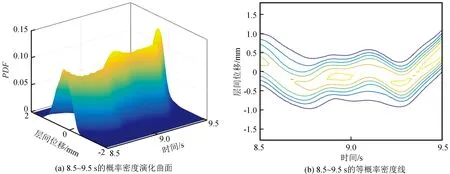
图8 基础隔震结构顶层层间位移的概率信息Fig.8 Probability information of inter-story displacement at the roof of the base isolation structure
图9为两种结构典型时刻顶层层间位移的概率密度函数曲线,从图中可以看到,基础隔震结构的顶层层间位移的分布范围比抗震结构要小,即顶层发生更小层间位移的概率大于抗震结构,表明基础隔震体系具有较好的减震效果。层间位移的概率密度曲线并不能用正态分布或其他常用分布函数表示,且随着时间发生不规则演变,因此传统随机振动方法在假定结构反应符合正态分布的基础上计算出来的二阶矩可靠度可能与实际工程结果存在一定的差距。
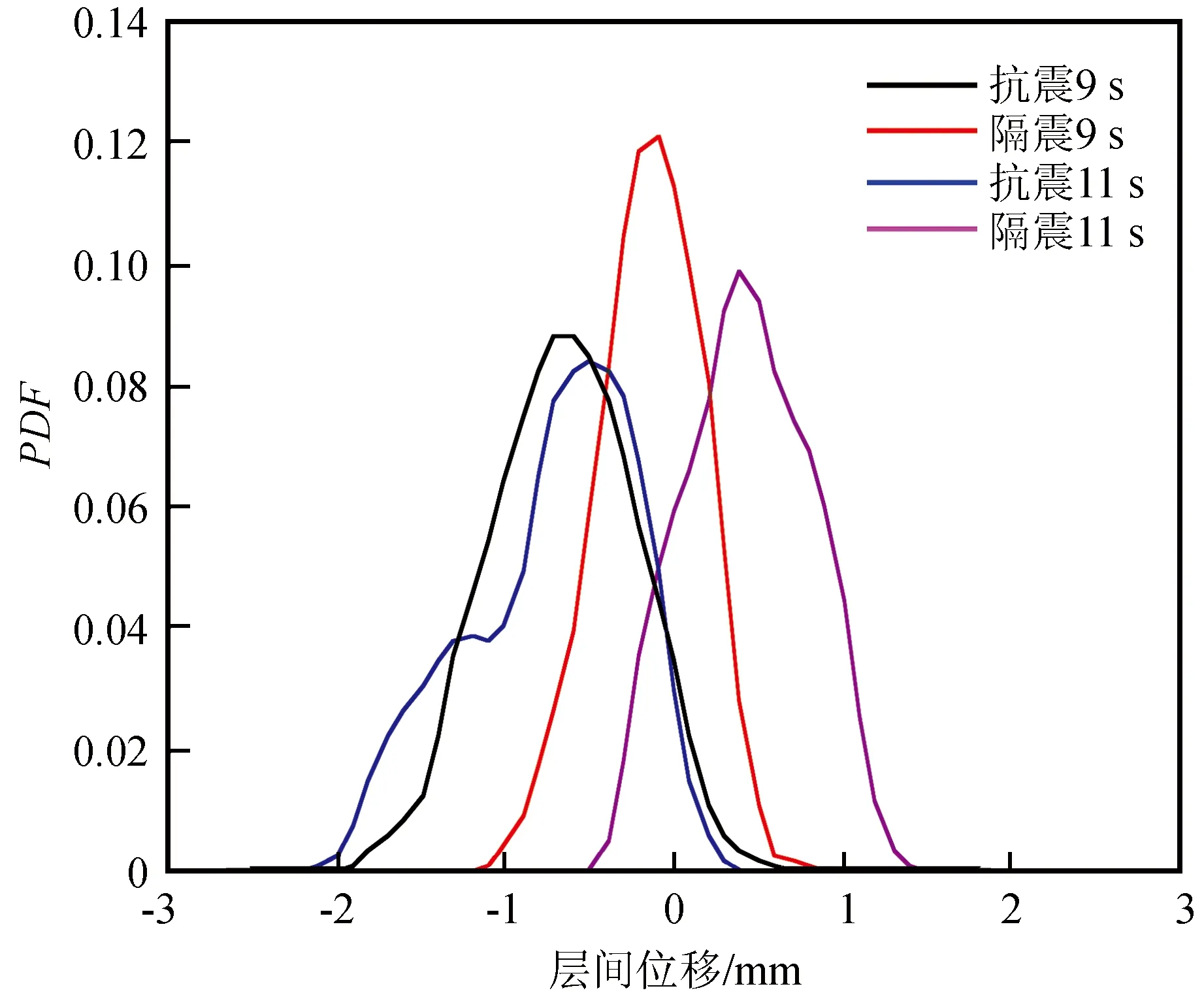
图9 典型时刻层间位移概率密度函数曲线Fig.9 The probability density function curve of inter-story displacement at typical moment
4 结论
本文基于概率密度演化方法,对抗震结构和基础隔震结构进行了随机地震作用下的线性随机响应分析,得到以下主要结论:
(1)对比抗震体系和隔震体系的层间位移响应均值可以发现,在随机地震作用下,隔震结构的隔震层发生了较大的变形,以此耗散地震能量,其上部结构的层间位移均值均小于抗震结构,且变化更加均匀,其减震率达到了42.46%。
(2)隔震层的设置能够减小结构位移响应的标准差,减少了结构响应的离散型。这表明基于概率密度演化方法计算的隔震体系在随机激励下相比抗震体系具有良好的减震性能。
(3)概率密度演化方法能够给出结构响应的完备概率信息。基础隔震结构的顶层层间位移的概率密度函数分布范围相比抗震结构较小,且相对峰值更加集中。位移响应的概率密度函数随着时间发生演化,其分布不能用正态分布或其他常用分布描述。
