基于地震记录的混凝土拱坝模态识别结果评价研究

武 璠,程 琳,杨 杰,郑东健

(1.西安理工大学 西北旱区生态水利工程国家重点实验室培育基地,陕西 西安 710048;2.河海大学水利水电学院,江苏 南 京210098)

0 引言

地震发生后,利用地震监测对结构模态参数进行识别,可以用来评估混凝土大坝抗震设计方案的合理性,修正数值模型和进行震损评估。因此,许多国家对大坝强震观测数据给予了高度重视。陈厚群[1]从1996—1998年中国758次水工建筑物强震记录中选取299份相关记录,并出版专著介绍这些强动记录。2008年汶川地震时,震区附近很多重要的大坝由于没有安装强震观测设备或者由于管理方面的问题,没有取得地震监测数据。这次地震后,我国颁布了混凝土坝安全监测技术规范(SL 601-2013),其中规定:“设计烈度为Ⅶ度及以上的1级大坝,或设计烈度为Ⅷ度及以上的2级大坝,应设置结构反应台阵”。近年来,国内新建的大型混凝土坝,如小湾、景洪、向家坝、龙滩、溪洛渡等,都按照要求安装了强震监测系统,以记录大坝的地震响应或者环境激励下的响应。日本大坝委员会(Japan Commission on Large Dam,JCOLD)收集整理了2000年至2012年日本各种大坝的5 649次强震观测,并专门出版了书籍[2]。自20世纪90年代以来,瑞士联邦水和地质局(Swiss Federal Office for Water and Geology,FOWG)启动了一项长期研究计划,通过在混凝土大坝上设置强震仪来研究混凝土大坝的动态特性[3]。在美国,加州地质调查局(California Geological Survey,CGS)加州强震仪计划、美国地质调查局国家强运动项目和先进国家地震系统(Advanced National Seismic System,ANSS)收集的强震记录可以搜索和下载[4-5]。葡萄牙国家土木工程实验室(Portuguese National Laboratory for Civil,PLNEC)开发了一种地震和结构健康监测系统,成功地应用于Cabril大坝、Baixo Sabor大坝和Cahora Bassa大坝的地震和环境振动监测和结构健康诊断[6]。在基于地震观测的混凝土坝模态识别方面,Loh等[7]首次将地震观测记录代入多输入单输出的自回归各态历经(Autoregressive Exogenous,ARX)模型识别Fei-Tsui拱坝的阻尼比、固有频率和传递函数,然后由环境激励试验确定振型;随后,Loh等[8]利用ARX模型研究了不同水位对拱坝频率和阻尼比的影响;Okuma等[9]根据Mauvoisin拱坝和Hitsuse拱坝的振动测试数据,采用频域法对两座拱坝进行了模态识别;Alves等[10]利用Pacoima拱坝记录到的两次地震数据识别出模态参数,并用有限元模型验证了此识别结果的有效性;练继建等[11]利用随机子空间法识别出二滩拱坝的模态参数;Yang J等[12]基于地震数据用ARX模型识别二滩拱坝的模态参数;李帅等[13]利用永善县两次地震记录和环境激励数据,分别采用带外源输入的自回归ARX模型、随机子空间法(Stochastic subspace identification,SSI)和频域分解法(Frequency Domain Decomposition,FDD),识别了溪洛渡拱坝的模态参数。目前针对拱坝这类水工混凝土结构的模态识别已经由理论探索到工程实践中,但仍缺少对各类方法的比较研究。如何根据工程实际情况,采取合适的方法进行模态识别,研究各方法的差异和产生差异的原因,为抗震分析等后续工作提供更为准确的结果仍是未来研究的重点。

鉴于此,本文选取龙羊峡拱坝作为工程实例,基于地震记录对混凝土拱坝模态参数识别问题进行对比研究。首先用龙羊峡拱坝两次地震观测数据,分别采用输入输出(Input-Output,IO)和仅考虑输出(Output-Only,OO)的模态识别方法,识别龙羊峡拱坝的模态参数,并对其进行比较和研究分析差异产生的原因,评价其优劣性,为基于地震记录的混凝土拱坝模态参数识别方法的选择和系统识别结果的分析提供参考。

1 拱坝模态识别的基本原理

在结构模态识别中,一般假定结构系统为线性时不变系统(Linear and Time-invariant,LTI),这意味着系统参数不随时间变化。从模型的建立方式分类,这些模态识别方法可分为考虑输入和输出的IO法和仅考虑输出的OO法。IO型识别方法将坝基自由场的地震记录作为模型输入,坝上地震反应记录作为模型输出,从本质上说,地基被认为是刚性的,地震运动以支持激励的形式应用于坝体,其中ARX模型和FDD是常用的识别方法。OO型识别方法以坝基自由场和坝体地震监测数据为输入,其中ERA和SSI是比较常用的识别方法。以分别介绍对这几种方法的基本原理进行介绍。

1.1 ARX模型

具有多输入/单输出(MISO)的ARX模型定义如下[14]:

A(q)y(t)=B1(q)u1(t-nk1)+...+

Bnuunu(t-nknu)+e(t)

(1)

式中:y(t)表示单个输出;ui(t)表示第i个输入;nki表示系统中从输入到输出的延迟;nu是输入的数目;A(q)和Bi(q)分别是na阶和nbi阶多项式;e(t)表示噪声干扰。

通过使上述模型预测的结构地震响应与实测地震响应之间的误差最小化,可以求解模型的系数。这时可以采用式(2)求解系统输入ui(t)与系统输出y(t)之间的传递函数。

(2)

在得出方程(2)分母中多项式的根后,可以用下列方程得到结构频率fk和阻尼比ξk。

(3)

式中:Re(ln(qk))为复数|ln(qk)|的实部;qk是分母多项式的根。

1.2 频域分解法(FDD)

频域分解法是一种频域算法[15-17],若输入为白噪声,则输出响应信号的功率谱密度函数Gyy(jω)可表示为:

Gyy(jω)=H*(jω)Gxx(jω)HT(jω)

(4)

式中:Gxx是输入信号功率谱矩阵;H(jω)是频率响应函数矩阵,上标*表示伴随矩阵,上标T表示转置矩阵。在第m阶模态处,式(4)可以简化为

(5)

式中:φm为第m阶振型;diag(·)为对角矩阵;cm为实数标量;λm为第m阶极点。

根据各通道测量的响应信号,估计各信号的频谱和频谱密度,然后进行奇异值分解。

(6)

对结构响应功率谱密度矩阵进行奇异值分解得到奇异值谱曲线,在某个峰值处,若仅第m阶模态起控制作用,则结构的第m阶振型的估计值可以通过最大奇异值对应的酉向量Ur得到。

1.3 特征系统实现算法(ERA)

n自由度结构振动的平衡方程可以表达为“确定-随机”离散状态空间模型的形式。

(7)

式中:zk和yk分别为系统状态向量和观测向量;uk为系统激励;wk和vk分别是激励中的随机分量和观测噪声;A、B、C和D分别是离散系统矩阵、输入矩阵、观测矩阵和直接传递矩阵。

当系统的激励可以用高斯白噪声来代替时,模型可用下式表示:

(8)

(9)

典型的ERA识别方法需要采用脉冲响应函数(Markov parameters)来构造Hankel矩阵,但脉冲响应很难直接获取,可以采用自然激励技术(NExT)来获取,如ERA-NExT和ERA-NExT-AVG。ERA-OKID-OO 和ERA-OKID-IO是基于Kalman滤波(OKID)方法的ERA改进版本。

1.4 随机子空间识别法(SSI)

随机子空间识别是一种时域模态参数识别方法,假设外部激励为白噪音,利用随机状态空间模型求解结构模型参数。结构随机状态空间模型由以下方程[18]表示:

(10)

式中:Xk是离散状态向量;Yk是输出向量;A是系统状态矩阵;C是输出矩阵;Wk和Vk分别是表示环境激励和模型误差引起的噪声以及传感器误差引起的测量噪声之和,假定为互不相关且均值为零的白噪声。

SSI-cov方法是基于测量结构响应时间的协方差矩阵,可由以下式获得:

(11)

式中:N是时间序列的点数,上标T表示转置。

(12)

矩阵A和C的识别是从这个矩阵执行的(一些算法包括在识别之前加权矩阵的应用,但这些在这种情况下没有使用)。该方法的算法基于随机系统的性质[19],涉及一个奇异值分解和一个最小二乘方程的解。对状态空间模型进行辨识后,从矩阵A和矩阵C[20]中提取模态参数。

2 混凝土拱坝模态识别的工程经验

表1是国内外部分混凝土拱坝基于强震记录进行模态参数识别结果的统计。

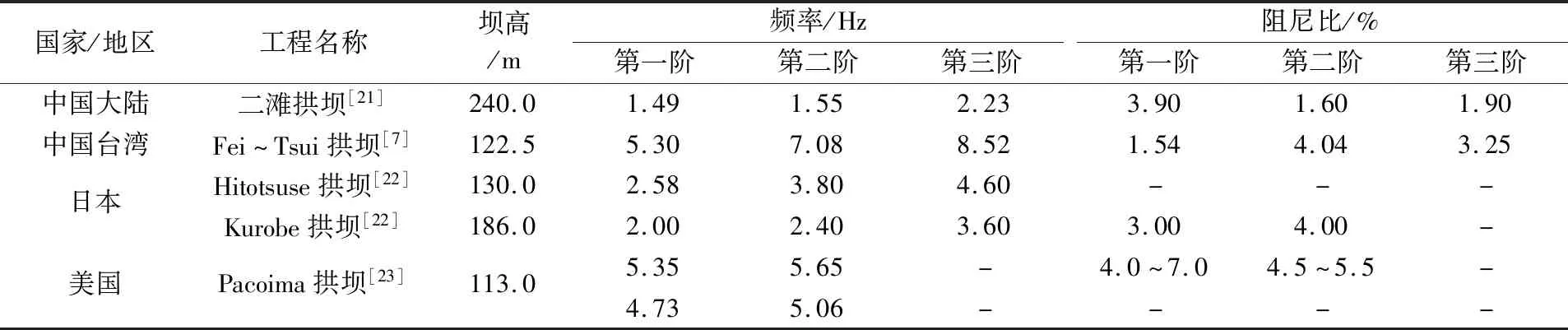
表1 国内外部分混凝土拱坝基于强震记录的模态识别结果Table 1 Modal identification results of some concrete arch dams at home and abroad based on strong earthquake records

Okamoto[24]在总结混凝土拱坝原型振动试验的基础上,得出坝体基本自振周期T和坝高H的经验关系式为:

(13)

寇立夯等[22]对40座拱坝利用原型观测识别的模态参数进行回归分析,得到的结构基本自振周期T和坝高H的回归方程如下:

(14)

3 龙羊峡拱坝及其强震观测

龙羊峡大坝是一座178 m高的混凝土拱坝,1986年建成。龙羊峡是黄河上游七座梯级大坝中的第一座大坝。如图1所示,拱坝的拱形段长396 m,坝顶和坝基厚度分别为15 m和80 m。大坝还包括两个30 m高的混凝土重力砌块,在拱顶两端都设有辅助坝。大坝包括右侧坝肩上的溢流溢洪道、底部附近右侧的两个较低的出口和左侧桥台附近中间高度处的一个中间出口。

图1 龙羊峡拱坝[25]Fig.1 Longyangxia arch dam[25]

该强震监测系统分布有13个观测点(坝内12个观测点,1个自由场点),共39个监测分向,测点沿拱冠梁从坝顶到坝基、1/4拱圈处,坝肩布置,拱坝的拱座沿不同高度、河谷自由场布置,传感器测量方向为坝体的水平径向、水平切向和竖向三分量,强震系统测点分布见图2。

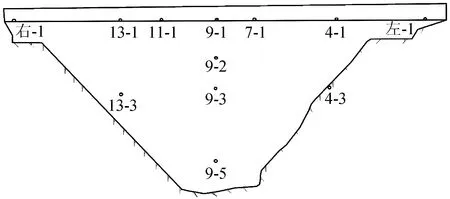
图2 龙羊峡拱坝强震系统测点分布图Fig.2 Distribution of measuring points of strong earthquake system at Longyangxia arch dam

本文采用的龙羊峡地震记录来自国家地震科学数据中心。自1990年青海唐格木地震至1994年,龙羊峡强震台阵取得的地震记录8次(表2),虽然记录到的加速度值不是很大,但是由于龙羊峡水工台阵的布设特点和记录完整性,使记录的分析价值大大增加。

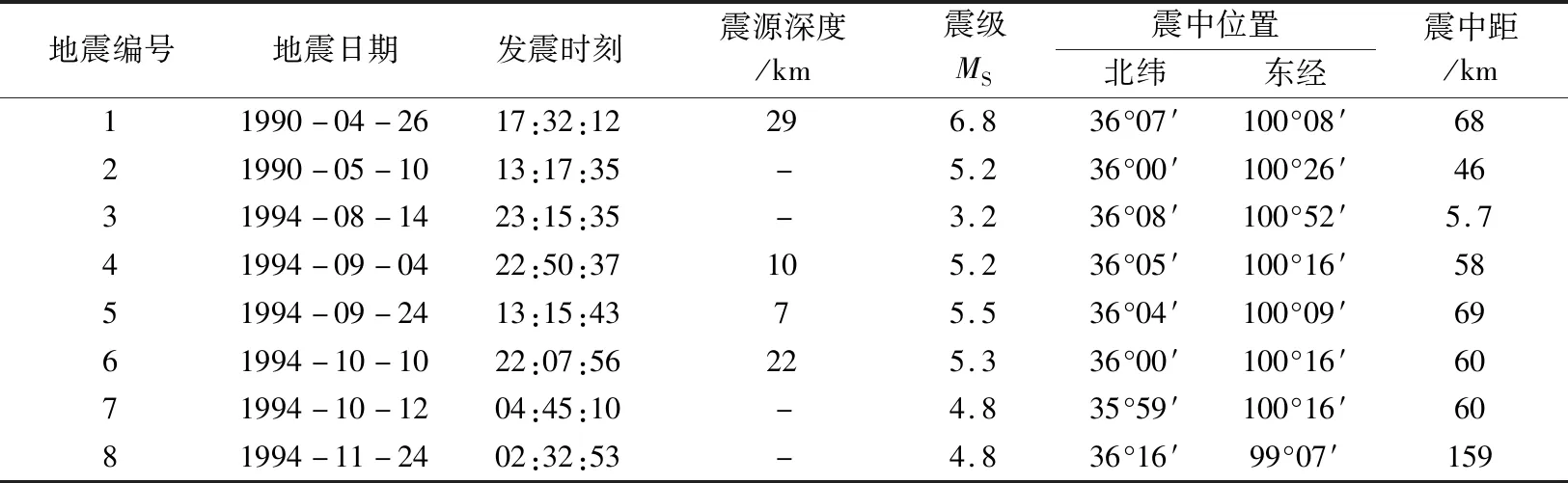
表2 地震参数记录Table 2 Seismic parameters

在龙羊峡的地震记录中,以1994年8月14日和10月10日两次地震的记录较为完整,可较好的表现两岸坝肩和坝基的地震反应特性。因此本文选取这两次地震记录进行模态参数识别。图3为地震激励下各通道的实测地震激励响应。由于观测通道数量较多,限于篇幅,本文仅给出1994年8月14日地震激励下,测点位置分别为9-1(切向)、9-5(切向)、右1重力墩(切向)、11-1(切向)的实测地震激励响应图及其对应的功率谱图(图4)。地震观测数据的采样频率f=60 Hz。

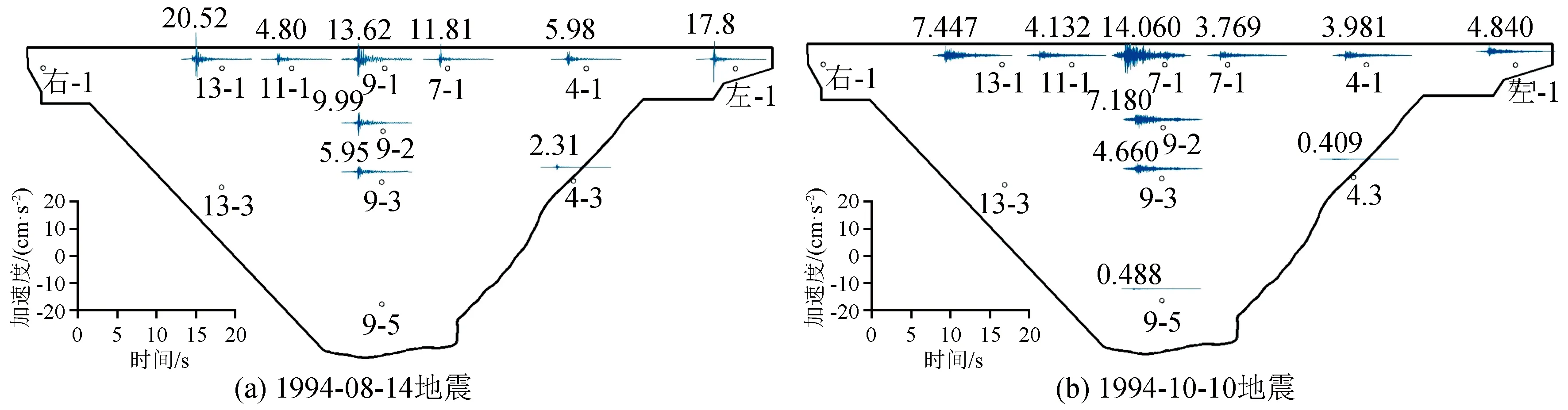
图3 龙羊峡拱坝在两次地震激励下各通道的实测地震激励响应Fig.3 Measured seismic response of each channel of Longyangxia arch dam under two seismic excitations

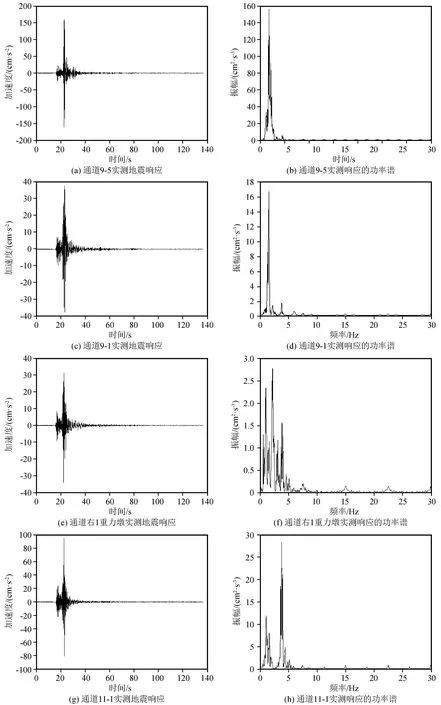
图4 不同测点实测地震激励响应及其对应的功率谱图Fig.4 Measured seismic response and corresponding power spectrum at different measuring points

4 频率和阻尼比识别结果分析

选取龙羊峡拱坝作为工程实例,分析识别方法不同对混凝土拱坝模态识别结果产生的影响,并分析了不同类型方法识别结果差异产生的原因。考虑激励方式、识别方法、地震强度等因素对模态识别结果的影响。

4.1 OO型方法识别结果

使用坝体和坝基的所有地震监测通道数据和一些OO型方法确定的前5阶频率和阻尼比(表3),利用坝体地震监测通道数据识别的前5阶频率和阻尼比(表4)。图5是采用1994年10月10日地震记录进行模态识别时,两种不同识别方法对应的稳态图。

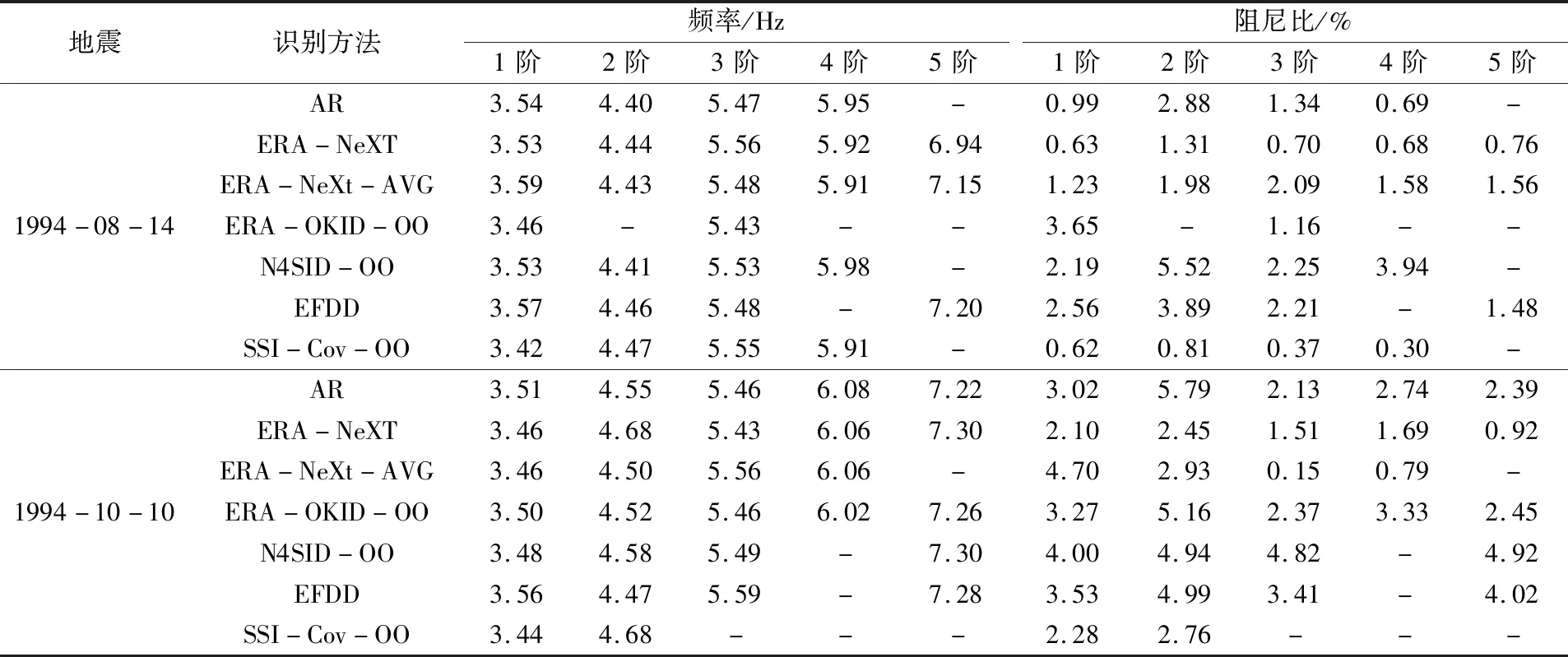
表4 仅采用坝体地震观测通道监测数据和OO类方法识别的频率和阻尼的识别结果Table 4 Identification results of frequency and damping by using the monitoring data of dam body observation channel (OO method)

(1)由表3可以看出,使用坝体和坝基的所有地震监测通道数据识别时,得到1994年8月14日地震的基频在3.2～3.6 Hz之间,1994年10月10日地震的基频在3.4～3.6 Hz之间。对比在同一次地震下采用不同识别方法得到的结果,其整体差异不大。以1994年8月14日地震为例,ERA-NeXT方法识别出来的基频最小,为3.28 Hz,而ERA-OKID-OO方法识别出来的基频最大为3.59 Hz,两种方法结果的差值为0.31 Hz。而对比两次地震使用同种方法识别时,以AR方法为例,两次地震第二、三阶频率的差值分别为0.16 Hz、0.11 Hz,其差异并不大。不同地震激励时,结构频率的识别结果差异存在。说明不同地震对大坝的动力特性影响各不相同,而产生差异的主要原因可能是在不同的地震作用下,地震的震级和峰值存在差异,从而产生的拱坝横缝张开的程度、地基基岩断层的错动情况以及地震的非线性都不相同。

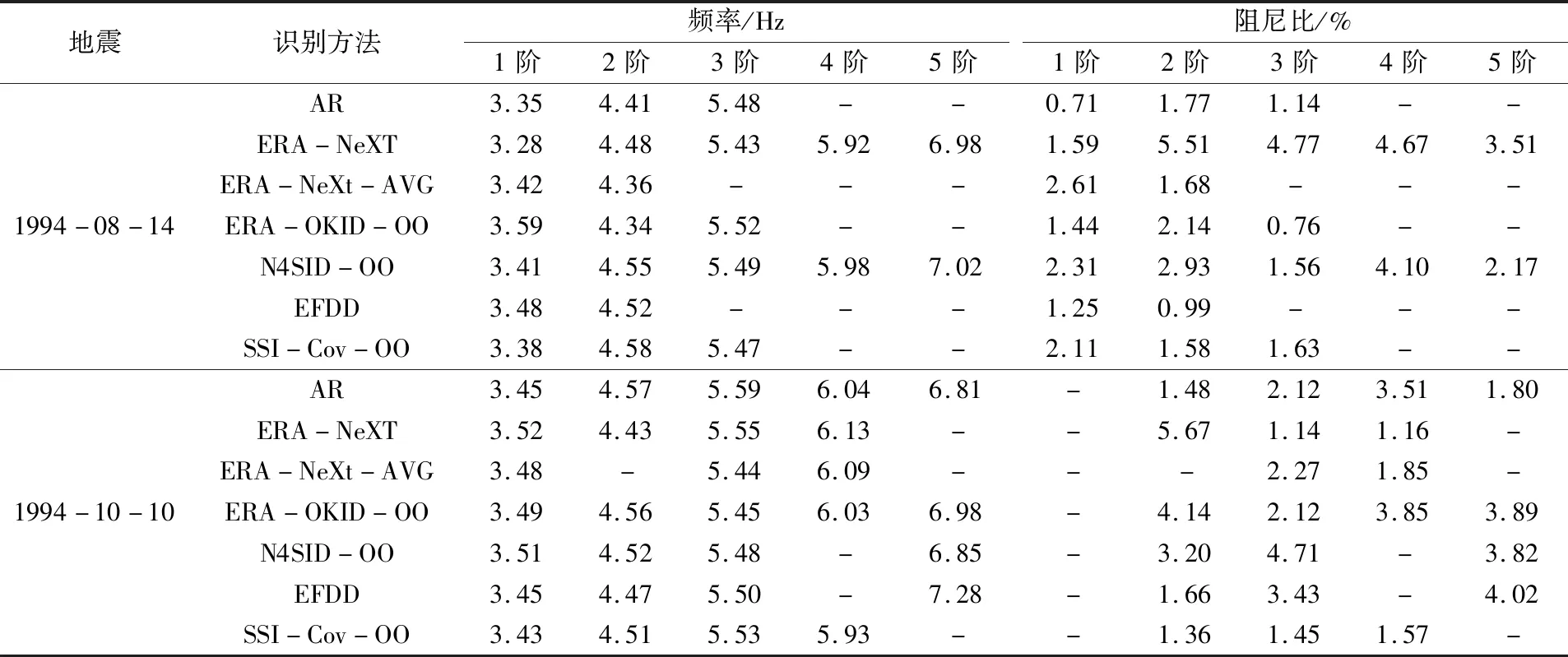
表3 采用所有地震观测通道的监测数据和OO类方法识别的频率和阻尼的识别结果Table 3 Identification results of frequency and damping by using the monitoring data of all seismic observation channels (OO method)

(2)由表4可以看出,仅利用坝体地震监测通道数据识别时,得到1994年8月14日地震的基频在3.4～3.6 Hz之间,1994年10月10日地震的基频在3.4～3.6 Hz之间。对比在同一次地震下采用不同识别方法得到的结果,其整体差异也不大。以1994年10月10日地震为例,前三阶频率的最大差值分别为0.12 Hz、0.21 Hz、0.16 Hz,均在0.3 Hz以内。

(3)对比表3和表4可以看出,同一次地震使用不同的监测数据进行识别时,以1994年8月14日地震为例,使用SSI-Cov-OO方法得到的频率差值最小,为0.04 Hz。使用ERA-NeXT方法得到的频率差值最大,为0.25 Hz。所以在同一次地震下采用不同监测数据得到的结果,其整体差异也不大。

4.2 IO型方法识别结果

采用坝基观测通道监测数据作为非均匀输入,坝体地震观测通道监测数据作为输出和IO类方法识别的频率和阻尼的识别结果如列于表5。采用坝基顺河向观测通道监测数据作为非均匀输入,坝体顺河向观测通道监测数据作为输出的频率和阻尼识别结果列于表6。图6是基于1994年8月14日地震记录下,不同识别方法在同一阶下的频率结果对比图。

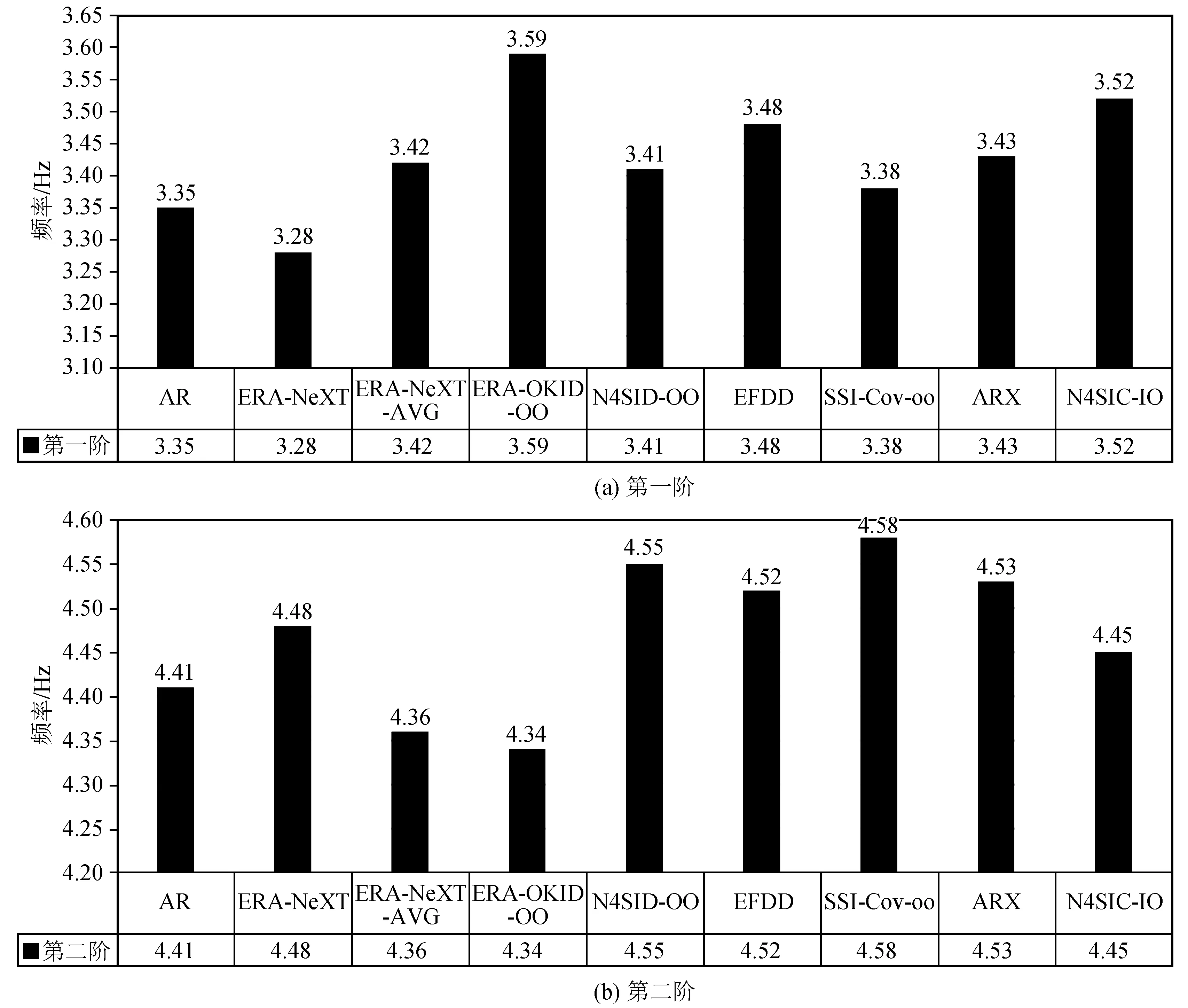
图6 基于1994年8月14日地震记录下,不同识别方法在同一阶下的频率结果对比图Fig.6 Comparison of frequency results of different recognition methods in the same order based on the earthquake records on August 14,1994

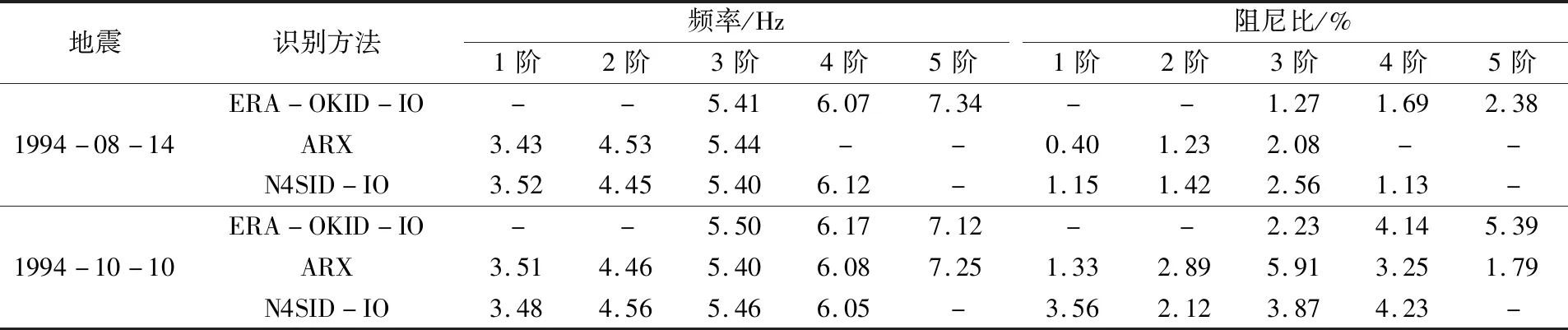
表5 坝基观测通道监测数据作为非均匀输入,坝体地震观测通道监测数据作为输出和IO类方法识别的频率和阻尼的识别结果Table 5 Identification results of frequency and damping by using monitoring data of dam foundation observation channel as non-uniform input and data of dam body observation channel as output (IO method)

(1)对比表3～表6可以看出,对于相同的地震监测,采用OO类识别方法可以识别出更多模态。由于坝基对应的模态参数(而不是坝体的模态频率)和地震波的主导频率可能被识别,因此确定如何消除地震波的主导频率是至关重要的。

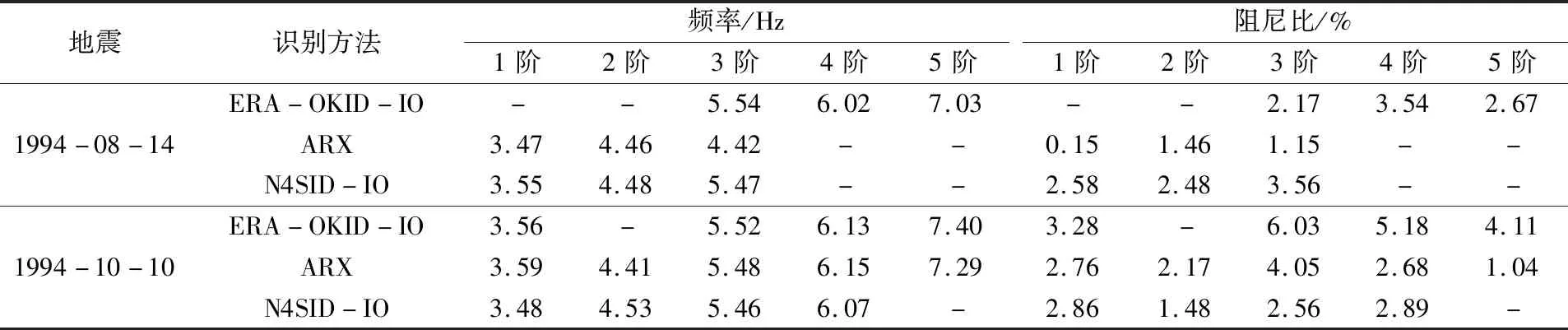
表6 坝基顺河向观测通道监测数据作为非均匀输入,坝体顺河向观测通道监测数据作为输出的频率和阻尼识别结果Table 6 Identification results of frequency and damping by using monitoring data of dam foundation observation channel along the river as non-uniform input and data of dam body observation channel along the river as output

(2)对比IO类识别方法与OO类识别方法,以1994年10月10日地震为例,OO类识别方法得到的基频在3.2～3.6 Hz之间,IO类识别方法得到的基频也在这个范围内。对比AR与ARX方法,识别出来的前三阶频率的差值分别为0.08 Hz、0.12 Hz、0.04 Hz,均在0.2 Hz以内,其差异并不大。基于相同的地震记录,从各种识别方法得到的相同阶次频率差异不大。对比表4～表7中识别出来的阻尼比,可以看出阻尼比的系统识别结果差异较大,这主要是由于大坝结构阻尼特性的高复杂度所致。基于震动强烈的1994年10月10日地震识别的阻尼比1994年8月14日地震识别结果要大,说明强烈地震作用时,拱坝的能量耗散更为显著。

4.3 与工程经验及其他学者研究成果的对比

利用经验公式(13)可以得到龙羊峡第一阶频率为2.193 Hz;利用经验公式(14)可以得到龙羊峡的前三阶频率分别为2.124 Hz,2.537 Hz,3.251 Hz。将这两种经验公式得到的结果与本文得到的识别结果进行对比,经验公式得到的结果值普遍偏小,这可能与大坝的低阶频率未被激励出来有关。一些学者获得的龙羊峡拱坝动力分析识别结果列于表7。

(1)由表7可以看出,模型试验时,满库下测得的频率都小于空库下。有学者认为,库水位在60%最高水位以下时,自振频率基本不变;库水位超过60%最高水位以后,自振频率会随着附加质量的增加而减小[21]。可能是因为随着水位的增加,一方面拱坝的横缝被压紧,整体刚度增加;另一方面,库水附加质量随着水位的升高而增大。开始时,刚度的增加对自振频率的影响超过了附加质量的增加所带来的影响,自振频率升高到一定水位以后,附加质量的增加带来的影响开始占主要地位,因此会出现频率先增加后减小的现象。

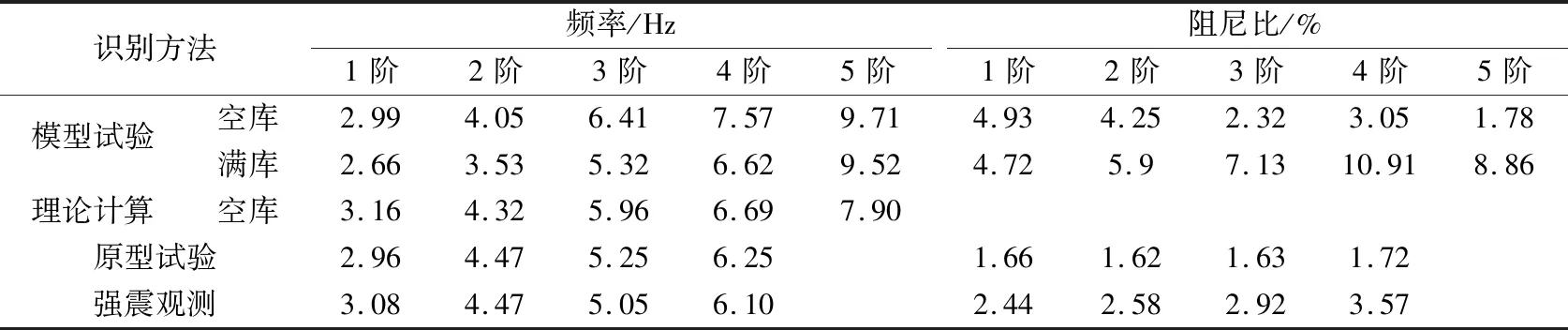
表7 龙羊峡拱坝其他动力分析结果比较[26]Table 7 Comparison of other dynamic analysis results of Longyangxia arch dam[26]

(2)结合本文成果和已有成果来看,阻尼比与自振频率没有明显的相关关系,但与激励强度有关。根据两次地震观测数据的对比,地震作用下激振能量很大,坝体和地基材料会进入非线性状态,拱坝横缝也可能反复张开、闭合,坝体还会发生局部开裂等,都会引起更多的能量耗散,拱坝在强烈地震作用下的阻尼有可能更大。

5 振型识别结果的分析

图7是2次地震分别利用ERA-OKID-OO、SSI-Cov-OO、ARX 3种方法计算的第一阶振型以及其同一地震下两两振型对比的模态置信(MAC)值。

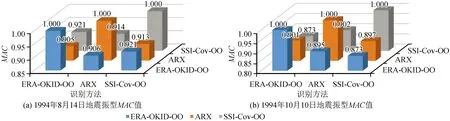
图7 采用不同方法识别的第一阶振型的对比Fig.7 Comparison of the first modes identified by different methods

图8是2次不同地震利用ERA-OKID-OO、SSI-Cov-OO与ARX 3种方法计算的第一、二阶振型图,以及其相应的MAC值,其中图8(a)、(b)为1994年8月14日地震前两阶振型图,图8(c)、(d)为1994年10月10日地震前两阶振型图。

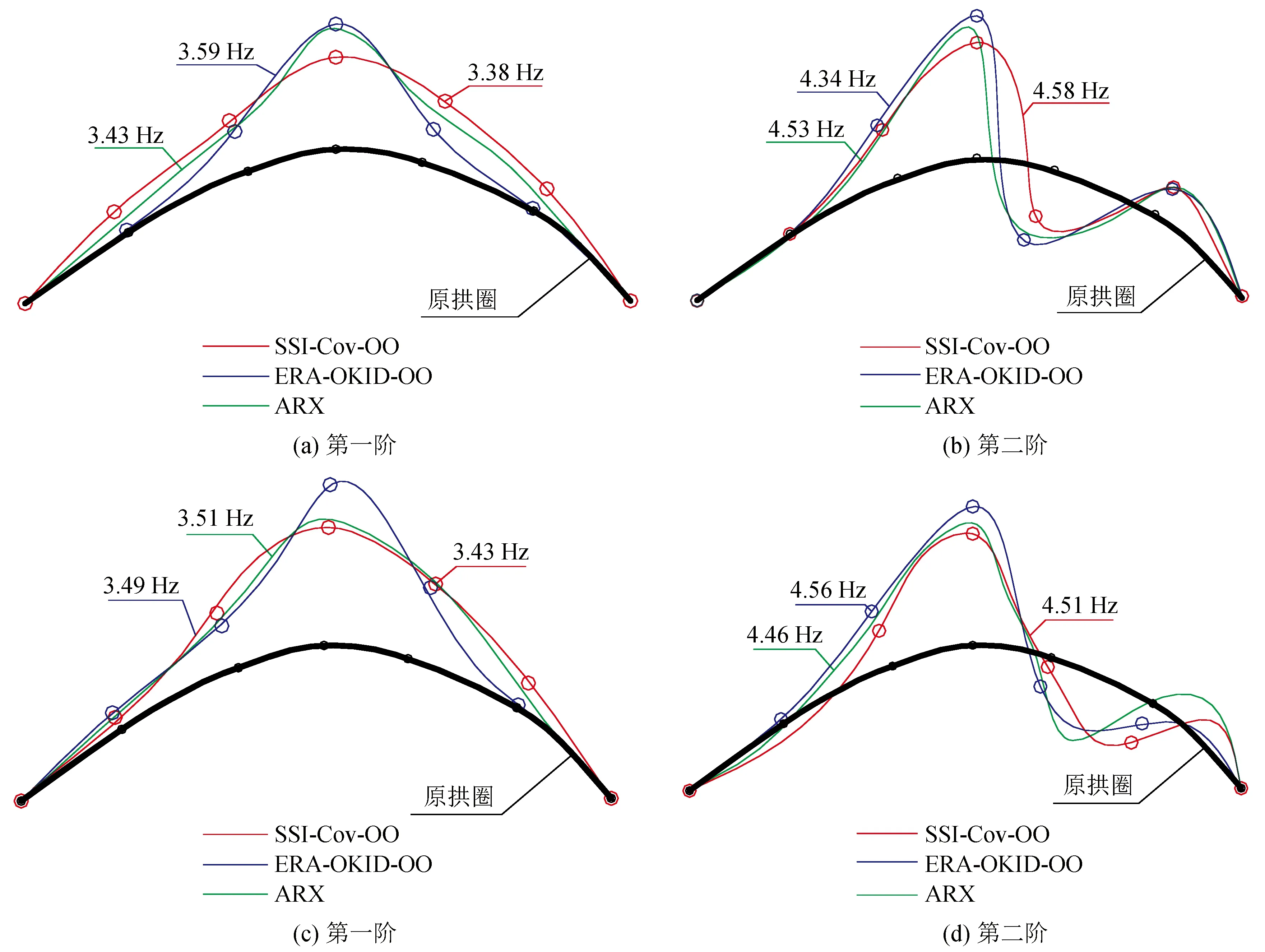
图8 第一、二阶振型图和相应MAC值Fig.8 The first and second mode shapes and corresponding MAC values

在2次不同地震观测振型计算中,1994年8月14日地震的MAC较大,均在0.9以上,1994年10月10日地震的计算振型MAC值均不到0.9。1994年8月14日地震的振型计算结果较为理想。

6 结论

本文利用龙羊峡拱坝的不同地震观测数据,分别采用ARX,FDD,ERA和SSI方法进行模态参数识别,结合其他学者不同的识别结果,分析不同方法模态参数识别结果产生差异的原因,评价各种模态识别方法的优劣性,结论如下:

(1)不同地震模态参数识别结果不同,说明不同地震对大坝的动力特性影响各不相同。产生差异的主要原因可能是在不同的地震作用下,地震的震级和峰值存在差异,从而产生的拱坝横缝张开的程度、地基基岩断层的错动情况以及地震的非线性都不相同。

(2)OO型方法一般可以识别更多的阶模。一些OO型模态识别方法在很大程度上取决于激励是稳定的假设。然而,地震波是不稳定的,违反这一假设将降低模态识别结果的准确性。基于相同的地震记录,从各种识别方法得到的相同阶次频率差异不大。而阻尼比的系统识别结果差异很大,这主要是由于大坝结构阻尼特性的高复杂度所致。

(3)在强烈的地震作用下,拱坝能量的耗散更为显著。地震作用下激振能量很大,坝体和地基材料会进入非线性状态,拱坝横缝也可能反复张开、闭合,坝体还会发生局部开裂等,都会引起更多的能量耗散,拱坝在强烈地震作用下的阻尼比可能更大。