隔震与非隔震支座对混凝土箱梁桥 地震易损性的影响

方圣恩,唐永久

(1.福州大学 土木工程学院,福建 福州 350108;2.福州大学 土木工程防震减灾信息化国家地方联合工程研究中心,福建 福州 350108)

0 引言

截至2019年底,我国公路桥梁已超过87万座,大部分是中小跨径梁桥,其中混凝土连续梁桥有着很大占比。近年来随着隔震技术的不断发展和成熟,越来越多的公路桥梁开始使用隔震技术以降低地震作用造成的桥梁破坏[1]。在隔震桥梁设计时,需要选用合适减震措施来达到最大的减震效果,而为了定量分析减震的程度,比较直观的方式就是评估隔震与非隔震桥梁的地震易损性。

桥梁地震易损性是指桥梁结构在地震作用下发生不同破坏状态的超越概率,一般采用地震易损性曲线来表征[2],国内外对于隔震桥梁与非隔震桥梁的地震易损性也进行了大量的研究[3-5]。文献[6]以概率性地震需求分析模型研究了隔震与非隔震连续梁桥的地震易损性,分别采用墩顶最大位移和支座相对变形作为桥墩和支座的损伤指标,在构件层面上建立了桥墩和支座的地震易损性曲线,发现相对于非隔震桥梁,隔震桥梁表现出良好的抗震效果。文献[7]建立了铁路桥梁轨道、主梁、隔震支座以及桥墩共同作用的有限元模型,分析桥梁的弹塑性地震时程响应,并基于位移破坏准则提出了一种E型钢阻尼支座损伤指标的确定方法,以较好地评价支座的破坏状态和超越概率。文献[8]以一座隔震连续梁桥为对象,基于OpenSees建立数值分析模型,构建了桥梁各构件间的响应面模型,分别以位移延性比和支座剪应变作为桥墩和支座的损伤指标,发现隔震支座可以有效地减少桥墩的破坏概率。此外,文献[6-8]采用位移延性比作为桥墩损伤指标,从而建立隔震桥梁地震易损性曲线。

为了从不同桥墩损伤指标角度来分析隔震桥梁地震易损性,笔者之前针对桥墩提出了转角延性比损伤指标[9]。本文为进一步深入分析隔震与非隔震支座对桥梁抗震性能的影响,以隔震铅芯橡胶支座和非隔震型盆式支座的剪应变作为支座损伤指标,采用50条实测地震波作为输入,求得一座混凝土连续箱梁桥在不同类型支座和破坏状态下的超越概率,并通过一阶界限法建立隔震和非隔震桥梁的全桥系统地震易损性曲线,以此研究隔震支座对桥梁地震易损性的影响。

1 桥梁地震易损性曲线

1.1 桥梁构件地震易损性曲线

桥梁地震易损性分析首先要求得构件的地震响应,再根据损伤评定方法处理所求的构件地震响应,最终得到桥梁系统(全桥)的地震易损性曲线[2],其间一般假定地震易损性曲线为累计对数正态分布形式。地震易损性曲线的建立通常采用可靠度法和数值模拟方法[10],本文有效结合两种方法,基于一阶可靠度理论和OpenSees数值分析模型,建立桥梁构件(桥墩和支座)以及全桥的地震易损性曲线。

在结构地震易损性曲线的构建过程中,首先要确定地震动参数IM和对应的地震需求Sd之间的关系,再对二者取对数并回归分析[11]:

lnSd=lna+blnIM

(1)

式中:a和b为回归系数;Sd取为地震需求的中位值,与IM成对数线性关系。在某种强度地震动作用下,结构的地震需求服从对数正态分布,故概率地震需求模型可表示为:

(2)

式中:Φ(·)为标准正态分布函数;βSd|IM为地震需求的对数标准差;Sc为结构抵抗破坏状态能力的中位值。进行构件层次的地震易损性分析时,可假定构件的极限抗力服从对数分布,因此综合式(1)、(2)可得地震易损性曲线计算公式:

(3)

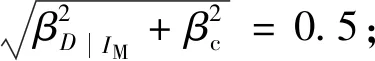
1.2 桥梁系统地震易损性曲线

桥梁系统的破坏概率比单个构件如桥墩或支座的破坏概率往往要大[13],因此在得到构件的地震易损性后,进一步分析全桥地震易损性是十分必要的。假设桥梁为串联结构系统,即各构件间易损性影响是独立的,就可采用一阶体系的上下界来计算桥梁系统的地震易损性曲线[14]:

(4)

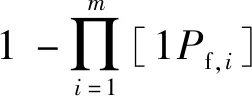
2 桥梁地震损伤指标

2.1 桥墩损伤指标

本文混凝土连续箱梁桥墩高15 m<40 m,根据《公路桥梁抗震设计细则(JTG/T B02—01—2008)》[15],属于规则桥梁。基于桥墩的弯矩转角性能曲线[16],笔者提出了墩底转角的损伤指标—“转角延性比”[9]:

(5)

式中:θ为墩底截面的转角;θy为墩底截面屈服时的转角。

为了确定不同转角所对应的破坏状态,参考文献[16](图1)中的Mθ骨架曲线,对转角延性比损伤指标定义轻微破坏、中等破坏、严重破坏和倒塌破坏4种破坏状态,具体评价指标见表1所列。其中θy为屈服转角,θIO为等效屈服转角,θLS为处于性能点的塑性转角,θr为失效点转角。同时θIO=θy+0.5(θp-θy),θLS=θp+0.5(θu-θp),其中θp为峰值转角,θu为极限转角[16]。由此可见,损伤转角延性比指标的量化是基于弯矩转角曲线得到,分别是从力(弯矩)和变形(转角)两个角度来评价桥墩的易损性水平。对于规则桥梁的一般桥墩而言,墩底截面的弯矩最大,因此可以基于墩底转角来构建损伤指标。

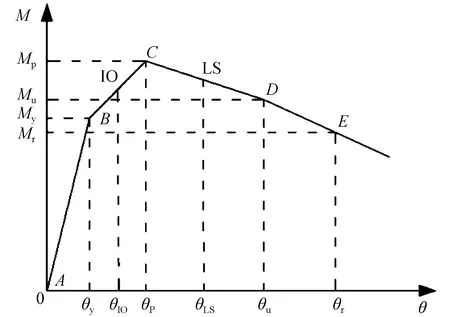
图1 RC墩柱M-θ曲线[16]Fig.1 M-θ curve for RC piers[16]

表1 破坏等级分类Table 1 Classification of damage levels

2.2 支座损伤指标

桥梁结构在遭受地震作用时,上部结构荷载会通过支座传递给桥墩结构,因此支座会产生很大的变形。一般情况下可采用支座变形作为支座破坏状态的定义。对于隔震铅芯橡胶支座可采用剪应变作为损伤指标,支座剪应变[17]定义见式(6):

(6)

式中:δ为铅芯橡胶支座的相对水平位移;∑tr为铅芯橡胶支座橡胶层总厚度。具体破坏指标分为5个范围:基本完好(γ<100%)、轻微破坏(100%≤γ<150%)、中等破坏(150%≤γ<200%)、严重破坏(200%≤γ<250%)、完全破坏(γ≥250%)。

对于算例中非隔震型的普通盆式支座,可参考规范《公路桥梁盆式支座(JT/T 391—2009)》[18],将支座相对位移作为损伤指标。目前对于非隔震型盆式支座的损伤指标量化研究很少,若桥梁的纵向位移过大,普通盆式支座容易发生破坏。本文研究主要针对纵桥向位移,故前文4种损伤指标的量化是基于支座的容许位移,所选取的非减震型普通盆式支座[GPZ8DX(SX,GD)±200]设计位移为±200 mm,同时根据规范规定的±50 mm允许偏差,结合规范[18]和文献[19]将50 mm和100 mm定义为轻微破坏和中等破坏的界限,严重和完全破坏时分别为150 mm和225 mm。

3 工程案例

3.1 工程概况及有限元模型

某三跨混凝土连续梁桥位于Ⅲ类场地上,上部结构为预应力箱梁,跨度为(30+50+30)m,主梁采用C50混凝土(轴心抗压强度32.4 MPa)。桥墩为1 m×1 m实心矩形墩,墩高为15 m,采用C40混凝土(轴心抗压强度26.8 MPa)。纵筋和箍筋都采用屈服强度为335 MPa 的HRB335级钢筋,纵筋为24Φ25的HRB335级钢筋,箍筋按螺旋筋配置,配箍率为0.96%。

本文采用OpenSees建立桥梁的有限元模型如图2所示。主梁在地震作用下一般不发生破坏,处于弹性状态,故主梁使用弹性单元模拟。由于墩柱可以发生一定的延性破坏,允许其进入弹塑性状态,因此采用纤维单元进行模拟(图2)。

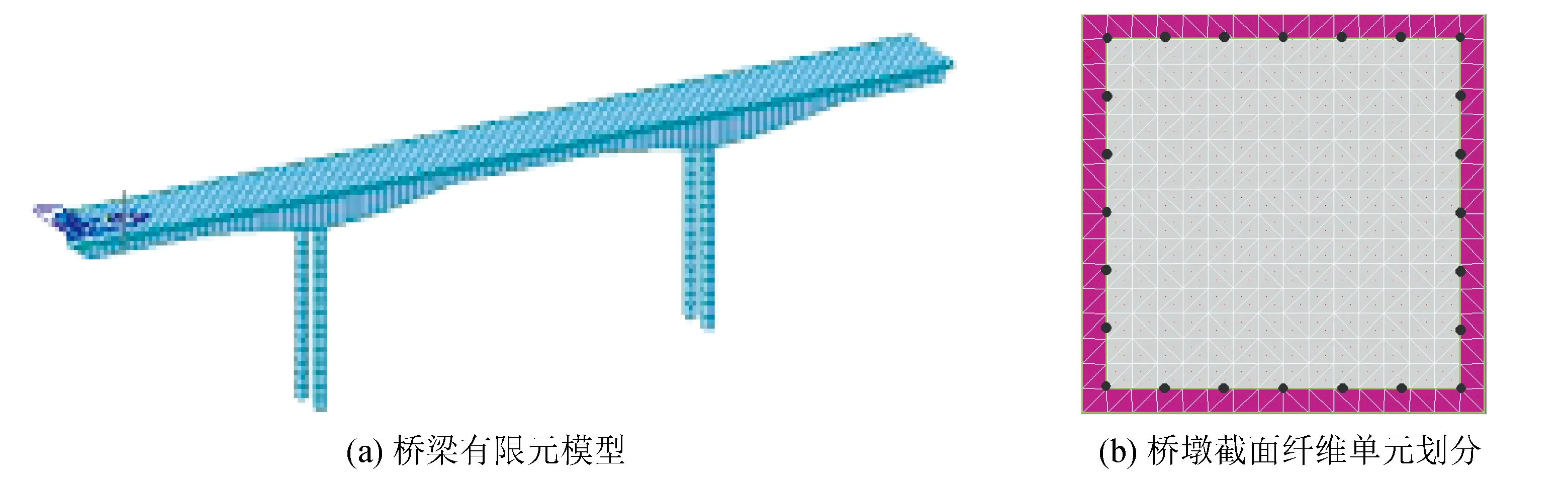
图2 桥梁有限元模型及桥墩截面纤维单元划分Fig.2 Bridge fiite element model and mesh of fiber elements at pier cross-section

为了更好模拟该桥在地震作用下的弹塑性响应,混凝土本构采用Kent-Park混凝土本构[20],包括线性上升段(弹性)、曲线上升段(非弹性)、斜线下降段和平台段。主要参数包含箍筋对混凝土强度提高系数K,混凝土轴心抗压强度fc。桥墩选用OpenSees材料库中的Concrete02本构,考虑混凝土的抗拉性能,将混凝土峰值压应变定义为0.002,极限压应变为0.003 3。

隔震是为了将桥梁结构与可能引起破坏的地面运动尽可能分离开来,一般可通过延长结构的基本周期来实现。为对比分析采用隔震与非隔震支座时该连续梁桥的地震易损性,算例中非隔震情况采用非隔震型盆式支座,主要是依靠支座的允许位移来承担地震力,在地震作用下会发生剪切破坏,且破坏后不具有自动恢复能力。而隔震支座采用铅芯橡胶支座,铅芯塑性变形能吸收地震作用产生的能量,而橡胶能提供较好的水平恢复力,同时由于铅芯的屈服,造成支座的刚度降低,从而改变结构的基本周期。每个桥墩均布置1个支座,4个桥墩布置形式分为2个单向活动支座、1个双向活动支座和1个固定支座。在OpenSees中采用零长度单元模拟支座,单元两个节点的坐标相同,允许在空间6个自由度方向定义线性或非线性的力-位移关系。此外,由于算例关注的是支座隔震效果,为简化分析,采用了墩底固结方式,同时对梁桥两端进行简支处理,不考虑桥台的碰撞效应。

铅芯橡胶支座是最早用于隔震结构的支座之一,凭借其优良的力学性能、较为简单的构造和高性价比,已在实际工程中得到广泛应用。铅芯橡胶支座恢复力模型可以看作双线性模型[21],如图3(a)所示,通过弹性刚度K1、屈服后刚度K2以及屈服强度Qy来表示支座的力学性能。同时Ss为支座的屈服位移,SMax为支座的极限位移,QMax为支座的水平极限承载力。对于本文采用的盆式支座,根据《公路桥梁抗震设计细则(JTG/T B02—01—2008)》[15]建议,其恢复力模型如图3(b)所示,采用双线性理想弹塑性单元模拟。其中K为支座的初始刚度,FMax为活动盆式支座的临界滑动摩擦力,Xy为活动盆式支座的屈服位移。具体建模参数上,铅芯橡胶支座屈服剪力130.85 kN,屈服刚度26 594.51 kN/m,屈服后刚度3 989.17 kN/m。该盆式支座屈服力112.33 kN,屈服刚度22 466 kN/m。根据细则[15],滑动摩擦系数取为0.02,屈服位移取为0.005 m,抗剪能力800 kN。要说明的是,从对桥梁结构动力特性的影响来看,采用盆式支座的桥梁自振周期要低于采用铅芯橡胶支座时的自振周期,因此可以认为该盆式支座属于非隔震类型。

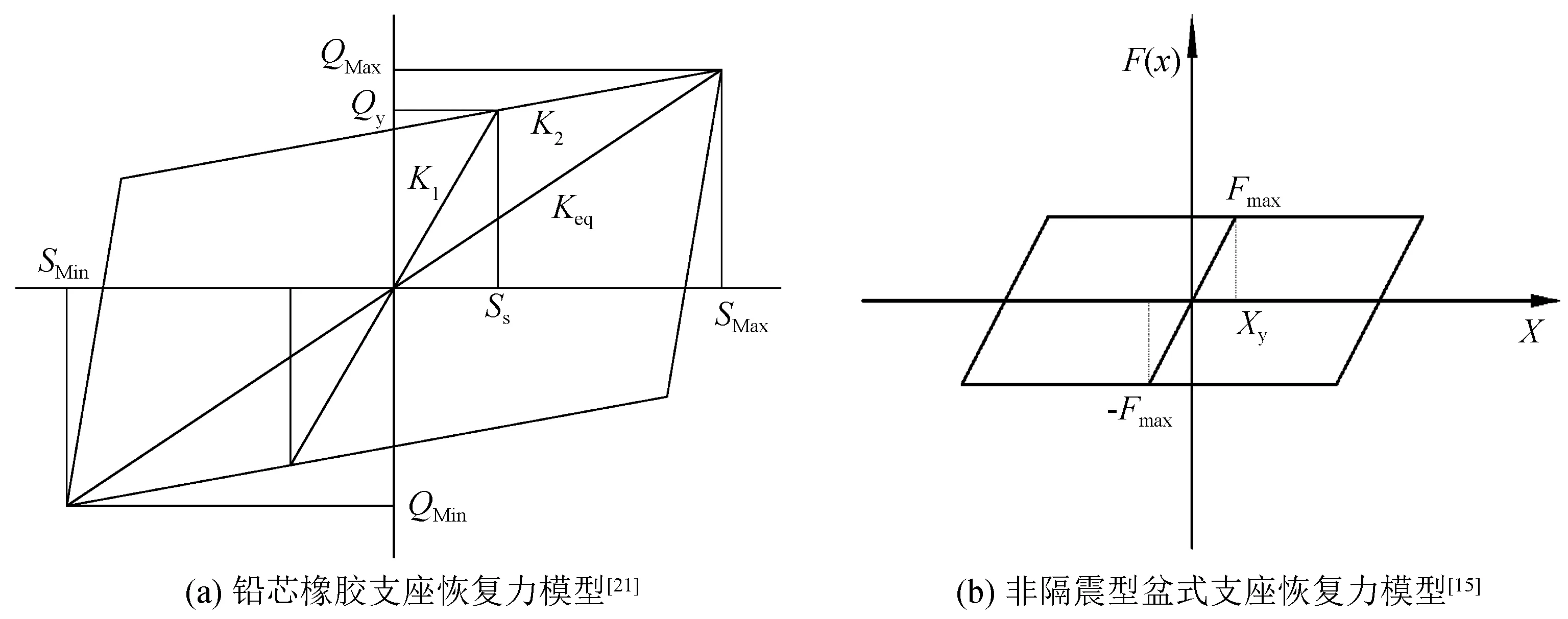
图3 铅芯橡胶支座和非隔震型盆式支座恢复力模型Fig.3 Restoring force models of lead rubber bearing and non-isolated pot bearing

此外,为说明不同支座对箱梁桥动力特性的影响,分析了前3阶自振周期,分别对应一阶纵飘、二阶对称横弯和三阶对称竖弯振型。采用铅芯橡胶支座时周期为3.746 s、0.435 s和0.373 s,采用非隔震型盆式支座时周期为2.169 s、0.321 s和0.208 s,两种支座的周期比值为1.73、1.36、1.79,说明采用铅芯橡胶支座后有效延长了该桥的周期,起到了一定的隔震作用。

3.2 地震波选取

实际地震波具有强烈的随机性,即使在同一场地条件下,同一地震波的记录可能也不尽相同。为了合理的反应桥梁结构在地震作用下的地震响应,并减少地震波不确定性对结构响应的影响,本算例选取50条符合场地周期的、PGA范围为0.034～0.97g的地震波,包含多遇地震和罕遇地震波。同时分析50条地震波的平均反应谱,并与标准反应谱进行对比(图4),发现平均反应谱和所选场地标准反应谱类型相近,仅在T=0.2～0.5 s区域存在一定区别,说明所选的地震波总体上符合要求。由于本算例箱梁桥为规则桥梁,在地震作用下主要是由纵桥向位移过大所导致的破坏,因此仅考虑了纵向地震作用。

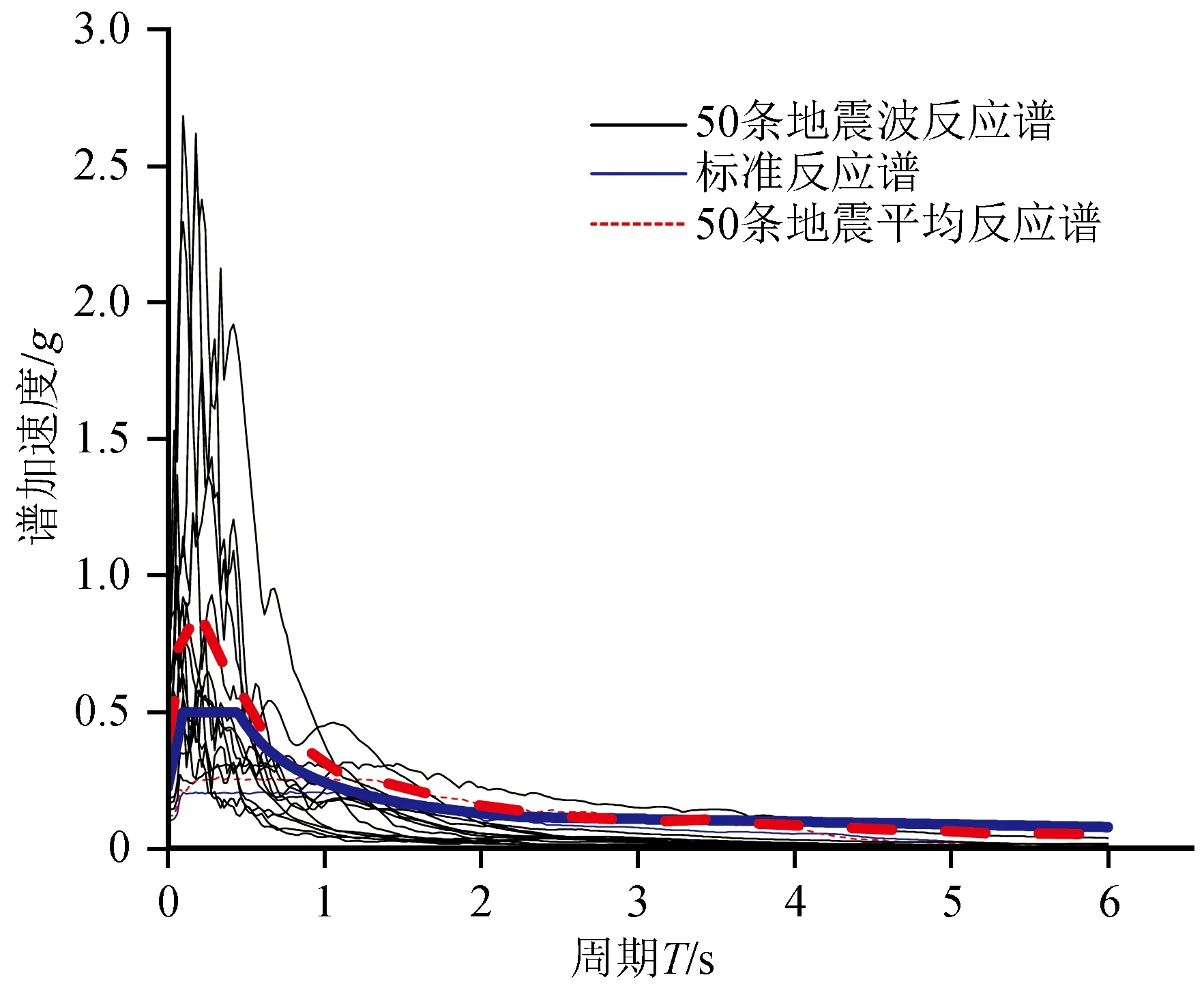
图4 50条地震波反应谱Fig.4 Response spectra of 50 seismic waves

3.3 弯矩-转角分析及支座损伤指标的确定

对桥墩结构进行拟静力分析,求得M-θ骨架曲线,可得屈服转角为0.004 rad,峰值转角0.012 rad,极限转角0.017 rad,失效转角0.021 rad,进一步求得等效屈服转角为0.008 rad,性能点LS的塑性转角为0.014 5 rad。对于铅芯橡胶支座,本文选用的是LRB500型支座,橡胶层总厚度为75 mm,参考2.2节中铅芯橡胶支座破坏状态的定义,计算得到的损伤指标见表2。对于非隔震型普通盆式支座,参考2.2节中的损伤指标的量化,得到的损伤指标亦列于表2。

表2 桥梁构件损伤指标Table 2 Damage indexes of bridge members

3.4 概率地震需求模型

采用选取的50条地震波作为输入,分别对隔震与非隔震支座下连续箱梁桥进行非线性分析,求得桥墩墩顶和支座的最大位移,再对求得数据进行回归拟合(图5、图6)。拟合公式汇总于表3。

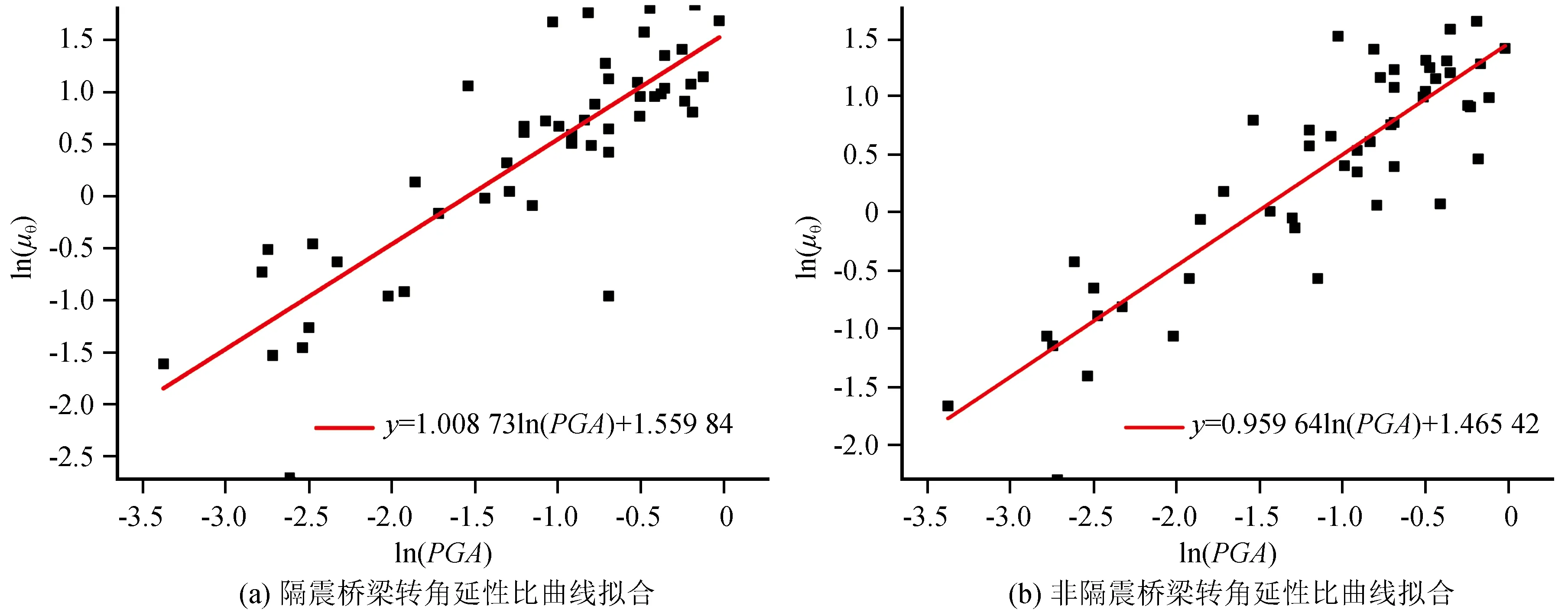
图5 隔震与非隔震桥梁转角延性比曲线拟合Fig.5 Curve fitting of ductility ratio of rotation angle for isolation and non-isolation bridges

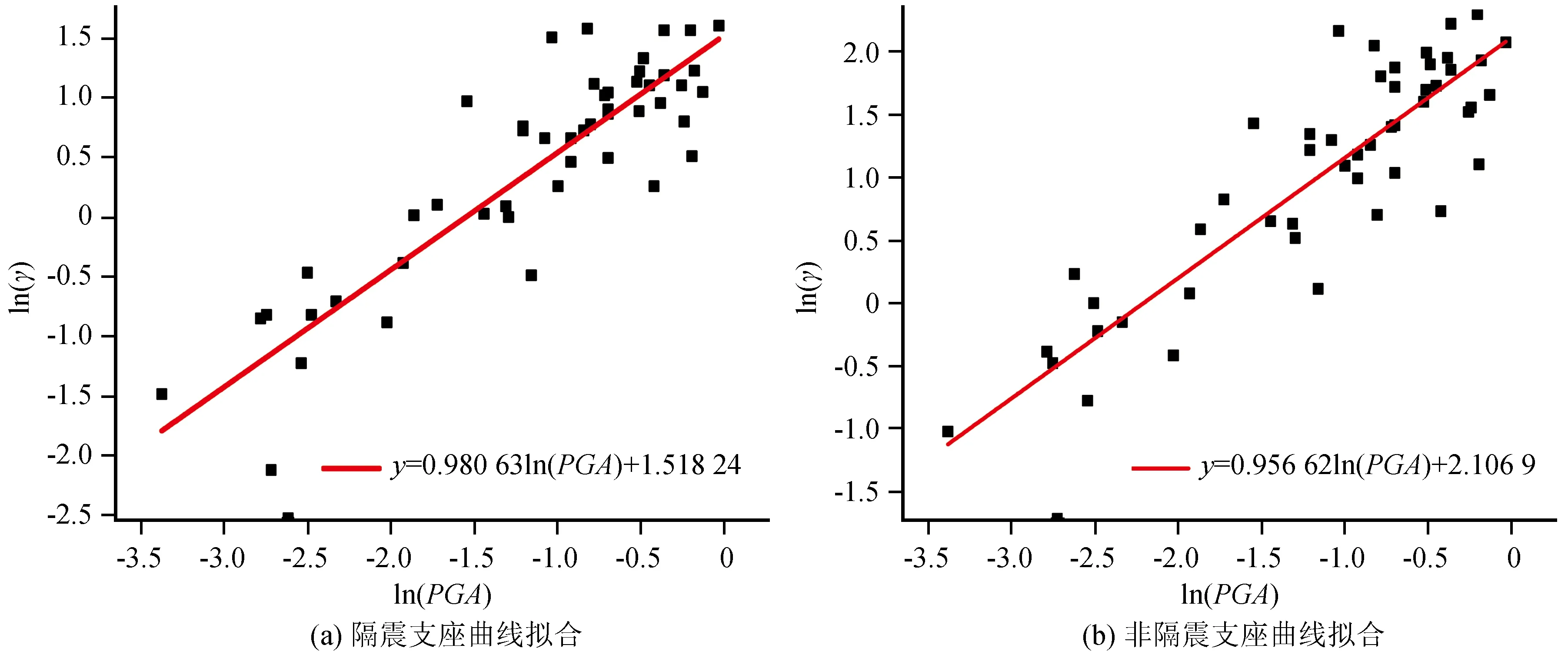
图6 隔震与非隔震支座曲线拟合Fig.6 Curve fitting of isolation and non-isolation bearings

3.5 桥墩和支座易损性曲线

根据式(3)及表3中的数据,可分别求得隔震与非隔震状态下连续箱梁桥桥墩和支座的易损性曲线,如图7所示。由图可见,无论是隔震还是非隔震桥梁,支座易损性曲线的超越概率都大于桥墩,说明支座比桥墩更容易发生破坏。同时采用隔震支座后箱梁桥的桥墩和支座破坏概率都小于非隔震情况。在完全破坏状态下,隔震支座发生破坏的概率为78%,普通支座破坏概率达到97%,差异较大。隔震与非隔震桥墩破坏概率也相差20%左右,说明隔震支座对桥墩起到一定的减震效果。

表3 曲线拟合函数Table 3 Curve fitting function

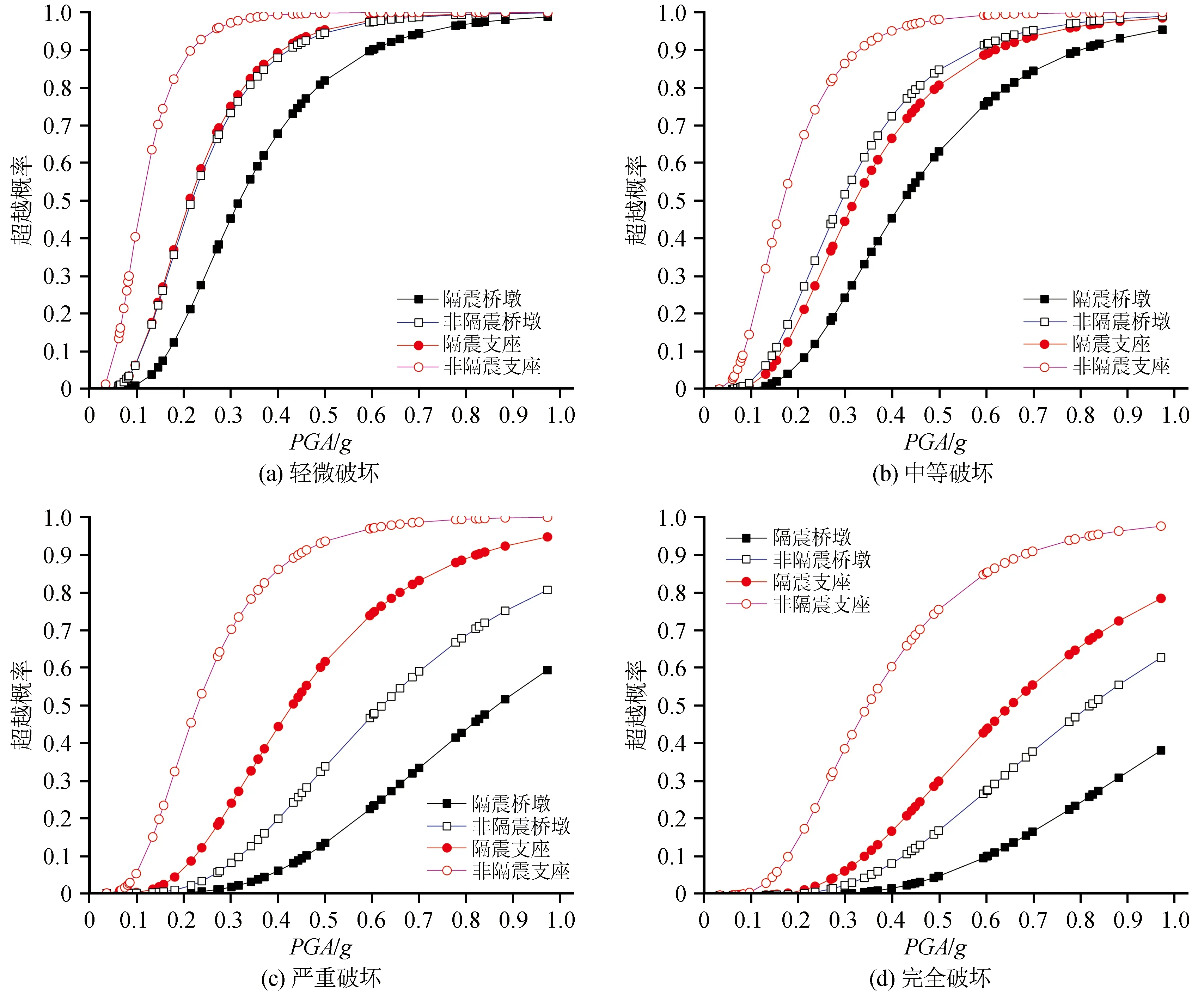
图7 隔震与非隔震桥梁易损性曲线对比Fig.7 Comparison of fragility curves of isolation and non-isolation bridges

3.6 桥梁系统易损性曲线

本文基于式(4)分别计算隔震与非隔震状态下连续箱梁桥的全桥系统地震易损性曲线,如图8所示。同时全桥地震易损性曲线上、下界对比如图9所示。

由图8可见,采用隔震支座后的全桥地震易损性曲线明显小于非隔震情况,且后者地震易损性曲线的上下界宽度比较小,几乎是很相近的。究其原因,首先假设系统上界之间的各构件是互不相关的,从图7可见非隔震桥墩和支座的破坏概率相差很大,且支座最大,故支座在计算全桥地震易损性曲线时所占比重大于桥墩,计算得到的易损性曲线上下界之间相差不大。同理,由于隔震桥墩和支座易损性曲线相差要比非隔震中的要小,故隔震时全桥易损性曲线上下界之间的宽度会比非隔震的宽度要大。由图9可知,无论是系统地震易损性上界还是下界,隔震后全桥的超越概率都小于非隔震时的超越概率,说明采用隔震措施后能较好地降低该连续箱梁桥发生倒塌的概率。

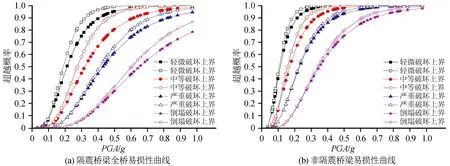
图8 全桥易损性曲线Fig.8 Fragility curves of the whole bridge system

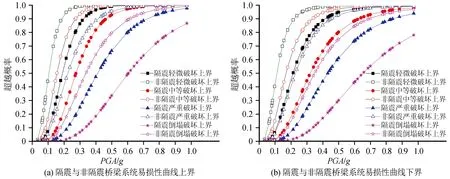
图9 隔震桥梁与非隔震桥梁系统地震易损性曲线对比Fig.9 Comparison between seismic fragility curves of isolation and non-isolation bridges

4 结论

为了分析隔震与普通支座对桥梁地震易损性的影响,本文分别建立了某混凝土连续箱梁桥采用隔震与普通支座时的数值模型,并输入50条实测地震波进行非线性分析,然后提出以转角延性比和支座剪应变作为桥墩和支座的损伤指标,构建了桥墩和支座的地震易损性曲线,再通过一阶界限法计算得到全桥的地震易损性曲线,最后分析对比不同破坏状态下超越概率的上下界,主要得到以下结论:

(1)桥墩“转角延性比”损伤指标同时考虑了桥墩的力和变形两个方面,可以用于对规则梁式桥一般桥墩的地震易损性评价。

(2)通过隔震与非隔震梁桥地震易损性曲线对比发现,各种破坏状态下当PGA相同时,非隔震情况下桥墩和支座的破坏概率都要比隔震时更大。PGA达到1.0g时铅芯橡胶支座发生完全破坏的概率为78%,而非隔震型盆式支座的失效概率达到97%。当PGA较大时,铅芯橡胶支座由于铅芯的屈服能够消耗地震作用能量,从而有效降低支座发生破坏的失效概率。总体上非隔震支座失效概率都比桥墩大,即地震时比桥墩更易损坏。

(3)由于隔震支座延长了梁桥的自振周期,PGA达到0.4g时桥墩才可能发生完全破坏。而采用非隔震型盆式支座时桥墩在0.23g时就有可能发生完全破坏,可见铅芯橡胶隔震支座可以有效减小桥墩在地震作用下的位移,从而降低桥墩的破坏概率。

(4)通过全桥地震易损性分析发现,梁桥系统比单一构件如桥墩和支座更容易破坏。非隔震梁桥的系统易损性上下界宽要小于隔震梁桥的上下界宽。采用铅芯橡胶隔震支座能够有效降低梁桥发生各种破坏的概率。