一种新型结构的盆式绝缘子力学性能研究
2022-12-27鲁少阳1b刘展程
鲁少阳,王 爽,1b,刘展程,张 勤
(1.三峡大学a.电气与新能源学院;b.湖北省输电线路工程技术研究中心,湖北 宜昌 443002;2.国网乐山供电公司,四川 乐山 614000)
0 引言
盆式绝缘子是气体绝缘开关(GIS)和气体绝缘金属封闭输电线路(GIL)的重要组成部分[1-3]。盆式绝缘子通常工作在充满SF6气体的环境中,往往需要承受气体产生的压强且起着支撑及隔绝气室的作用,因此盆式绝缘子要有足够的机械强度[4-8]。
对于盆式绝缘子力学性能的研究主要是基于有限元仿真和试验测试展开的。文献[9]研究了三相交流盆式绝缘子表面的应力分布,将盆式绝缘子表面应力集中由“Y”型分布转化为“△”型分布,降低了其最大应力值。文献[10-12]通过水压试验和仿真研究了1 100 kV GIS盆式绝缘子的力学性能,加强了其中心嵌件与盆式绝缘子接触后的机械强度。文献[13]通过建立三维应力仿真模型,并配合水压破坏试验,得到盆式绝缘子在不同负载下的设计裕度。文献[14]利用有限元仿真模型改变局部参数来研究盆式绝缘子的力学性能。文献[15-17]通过有限元仿真和水压试验研究了盆式绝缘子表面的应力分布,但其水压试验相对简单。目前对于盆式绝缘子力学性能的研究往往局限于交流工况且仿真计算模型比较简单,大多未考虑橡胶密封圈对计算结果的影响,因此缺乏工程实际意义且准确性较低。
本文主要研究一种新型结构的直流GIS盆式绝缘子的力学性能,该盆式绝缘子采用盘式结构,能有效降低电场强度。通过有限元仿真和水压试验,计算不同压力下盆式绝缘子的应变和应力,对结果进行分析,得到该直流盆式绝缘子的表面应力分布,为直流盆式绝缘子的结构优化和设计提供思路。
1 盆式绝缘子力学性能仿真计算
1.1 盆式绝缘子模型的构建
本文研究的直流盆式绝缘子模型如图1所示。该盆式绝缘子模型是一种盘状结构的绝缘子,没有凹面与凸面之分,在直流电压下电场分布较均匀。模型整体为轴对称结构,中心为导体嵌件,外圈装配法兰,嵌件和法兰为铝合金材料,盆式绝缘子为环氧树脂/氧化铝复合材料。
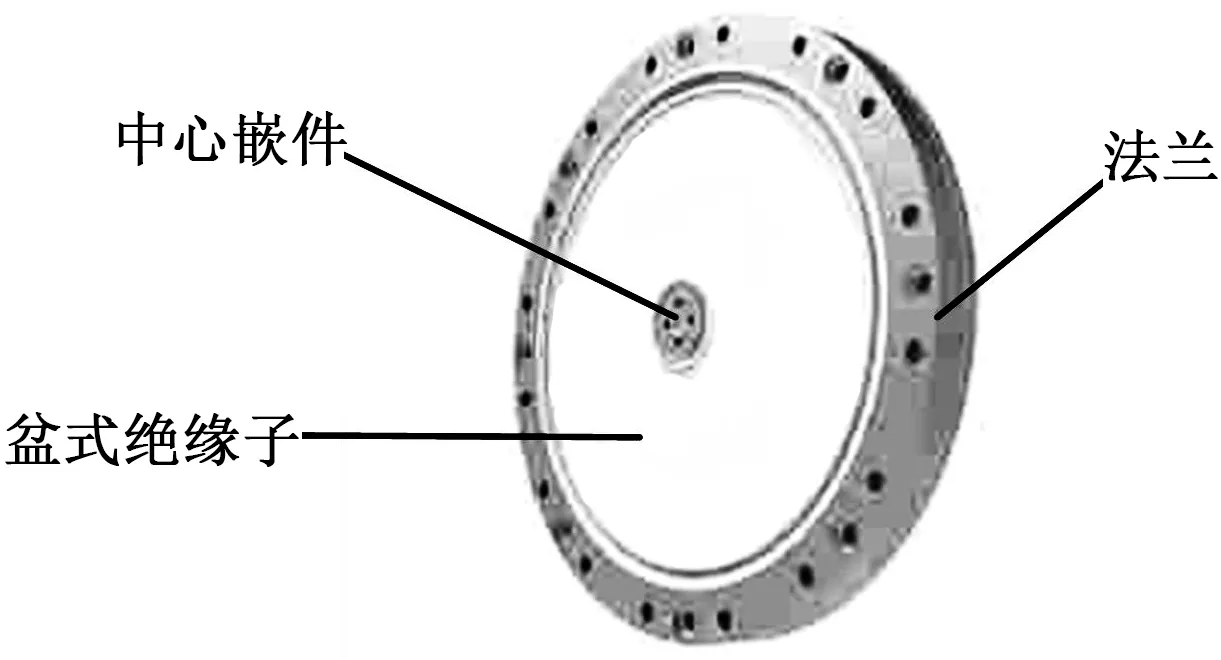
图1 盆式绝缘子示意图Fig.1 Diagram of basin insulator
在仿真和水压试验研究中,对盆式绝缘子进行建模,各组装、工装零部件(水压盖板、水压支撑筒、紧固螺栓等)的材料属性设置见表1。

表1 材料属性设置Tab.1 Material attribute settings
1.2 盆式绝缘子机械应力分布计算
橡胶密封圈是保障盆式绝缘子气密性的关键部件,为了研究橡胶密封圈对盆式绝缘子应力分布的影响,在压力作用下分别对加有橡胶密封圈和不加橡胶密封圈的盆式绝缘子应力分布进行对比分析。
为了在保证计算精度的同时,提高计算效率,本研究对盆式绝缘子模型进行一定的简化,忽略螺栓及螺栓连接孔等元素。
由于盆式绝缘子为轴对称结构,在仿真时使用二维轴对称模型进行应力分析。此外,本研究的盆式绝缘子并无凹面与凸面之分,任选一面施加水压即可。
该盆式绝缘子的额定压力值为0.6 MPa,设计压力值为0.8 MPa。按照国家电网企业标准水压破坏值应不小于3倍的设计压力[18],即2.4 MPa。本研究在仿真计算中分别计算了2.0、2.1、2.2、2.3、2.4 MPa水压下盆式绝缘子的应力和应变结果。限于篇幅,本研究主要介绍盆式绝缘子在2.4 MPa水压下的应力分布情况。
1.2.1 未加橡胶圈的盆式绝缘子仿真分析
未加橡胶圈的盆式绝缘子仿真模型主要由中心嵌件、盆式绝缘子、屏蔽环、法兰、压力盖板组成,如图2所示。

图2 未加橡胶圈的盆式绝缘子结构图Fig.2 Structure diagram of basin insulator without rubber ring
无橡胶圈的盆式绝缘子在2.4 MPa水压下的应力分布仿真结果如图3所示。由图3可知,在没有橡胶圈时盆式绝缘子所受最大应力为85.76 MPa,大于材料的抗拉强度(78.50 MPa),超出幅度为9.25%。最大应力出现在盆式绝缘子装配橡胶圈的凹槽内。

图3 未加橡胶圈的盆式绝缘子2.4 MPa下的应力分布Fig.3 Stress distribution of basin insulator without rubber ring under 2.4 MPa pressure
1.2.2 加橡胶圈的盆式绝缘子仿真分析
加橡胶圈的盆式绝缘子仿真模型主要由中心嵌件、盆式绝缘子、屏蔽环、法兰、橡胶圈、压力盖板组成,如图4所示。

图4 加橡胶圈的盆式绝缘子结构图Fig.4 Structure diagram of basin insulator with rubber ring
橡胶材料具有超弹特性,本研究采用Mooney-Rivlin模型来描述橡胶圈的本构关系[19],其方程如式(1)所示。

式(1)中:C01、C10为穆尼常数,其中C01=0.036 4 MPa,C10=0.728 MPa;D1为不可压缩比,D1=0.01;I1、I2为Green应力张量的两个主不变量。
加橡胶圈的盆式绝缘子在2.4 MPa水压下的应力分布仿真结果如图5所示。由图5可知,加橡胶圈的盆式绝缘子在水压为2.4 MPa时所受的最大应力为88.69 MPa,大于材料的抗拉强度(78.5 MPa),超出幅度为12.98%。盆式绝缘子应力最大值位于其表面凹槽处,距离中心嵌件155 mm。产生应力集中的区域位于距离中心嵌件100~200 mm处(见图5中盆式绝缘子下端红色区域)。

图5 加橡胶圈的盆式绝缘子2.4MPa下的应力分布Fig.5 Stress distribution of basin insulator with rubber ring under 2.4 MPa pressure
在加橡胶圈的盆式绝缘子仿真计算中,水压为2.0、2.1、2.2、2.3 MPa时盆式绝缘子产生应力集中的区域与水压为2.4 MPa时的结果相一致,应力最大值随着水压的升高而增大。
2 盆式绝缘子水压试验装置与测量系统
2.1 水压试验装置
水压试验装置结构如图6所示,由加压管、接头、水压盖板、橡胶圈、紧固螺栓、水压支撑筒等组成。水压试验装配时盆式绝缘子密封槽外台与筒体法兰的间隙为0.3 mm,以保证只有密封槽和盆式绝缘子法兰受力。
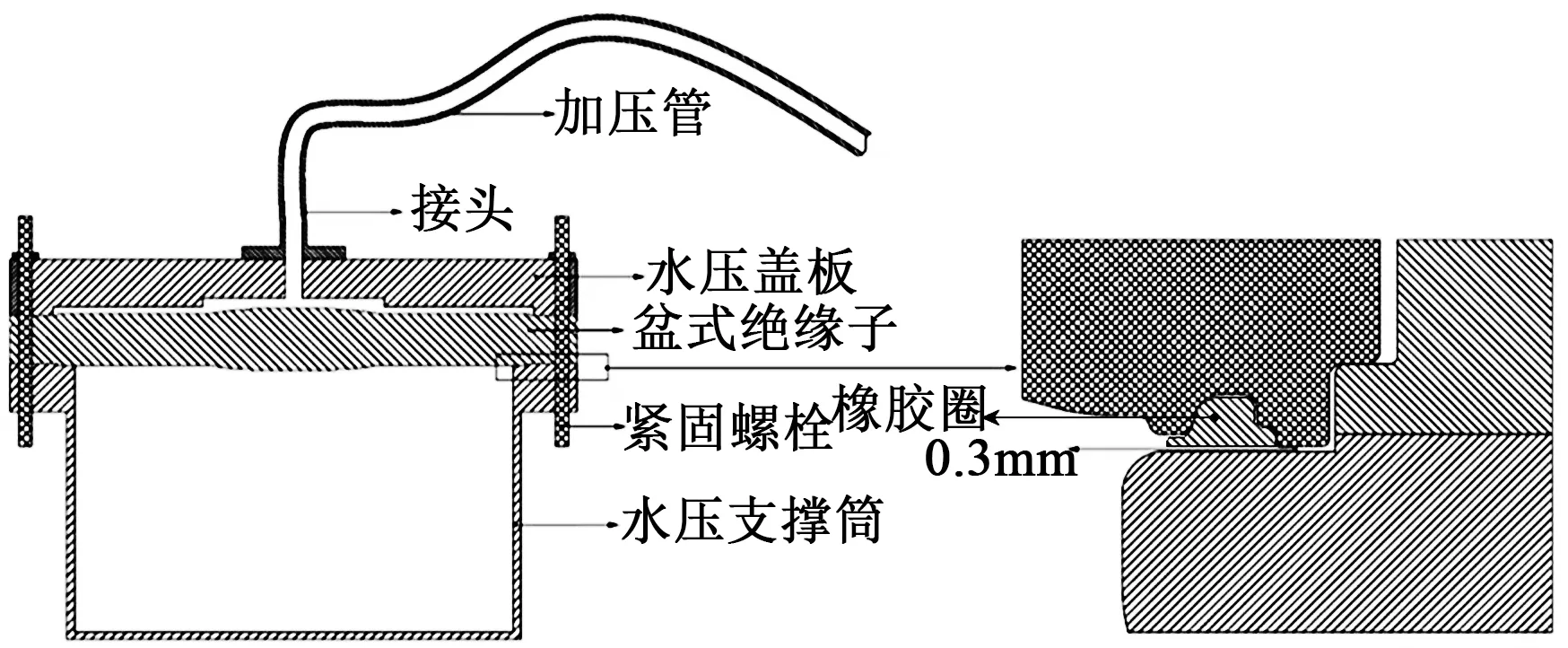
图6 水压试验装置结构图Fig.6 Structure diagram of hydrostatic test device
2.2 测量系统
2.2.1 测量装置介绍
本研究在盆式绝缘子表面粘贴BHF350-3AA(XX)型电阻应变片,从而在水压试验过程中得到绝缘子表面应变值。试验采用JC-4B型电阻应变仪,选择9通道测试模式,补偿片固定于环氧复合件。
电阻应变片是在非电量电测技术领域中应用最广泛的传感元件之一,其工作原理是基于金属电阻丝的电阻应变效应,当金属电阻丝在轴向受到拉伸时,其电阻增大,而受到压缩时,其电阻减小。该应变片多用于金属和复合材料应力应变的测量。应变片自带2米长的绝缘导线,可有效避免部分短路情况,方便应变片的固定。由于盆式绝缘子所用复合材料为各向同性材料,在理想状态下,可假设各个方向的收缩应变值一致,测试所用应变片为双向应变片。根据应变片测得的应变值,可计算相应应力值。
2.2.2 测量试验
在绝缘子表面粘贴20片应变片,具体位置见图7。1~7、8~14号测点沿着绝缘子表面一字排开,在水平面呈90°,各个应变片与中心嵌件的距离如图7(a)所示,对绝缘子表面应变进行全面系统的测量;15~17、18~20号测点重点对绝缘子距离中心嵌件67、105、132 mm处进行测量。完成水压试验装置装配后,以平均不超过400 kPa/min的速度上升至盆式隔板的两倍设计压力,保压10 min,继续升压至2.1 MPa时盆式绝缘子试品发生破坏。试验对绝缘子进行0.6、0.7、0.8、0.9、1.0、1.1、1.2、1.3、1.4、1.5、1.6、1.7、1.8、1.9、2.0、2.1 MPa等16个水压等级的应变数据采集。
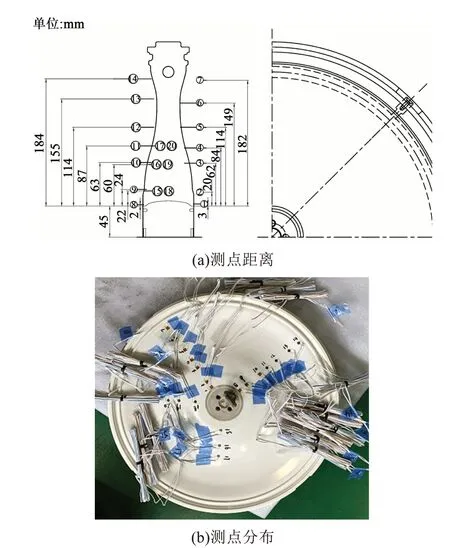
图7 绝缘子表面测点分布Fig.7 Distribution of measuring points on insulator surface
3 水压试验数据分析
根据图7中对测量点应变片的布置,本次试验使用直角双向应变片,可同时测量得到测点位置的周向应变值和径向应变值。
3.1 周向应变
1~7、8~14号测点的周向应变分别如图8、图9所示。由图8~9可知,绝缘子的周向应变随着水压的升高,呈线性增大,离中心嵌件越远,周向应变越大。

图8 测点1~7周向应变值Fig.8 Circumferential strain value of measuring points 1-7

图9 测点8~14周向应变值Fig.9 Circumferential strain value of measuring points 8-14
15~17、18~20号测点的周向应变分别如图10、图11所示。由图10~11可知,15~17、18~20号测点周向应变随水压的升高而变大,离中心嵌件越远,周向应变越大。
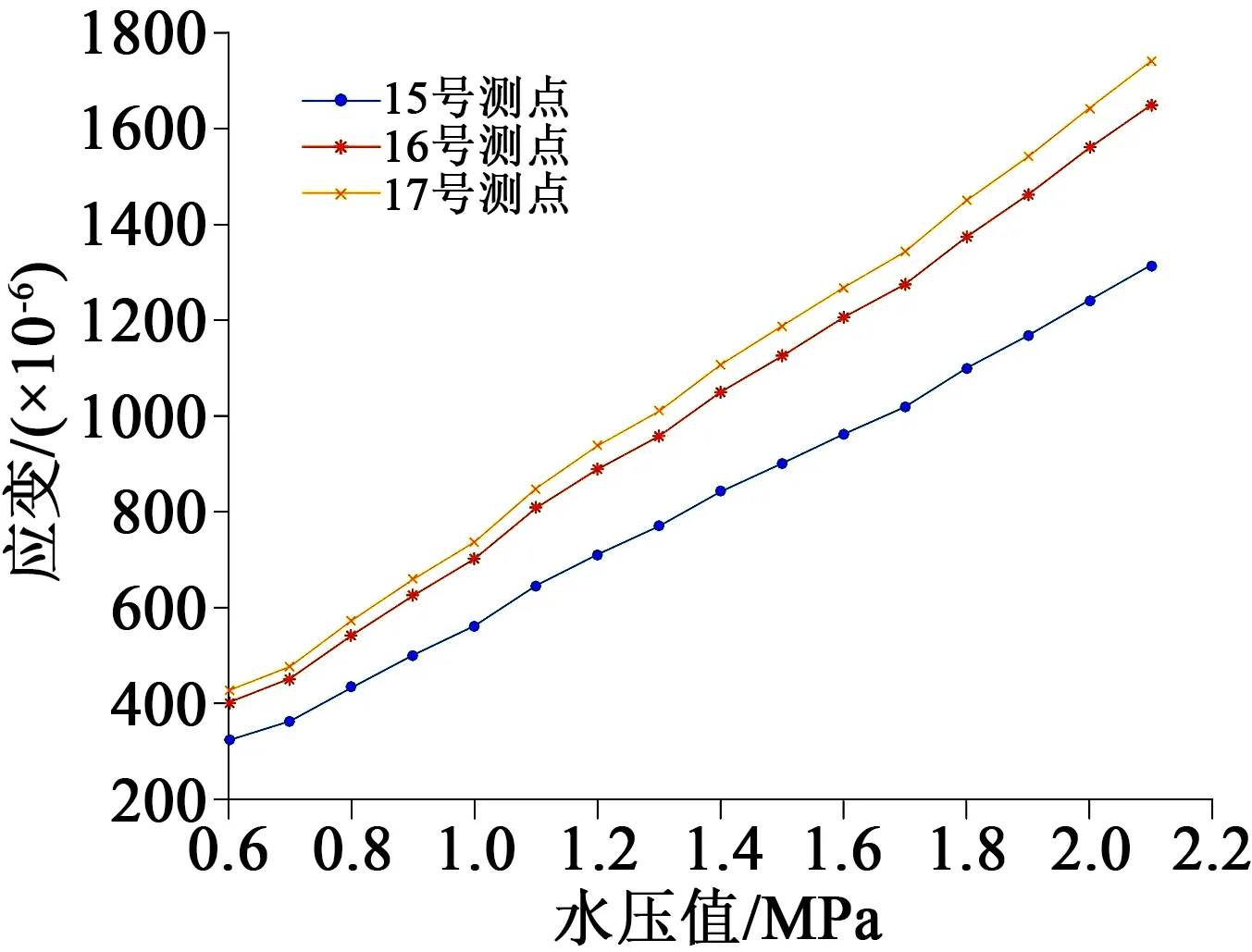
图10 测点15~17周向应变值Fig.10 Circumferential strain value of measuring points 15-17

图11 测点18~20周向应变值Fig.11 Circumferential strain value of measuring points 18-20
3.2 径向应变
1~7、8~14号测点的径向应变分别如图12、图13所示。由图12~13可知,1~5、8~12号测点的径向应变值随着水压的升高而变大,离中心嵌件距离越远,应变越大。6、7和13、14号测点的径向应变值随着水压的升高而变大,但离中心嵌件距离越远应变越小,其中7、14号测点的径向应变值为负值,说明盆式绝缘子的该位置被压缩。1~7号测点中5号测点的径向应变值最大,8~14号测点中12号测点的径向应变值最大。5、12号测点与中心嵌件的距离均为159 mm,其中5号测点的径向应变值大于12号测点的径向应变值。在2.0 MPa工况下5号测点的实际测量应变值为6 307×10-6,在加橡胶圈时的仿真计算结果中提取的应变值为6 686×10-6,误差为6.0%;在2.1 MPa工况下5号测点的实际测量应变值为6 750×10-6,在加橡胶圈时的仿真计算结果中提取的应变值为6 979×10-6,误差仅为3.4%,如表2所示,其中水压在2.1 MPa时盆式绝缘子试品已发生破裂,因此未采集水压为2.2、2.3、2.4 MPa下的试验数据。将水压为2.0、2.1 MPa下的应变计算值和试验测量值进行对比,说明了仿真计算结果的准确性。

表2 不同压力下径向应变值对比Tab.2 Comparison of radial strain values under different pressures
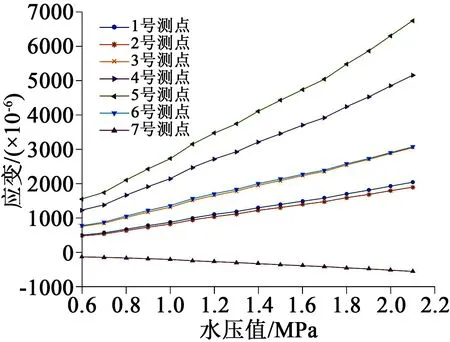
图12 测点1~7径向应变值Fig.12 Radial strain value of measuring points 1-7

图13 测点8~14径向应变值Fig.13 Radial strain value of measuring points 8-14
15~17、18~20号测点的径向应变分别如图14、图15所示。由图14~15可知,15~17、18~20号测点的径向应变随水压的升高而变大,距中心嵌件越远,应变越大。

图14 测点15~17径向应变值Fig.14 Radial strain value of measuring points 15-17

图15 测点18~20径向应变值Fig.15 Radial strain value of measuring points 18-20
对比15~17、18~20号测点测得的周向应变值和径向应变值,其数值差别不大,说明盆式绝缘子圆周面上直径相同位置的应变是大致相同的。比较各个测点的周向和径向应值变可知,盆式绝缘子受压后径向应变大于周向应变。
3.3 水压试验数据分析
根据虎克定律,可应用式(2)~(3)[20-21]将应变换算成主应力。

式(2)~(3)中:εθ、εr是测点的周向、径向应变;σθ、σr是周向和径向的主应力;E、v是弹性模量和泊松比。
每一个测点的应力状态可以用σ1、σ2、σ3三个主应力描述,分别指第一、二、三主应力,以1号测点为例,根据式(2)、(3)得到周向应力与径向应力见图16。由材料第四强度理论,将绝缘子所受主应力由大到小依次排列为σ1、σ2、σ3(其中σ3取值为0)。由图16可知,不同水压下径向应力均大于周向应力,因此有σ1=σr、σ2=σθ。换算成米塞斯应力,如式(4)所示。

图16 测点1径向应力与周向应力值Fig.16 Radial and circumferential stress values of point 1

由式(4)计算得到不同水压下各个测点的等效应力值如图17~20所示。

图17 测点1~7等效应力值Fig.17 Equivalent stress value of measuring points 1-7

图18 测点8~14等效应力值Fig.18 Equivalent stress value of measuring points 8-14
由图17~18可知,1~5、8~12号测点的等效应力值随着水压的升高而变大,离中心嵌件距离越远等效应力值越大,6、7和13、14号测点的等效应力值随着水压的升高而变大,但离中心嵌件距离越远,等效应力值越小。5、12号测点在2.1 MPa工况下的等效应力值分别是81.52 MPa、79.34 MPa,分别超出材料测试抗拉强度的3.8%和1.07%。
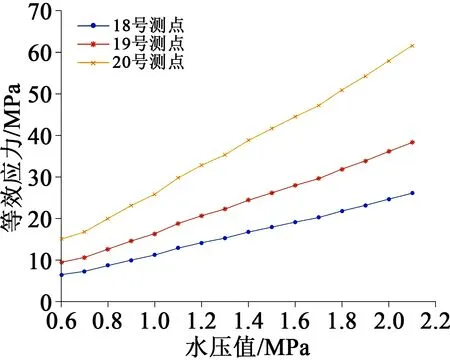
图20 测点18~20等效应力值Fig.20 Equivalent stress value of measuring points 18-20
测点1、2、7随水压升高应力增大较为平缓。测点3、4、5、6随水压升高应力增幅较大,其中测点3、4、5、6距中心嵌件107~194 mm。测点8~14中10、11、12、13号测点随水压升高应力增幅较大,这些测点距中心嵌件108~200 mm。可以看出绝缘子表面应力随着压力的升高而增大,但产生应力集中的位置保持不变,位于距离中心嵌件107~200 mm处。
在仿真中加橡胶圈的盆式绝缘子受压后产生应力集中的区域与水压试验得出的应变值换算成应力值所分析的盆式绝缘子产生应力集中的区域相一致,位于盆式绝缘子表面凹槽,距离中心嵌件107~200 mm处。而未加橡胶圈的盆式绝缘子仿真得到的应力集中区域在装配橡胶圈的凹槽部位,且应力值也较小,与盆式绝缘子实际工况中装配橡胶圈的水压试验结果不符。
由图19~20可知,15~17、18~20号测点等效应力值随水压升高而变大,离中心嵌件距离越远,等效应力值越大。

图19 测点15~17等效应力值Fig.19 Equivalent stress value of measuring points 15-17
对比15~17、18~20号测点的等效应力值,其数值差别不大,说明盆式绝缘子圆周面上直径相同位置的应力值是大致相同的。
3.4 水压试验结果分析
通过仿真计算分析,在2.4 MPa的压力下,盆式绝缘子最易破损的中部最大应力值为88.69 MPa,裕度为0.885(抗拉强度/最大应力=78.5/88.69=0.885),表明该盆式绝缘子的机械强度不可靠,其力学性不能满足设计要求,不可以用于产品。
在水压试验中,当水压值达到2.1 MPa时,盆式绝缘子会发生破坏,两个绝缘子的破坏情况如图21所示。试验结束后,用红色水笔描出盆式绝缘子试品的裂缝,可以看到裂纹在水平面呈一定的对称分布,盆式绝缘子破坏起始位置为9号测点附近距中心嵌件110~120 mm处。破坏裂纹呈树枝状从里向外延伸。

图21 水压试验后盆式绝缘子破坏情况Fig.21 Damage condition of basin insulator after hydrostatic test
4 结论
(1)在2.0 MPa、2.1 MPa两种工况下的实际测量应变值与加橡胶圈仿真中得到的应变值误差分别为6.0%和3.4%,说明加橡胶圈的仿真结果符合工程实际情况,仿真结果可靠。
(2)通过仿真和水压试验数据分析找出了盆式绝缘子发生应力集中的位置位于距离中心嵌件107~200 mm处,得到盆式绝缘子发生破裂的起始位置距离中心嵌件110~120 mm处。
(3)随着水压的升高,同一测点的应变值、应力值呈线性增长;盆式绝缘子同一测点的径向应变大于周向应变;盆式绝缘子圆周面上直径相同的位置应变、应力大致相同。
(4)在水压试验中,当水压值达到2.1 MPa时,盆式绝缘子会发生破坏,其裂纹在水平面上呈一定的对称分布。
(5)该绝缘子为适应直流电场采用盘式结构,虽然能够有效地降低电场强度,但是其力学性能未达到额定要求的标准,即2.4 MPa,因此后续研究中还需对其结构进行优化,以满足标准规定的力学性能要求。
