基于KPCA-GA-ELM 的海底管道外腐蚀速率预测技术
2021-12-06高帅
高 帅
(中海石油(中国) 有限公司深圳分公司, 广东 深圳 518000)
海底油气输送管道作为海上油气田开发生产系统与处理系统的重要连接部分, 是海上油气运输的重要通道。 海水中含有大量腐蚀性较强的天然电解质, 为电化学反应创造了条件,海底管道一旦泄漏, 会造成重大的经济损失和环境污染[1-2]。 目前, 对于海底管道完整性的研究多偏向内腐蚀, 但在复杂多变的海洋环境中,外腐蚀也是造成海底管道失效的原因之一[3]。 因此, 梳理海水腐蚀因素, 建立可靠的外腐蚀速率预测模型对于提高管道完整性管理水平有着重要意义。
目前, 国内外学者针对海底管道腐蚀问题开展了一系列研究。 张新生等[4]在考虑随机效应的前提下, 应用贝叶斯网络对腐蚀深度进行预测; 毕傲睿等[5]采用主成分分析对影响管道腐蚀的土壤因素进行了筛选, 并结合维纳退化过程对管道剩余寿命进行了预测; 王奇等[6]采用BP 神经网络对外腐蚀速率进行了预测; 者娜等[7]采用支持向量机模型对管道腐蚀速率进行了预测。 以上成果对于海底管道腐蚀的研究具有一定意义, 但贝叶斯网络、 BP 神经网络及支持向量机模型结构复杂, 在训练过程中容易陷入局部最优解; 主成分分析主要解决线性问题, 对于海洋环境而言, 海底管道受多种腐蚀因素影响, 主成分分析无法适应非线性、 小样本的数据降维和映射问题。 基于此, 采用核主成分分析(kernel principal components analysis,KPCA) 对影响海底管道腐蚀的因素进行筛选, 并将数据代入极限学习机 (extreme learning machine,ELM) 进行训练[8], 采用遗传算法(genetic algorithm,GA) 对ELM 的输入权值和隐含层偏差进行优化, 建立外腐蚀速率预测模型, 以期为海底管道的安全运行提供理论依据。
1 KPCA 原理
KPCA 在主成分分析基础上引入核函数的概念, 对样本xk(k=1,2,3,…m) 采用非线性函数φ (xk) 进行变换, 将其从低维空间映射到高维空间F, 此时特征空间的协方差矩阵为

式中: a——核矩阵K 的特征向量。
由于径向基函数可将数据映射到无限高维空间, 故选用该函数作为核函数。 经计算, 提取累积方差百分比≥90%的主成分作为影响海底管道外腐蚀速率的主要因素。
2 ELM 算法
ELM 算法[9]由黄广斌教授提出, 用于训练单隐含层的前馈神经网络, 可用于分类、 预测和回归分析。 与BP 神经网络不同, ELM 算法的输入权值和隐含层偏差均随机产生, 输出权值依据广义逆矩阵理论解析求出, 无需误差反向传播训练权值, 具有训练参数少、 学习速度快、 鲁棒性强的特点。
在KPCA 数据降维的基础上, 利用ELM 算法挖掘腐蚀因素与腐蚀速率之间的内在联系, 从而预测腐蚀速率。 模型如下:

式中: yi——样本输出值;
xi——样本输入值;
wij——第i 个输入层节点与第j 个隐含层节点之间的权值, 即输入权值;
bj——隐含层神经元偏差;
βjk——第j 个隐含层节点与第k 个输出层节点之间的权值, 即输出权值;
g (x) ——隐含层激活函数;
m——隐含层节点数, 当给定隐含层的节点数后, 可依据广义逆矩阵理论计算输出权值βjk, 使预测输出值yi的误差最小。
为动态求解ELM 算法中的输入权值和隐含层偏差, 采用GA 算法对其进行优化处理。 GA算法是模拟达尔文的生物进化自然选择和孟德尔的遗传进化过程来搜索最优解, 属于并行、 全局搜索方式, 可在搜索过程中自动累积先验知识,并自适应控制搜索过程以获得全局最优解[10-11]。
为进一步提高遗传算法在不同阶段的进化适应性, 对GA 算法进行改进。 引入反余弦函数改变交叉、 变异因子的计算方法, 在保证种群多样性和稳定性的前提下, 避免出现局部最优解。 改进公式如下:

式中: Pc和Pm——交叉、 变异因子;
Pcmax、 Pcmin——交叉因子的最大值和最小值;
Pmmax和Pmmin——变异因子的最大值和最小值;
Si——当前适应度;
Savg——适应度平均值。
3 基于KPCA-GA-ELM 算法的腐蚀预测模型
本研究提出的基于KPCA-GA-ELM 算法的腐蚀预测模型详细流程如下:
(1) 数据预处理, 构建海底管道外腐蚀评价指标体系, 对数据进行归一化处理。 假设有N个腐蚀样本, 影响因素为m 个, (xi, yi) 为第i 个样本数据, 其中xi= [xi1, xi2, …xim] 作为输入,yi作为输出, 采用极值法进行归一化处理,

式中: x′ie——第i 个样本的第e 个影响因素归一化后的数据;
xie——归一化前的原始数据;
xemax和xemin——样本范围内第e 个影响因素的最大值和最小值。
(2) 将处理后的数据代入KPCA 模型中进行数据优选。
(3) 将步骤 (2) 中数据分为训练集和验证集, 随机抽取前者为44 组, 后者为6 组, 将训练集代入ELM 模型, 以预测值和真实值之间的平均相对变动率(ARV) 作为适应度函数, 通过GA 模型的选择、 交叉和变异, 经多次迭代后不断优化ELM 算法中的输入权值和隐含层偏差,得到最优的GA-ELM 模型。
(4) 将验证集数据代入训练好的GA-ELM模型, 并采用均方误差 (MSE)、 平均相对误差(MAPE) 和相关系数R2评价预测结果, 其中MSE、 MAPE 的数值越小, 模型偏差越小; R2的值越接近1, 预测值与实际值之间的相关性越大, 拟合优度越好。 公式如下,
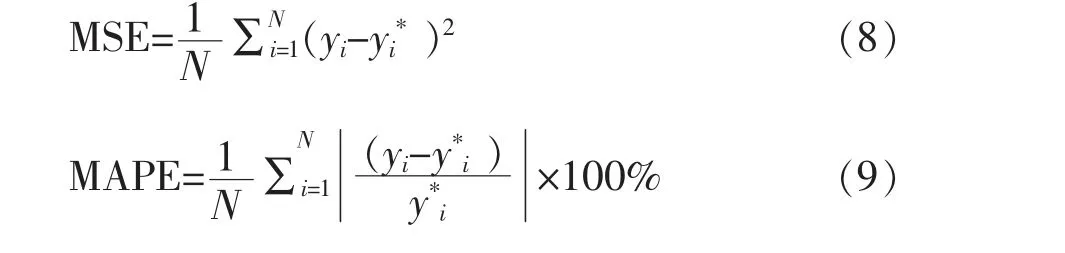
式中: N——腐蚀样本个数;
yi——第i 个样本的腐蚀速率实际值;
y*i——第i 个样本的腐蚀速率预测值。
4 实例验证
海底管道腐蚀主要与海洋环境中的物理、化学和生物因素有关, 其中SRB (硫酸盐还原菌) 和真菌等微生物对管道的腐蚀作用主要体现在细菌的新陈代谢上, 微生物产生硫化物,从而改变海水的氧含量和pH 值, 故不再对微生物进行单独考虑。 基于此, 选择盐度、 温度、 溶解氧、 氧化还原电位、 pH 值、 流速、硫化物和海洋生物附着度等8 个因素作为影响海底管道外腐蚀速率的主要因素。 对某海底管道沿线设置50 组挂片进行实海挂片试验, 挂片尺寸100 mm×100 mm×5 mm, 在200 天后得到管道沿线不同海洋环境下的腐蚀数据, 部分数据见表1。
对表1 中的数据进行归一化处理后代入KPCA 模型, 对数据采用相关性矩阵和规划分析计算特征值和方差百分比, 计算结果见表2 和图1。
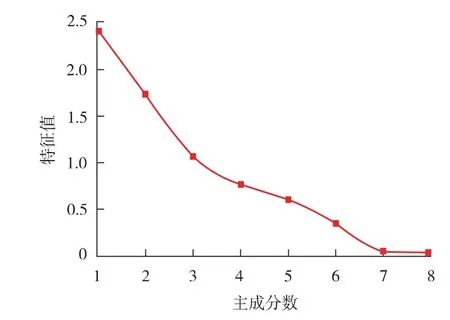
图1 主成分分析碎石图
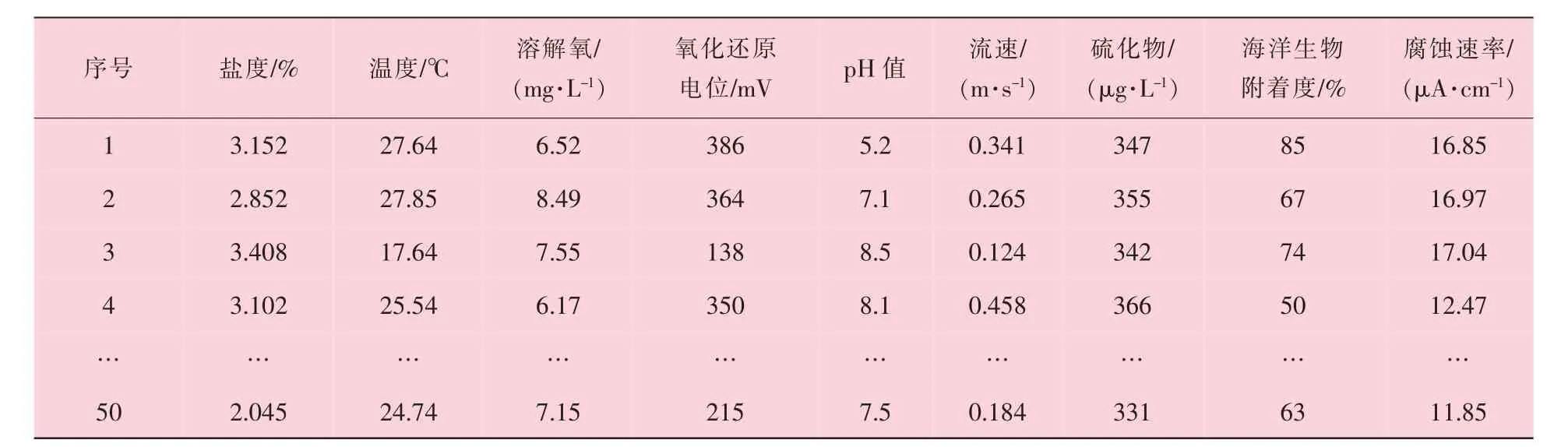
表1 某海底管道沿线腐蚀数据统计结果

表2 KPCA 分析结果
从图1 可知, 前5 个主成分之间的特征值差异较大, 且累积贡献率为94.17%, 超过90%,因此可以选取前5 个主成分代替原先的8 个影响因素, 根据主成分的系数矩阵对数据进行重组,样本数据由之前的8 维变为5 维, 重组后的样本数据见表3。
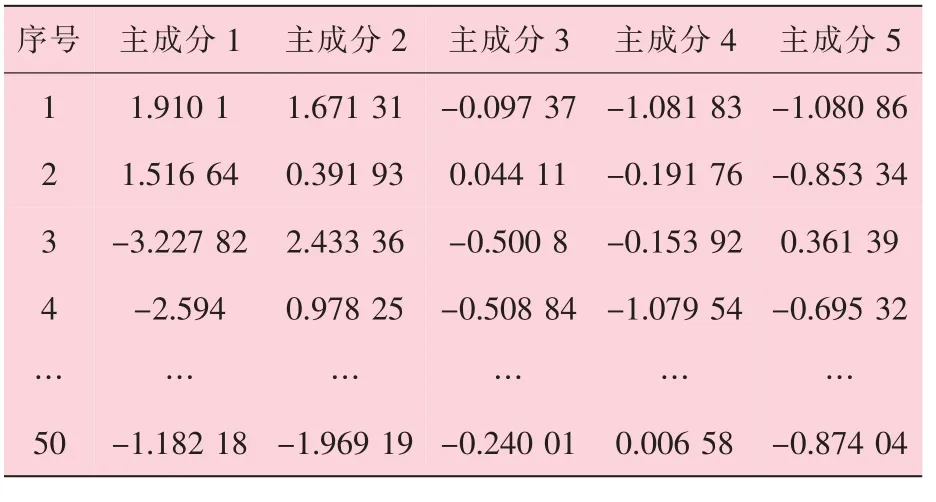
表3 重组后的样本数据
根据Kolomogorov 定理, 确定隐含层的节点数为15, 选取Sigmoid 函数作为激活函数, 对GA 种群进行初始化操作, 设置种群个数50, 交叉因子区间[0.5, 1], 变异因子区间[0.002, 0.005],最大迭代次数200, 对GA 算法的进化过程进行迭代计算, 迭代过程如图2 所示。 随着迭代次数的增加, 适应度函数ARV 不断减小, 改进前后的GA 算法分别在152 次和48 次达到收敛条件,稳态误差分别为0.186 1 和0.062 4, 说明改进后的GA 算法收敛速度更快, 寻优效果更好。
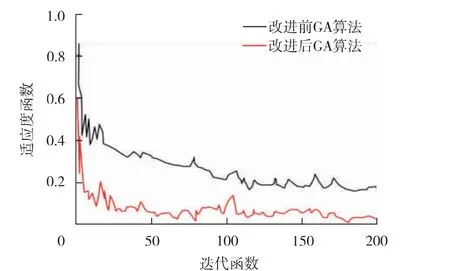
图2 GA 算法迭代过程示意图
为验证KPCA-GA-ELM 算法的预测精度,将预测结果与ELM 模型、 KPCA-ELM 模型和BP 模型进行对比, 验证集的预测结果见表4,不同预测模型的相对误差如图3 所示。
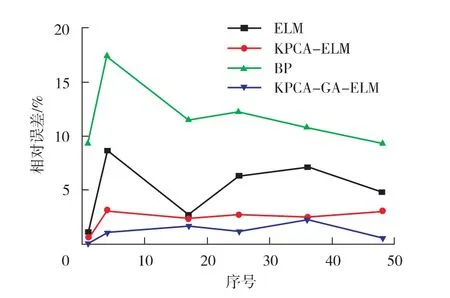
图3 不同预测模型的相对误差对比
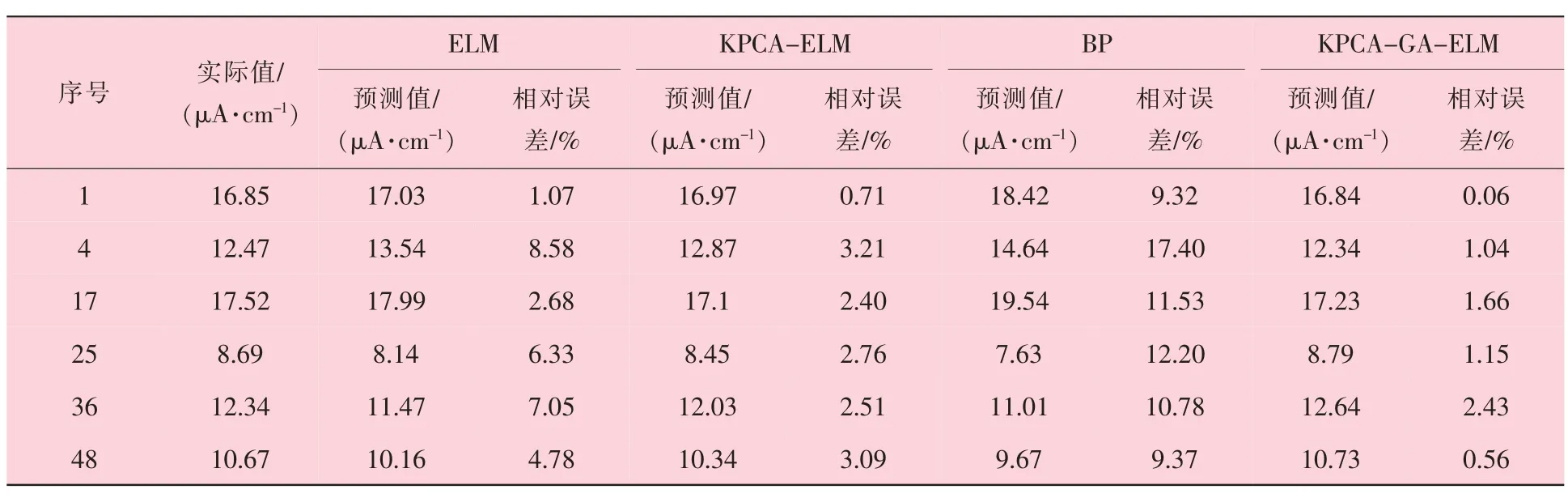
表4 不同预测模型的预测结果
由表4 和图3 可知, BP 模型的预测精度最差, 最大相对误差17.40%; ELM 模型由于权值范数较小, 减少了对网络中所有参数的迭代过程, 模型相对可获得更好的泛化性能, 故预测精度有所提高, 最大相对误差8.58%; KPCA-ELM模型对影响因素进行了数据降维, 避免了无效数据的使用和训练, 节省了算力, 预测精度进一步提高, 最大相对误差3.21%; 而KPCA-GA-ELM模型通过对ELM 模型参数的不断寻优, 预测精度最高, 其验证集样本内的相对误差均小于其余3 种模型, 最大相对误差为2.43%。
进一步分析4 种模型的MSE、 MAPE 和R2,见表5。 其中, KPCA-GA-ELM 模型的MSE 和MAPE 分别为0.148 33 和1.15, 均比其余3 种模型小, 且相关系数R2=0.998 8, 在模型中最大,说明KPCA-GA-ELM 模型的预测性能和鲁棒性较好, 可以用来预测海底管道外腐蚀情况, 可为有效评估管道完整性和制定维护策略提供实际指导。
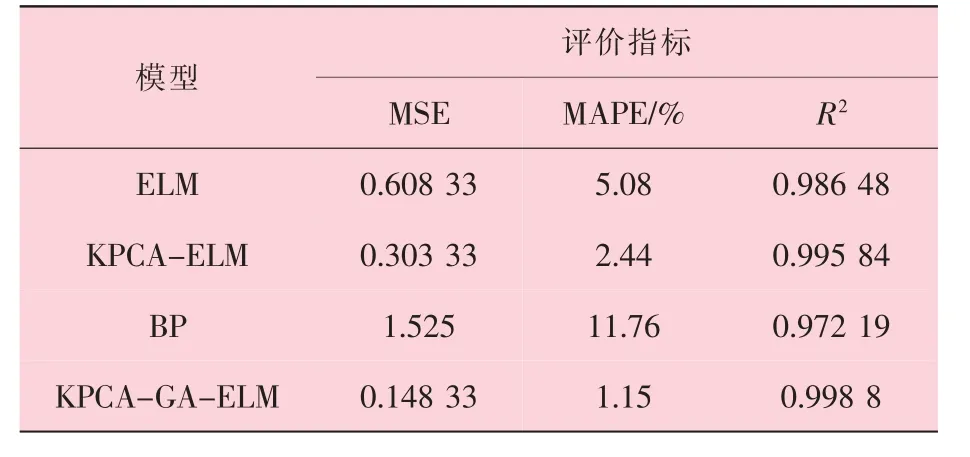
表5 不同预测模型评价指标对比
5 结 论
(1) 采用KPCA 对影响海底管道外腐蚀的海洋环境因素进行了筛选, 结合改进的GA 模型对ELM 模型的输入权值和隐含层偏差进行优化处理, 经实例验证, KPCA-GA-ELM 模型最大相对误差2.43%, MSE 和MAPE 分别为0.148 33和1.15, 预测精度最高;
(2) 在迭代的过程中, ELM 模型的隐含层节点数和激活函数采用经验确定, 但这两个参数对模型的计算结果影响较大, 今后应将此作为研究方向进一步优化模型算法。
