考虑应变率及密度影响的含铝PBX炸药本构模型
2021-12-06胡雪垚聂贻韬屈可朋
胡雪垚,聂贻韬,沈 飞,肖 玮,屈可朋
(1.西安近代化学研究所,陕西 西安 710065; 2.海装装备项目管理中心,北京 100071)
引 言
高聚物黏结炸药(PBX)因其配方灵活、加工便捷、力学性能优异等诸多优点,在常规武器战斗部及火箭推进剂中得到了广泛应用。在实际使用过程中,炸药装药会受到不同应变率的载荷作用,如:加工、装填及运输过程中应变率小于10-1s-1;发射过载和低速撞击时应变率约为10-1~102s-1;而高速撞击时应变率可超过102s-1。此外,由于加工工艺的限制,尤其是大尺寸的炸药装药结构,其不同位置处的装药密度不可避免地存在一定差异。然而,在不同密度分布和加载速率条件下,材料通常表现出截然不同的力学行为,严重影响炸药的安全使用。目前,数值计算是炸药装药安全性研究的重要方法,如何真实反映炸药材料在不同条件下的力学行为是高精度仿真的重要基础,为此,非常有必要建立能够准确描述其应变率及密度依赖性的本构模型。
PBX炸药是由高体积分数的含能颗粒和聚合物黏结剂组合而成的复合材料。其中,含能颗粒为弹脆性材料,在低应变水平下容易产生损伤;而黏结剂具有明显的黏弹性特征,其力学行为受应变率影响较大。孙文旭等[1]基于Z-W-T模型建立了考虑损伤的动态黏弹性本构模型,描述了不同应变率下PBX-1炸药的动态力学行为,但在准静态条件下未得到较高精度的拟合结果。Bennett等[2]在Dienes等[3]提出的统计裂纹力学模型基础上,发展了能够描述材料黏弹性力学响应和微裂纹损伤演化行为的Visco-SCRAM模型。该模型经过不断地应用和发展,已经能够描述含能材料的力学行为并预测其点火行为[4-5],但由于其形式复杂,在工程实践中并未得到广泛应用。
除了加载速率,炸药装药的力学行为还受到众多因素的影响,例如材料组分[6],微观结构[7]、加载条件[8]以及材料密度[9-10]等。且由于装药结构和加工工艺的影响,实际的炸药装药通常具有密度分布不均的问题,其动态力学响应行为非常复杂。陈荣等[9]研究了3种不同密度的PBX炸药在准静态和动态加载下的力学性能,并建立了能够描述材料高应变率下力学行为的本构模型。蔡宣明[10]研究了两种不同密度PBX炸药的压缩力学性能,发现材料的峰值应力随着初始密度的增大显著提高,并基于应变能函数建立相应的动态本构模型。尽管上述模型考虑了材料密度对力学行为的影响,但这些模型主要针对高应变率加载条件,无法兼顾准静态条件下材料的力学响应特性。众所周知,冲击响应通常是一个复杂的三维问题,不同位置处材料的受力状态和变形损伤速率往往不同。考虑到准静态和动态加载下材料力学行为及损伤演化等方面的显著差异,有必要发展一个能够描述较宽应变率范围内密度对PBX炸药力学行为影响的本构模型。
本研究主要针对RDX基含铝PBX炸药,制备了3种不同平均密度的样品,分别采用分离式Hopkinson压杆系统和电子万能试验机进行不同应变率下的压缩力学性能测试。分析了密度和加载速率对含铝PBX炸药力学行为的影响,建立了能够描述不同密度材料在较宽应变率范围内力学行为的本构模型,为装药工艺优化及安全性使用提供参考依据。
1 试 验
1.1 样品制备
含铝PBX炸药由西安近代化学研究所提供,其主要成分(质量分数)为: RDX,75%;铝粉,20%;黏结钝感剂,5%;理论密度为1.83g/cm3。试样采用模具压制成型工艺,基于实际应用需求,试样密度选择为1.65、1.70和1.74g/cm3,试样尺寸为Ф12mm×8mm。
1.2 静/动态压缩试验方法
准静态试验采用电子万能试验机进行,加载速率为4.8mm/min,应变率为0.01s-1。动态试验在分离式Hopkinson压杆(SHPB)系统上进行,子弹、入射杆和透射杆均采用直径为16mm的LY12铝杆,长度分别为150、1200和1200mm。采用SDY2107A型超动态应变仪和DPO4104型示波器记录整个加载过程中的脉冲信号。考虑到含能材料的破坏应变通常较小,试验中应用波形整形技术。一方面延长加载波的上升时间,使其远大于应力波在试样内部传播一次所需的时间,保证试样在破坏前达到应力平衡状态;另一方面过滤加载波中的高频分量,减小入射波波头的振荡信号和应力波弥散效应[11]。
2 结果与分析
2.1 密度和应变率对炸药力学性能的影响
为了分析密度和应变率对含铝PBX炸药力学行为的影响,分别针对3种不同密度状态的含铝PBX炸药进行了0.01、400、800和1300s-1应变率下的压缩力学性能测试。试验发现,由于铝的弹塑性和黏结剂的黏弹性特征,含铝PBX炸药的力学行为通常表现出一定的非线性。在低应变状态下,材料应力基本随应变线性增大,随着微裂纹的产生和不断累积,应力—应变曲线出现非线性变化趋势,直至达到最大应力后材料逐渐失去承载能力。图1分别对比了0.01s-1和800s-1应变率下,含铝PBX炸药的压缩应力—应变曲线随密度的变化规律。可以看出,在准静态和动态条件下,材料的峰值应力和弹性模量均随密度的增大而增大,其力学性能与材料初始密度密切相关。
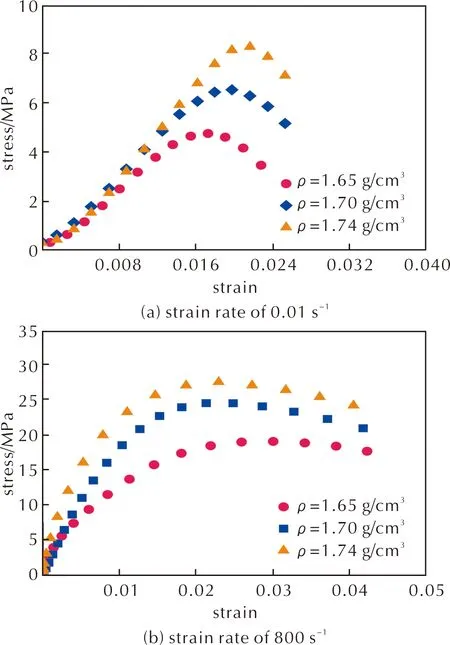
图1 不同密度含铝PBX炸药的应力—应变曲线Fig.1 Stress—Strain curves of aluminized explosive with different densities
为了进一步研究材料密度对其压缩力学性能的影响,图2给出了不同应变率下弹性模量和峰值应力随密度的变化曲线。
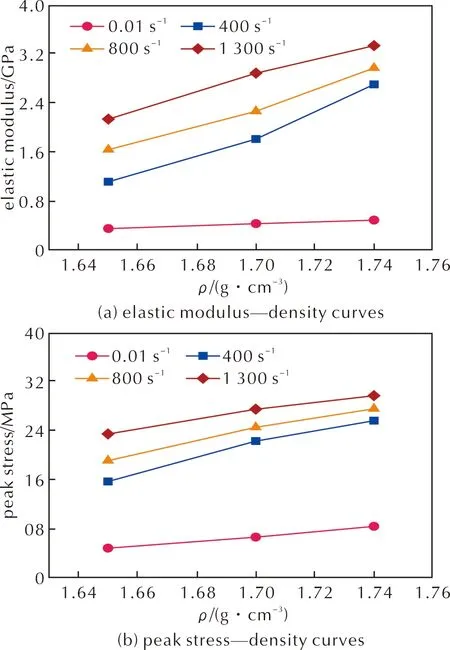
图2 不同加载速率下含铝PBX炸药弹性模量和峰值应力随密度的变化规律Fig.2 Varitations in elastic modulus and peak stress with increasing density of aluminized PBX explosive at different strain rates
由图2可知,随着密度的增大,压缩模量和峰值应力均表现出不同程度的提升,其中峰值应力的增大程度随应变率增加呈递减趋势,分别为74.89%、63.51%、44.46%和26.79%,且在准静态条件下,弹性模量和峰值应力随密度基本呈线性变化:
(1)
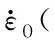
为了进一步确定含铝PBX炸药弹性模量和峰值应力的应变率依赖性,图3给出了固定密度状态下,材料模量和峰值应力随应变率的变化规律。
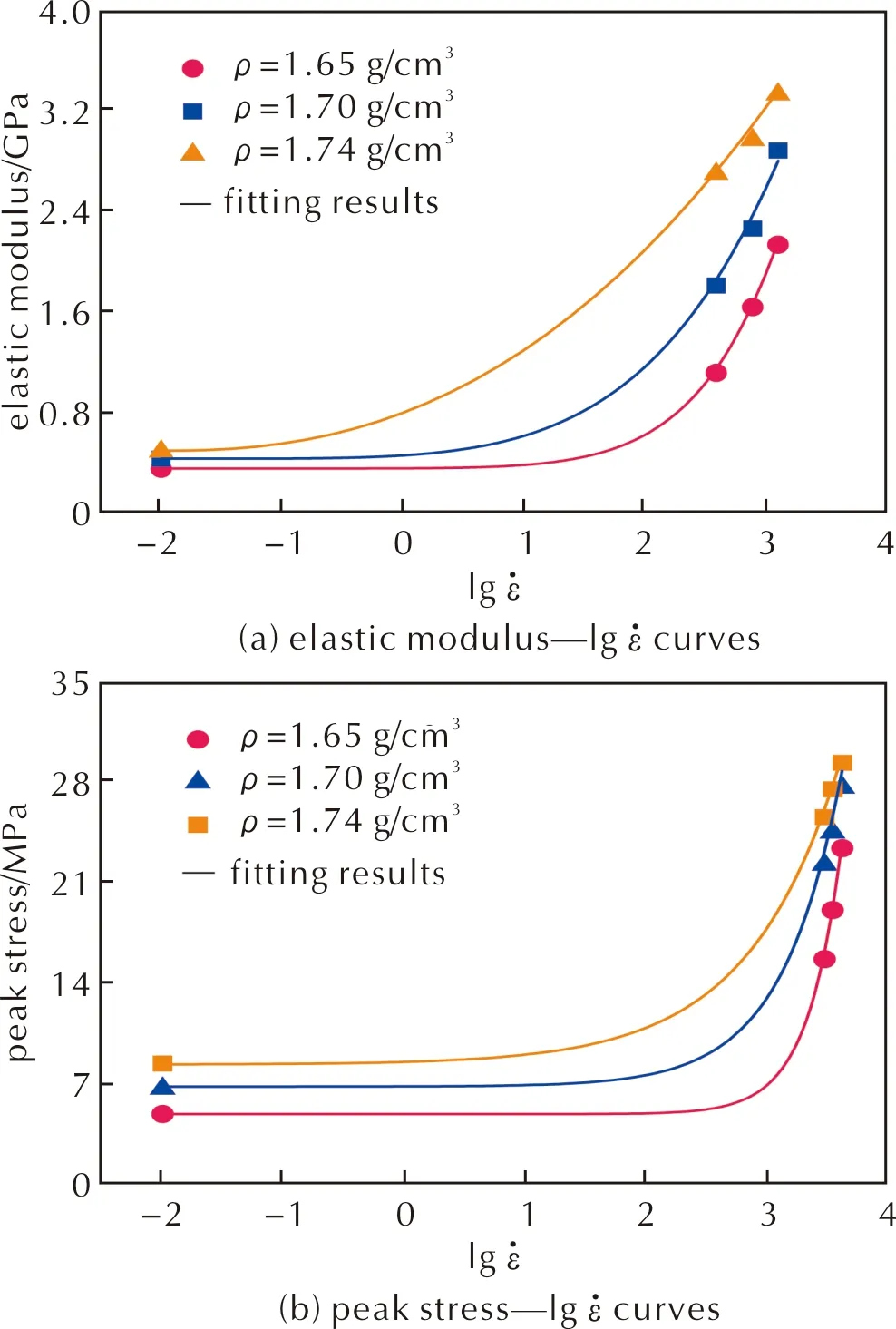
图3 不同密度状态下含铝PBX炸药弹性模量和峰值应力随对数应变率的变化规律Fig.3 Varitations in elastic modulus and peak stress with increasing logarithmic strain rate of aluminized PBX explosive with different densites
可以看出,随着对数应变率的增加,两者均表现出幂函数变化趋势,且可表示为[12]:
(2)
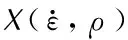

(3)
通过拟合发现,描述材料应变率依赖性的系数ax和bx并不是常数,而是随着材料密度不断变化的。且对于不同的材料参量,可统一表示为:
(4)
(5)
式中:α1、α2、β1和β2为材料系数。
拟合结果与试验结果对比如图4所示。将拟合得到的系数带入式(3),即可获得不同应变率、不同初始密度条件下含铝PBX炸药的弹性模量和峰值应力,对比结果如图3所示。可以看出,本研究建立的模型能够准确预测该含铝PBX炸药弹性模量和峰值应力随应变率和初始密度的变化规律。
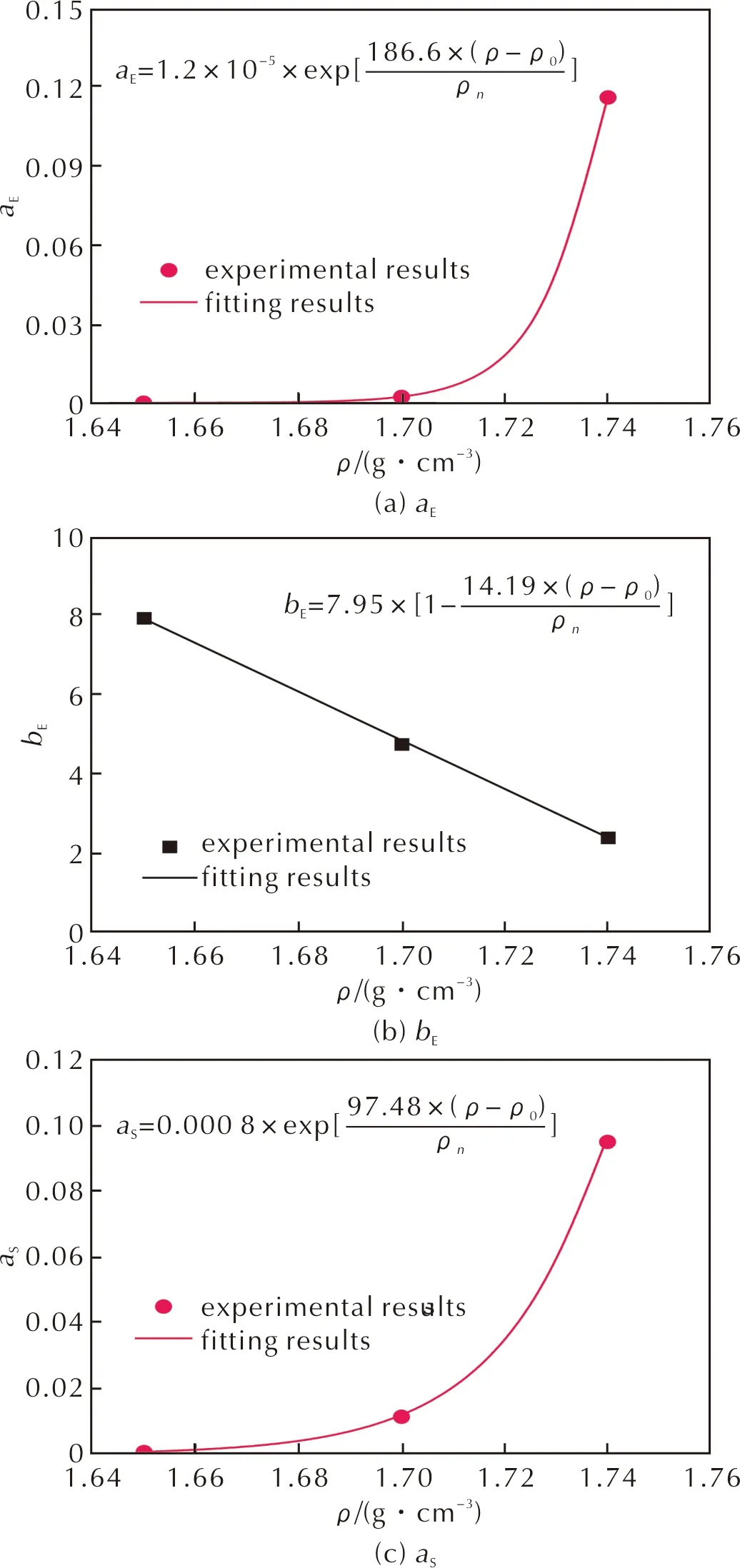
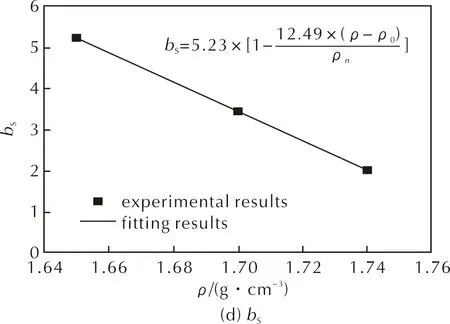
图4 不同模型参数随密度的变化规律Fig.4 Variations in different parameters with increasing the density
2.2 含损伤黏弹塑性本构模型
考虑到加载速率及初始密度对含铝PBX炸药力学性能的显著影响,其应力可表示为应变、应变率以及初始密度的函数。此外,材料密度在一定程度上反映了其内部的初始微观缺陷,显著影响着材料损伤演化阶段的力学行为。因此,考虑含铝PBX炸药的应变率及初始缺陷依赖性的本构模型具有如下形式:
(6)
式中:σ和σ0分别代表含损伤和不含损伤材料的应力;D(0≤D≤1)为损伤系数。
考虑到聚合物黏结剂的黏弹性特征,含铝PBX炸药的单轴压缩本构模型可表示为[13]:
(7)
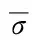
(8)
式中:γ为材料常数;I1为主应力张量第一不变量;J2为应力偏张量第二不变量。
在微观层面上,几乎所有的含能材料都是不均匀的,因此很难基于实际裂纹扩展规律来描述材料损伤演化对力学行为的影响。为此,本研究基于统计学方法定义了一个考虑初始缺陷影响的损伤系数[14]:
(9)
式中:S为材料的名义峰值应力;k为形状参数;e为自然数的底。
将式(8)、(9)带入式(7)并对等式左右两边积分,可以得到单轴加载条件下含铝PBX炸药的非线性本构模型:
(10)
将应变率和初始密度相关的弹性模量及峰值应力表达式带入式(10),即可得到单轴压缩条件下,该含铝PBX炸药考虑应变率敏感性以及初始密度依赖性的含损伤本构模型。拟合发现,形状参数k与应变率密切相关,可表示为[15]:
(11)
式中:d1、d2和d3为材料参数。
拟合曲线如图5所示。图6对比了通过模型拟合以及试验测试获得的应力—应变曲线,结果吻合良好,表明本研究建立的含损伤黏弹塑性本构模型能够准确描述较宽应变率范围内(0.01、400、800和1300s-1)、不同初始密度(1.65、1.74和1.74g/cm3)条件下含铝PBX炸药的压缩应力—应变行为,且通过适当修正和参数拟合,还可推广至类似具有应变率及密度依赖性的炸药材料当中。模型中所有参数见表1。
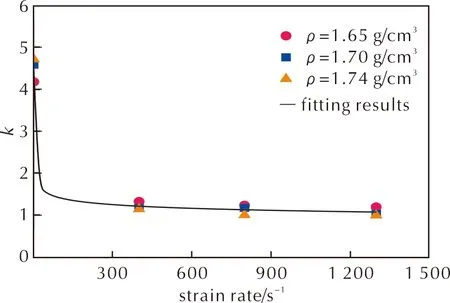
图5 参数k的拟合结果与试验结果对比Fig.5 Comparison of fitting results and experimental results for parameter k
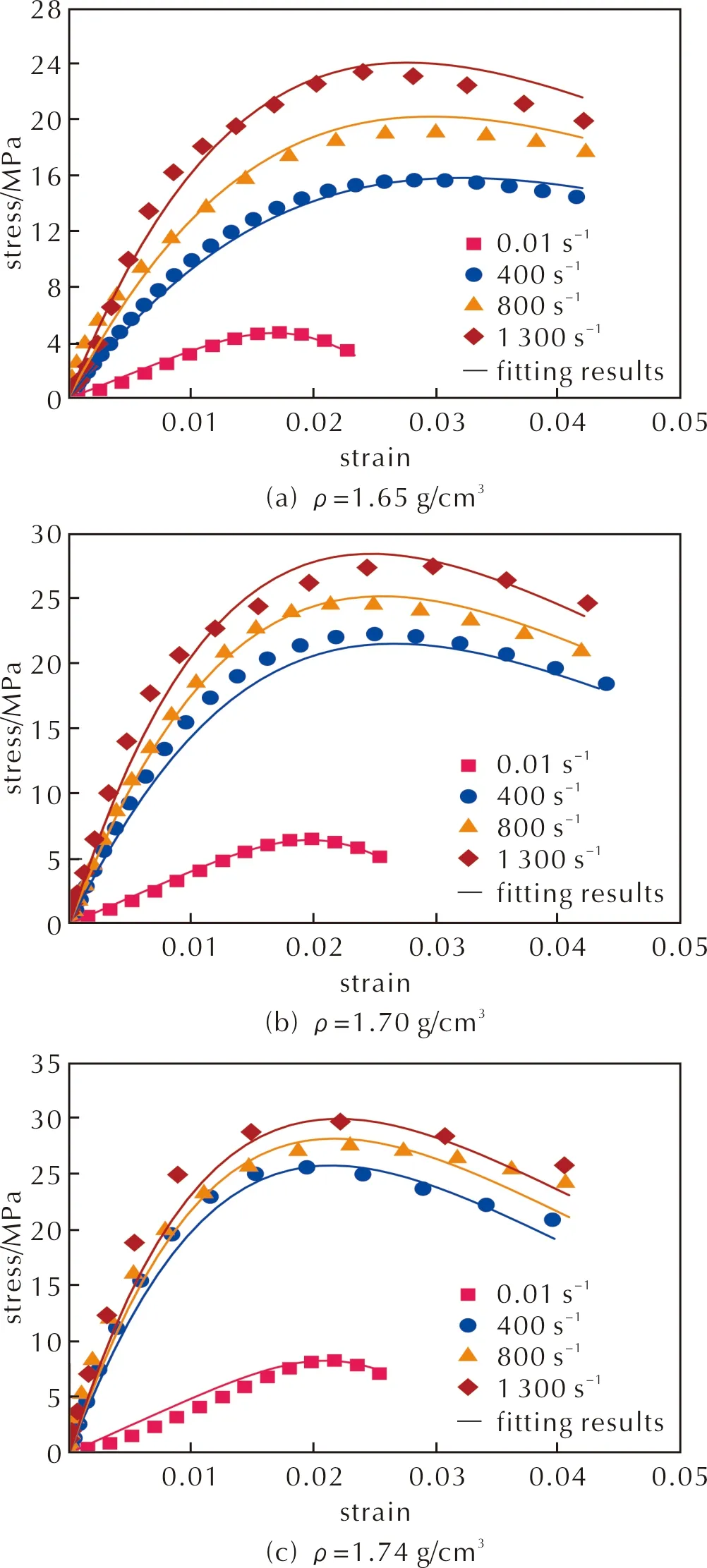
图6 不同密度及不同应变率下含铝PBX炸药的应力—应变曲线Fig.6 Stress—strain curves of aluminized PBX explosive with different densities at different strain rates

表1 含损伤黏弹塑性本构模型参数Table 1 Parameters of viscoelastic plastic constitutive model with damage
3 结 论
(1)该含铝PBX炸药的力学性能表现出明显的应变率和密度依赖性。压缩模量和峰值应力均随密度增大而增大,且随着应变率的增大,峰值应力的增大程度呈递减趋势,其中0.01s-1应变率下提升74.89%,而在1300s-1应变率下仅提升26.79%。
(2)考虑应变率和材料密度对含铝PBX炸药力学性能的影响,建立了含损伤的黏弹塑性本构模型,能够描述较宽应变率范围(0.01~1300s-1)内、不同密度状态含铝PBX炸药的压缩应力—应变行为,拟合结果与试验结果吻合良好。
