含能材料晶形预测方法：附着能模型及其发展

刘英哲

(西安近代化学研究所，陕西 西安 710065)

引 言

晶形控制是目前含能材料改性研究的重要途径之一[1]。对于相同的含能晶体，晶形能够在很大程度上影响感度、能量、流散性等性质[2-3]。例如，在相同尺寸下，球形晶体通常比其他晶形具有更高的装填密度和更低的机械感度[4-5]。然而，含能材料的晶形控制仍然较为困难，因为晶形生长不仅与晶体结构有关，还受到溶剂、温度、添加剂、结晶工艺等多种条件的影响。溶液结晶是含能材料最常用的晶形生长方式，但采用不同的溶剂时，得到的晶形差异很大[6]。

与基于“试错法”的结晶实验相比，通过理论方法预测晶形，有助于从微观上深入理解晶体生长机制，能够快速筛选溶剂、温度等结晶条件，从而为含能材料的晶形控制提供理论指导。当前，含能材料的晶形预测方法主要包括：Bravais-Friedel-Donnay-Harker (BFDH) 准则[7]、附着能模型[8-9]、占有率模型[10-11]、蒙特卡洛模拟方法[12-14]、界面结构分析模型[15]、螺旋生长模型和二维成核模型[16-19]等，这些方法的原理逐渐从结构因素、能量因素向生长机制演化，预测精度也逐渐增加。其中，附着能模型在考虑晶体结构因素的基础上，又引入了能量因素，预测结果相对准确，计算简单，又有很好的软件支持，成为含能材料领域中应用最广泛的晶形预测方法。

为此，本文综述了国内外近十年来附着能模型在含能材料中的应用情况，详细阐述了附着能的理论基础与计算方法，讨论了影响晶形预测结果的重要因素，并介绍了附着能模型的最新研究进展。

1 附着能模型理论与方法

1.1 基础理论

附着能模型基于恒定生长速率的简单假定[8-9]，即晶体中不同晶面的相对生长速率(Rhkl)与其附着能(Eatt)的绝对值成正比关系：

Rhkl∝|Eatt|

(1)

晶面的附着能绝对值越大，其相对生长速率越快，在生长过程中越容易消失。附着能定义为一层厚度为dhkl的晶片附着在晶面(h k l)上所释放的能量，可由式(2)进行计算：

Eatt=Elatt-Eslice

(2)

式中：Elatt为晶格能量；Eslice为晶片能量。对于稳定生长的晶面，附着能为负值。需要注意的是，不同晶面的Eatt需要在相同的化学计量下(如每分子、每晶胞)比较才有意义，目前在绝大部分文献中，Eatt的单位简写为kcal/mol，实际上完整的单位应为kcal/(mol·molecule)或kcal/(mol·unitcell)。

基于给定的晶体结构，通过计算不同生长晶面的附着能，可预测真空条件下的生长形貌。在溶剂条件中，溶剂将附着在生长晶面上，溶质在晶面上生长时要克服溶剂层的阻力，导致晶面生长速率受到抑制。为此，需要对附着能进行修正：

(3)

式中：Es为溶剂吸附所引入的能量修正项，表示溶剂对晶面生长的抑制作用；S为修正因子，体现了生长晶面的结构特征，可理解为不同晶面结构对Es的权重，其定义为:

(4)

式中：Aacc为晶面单元(h k l)的溶剂可及表面积；Ahkl为晶面单元的横截面积。显然，S值越大，晶面越粗糙；S值越小，晶面越平坦。Es可通过溶剂与晶面的相互作用能(Eint)进行计算：

(5)

式中：Abox为模拟盒子中生长晶面(h k l)的横截面积；Eint为晶面-溶剂体系的总能量(Etot)与晶面能量(Ecry)和溶剂能量(Esol)之差，即：

Eint=Etot-(Ecry+Esol)

(6)

在溶剂条件下，假定晶面的相对生长速率与修正后的附着能仍然成正比关系，即：

(7)

因此，通过计算溶剂中的修正附着能，即可预测晶体在溶剂中的生长形貌。为了便于理解溶剂条件下附着能公式中的相关计算参数，将其物理含义形象地表示出来，如图1所示。另外，基于类似的思想，也可将附着能模型进一步拓展至添加剂条件下[20-22]，此处不再赘述。

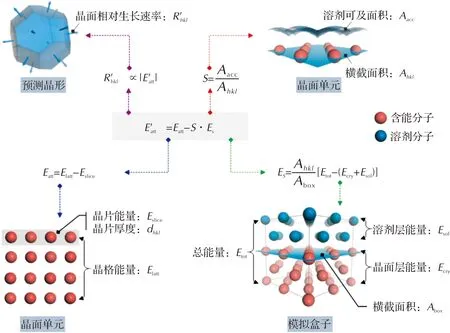
图1 溶剂中附着能计算公式示意图Fig.1 Schematic diagram of attachment energy calculation in solvent

1.2 计算模型

为了预测溶剂中的生长形貌，需要构建合理的晶面-溶剂界面模型，从而准确地计算附着能。图2为晶面-溶剂界面模型的构建示意图。首先，基于给定的晶胞结构，计算低米勒指数晶面的附着能，得到真空中的预测晶形和稳定生长晶面。然后，沿着每个生长晶面的(hkl)指数，对晶胞进行切割获得生长晶面单元，并构建超晶胞，从而获得三维的晶面模型。对于溶剂模型，可根据给定密度将溶剂分子随机地填充到三维盒子中。最后，沿着生长晶面的法向量方向，将溶剂模型“拼接”到晶面模型上方，形成晶面-溶剂界面的初始结构。在添加剂条件下，也可通过类似方法构建计算模型，但一般用单个添加剂分子替代溶剂层结构[23]。

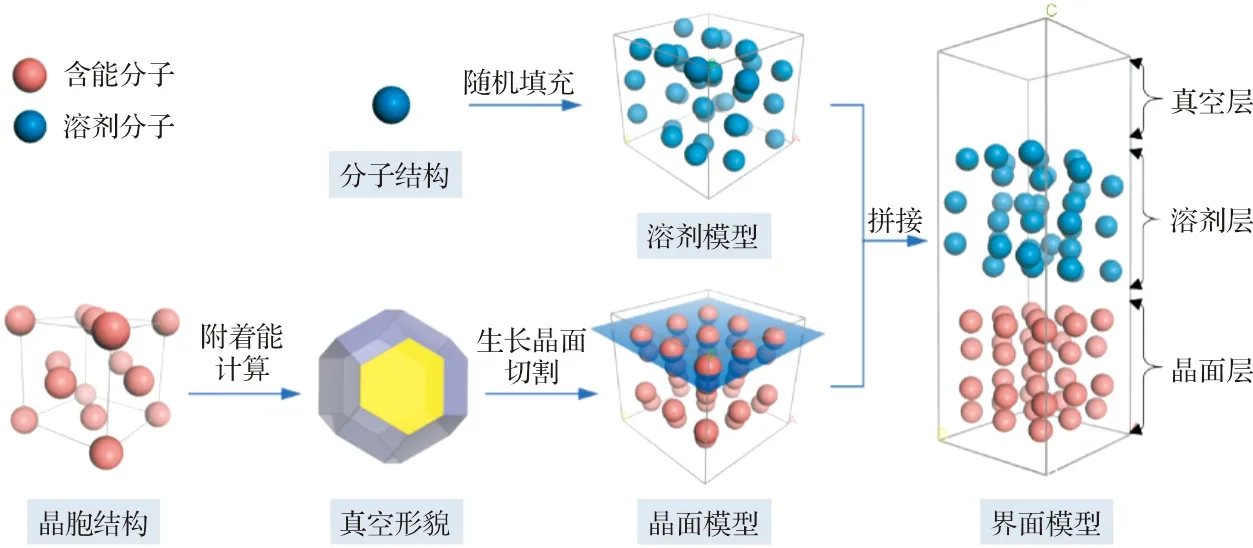
图2 晶面-溶剂界面模型搭建示意图 Fig.2 Scheme in construction of crystal-solvent interfacial model

随后，在NVT系综中对上述界面结构进行分子动力学模拟。由于施加了三维周期性边界条件，为了尽可能地避免溶剂与晶面的镜像发生相互作用，还需要在溶剂层上方设置一定厚度的真空层。真空层的厚度要大于非键作用的截断半径，通常为几十埃。另外，附着能模型假定生长晶面上不发生结构重排[8]，一般可在分子动力学模拟中固定晶面的位置。待界面体系到达平衡后，对模拟轨迹进行平均求得晶面-溶剂相互作用能，从而进一步计算溶剂中的附着能。

2 附着能模型在含能材料中的应用

2.1 在晶形预测中的应用

当前，附着能模型已经广泛应用于含能材料的晶形预测，研究体系包括常见的分子晶体、离子晶体和含能共晶，分别见表1、表2和表3。这些研究预测了含能材料在真空、(混合)溶剂、添加剂等不同生长条件的晶形，并讨论了温度效应对晶形生长的影响。此外，将附着能结果进一步结合径向分布函数、扩散系数等计算分析方法，从微观上揭示了溶剂与生长晶面的相互作用，为含能材料的晶形控制，甚至是共晶形成提供了理论支撑[24-26]。

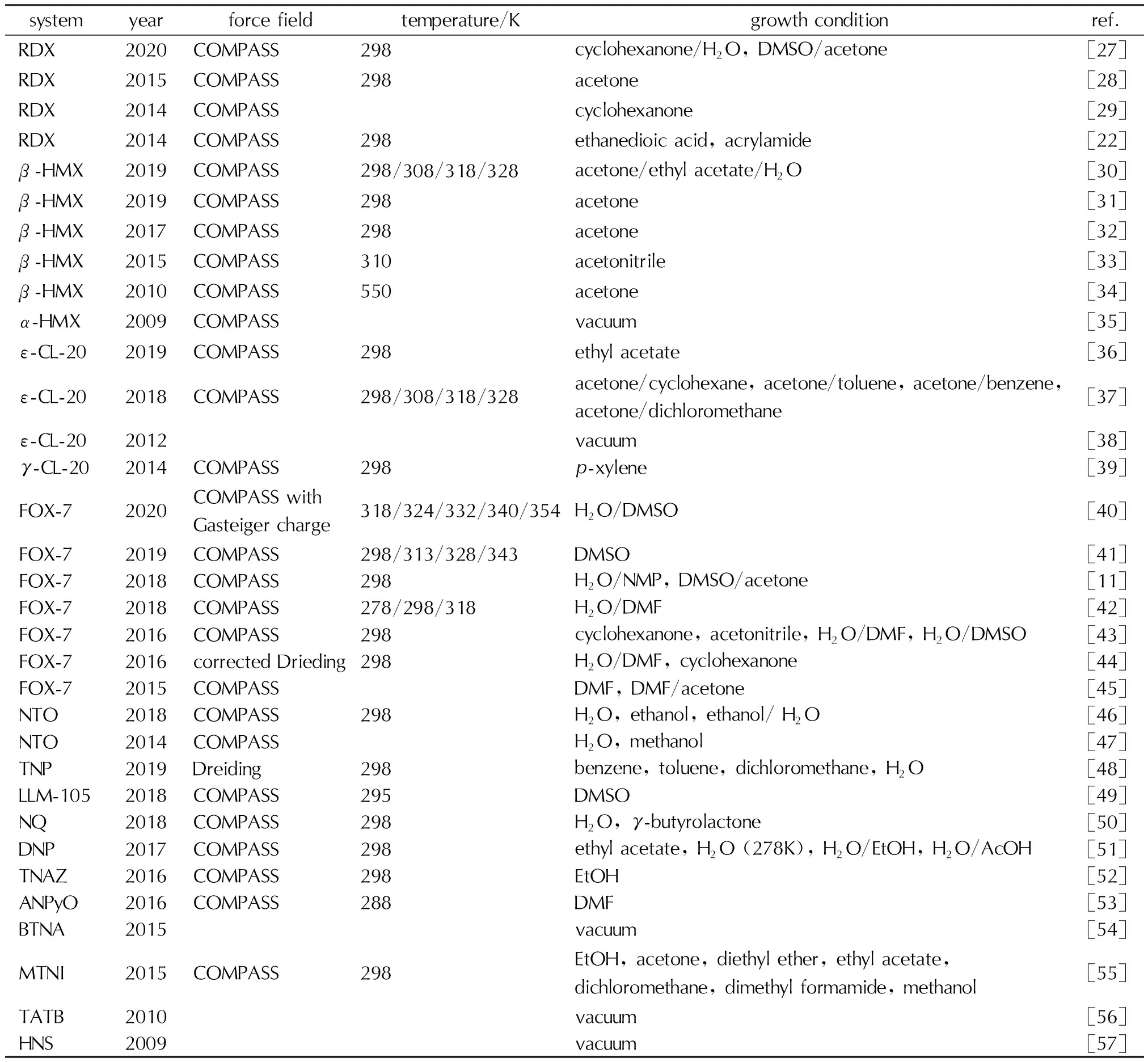
表1 含能分子晶体的晶形预测文献汇总Table 1 Summary on the morphology predictions of energetic molecular crystals

表2 含能离子晶体的晶形预测文献汇总Table 2 Summary on the morphology predictions of energetic ionic crystals

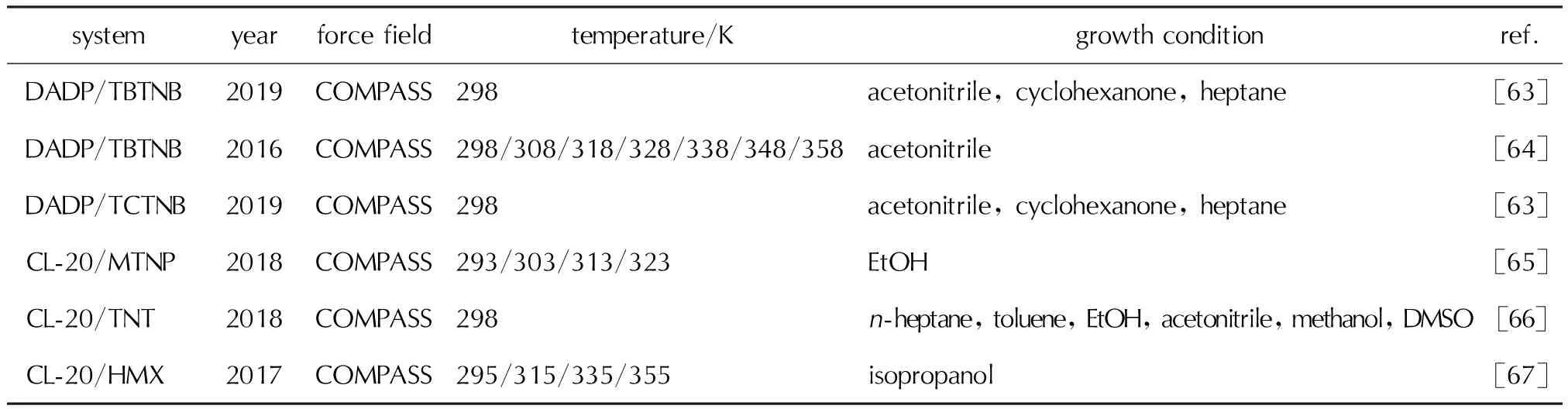
表3 含能共晶的晶形预测文献汇总Table 3 Summary on the morphology predictions of energetic cocrystals

2.2 不同计算结果间的差异

对于大部分含能晶体，附着能模型能够从定性上给出与实验数据相吻合的预测结果。然而，从相同体系的预测晶形预测对比图(见图3)可以看出，有时附着模型预测的晶形也存在一定差异。尽管附着能模型的理论假设非常明晰，但附着能的计算结果受很多因素影响，如力场参数，模型尺寸，晶面-溶剂相互作用能等，这都将直接决定晶形的预测结果。因此，如何准确地计算附着能是一个关键问题。

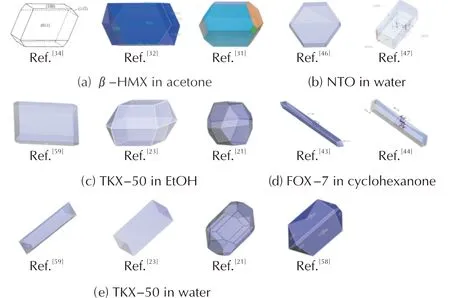
图3 相同体系下的晶形预测结果对比Fig.3 Comparison on the morphology predictions of same systems

3 附着能的准确计算

3.1 Eatt的计算

从附着能的定义上看，附着能的本质是相互作用能。因此，在实际计算过程中，真空中的附着能可通过式(2)求得：

(8)

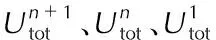
为了准确计算附着能，需要考虑其随着晶面厚度的收敛情况。如图4所示，可计算一系列不同厚度的晶面能量，当其能量差趋于稳定时，则附着能达到收敛。此处以β-HMX晶体为例，晶胞的Z值为2，5个生长晶面(0 1 1)、(1 1 0)、(0 2 0)、(1 0 1)和(1 0 -1)的Z值分别为2、2、1、2和2。

图4 真空中附着能计算示意图 Fig.4 Schematic diagram of attachment energy calculation in vacuum

表4给出了真空中HMX生长晶面的附着能随晶面厚度的变化情况[31]。不同晶面的附着能对晶面厚度的收敛情况是不同的。显然，当晶层厚度不足时，附着能计算偏差较大。对于HMX晶体，当n≥6时，所有晶面的附着能都已收敛，与Materials Studio软件[68]给出的结果基本一致。另外，考察附着能随晶面厚度的收敛情况，也可为界面模型中晶面层厚度的构建提供参考。

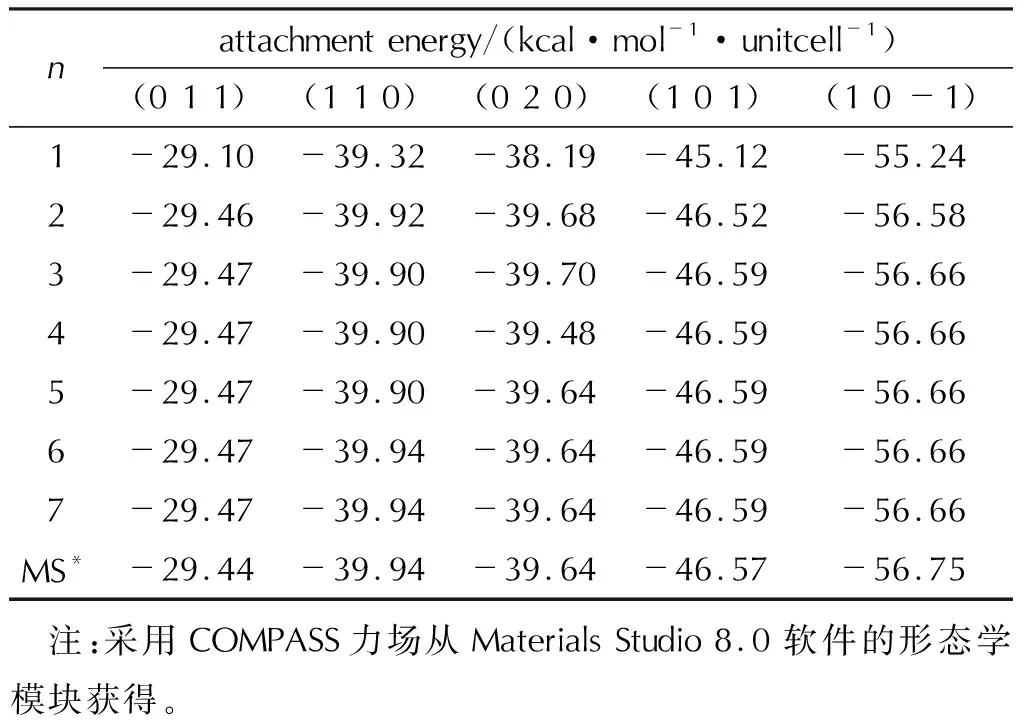
表4 真空中HMX生长晶面的附着能随晶面厚度的变化情况Table 4 Attachment energies of HMX growth faces in a vacuum as a function of crystal layer thickness (unit: kcal/mol/unitcell)

3.2 力场参数

附着能的计算是基于分子力场完成的。因此，在开始计算附着能之前，要对力场参数的可靠性进行评价。选择合适的分子力场是准确计算附着能的基础。通常，可将拟选用的分子力场用于晶体结构优化，根据优化后的晶格参数与实验数据的偏差，对力场的准确性进行验证。此外，也可基于分子力场计算晶格能，与其实验值进行对比。晶格能可通过实验测定的升华焓(ΔHsub)数据进行求解[8,29]：

Elatt=-ΔHsub-2RT

(9)

式中：R和T分别为气体常数和温度；2RT为校正因子。晶格参数与晶格能考察的主要是分子间作用参数，同时也要注意晶体优化后分子结构是否发生较大变化。另外，可通过溶剂密度计算来验证分子力场对溶剂的兼容性。

COMPASS力场[69]是目前含能材料领域中应用最广泛的力场，可适用于绝大部分CHON含能分子。然而，随着近年来新型含能化合物的陆续合成，有一些特殊的成键类型，难以用COMPASS力场描述，比如TKX-50中的N→O键。表5对比了COMPASS、PCFF[70-72]、CVFF[73]3种力场对TKX-50晶格参数的优化结果[23]。从表5可知，COMPASS力场优化的晶格参数与实验数据相差较大。CVFF力场优化的b轴长度与实验值也存在较大偏差。相比之下，只有PCFF力场的优化结果与实验结果较为接近，因此被用于描述TKX-50晶体[21,59,60]。

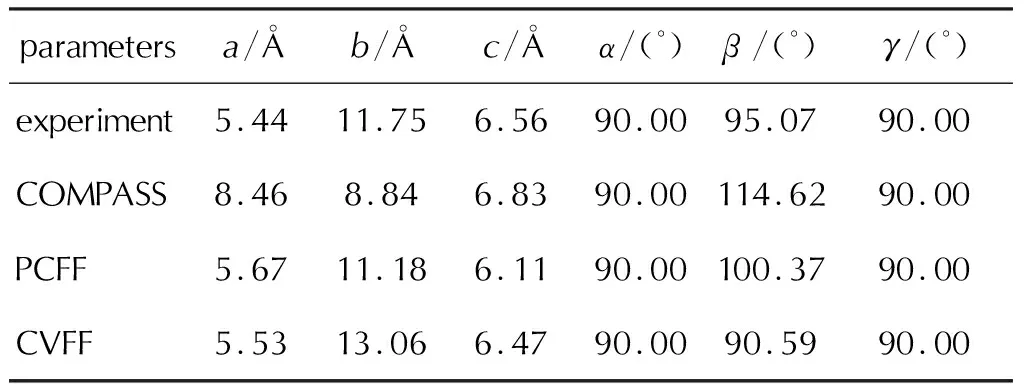
表5 不同力场优化下的TKX-50晶格参数Table 5 Lattice parameters of TKX-50 crystal optimized by different force fields

需要注意的是，TKX-50是一种含能离子盐，正负离子之间存在很强的静电相互作用，对生长晶面的附着能影响很大。在PCFF力场中，TKX-50的正、负离子分别带有+1e和-2e的电量，与量化计算结果+0.82e和-1.64e不相符[74]。因此，可通过密度泛函理论GGA-PBE/DNP对TKX-50晶胞进行电荷布居分析，将Mulliken电荷作为原子电荷，进一步修正TKX-50晶体内的静电作用。经该参数优化后，TKX-50的晶格参数变为a=5.45Å,b=10.89Å,c=6.23Å,α=90.00°,β= 8.44°,γ=90.00°，与实验数据也较为相近。

表6汇总了真空下TKX-50的晶形预测结果。同样采用PCFF力场描述TKX-50时，晶形预测结果也略有不同，但主要生长晶面和长径比基本相同。对PCFF力场的电荷参数修正后，晶形与生长晶面发生了较大变化。另外，COMPASS力场计算的晶形类似于纺锤状。由此可见，晶形预测结果对力场参数较为敏感。

除了TKX-50，刘宁等[44]对FOX-7的Dreiding力场参数[75]进行了部分修正，使晶格参数的相对计算误差在5%之内；Song等[40]结合COMPASS力场和Gasteiger电荷，进一步将晶格参数的相对计算误差控制在3%以内，均比COMPASS力场(7%)有了一定提升[41]。另外，Song等[76]结合COMPASS力场参数和RESP电荷描述DNTF晶体，晶胞参数的最大相对误差仅为-2.86%，相比之下，采用COMPASS力场中的默认电荷时，晶胞参数的最大相对误差达-6.00%[77]。

3.3 模型尺寸

在分子动力学模拟中，模型尺寸也是一个影响附着能计算结果的重要因素。显然，模型越大，附着能计算越精确，耗时越长。相反，模型尺寸也不能过小，至少要大于非键作用截断半径的两倍，以避免周期性边界条件下分子与其镜像发生相互作用[78]。因此，如何搭建合适的模型体系，在准确性与耗时性上取得平衡，是一个需要考虑的问题。在构建晶面-溶剂界面模型时，研究人员通常采用3×3×3超晶胞的晶面模型和几百个分子的溶剂模型，并没有一个通用的构建规则。

为此，Li lijie等[30,36,37,41,46]系统研究了模型尺寸对附着能计算结果的影响，包括晶面层、溶剂层、真空层的厚度以及模拟盒子的长度和宽度。首先，考察了非键作用能随截断半径的收敛情况，认为非键作用的截断半径(dc)选取15.5Å较为合适。然后，分别计算了溶液中附着能随晶面层、溶剂层、真空层厚度和模拟盒子长度、宽度的变化。最后，通过对β-HMX、FOX-7、ε-CL-20、NTO多种含能材料的测试，给出了一个合适尺寸的模型构建规则：晶面层的长度、宽度和厚度应大于2dc、2dc和dc，溶剂层和真空层的厚度应大于dc，即模型尺寸应在图5填色区域之外。基于该模型尺寸，溶液中生长形貌的预测结果与电镜数据极为吻合。

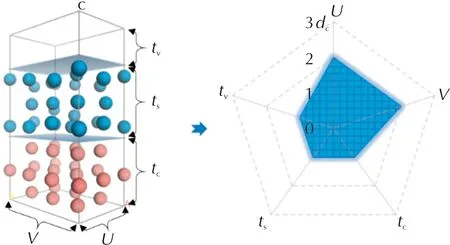
图5 模拟盒子的建议尺寸 Fig.5 Suggested size of simulation box

3.4 Eint的计算

探索溶剂在晶面上的微观吸附行为，有助于理解溶剂效应对晶面生长的影响，从而更加准确地计算晶面-溶剂相互作用。研究表明[24,31,63,67,79-82]，在晶面-溶剂作用的影响下，溶剂在晶面上呈现出了典型的结构特征——层状分布。此处，以HMX和丙酮溶剂为例，进一步阐述溶剂的吸附特点。

图6展示了丙酮溶剂(红色)和HMX(黑色)沿生长晶面(0 0 1)法向的质量密度分布情况[31]。显然，溶剂分子在HMX晶面法向上并不是均匀分布，而是呈层状分布。随着溶剂分子与HMX晶面法向距离的增加，溶剂峰的波动逐渐减小，直至局域密度趋于体密度，说明此处溶剂分子已经不受晶面作用的影响，与体相中的分布一致。因此，若要完整体现出溶剂在生长晶面上的结构排布，溶剂层需要具有一定的厚度。尽管不同晶面结构会导致局域密度有所不同，但均呈现出层状分布的特征。

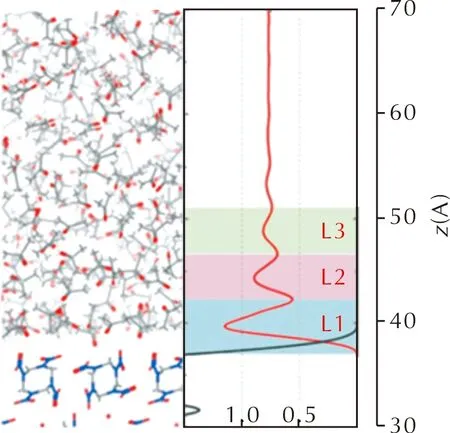
图6 沿晶面法向的质量密度分布Fig.6 Mass density profiles along the normal to the crystal face

为了分析层状分布对晶面-溶剂相互作用能的影响，根据溶剂峰的个数将整个溶剂层进行分层，如图6中为L1、L2和L3的色块，然后分别计算区域L1、L1+L2、L1+L2+L3和整个溶剂层与生长晶面的相互作用能。对于HMX和丙酮体系，HMX晶面与溶剂层L1的作用能约占总相互作用能的90%以上。基于不同溶剂层的Eint，最终预测的晶形结果较为相似，只是长径比略有不同[31]。

需要注意的是，在动力学模拟过程中，个别溶剂分子由于自由扩散作用可能会吸附在生长晶面的镜像上，为了确保计算精度，在计算Eint时要将这些溶剂分子剔除。如果采用了“三明治”计算模型，即生长晶面上下均有溶剂层，则不存在这个问题[76]。同时，还应注意附着能的化学计量。在真空中计算附着能时，若以晶胞为计量单位，需要将能量校正项Es转换为与Eatt相同的单位。

4 附着能模型的发展

4.1 溶剂效应的校正

如何更加合理准确地描述溶剂效应对生长形貌的影响是附着能模型发展的一个方向。从式(2)可知，能量校正项Es体现了晶面与溶剂的相互作用，校正因子S相当于生长晶面结构带来的权重。值得注意的是，Eatt和Es的本质都是相互作用能，区别在于：前者是晶面与生长晶片的相互作用，而后者反映了晶面与溶剂的相互作用。然而，在真空中计算Eatt时，并没有用S进行校正。因此，在溶液中计算附着能时，也不应采用S对Es进行校正。这是因为：在计算相互作用能时，已经隐含了晶面结构的影响，即晶面越粗糙，相互作用的接触面积也就越大，同样条件下的相互作用能也就越强，无需进一步修正。

为了更好地解释说明，定义了接触面积：

(10)

其中，Atot、A1和A2分别为体系和所包含组分的溶剂可及表面积。以HMX为例，计算表明，在真空中和溶剂中，晶面分别与生长晶片和溶剂的接触面积几乎是一样的[31]。因此，在同样的接触面积下，生长晶面在真空中的相互作用能Eatt和在溶剂中的相互作用能Es的计算标准应是一致的。实际上，校正因子S对晶面-溶剂相互作用额外加了权重，将对溶剂中的附着能带来一定偏差，特别是结构相对粗糙的生长晶面，有时可能使得附着能为正值，致使晶面不稳定。最近的研究基于这一新的校正公式，对溶剂中HMX的晶形进行了预测，计算结果与实验结果吻合较好[30-31]。

4.2 过饱和度的探索

附着能模型假设晶面的生长速率与附着能成正比，即每个晶面的生长速率是恒定的。因此，从原理上讲，附着能模型难以处理生长速率变化显著的生长条件，如过饱和度等[7]。

最近，Li lijie等[30,37]在构建溶剂层时，将一定数量的溶质分子也添加在内，研究了过饱和度对β-HMX和ε-CL-20在溶剂中生长形貌的影响。过饱和度(δ)可通过式(11)在模型构建时进行计算：

(11)

式中：C为计算模型中溶质的实际浓度，由溶剂层中溶质和溶剂的数量决定；C0是实验测定的饱和浓度。晶形预测结果表明，不同的过饱和度对形貌的长径比影响较大。由于结晶实验中的过饱和度很难保持不变，因此晶形预测结果尚不能与实验结果进行对比。

4.3 晶形预测新策略

图6表明溶剂沿生长晶面法向呈层状分布，当溶剂分子远离晶面一定距离后，其与晶面的作用可忽略不计，此时溶剂可看作自由扩散。当溶剂距离晶面较近时，溶剂吸附在晶面上，对溶质在晶面上的生长起到一定阻碍作用。

最近的分子动力学模拟表明，溶剂分子能够长时间地停留在晶面上的某些特定位置(吸附位点)[82]，具有最强的结合能力，对溶质生长的阻碍作用最大，这说明溶剂与晶面的相互作用也是不均匀的。然而，在计算溶液中的附着能时，溶剂效应是通过“平均化”的晶面-溶剂相互作用能来描述的(见式(6))。这种溶剂层与晶面层的相互作用并不能真正体现出对溶质生长最为重要的抑制效应。

实际上，吸附位点处的结合能可以看作是“木桶效应”中的最短板，是决定晶体生长速率的关键因素。图7给出了晶体表面生长过程的示意图。由于溶剂在吸附位点处的结合能力最强，溶质将吸附位点处的溶剂替换则可以看作是晶面生长的“限速”步骤。为此，基于附着能模型的理论框架，提出了晶形预测新策略，即采用吸附位点处溶剂与溶质的结合能代替晶面-溶剂相互作用能，采用吸附位点处溶质与溶质的结合能代替真空中的附着能，具体计算细节可参考文献[82]。显然，相比于溶剂中原有附着能的计算，从晶体生长过程上看，这种策略更加合理。基于该策略，预测了HMX在丙酮溶剂中的晶形，计算结果与实验结果吻合良好[82]。

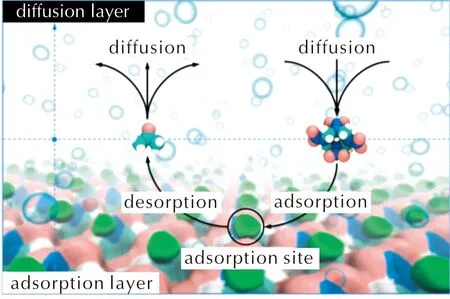
图7 晶体表面生长过程示意图 Fig.7 Scheme in the crystal growth process in solvent

5 结束语

附着能模型是目前含能材料领域中应用最为广泛的晶形预测方法，能够定性地给出溶剂、温度等不同条件下的生长形貌，可为含能材料的晶形控制提供理论参考。在使用附着能模型时，需要充分考虑力场选择、模型构建、溶剂效应等因素，从而准确地计算附着能。否则，相同体系的预测结果也可能会存在差异。值得注意的是，附着能模型仅仅基于恒定生长速率的简单假设，尚不能考虑结晶实验中的诸多因素，预测晶形有时与实验结果偏差较大也是合理的。为此，仍需进一步发展基于生长机制的晶形预测方法。