指向数学关键能力培养的深度思考实现路径
2021-12-03陈赛
陈赛

摘 要:深度思考是数学课堂的灵魂,是培养学生数学关键能力的核心要素。要培养学生数学关键能力,教师就需要从引发学生深度思考的角度设计和实施教学,通过创设有思考价值的问题情境,开展思行结合的自主探索,实施有教师指导的合作交流,展开有梯度的引导质疑等路径促进学生深度思考。
关键词:小学数学;深度思考;数学关键能力;核心素养
中图分类号:G623.5 文献标识码:A 文章编号:1009-010X(2021)28-0031-03
数学关键能力是数学核心素养的核心成分,它主要包括运算能力、空间观念、推理能力、抽象能力等等,培养数学关键能力是数学核心素养培育的重点,也是数学课堂教学的重要任务。因此,一线数学教师要在培养学生的关键能力时,让学生反复经历从事物的外部现象逐步深入事物内部本质层面,掌握知识的核心概念,并运用概念和深化概念的过程。在这个过程中深度思考,促进学生更深入地理解、沟通知识间的联系,建立起良好的知识结构,同时形成数学关键能力。可以说,深度思考是数学课堂的灵魂,它贯穿高效课堂的始终,是培养学生数学关键能力的核心要素。在数学教学中,教师要创造有利于启发学生深度思考的场域,让学生在深度思考中培养数学关键能力。
一、深度思考源于情境——创设有思考价值的问题情境,让思考从模糊走向清晰
(一)营造情景体验场,开启深度思考的阀门
小学生注意力容易被有趣的问题情境吸引。在教学时教师要密切联系学生的生活经验,创设具有思考价值而又有趣的问题情境,让学生在认知冲突中激发探索问题的兴趣,开启深入思考的阀门。
在教学“分数的初步认识”时,教师创设了猪八戒吃饼的故事情境:猪八戒到一个农民家里要饼吃,吃了三个饼,还没有吃饱。接下来,猪八戒想好了一个形状,但不知如何表达,只是说“我只要一小块儿”。教师适时问道:“一小块儿究竟是多大呢?”,学生默想一会,接着出示3张同样大的圆形纸片,让三位学生上来撕一撕。经过比较同学发现,虽然都表示“一小块儿”,但是三位学生撕的形状有别、大小不一。为什么会这样?
(二)设置问题驱动链,建构个性化知识结构
深度思考使他们不断地找出有联系的信息并进行整合、迁移、转化,让思考逐渐从模糊走向清晰,最终完成个性化的知识建构。
思考后他们明白了由于“一小块儿”说的太模糊了,表达不清晰,加上每个人对一小块儿的理解不一样,所以撕出来的纸片大小也不一样。紧接着,教师再出示一个圆形图,平均分成四块,其中一份涂上颜色,这时教师问:“你能够用精确的语言或者用一个数,把现在涂色的这一块表示出来吗?”学生陷入了深度思考。
认识分数,是数概念的一次拓展,对于三年级学生而言,难度较大,但教师呈现猪八戒要饼的问题情境,让学生置身于认识的冲突与困惑之中,从而感受到这“一小块儿”不能再用原来学过的数表示,必须用一种新的标准或者数来表示。当出示“一小块儿”图形后,学生们得以从不同的视角去解释,表达对一小块图形(就是四分之一的圆)的认识与理解。这个学习情境中,既有动手操作,也有比较分析,同时贯穿着学生积极的深度思考,达成了理性与感知的对接。学生认识由原来的模糊,经过点拨和引领,学会了从数学的视角去观察和思考,从而逐渐接近分数意义的核心部分,走向数学化的清晰。
二、深度思考融于探索——开展思行结合的自主探索,让思考从片面走向全面
把思考融入到动手操作和自主探索中,能够促进学生在体验中从感性走向理性,结合具体的分析问题、探索问题和解决问题的过程,逐渐地打开思路,在已知和经验基础上,不断完善知识网络,形成良好的知识结构。在不断的甄别、论证、探索过程中,他们的思考也会由片面走向全面,合情推理能力得到有效提升。
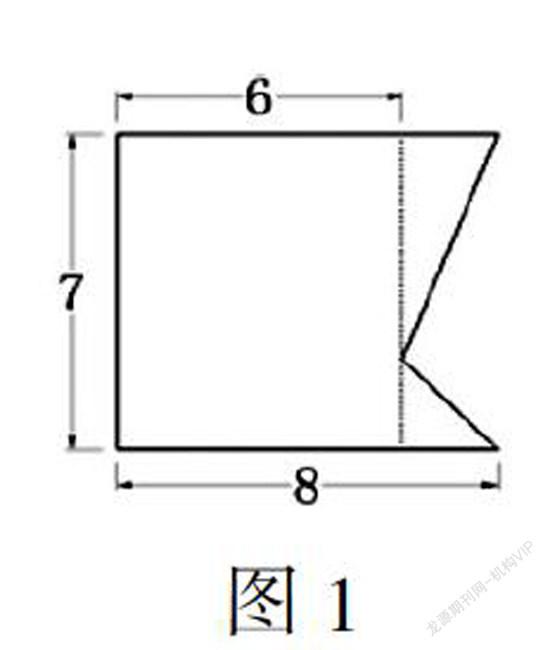
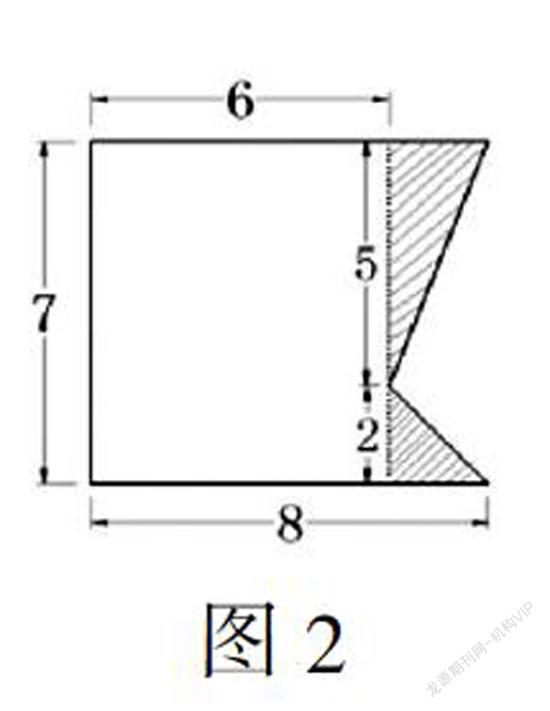
在计算下面图形(单位厘米,如图1)的面积时,学生先独立尝试计算,小组交流后汇报。汇报中出现了很多不同的算法,其中一种把图中右下角的小三角形看成底和高都为2厘米的等腰直角三角形来计算(如图2),教师提出质疑:这种做法结果是对的,但是有没有道理呢?
在辩论和深度思考中,学生借助画图和列举,计算发现了下面的小三角形高即使不是2厘米,而是3厘米、4厘米或者5厘米,结果面积都一样。还有学生出示了以下几个图形(如图3~6),并介绍:如果增加一条辅助线,两个三角形和涂色部分正好组成了一个小长方形。这样,不论把涂色三角形的顶点移到哪里,涂色大三角形面积都与两个小三角形面积的和一样多,涂色部分三角形的底和高是不变的,它的面积是组成的长方形面积的一半。
学生通过自己动手实践,亲历了探究和论证一个与众不同做法的对与错。从把小三角形看成高是2厘米的片面认识中,通过列举和画图的办法逐步发现各种不同图形中的内在联系,借助直观操作把复杂的问题简单化,让思考从片面走向全面,在这样的教学中,学生不仅能够提高解决问题的能力,还能够发展他们的几何直观与合情推理能力。
三、深度思考精于对话——实施有教师指导的合作交流,让思考由无序走向合理
教师指导下的交流对话能够让学生互相分享体验、交流感悟,从而产生智慧的碰撞。面向全班的展示汇报,能够示范好的做法,也能够暴露出学习中存在的障碍,让教师及时了解和掌握学生的思维状况,然后根据学情及时点拨引导,有的放矢地持续推进学生对问题的思考,让学生的思考从无序走向合理,在自我建构整体知识结构的过程中培养学生关键能力。
教学“解决问题的策略——列举”时,在学生自主学习阶段,有的学生把题意理解错误,把“用22根1米长的小棒围成一个长方形”理解成一个长加一个宽就等于22米;也有的只画了几个长方形,并没有列举完全,就在画的图形中选出最大的一个面积作为结果;还有的学生知道周长一定的时候,长和宽最接近时面积最大,一步想到最大的长方形长6米,宽5米。总之,大部分学生还只停留在问题解决的表层,并没有深入地去思考该如何更合理有效地解决类似问题,也没有激起用列举方法去解决这类问题的需求,更没有思考如何列举才能够既不重复,也不遗漏。
在汇报展示环节,教师有意识安排学生从错误到正确,从重复遗漏到完整全面,从无序到有序来依次汇报。在汇报过程中,教师针对学生出现的思路上无序、混乱等问题,适时地加以引导、追问、点拨,帮助学生体会和理解,从而明确这类问题该如何进行思考,如何避免重复和遗漏,使学生的思考逐渐地由无序散乱走向有序合理,从而真正体会到一一列举的价值。
四、深度思考深于质疑——展开有梯度的引导质疑,让思考由肤浅走向深刻
教学中教师通过主问题+问题串的方式,对核心问题展开有梯度的质疑,引导学生专注于核心问题去静思反省,让学生经历猜测、比较、判断、甄别、感悟等深度信息加工过程,促进思考由肤浅走向深刻,从而深入到数学灵魂深处,感知到数学思想,体悟到数学方法,培育学生的关键能力和思维品质。
在教学“分数的初步认识”的练习环节中,教师先出示平均划分好份数的长条(图4),先让学生说出其中涂色部分占这根长条的几分之一,然后出示没有显示分成几份的长条、(图5),鼓励学生猜测。在猜测时,由于受到惯性思维影响,大部分学生会认为是六分之一。这时教师采取一系列質疑追问来帮助学生建立数感:这个分数确定是六分之一吗?有没有其他可能?为什么?如果接着再往下分,就这样一直分下去,分到的数会越来越接近哪个数呢?
在图形演示和问题串的一再追问之下,学生关注于涂色部分的变化,逐渐地发现了变化的趋势,想到如果一直分下去,分到的分数会逐步变小,直至小到无限地接近0,但又不是0,这时学生就会对极限思想有一种切身的体验和感悟。这样的追问不仅激发了学生刨根问底的欲望,也激活学生的思维,让其在深度思考中领悟到数学思想方法的奥妙,在探究知识的过程中积淀了数学思想方法,培养了数学关键能力。
总之,在以培养学生核心素养为教育总目标的背景下,教师要从引发学生深度思考的角度设计和实施教学,创设具有思考价值的问题情境,去开启学生深度思考的阀门,让学生的思考在自主探索、合作交流、质疑提升的过程中逐步深入,从而想得更清晰、更全面、更深刻、更合理,有效地提升他们的关键能力和思维品质。
