杂质纵向高斯分布UTBB-SOI MOSFET的虚拟阴极阈值电压解析模型
2021-12-03韦素芬陈红霞李诗勤黄长斌
韦素芬,陈红霞,李诗勤,黄长斌,刘 璟
(1.集美大学海洋信息工程学院,福建 厦门 361021;2.瑞芯微电子股份有限公司,福建 福州 350003)
0 引言
延续摩尔定律(More Moore)仍是当今集成电路技术发展的主要方向之一[1-2]。UTBB-SOI MOSFET不但具备传统FD-SOI MOSFET电流驱动能力高、消除kink效应等诸多优点;而且相比传统FD-SOI MOSFET来说,UTBB-SOI MOSFET还有更陡峭的亚阈值斜率[3]、更出色的短沟效应抑制能力、更显著的背栅对阈值电压和电流的调控能力[4]、更强的抗辐射能力、更好的耐高温性能。因此在延续摩尔定律时代,在高速、低压低功耗纳米集成电路应用中,具备出色的发展与应用前景[5]。
阈值电压是MOS器件解析模型中的重要模型参量,对器件的直流特性、频率特性和开关特性等具有重要影响。一直以来,从传统FD-SOI器件[6-7]到UTBB-SOI器件[8],阈值电压模型一直是国内外的研究热点。目前,大多数关于UTBB-SOI MOSFET的研究都假设杂质在超薄体区均匀分布,然而无论是对于长沟重掺杂的器件,还是短沟轻掺杂或极轻掺杂的器件,这样的假设与实际工艺步骤之后产生的器件杂质分布特性都不相吻合,尤其是对于体区轻掺杂的UTBB-SOI器件而言,减少掺杂浓度的目的不仅是为了提高迁移率,也是为了尽量减小掺杂浓度不均匀对于器件电特性的影响。但,即使掺杂浓度降低到了1014~1015cm-3数量级,掺杂浓度的轻微不均匀特性仍会对纳米器件特性产生不可忽略的影响[9]。沟道非均匀掺杂对器件特性的影响随着尺寸的缩小而更显著。因此,研究体区杂质非均匀掺杂对器件阈值电压的影响有着重要的实际意义。
1 纵向离子注入及快速热退火与高斯函数的对比

n沟UTBB-SOI MOSFET器件结构如图1所示。x轴方向为沿源/沟道界面的垂直方向,y轴方向为沿栅-栅氧化层界面的水平方向;toxf、tsi、toxb、tsub、xd_sub是栅氧层、硅膜、埋氧层、衬底的厚度及衬底内耗尽层深度;L为沟道长度;NSD为源漏区掺杂浓度,NB(x)为硅膜掺杂浓度,NSub为衬底掺杂浓度;VD、VS、VG、VSub分别为漏、源、栅、衬底偏置电压;器件的源端接地。在模拟时假设:n+型源漏区杂质呈均匀分布,p型衬底杂质呈均匀分布,轻掺杂p型硅膜内杂质呈横向(y轴方向)均匀分布。
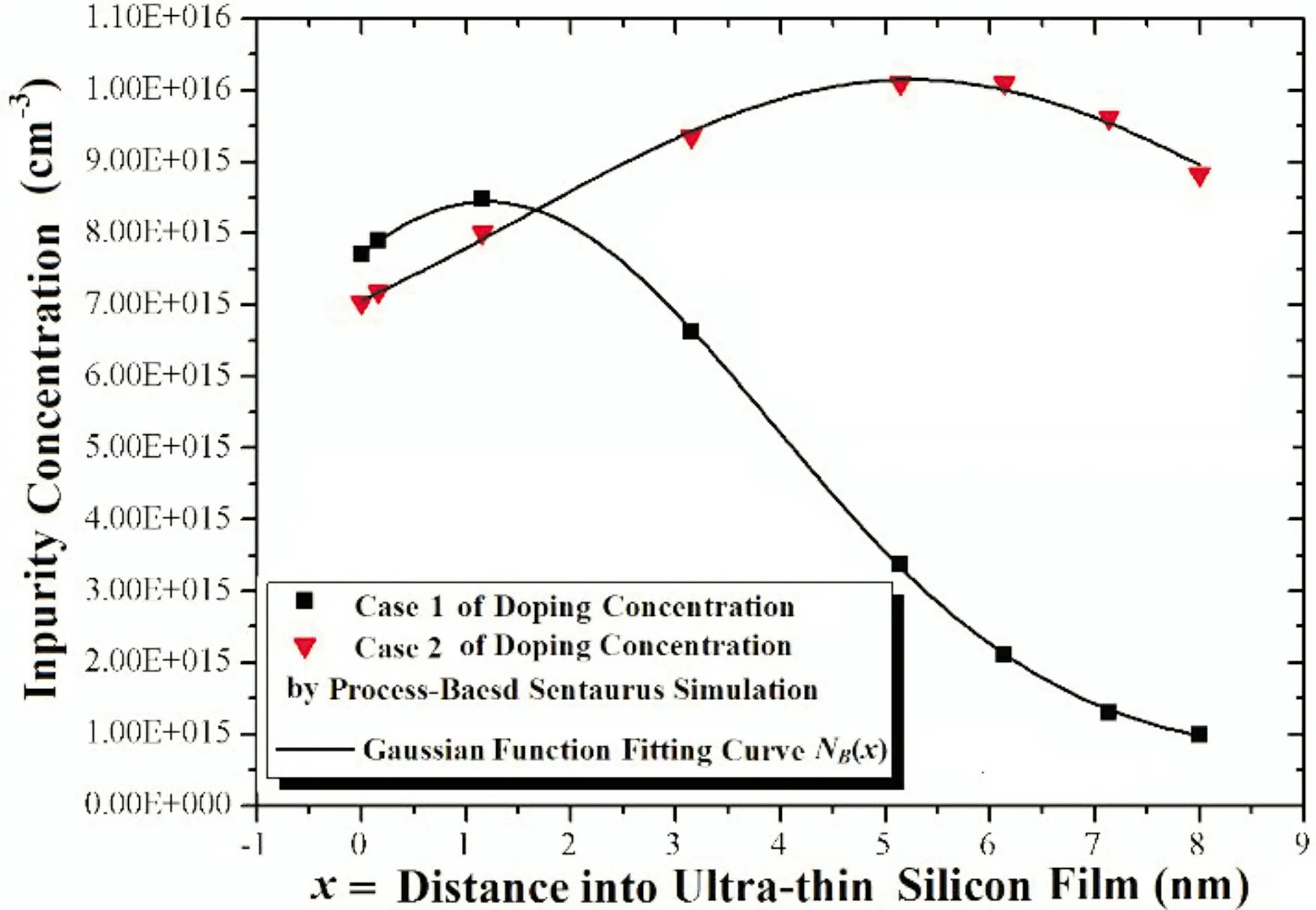
本研究的UTBB-SOI MOSFET的超薄硅膜基于智能剥离(smart-cut)技术形成。将器件厚度定为:tsi为8~25 nm;toxb为10~30 nm;toxf为1~3 nm。p型衬底掺杂浓度为1×1017cm-3,源区与漏区掺杂浓度为2×1020cm-3。对UTBB-SOI MOSFET来说,硅膜通常采用轻掺杂。为使得轻掺杂UTBB-SOI MOSFET的p型硅膜内的杂质分布与实际工艺相符,基于实际轻掺杂时硼注入的剂量和能量,先进行纵向无晶圆自转的硼离子注入,后继一次快速热退火。使用工艺模拟软件Sentaurus Process对以上工艺步骤进行模拟,对所形成器件硅膜内的杂质纵向分布规律进行曲线化拟合和分析。工艺模拟与曲线拟合结果分别如图2所示。
在工艺仿真分析UTBB-SOI MOSFET的掺杂特性变化时,固定栅氧与埋氧厚度:toxf=2 nm,toxb=30 nm;改变硅膜厚度:tsi=8 nm,tsi=25 nm。针对这两种不同硅膜厚度,分别调整硼注入的剂量和能量,进行四次纵向离子注入,以产生不同的掺杂分布特性,硅膜内的平均掺杂浓度保持在1014~1015cm-3数量级。每次离子注入均有后继一次2 s的快速热退火。在图2中,离散点为工艺仿真软件Sentaurus Process所计算出的纵向杂质分布点,实线为对应离散点图形采用Origin工具所拟合的高斯函数NB(x),其表达式为:
NB(x)=Np·exp[-((x-R)/σ)2/2](toxf≤x≤toxf+tsi)。
(1)
其中:R为高斯函数平均投影射程(nm);Np为高斯函数峰值(cm-3);σ为高斯函数标准差(nm)。从图2可看出:采用垂直于沟道方向无晶圆自转的一次离子注入,之后再配合一次快速热退火,在硅膜内所形成的杂质在水平方向呈均匀分布,在垂直方向分布规律与高斯函数一致。因此,在本文的仿真和分析中,采用式(1)的高斯函数NB(x)表征轻掺杂硅膜内的杂质分布。
2 基于虚拟阴极的阈值电压的定义与推导
2.1 基于虚拟阴极的阈值电压的定义
对短沟道轻掺杂、极轻掺杂和非掺杂UTBB-SOI MOSFET,阈值电压定义不再基于长沟重掺杂器件阈值电压关系式中加入修正项,而是引入虚拟阴极的概念来定义阈值电压。虚拟阴极是指正、背栅电压作用下硅膜内电势最小值所在的位置。在杂质纵向非均匀分布的情况下,虚拟阴极位置并不一定位于硅膜的正、背表面,而是有可能位于硅膜的内部[10-11]。
对于纳米轻掺杂UTBB-SOI MOSFET,由沟道表面势最小值等于两倍体费米势得到阈值电压的计算方法被认为不再准确[12-13]。为定义短沟轻掺杂器件阈值电压,引入虚拟阴极的概念。Fasarakis[8]提出:以衡量内部虚拟阴极点反型载流子浓度来定义阈值电压。当虚拟阴极(即:电势最小值处)的反型载流子浓度等于衬底深处掺杂平坦处多数载流子数目时,这时的栅源电压称为阈值电压。但是硅膜内部虚拟阴极准确位置的计算过程极其复杂,在阈值电压模型建立过程中若采用求解硅膜内部虚拟阴极点的电势值(即:反型载流子浓度大小)来判断是否达到阈值电压,其工程应用性会受很大局限。

2.2 基于虚拟阴极的阈值电压的推导
硅膜内电势最小值所在的位置称为“虚拟阴极”。在本研究中用到了两个虚拟阴极的概念。一个是基于文献[14-15]的近似:假设正、背栅电压分别对应的虚拟阴极就位于正、背表面,称为“表面虚拟阴极”,即正、背表面电势最小值所在位置;另一个是指Fasarakis等[8]与Karatsori等[16]提出的将位于硅膜内部的电势最小值的位置称为“内部虚拟阴极”。在本文阈值电压模型推导中使用了“表面虚拟阴极”和“内部虚拟阴极”这两个概念,并采用“表面虚拟阴极”的y坐标近似地表征“内部虚拟阴极”的y坐标。对于轻掺杂硅膜内杂质纵向高斯分布的UTBB-SOI MOSFET,其正、背栅控制的二维电势分布函数模型φ(x,y)采用Wei等[17]所提出的基于分离变量求解得到的硅膜内的二维电势分布函数的表达式。定义(taxf,ymin_SF)为正表面虚拟阴极坐标, (taxf+tsi,ymin_SB)为背表面虚拟阴极坐标。正、背表面虚拟阴极的y坐标可通过分别将正、背表面势函数对y求导数得到。


(2)

(3)
根据基于虚拟阴极的电荷面密度法阈值电压的定义,还需要衬底深处掺杂平坦处多数载流子电荷面密度QTH。本研究中器件的衬底为超薄硅膜,在硅膜纵向掺杂不平坦,遵循高斯分布NB(x)。因此,以基于高斯函数纵向均值的平均掺杂浓度来计算QTH:
(4)

(5)
(6)
正、背栅控制的杂质纵向高斯分布的UTBB-SOI MOSFET的阈值电压VTH为:
VTH=min(VTHF,VTHB)。
(7)
3 阈值电压的仿真验证
阈值电压是由器件参数决定的,反映杂质纵向高斯分布的非均匀掺杂UTBB-SOI MOSFET各器件参数对阈值电压的影响趋势,并可验证模型的正确性。本研究利用式(7)所求得的阈值解析模型,对不同的器件参数Np、R、σ、toxf、tsi、toxb以及不同VSub条件下,阈值电压随沟道长度的变化关系进行了计算与分析;还就不同沟道长度下,阈值电压随VSub的变化关系进行了计算与分析;接着,利用器件数值仿真软件Sentaurus Device进行数值模拟,基于数值仿真得出的器件转移特性曲线,采用最大跨导法提取器件的阈值电压,对比模型所得阈值,进行分析和验证。
在阈值电压的器件仿真过程中所分析的器件是UTBB结构,仿真所采用的物理学模型为:载流子的输运模型采用“Drift-Diffusion”模型;载流子的掺杂采用“Fermi-Dirac” 模型;载流子的产生-复合采用 “SRH and Auger Recombination Models”; 载流子的迁移率采用“Enormal Mobility Model”;仿真中计入的禁带宽度变窄效应“band-gap narrowing effects”;通过设置MLDA 选项,考虑了体区的界面态效应。应强调的是:本研究中器件沟道长度的范围为22~100 nm。由于沟道长度大于22 nm,故在阈值电压模型中未引入量子效应修正项。
图3~8的分析中,VDS=0.05 V,VSub=0 V。图3~5给出在不同的栅氧层厚度、硅膜厚度、埋氧层厚度情况下,阈值电压随沟道长度变化曲线的改变趋势。杂质纵向高斯分布函数的峰值Np=9.48×1014cm-3,平均投影射程R=15.75 nm,标准差σ=4.62 nm。

图3给出toxf改变时阈值电压随沟道长度变化的关系曲线。在改变toxf时,固定tsi=15 nm、toxb=20 nm。从图3可以看出:1)在同一个沟道长度节点上,阈值电压随着栅氧层厚度的减小而相应减小。2)不论toxf为何值,当沟道长度减少时阈值电压都减少。相较而言,当栅氧层相对较薄的时候,阈值电压随沟道长度减小而减小的趋势更加急剧;当栅氧层变得略厚时,若沟道长度变短,阈值电压减小的趋势会变得缓慢一些。这是因为更薄的栅氧化层对于沟道电荷的控制能力更强,对阈值电压的调控更灵敏。正是由于这个原因,当沟道长度变短时,UTBB-SOI MOSFET工艺的栅氧层也会比较薄。
图4为硅膜厚度的改变对于阈值电压随沟道长度变化特性的影响。在改变tsi时,固定toxf=2 nm、toxb=20 nm。在同一个沟道长度的节点上,阈值电压随着硅膜厚度的增大而减少。因此,硅膜厚度减小相当于减小体硅器件的结深,对于短沟效应的抑制效果就越佳,这正是将体区减薄的主要原因。
图5为埋氧层厚度的改变对于阈值电压随沟道长度改变特性的影响。改变toxb时,固定toxf=2 nm、tsi=15 nm。由图5可见:阈值电压随着埋氧层厚度的减少而增大;而且,埋氧层的厚度越薄,在纳米沟道的范围内,阈值电压随沟道长度的减少而减少的趋势相对越平缓。由此可以看出,减薄埋氧层的厚度,可以在一定程度上减少源、漏与衬底之间的耦合[15-16],因此可以更好地抑制短沟效应。这也是将埋氧区减薄的原因。


图6~8给出了当杂质纵向高斯掺杂特性改变时,阈值电压随沟道长度变化曲线的改变趋势。固定toxf=2 nm,tsi=15 nm,toxb=20 nm。图6为在不同高斯峰值的条件下,阈值电压随沟道长度而改变的特性曲线的变化趋势。在改变Np时,固定R=15.75 nm,σ=4.62 nm。由图6可看出:1) 高斯峰值越大,沟道中杂质整体掺杂浓度越大,因此,在各沟道长度节点上阈值电压值也就相应地越大,在这一点上和杂质均匀分布时一致;2)随峰值增加,整体掺杂浓度增加,阈值电压漂移(threshold roll-off)会略微减缓。
图7为在不同的高斯平均投影射程的情况下,阈值电压随沟道长度而改变的特性曲线的变化趋势。在改变高斯分布函数的平均投影射程时,固定Np=9.48×1014cm-3、σ=4.62 nm。当R越接近硅膜纵向的中心(tsi/2)时,硅膜内整体的掺杂浓度越高,阈值电压越大。当R>(tsi/2)时,高斯分布函数的峰值会更接近硅膜的背表面,这使得硅膜正表面至硅膜中心线的整个硅膜上半部分的平均掺杂浓度比硅膜下半部分的平均掺杂浓度低,造成硅膜正表面阈值电压小于背表面阈值电压(VTHF
与上面相类似的情况还体现在高斯标准差σ的改变对于阈值电压随沟道长度变化的影响上,图8展示了在不同高斯标准差的条件下,阈值电压随沟道长度而改变其特性曲线的变化趋势。在改变σ时,固定Np=9.48×1014cm-3,R=15.75 nm。当σ增大时,硅膜内每一个位置的掺杂浓度都会减少(除了峰值浓度固定不变以外),即沟道中杂质的整体掺杂浓度减少,因此,在各个沟道长度节点上阈值电压值也就相应地增大,在这一点上和杂质均匀分布的特性仍是一致的。
图9~10分析衬源偏压对于阈值电压的影响。其中,VDS=0.05 V,Np=9.48×1014cm-3,R=15.75 nm,σ=4.62 nm,toxf=2 nm,tsi=18 nm,toxb=20 nm。图9对比了不同的VGS与VSub偏电对于阈值电压随沟道长度改变的趋势。当VGS=0.8 V,VSub=0 V时,硅膜正表面率先形成反型沟道,正表面阈值电压是器件的阈值电压;当VGS=0.8 V,VSub=1.5 V时,硅膜背表面率先形成反型沟道,背表面阈值电压是器件的阈值电压。

由图9可见,器件在不同正、背栅压的控制之下,阈值电压值变化很大。因此,由于埋氧层厚度的减薄,UTBB-SOI MOSFET可利用调整背栅压的方式实现对阈值电压动态、有效的调制。
图10展示了当器件沟道长度L分别为22 nm、40 nm、70 nm时,阈值电压随衬源偏压VSub而改变的曲线。可看出:无论沟道长度等于22 nm、40 nm,还是70 nm,随着VSub从-7 V增大到+1 V,阈值电压都呈现出线性减小的关系,而且三种沟道器件的曲线的线性度都比较好;随着沟道长度减少,曲线的线性度会略微变差一点。这说明在VSub的影响下,硅膜的背界面形成反型沟道时,影响背沟道的短沟效应不是很明显。
由图3~10可得出结论:在改变杂质纵向分布高斯函数特性、改变器件厚度、改变衬源偏压的情况下,基于“虚拟阴极的电荷面密度法”对于阈值电压的定义,推导得出的阈值电压模型计算值与Sentaurus Device器件模拟值基本吻合。
4 结论
首先,基于形成轻掺杂超薄体的实际硼注入剂量和能量,利用工艺仿真工具,验证了纵向离子注入后经快速热退火所得到的杂质分布符合高斯函数特性。然后,针对杂质纵向高斯分布的UTBB-SOI MOSFET,采用“虚拟阴极的电荷面密度法”对于阈值电压的定义,对超薄硅膜内杂质纵向高斯分布的UTBB-SOI MOSFET,推导出阈值电压解析模型。利用该模型计算了不同器件参数(高斯掺杂平均投影射程、高斯标准差、高斯掺杂峰值浓度、栅氧厚度、硅膜厚度、埋氧厚度),以及在不同的衬源偏压的条件下,器件阈值电压随沟道长度的变化关系。最后,分析在不同的沟道长度下,器件阈值电压随衬源偏压的变化关系,模型计算值与Sentaurus Device数值仿真有良好的一致性。
本文所研究的硅膜内杂质纵向高斯分布是基于现行实际工艺步骤得到的真实分布规律。基于高斯分布推导出的阈值电压模型公式,不但具备工程应用实际意义,而且求解模型的方法可以进一步应用到硅膜内具有更复杂掺杂特性的UTBB-SOI MOSFET器件上;更重要的是,在阈值电压的计算中融入了杂质高斯分布的影响,考虑高斯分布对于器件“虚拟阴极”位置的影响,在求解虚拟阴极的位置时,采取了合理的近似。这样既保证了模型的准确性,又兼顾了模型的工程实用性。
