阈值引导采样法的船舶轨迹简化算法

2021-12-03张银昊潘家财赵梦鸽

集美大学学报（自然科学版） 2021年5期

张银昊，潘家财,赵梦鸽

(集美大学航海学院，福建厦门 361021)

0 引言

船舶AIS(automatic identification system)数据蕴含丰富的船舶信息，利用这些数据能够发现和分析船舶的行为，从而为海事部门对船舶航行的安全监管和决策提供支持服务[1-2]。船舶AIS数据具有量大、实时、多样等特征，准确地存储和提取这些数据是分析船舶轨迹的前提，但是海量的数据会使查询和计算效率降低，因此，通常需要采用轨迹简化的方法来处理轨迹数据，进而保留关键数据点，减少轨迹数据存储的负担。目前，国内外学者对船舶轨迹简化进行了许多研究。文献[3]提出了使用垂直欧式距离(perpendicular euclidean distance)进行轨迹简化；时间同步欧式距离(time synchronized euclidian distance)[4]是基于时间同步的轨迹计算方式来产生近似轨迹。Zhao[5]基于douglas-peucker模型[6]建立轨迹点批处理模式,但在实际的轨迹简化处理中,很难实现批处理模式，该研究仅仅衡量了船舶的经纬度的位置信息，忽视了航速和航向信息。潘家财[7]根据船舶航行的特征，对航向和航速变化率设置阈值进行特征点的选取；而肖潇[8]利用最小描述长度准则[9](minimum description length，MDL)进一步在航速、航向变化率之上筛选特征点，但是该方法缺少对AIS信息多因素的综合考虑。角度阈值法[10]是一种以轨迹点的角度变化作为衡量标准的轨迹简化方法，计算每一个轨迹点的角度变化量，若大于阈值，当前轨迹点视为特征点。

轨迹简化主要运用于轨迹聚类，轨迹聚类主要分为两种：1)将船舶的轨迹视为整体进行聚类[11]；2)将船舶轨迹进行分段，分别对分段后的轨迹子段进行聚类分析，将相似的轨迹子段归类为簇，保证轨迹运动的细节信息不丢失[12-15]。目前，对两种简化方式均能兼顾的轨迹简化方法较少。

本文根据船舶移动轨迹的运动特征，在角度阈值法[10]的基础上提出一种新的轨迹简化方法——阈值引导采样法，并采用聚类实验方法进行验证。实验结果表明，该方法在轨迹段聚类和整体轨迹聚类的应用上均有较好的聚类效果。

1 阈值引导采样算法

1.1 相关理论

阈值引导采样法是在角度阈值法[10]的基础上提出的一种新的简化方法。角度阈值法[10]通过设置角度的阈值，并将当前点与上一个点之间的角度进行对比，角度差大于阈值时，当前轨迹点视为特征点。阈值引导采样法沿用了角度特征判断的特点，设置了船舶转向角变化的角度阈值θmax，进行角度特征的判定；同时，还增设了速度阈值Smax，以及方位角阈值βmax，从船舶速度及转角两个方面对船舶轨道特征点做进一步判断。

船舶数据出现时间位置不合理的情况主要为：在较大时间区间内反复进出研究水域的边界；在较大时间段内突然丢失船舶的轨迹数据；仅有一个数据点的船舶。为解决这个问题，设置了中断特征点(Interrupted feature point)，为了判断中断特征点，对轨迹设置了时间间隔阈值tmax，准确地分割轨迹。

1.2 参数定义

1.2.1 初始轨迹信息

原始轨迹Ti={p1,…,pj,…,pn}，pj=(i,sj,cj,tj,lonj,latj)，其中：Ti是船舶为i的轨迹数据点集合；pj为轨迹i的第j个轨迹点；sj为轨迹点j的SOG(speed over ground)；cj为轨迹点j的COG(course over ground)；tj为轨迹点j的时刻；lonj和latj分别表示轨迹点j的经度和纬度。

简化后的轨迹信息：Tmsimp={pmsimp_1,pmsimp_2,…,pmsimp_k,…,pmsimp_d}，pmsimp_k表示Ti中的特征点。

1.2.2 角度阈值和速度阈值

对于Ti中的轨迹点pj，满足Cdiff≥θmax，则pj视为角度特征点。其中：角度差Cdiff=|cj-1-cj|；θmax为角度阈值。

对于Ti中的轨迹点pj，满足Sdiff≥Smax，则pj视为速度特征点。其中：速度差Sdiff=|sj-1-sj|；Smax为速度阈值。

通常角度阈值和速度阈值需要根据研究对象的运动习惯来确定。例如，船舶的极限舵角通常为30°～35°，航行时船舶改变航向次数往往多于改变航速次数。因此，角度阈值一般设置为0°～5°，若为了追求更简洁的简化轨迹，可将角度阈值设为15°，而速度阈值一般在0～3 kn内选取。

1.2.3 中断特征点

对于Ti中的轨迹点pj，满足tdiff≥tmax，则pj视为中断特征点，pj=pmsimp_d，pj+1=pm+1simp_1。其中：时间差tdiff=|tj-1-tj|；tmax为时间间隔阈值。选取A级船长230 m以上船舶的AIS数据，该类船舶自主模式下信息更新率最大为180 s[16]。中断特征点以时间差为阈值进行判断，再考虑误差，tmax一般选取为180～300 s。

1.2.4 方位角阈值

对于Ti中的轨迹点pj，满足βdiff≥βmax，则pj视为方位角特征点。其中：βmax为方位角阈值，轨迹线段的坐标方位角差为aziij=|ci-cj|，方位角差βdiff=|azii(i+1)-aziij|，ci为pj的上一个特征点的COG，cj为pj的COG。通常方位角阈值的大小需要根据研究水域的转向点的角度来确定，例如，当转向点处两航道的夹角为20°时，为了保留一定的空间，方位角阈值设置需要在夹角基础上增加约10°，即方位角阈值设为30°，然后在这个阈值附近进行调整，进行多次的实验，选取更精确的阈值。

1.3 轨迹点特征优先级的判断

在轨迹简化过程中，为避免数据点出现的时间位置不合理而被视为一条轨迹的情况，应优先判断数据点是否为中断特征点，将轨迹进行分割。在船舶轨迹分析中，船位的突变必然导致航速或航向的异常，但船速和航向的突变未必会带来船位的异常。根据信息熵理论[17]，船位异常事件所携带的信息大于航速与航向异常事件的信息量，在判断优先级上优先判断信息量较大的属性，能减少运算量，提高运算效率。因此，需要优先判断数据点的方位角特征，再判断角度与速度特征。

轨迹点特征判断具体如下：

1)判断点的方向和速度位于上一个点的方向和速度的阈值区间内，则该点视为可简化。如图1所示，O、A、B、C、D为一条船舶的5个AIS轨迹点，按照时序排列；Vmin为上一个点的SOG；Vmax=Vmin+Smax；2θmax的中分线方向为上一个点的COG；FX表示船舶在点X的COG。由于O、D两点为起点与终点，无需判断，均视为特征点。从第二个点A开始判断是否属于特征点，FA的长度为船舶在A点的SOG，当F的长度没有落在(Vmin,Vmax)内时，A点因速度变化过大而视为轨迹的特征点；同理，FA的方向没有落在2θmax范围内，则A点因角度变化过大而视为轨迹的特征点。因此，当判断点不满足以上任意一个条件，就将该点视为轨迹特征点。同理，下一个待判断点B，将上一个点A的SOG视为Vmin，点A的COG视为2θmax的中分线方向。以此类推，直至轨迹的倒数第二个点，简化完全部轨迹点。

2)方位角的特征判断如图2所示。其中，TOE和TOA为轨迹OE和OA的线方位角，点A、B、C、D均满足角度和速度阈值的传递要求，由于|TOE-TOA|>βmax，表明从D点之后所有点超过方位角阈值，因此，将超过方位角阈值E点的上一个点D视为轨迹的方位角特征点，最终简化轨迹为ODE，即OD段和DE段轨迹；当2βmax=360°时，不设置方位角阈值，此时算法为整体轨迹的简化；当2βmax<360°时，算法存在方位角阈值判定，为分段轨迹的简化。

1.4 阈值引导采样法算法流程图

算法流程如图3所示。首先输入一条轨迹的特征点集，对数据点进行中断特征点的判定，将轨迹进行分割；其次，对数据点进行方位角特征判定，对轨迹进行分段；最后，通过判断角度与速度特征进行子轨迹的简化。

1.5 阈值引导采样法的伪代码

输入原始轨迹T={T1,…,Ti,…,TN}，Ti={p1,…,pj,…,pn}，pj=(i,sj,cj,tj,lonj,latj)；输入速度阈值Smax、角度阈值θmax、方位角阈值βmax、时间间隔阈值tmax。简化后的轨迹段集合为：Lsimp={Psimp_1,…,Psimp_m,…,Psimp_k},(1≤m≤k)。其中简化的轨迹段Psimp_m(pmstart,pmdown)元素pmstart和pmdown分别为轨迹点集简化后选取的特征点的起点和终点。

基于阈值引导采样法的船舶轨迹简化算法如下：

1)输入：原始轨迹T，参数Smax、θmax、βmax、tmax，

2)foriinN，

3) forjinn:

5) iftdiff>tmax:

6)pj-1=pmdown,m=m+1，pj=pmstart，

7) continue，

8) Else if |aziii+1-aziij|>βmax:

9)pmdown=pj-1，m=m+1，pmstart=pj-1，

10) ElseCdiff>θmaxorSdiff>Smax:

11)pmdown=pj-1，m=m+1，pmstart=pj-1，

12)输出：轨迹段集合Lsimp。

2 实验结果分析

本文选取了两组实验数据与角度阈值法进行对比分析，为了避免误差分析的不准确，轨迹的预处理条件均相同，采用的验证聚类算法为DBSCAN[18]，轨迹相似性度量的方法选择为Hausdorff距离[17]。其中，DBSCAN的参数Eps(领域距离阈值)和MinPts(密度阈值)为反复多次实验选取。实验所有涉及距离和方位角信息均以WGS84为坐标进行计算。

第一组轨迹简化和聚类实验，选取了厦门港2012年1月1日全天的AIS数据，一共有88条船舶，3 650个数据点。水域范围选取24.340°N～24.450°N，118.130°E～118.167°E；方位角阈值参数βmax=180°;时间间隔阈值tmax=180 s，180 s为AIS信息播发的最大间隔。同时为了使初始数据具有可操作性与真实性，删除了以下几种情况的AIS数据：MMSI≤100000000；0°>COG；COG>360°；SOG>50 kn；SOG<0 kn。

第二组简化分段聚类实验，选取了厦门港2016年1月1日至2016年1月13日的10 000条船舶的AIS数据点，水域范围选取24.350°N～24.600°N，117.900°E～118.150°E，船舶类型选取船长大于230 m的货船。各参数值为：时间间隔阈值为180 s;方位角阈值设置为15°；因船舶的移动特性，将角度阈值设置为10°;速度阈值设置为3 kn；因厦门港航道宽度约为300 m，经反复实验将DBSCAN的Eps设置为230 m，MinPts为5。

第三组实验与第二组实验数据水域范围相同，选取2016年2月1日至2016年2月9日的20 000条AIS数据点，船舶类型不做限定，船长选择大于20 m。各参数取值为：时间间隔阈值为180 s；方位角阈值为20°；因船舶的移动特性，将角度阈值设置为10°；速度阈值为3 kn；经反复实验将DBSCAN的Eps设置为600 m，MinPts为5。

2.1 简化率和误差定义

定义1：设轨迹简化率η为剩余简化轨迹点的数量n-pa_b与原始轨迹点数量n之间的比值，即η=(n-pa_b)/n。其中：pa_b表示角度阈值为a，速度阈值为b时的简化轨迹点数量；n≥2，且n≥pa_b。

定义2：设简化效率μ为A方法轨迹简化率ηA与B方法轨迹简化率ηB的比值，即μ=ηA/ηB。

定义3：设简化误差率δ为A方法简化后剩余轨迹与B方法简化后剩余轨迹之差与原始轨迹点数之间的比值，即δ=(pA-pB)/n。

2.2 轨迹简化实验结果分析

用第一组实验数据分析船舶轨迹简化结果。原始轨迹如图4所示，该水域包括两条航道和一个锚泊水域，其中位于水域最顶部较多曲折轨迹为锚泊水域，中间与下半部分的轨迹集为两条航道。

采用控制变量法对各参数的简化效率进行分析,简化后剩余的轨迹点实验结果如图5所示。

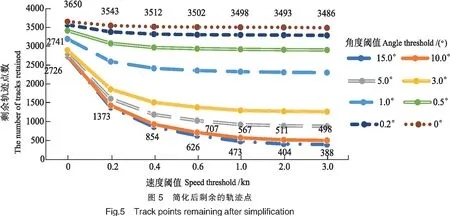
在进行中断特征点的判定后，Smax=0时的阈值引导采样法，即为Long[10]提出的角度阈值法。采用阈值引导采样法分别对角度阈值的变化以及速度阈值的变化进行实验，简化结果可知：当角度阈值固定时，随着速度阈值的增大，每一条折线的纵坐标依次递减，数据减少，简化效率提高；当速度阈值固定，随着角度阈值的增大，每一列(相同速度的不同角度阈值视为一列)的纵坐标依次递减，数据减少，简化效率提高。可见本算法比角度阈值法有了较大提升。例如：实验中选取角度阈值法进行简化，15°角度阈值时，简化率最高为：η=(n-p15_0)/n=(3650-2726)/3650=25.31%。

以阈值引导采样法进行轨迹简化，当角度阈值为15°，速度阈值为3 kn，轨迹简化率η=(n-p15_3)/n=(3650-338)/3650=90.73%;简化效率μ=η15_3/η15_0=90.71%/25.31%≈3.6。

即阈值引导采样法的简化效率是角度阈值法的3.6倍。同理，当以速度阈值不变，角度阈值变化的情况下，随着角度阈值增大，简化效率也增大，简化剩余的轨迹数越少。

简化效率并非越高越好，而是应该在尽可能保留特征属性的情况下进行高效的简化。在角度阈值为0°，速度阈值为2 kn与3 kn的条件下，简化结果表明，仅存在7个数据点的相邻速度变化超过了2 kn，即速度特征点为7个；角度阈值为15°，速度阈值为2 kn与3 kn的条件下，简化结果表明，存在16个数据点的相邻速度变化超过了2 kn，即多识别出9个角度特征点。因此相比角度阈值法，阈值引导采样法的简化误差率δ=[(p15_2-p15_3)-(p0_2-p0_3)]/n=[(404-388)-(3493-3486)]/3650=2.47‰。

以上分析表明，经过处理后的数据依旧具有较好的特征点识别率，能极大地保留原始轨迹的形状与特征点。

2.3 轨迹简化算法的聚类实验

在轨迹简化的应用方面，阈值引导采样法不仅有较好的聚类效果，而且能精准地识别角度阈值法不能识别的异常轨迹。

第一组实验的轨迹聚类结果如图6所示。轨迹集一共分为三个簇(cluster)，代表了3条习惯航路的轨迹，航迹A和航迹B被标记为异常轨道。其中：航迹A横穿中间航道，该部分原始轨迹局部放大后如图7所示；航迹B处于中间航道和下侧航道中间，阈值引导采样法的轨迹聚类结果如图8所示。除了3条习惯航路的轨迹被准确识别外，横穿航道的航迹A以及部分航行数据异常的轨迹也被识别出，横穿航道的航迹A被进行了准确分割，局面放大后如图9所示。

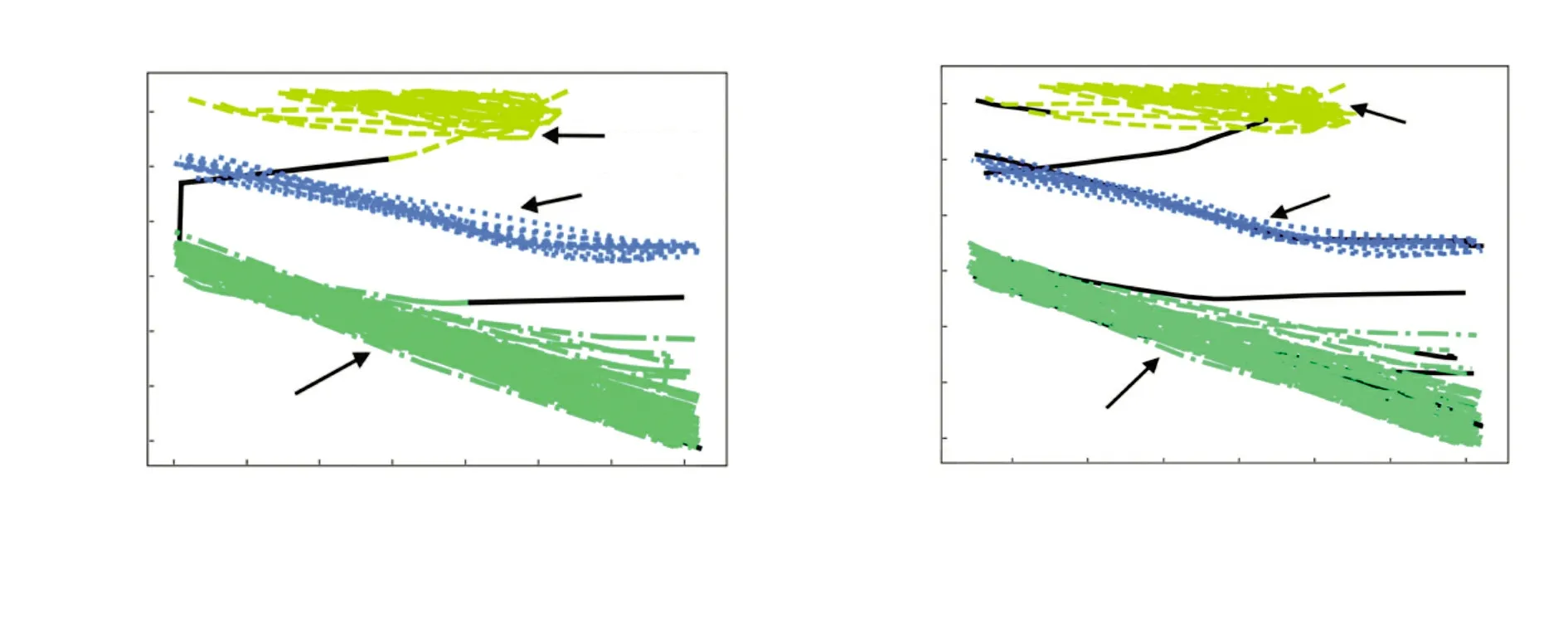
综上可知：对比角度阈值法，本算法不仅能完全识别横穿航道的轨迹，而且可以对时间间隔过大的轨迹进行分割，避免了反复进出研究水域的相同MMSI的轨迹点被视为同一时序中的序列，提高了数据的质量。

第二组实验在区域较大且环境复杂的港口水域进行。该实验不同于整体聚类，需要将轨迹先进行分段简化再聚类。由于主航道至海沧航道的转向较小，因此从海沧航道至主航道的来往船舶轨迹视为一类；而东渡航道至主航道往来船舶在Y型分叉口有极大的转向，因此视为两类船舶轨迹，一类为东渡航道至主航道往来船舶截至Y型分叉口的轨迹，一类为主航道至东渡航道来往船舶截至Y型分叉口的轨迹。

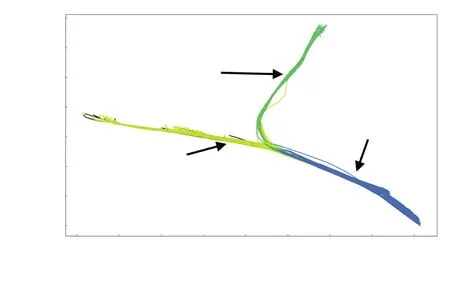
实验的聚类结果如图10所示。其中：簇1为从海沧航道至主航道的船舶来往轨迹；簇2即为东渡航道至主航道往来船舶截至Y型分叉口的轨迹；簇3为主航道至东渡航道来往船舶截至Y型分叉口的轨迹。

实验结果表明：本文提出的轨迹简化算法对原始轨迹进行简化后，其简化的轨迹能应用于轨迹聚类，能分段聚类出较大转向的船舶轨迹。

第三组实验数据为船长20 m以上的船舶在厦门港的聚类，此时船舶轨迹出现在招银航道、厦鼓航道，tmax=180 s，Smax=3kn，θmax=10°，βmax=20°，船舶的轨迹点的数量由20 000简化至3930，简化率η=(n-p10_3)/n=(20 000-3930)/20 000=80.35%，轨迹简化效果较为理想。

实验的聚类结果如图11所示。其中：簇1为主航道至招银航道的船舶往来轨迹；簇2为海沧航道至主航道的船舶来往轨迹；簇3为东渡航道的船舶轨迹；簇4为主航道至厦鼓航道的船舶往来轨迹；簇5位为东渡航道至主航道往来船舶截至Y型分叉口的轨迹。

实验结果表明：在频繁变向的船舶轨迹数据中，本文提出的简化算法简化率良好，将简化的轨迹数据进行聚类实验，聚类效果较为理想。