基于Bi-BPNNs的船舶轨迹修复模型

李 樾，袁 智,，刘 奕

(1.湖北工程学院新技术学院，湖北 孝感 432000； 2.武汉理工大学航运学院，湖北 武汉 430063)

0 引言

日益繁忙的水上交通给船舶交通监管和事故预防带来了巨大压力[1]。船舶轨迹数据因为记录了船舶航行过程中的实时位置和航线信息，从而为水上船舶轨迹分析、交通流分析、船舶交通监管和水上事故预防提供了重要的信息[2]。区域内船舶基于GPS(global positioning system)、AIS(automatic identification system)设备不断地与他船和岸基以报文的形式发送和接收船舶数据，这些数据包括船舶的静态特征、实时位置、速度、航线以及其他信息。但是，由于受采集设备、信号传输以及环境等因素的影响，原始采样的轨迹数据存在异常和错误等质量问题[3]，从而造成船舶轨迹数据异常和部分缺失。因此，有必要构建船舶轨迹修复模型来提升船舶轨迹数据的质量，从而提高轨迹数据的利用效率和研究价值。针对船舶轨迹修复的研究，国内外学者已经取得了一些成果。刘立群等[4]通过三次样条插值法分别对船舶经度、纬度信息进行修复。秦红星等[5]以线性插值为基础，提出了一种船舶轨迹修复算法。李佳等[6]利用粒子群优化算法和相似轨迹优化最小二乘支持向量机模型修复残缺轨迹数据。Liu等[7]基于支持向量机方法构建了船舶轨迹预测模型。Lv[8]借助大数据和云计算技术对船舶轨迹进行了分析。现有这些方法多基于线性插值方法，不能很好地把握整体轨迹的特征，尤其不能很好地处理弯曲航段的轨迹。将船舶轨迹数据看作有序的时间序列，通过分析异常或缺失轨迹的上下文信息，构建轨迹修复模型，可以实现船舶轨迹的修复。与传统的线性插值方法相比，神经网络在轨迹预测建模方面有明显的优势，可以根据原始轨迹数据的上下文信息双向学习整个船舶轨迹的变化规律，从而保证轨迹修复的精度。BP(back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，有很强的非线性逼近功能，在数据分析和预测方面有着广泛的应用[9]。

本文对船舶原始轨迹数据进行分析，引入BP神经网络方法，构建Bi-BPNNs预测模型，从前后两个方向对异常或缺失的船舶轨迹进行循环修复，从而解决船舶轨迹数据丢失问题。在此基础上，基于采集的真实船舶轨迹数据进行实例研究，并与基础BP网络模型和常用线性插值方法进行对比分析，从而验证本文提出模型的有效性和实用性。

1 基于BP神经网络的船舶轨迹双向修复模型

船舶轨迹可看作是船舶航行时间和当前位置构成的序列，相邻的轨迹点之间有一定的联系。基于BP神经网络构建轨迹修复模型，可以学习历史轨迹序列之间的变化特征来预测未来时间的轨迹，从而实现缺失轨迹的修复[10]。

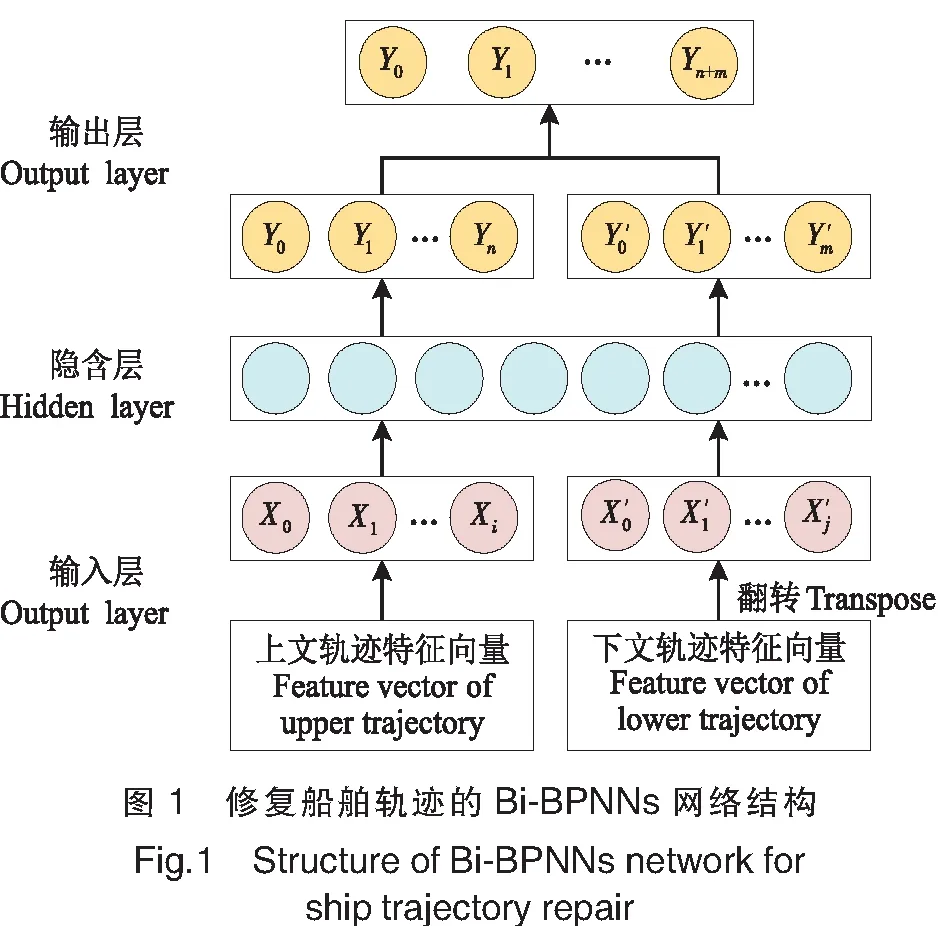
BP神经网络有三个要素：网络拓扑结构、传递函数和学习算法。一个简单BP神经网络的拓扑结构包括输入层、隐含层和输出层。其中，隐含层又有单隐含层和多隐含层结构，隐含层越多，网络越复杂，学习的能力也越强，但是训练的时间过长，会导致模型过拟合。BP网络的传递函数是非线性变换函数Sigmoid函数，其特点是函数本身及其导数都是连续的。BP神经网络的学习算法为δ算法，输入层、隐含层和输出层的权值调整公式均由学习率、误差信号和输入信号三个因素决定，输入层误差信号直接反应了网络的输出误差，隐含层的误差信号从输出层开始逐层反传过来得到。

船舶轨迹数据中的轨迹点不仅与上文轨迹有关系，还与下文轨迹有关系。如果只用上文轨迹进行学习，那么修复的轨迹点越多，误差越大。如果增加对下文轨迹信息的学习，两边同时修复缺失轨迹，将有效减少误差，保证轨迹修复结果的可靠性和准确性。然而，BP神经网络是一种单向学习的网络，想要实现上下文轨迹的双向学习，需要改进其网络结构。因此，本文基于BP神经网络设计了双向预测模型Bi-BPNNs，其结构如图1所示。输入层除了包含缺失轨迹的上文的特征向量，还增加了下文的特征向量，按时间顺序翻转之后再传输给网络的隐含层，在输出层的时候跟上文预测的正向轨迹结合，最终输出完整的轨迹修复结果。

2 模型构建与参数设置

2.1 模型输入

从采集的船舶AIS数据选取时间、经度、纬度、航向、航速为船舶轨迹特征向量，作为模型的输入变量。输入变量除了包含缺失轨迹的上文信息，即前一时间段的轨迹，还包括后一时间段的下文轨迹。因为船舶轨迹特征向量是有序的时间序列，所以下文的轨迹信息在输入隐含层之前还需要进行翻转，以便网络学习到下一时间段中有更多的轨迹特征，从而提高缺失部分轨迹的预测精度。

2.2 模型参数

轨迹修复模型的重要参数：1)时间步长过短会影响整体的学习效果，太长则泛化能力不好；2)隐含层神经元数目对网络的性能影响较大，也决定了网络的复杂度，是网络模型重要的参数；3)训练函数可通过调整权值和阈值来减小整体误差的算法；4)传递函数是网络的重要组成部分，而且必须是连续可微的。这些参数将通过实际轨迹数据的训练和测试实验进行选择和优化。

2.3 模型评估

通过训练值、预测值、真实值的RMSE (root mean square error,均方根误差)和MAE(mean absolute error,平均绝对误差)对构建的双向修复模型的轨迹修复结果进行评估和优化。同时，为验证构建模型的性能，还将其与常见的插值方法[11]和基础的BP网络[12]进行对比，并通过计算RMSE和MAE进行对比分析，计算方法:

3 实验及结果

本实验使用的船舶轨迹数据来源于航行在长江干线的一艘散货船，航行轨迹是长江干线江苏航段浏海沙水道，区域范围为31°55′53″N，120°29′49″E至32°8′38″N，120°46′1″E，航行时间为2018年10月13日。原始的采样数据包含日期、时间、船舶呼号、航速、航向、经度、纬度，部分数据如表1所示。

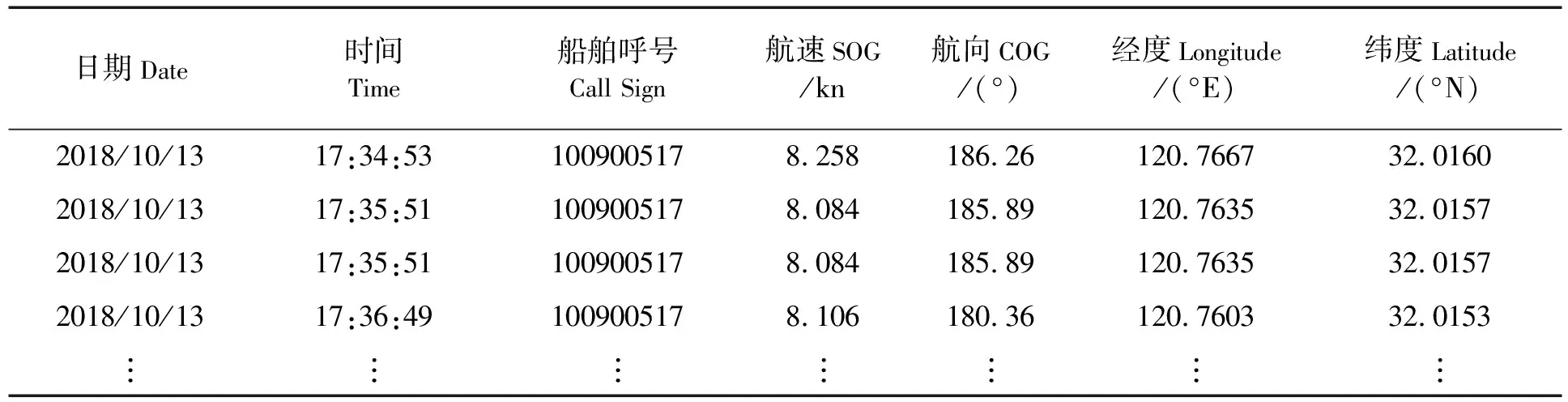
表1 部分原始采样数据

3.1 轨迹预处理

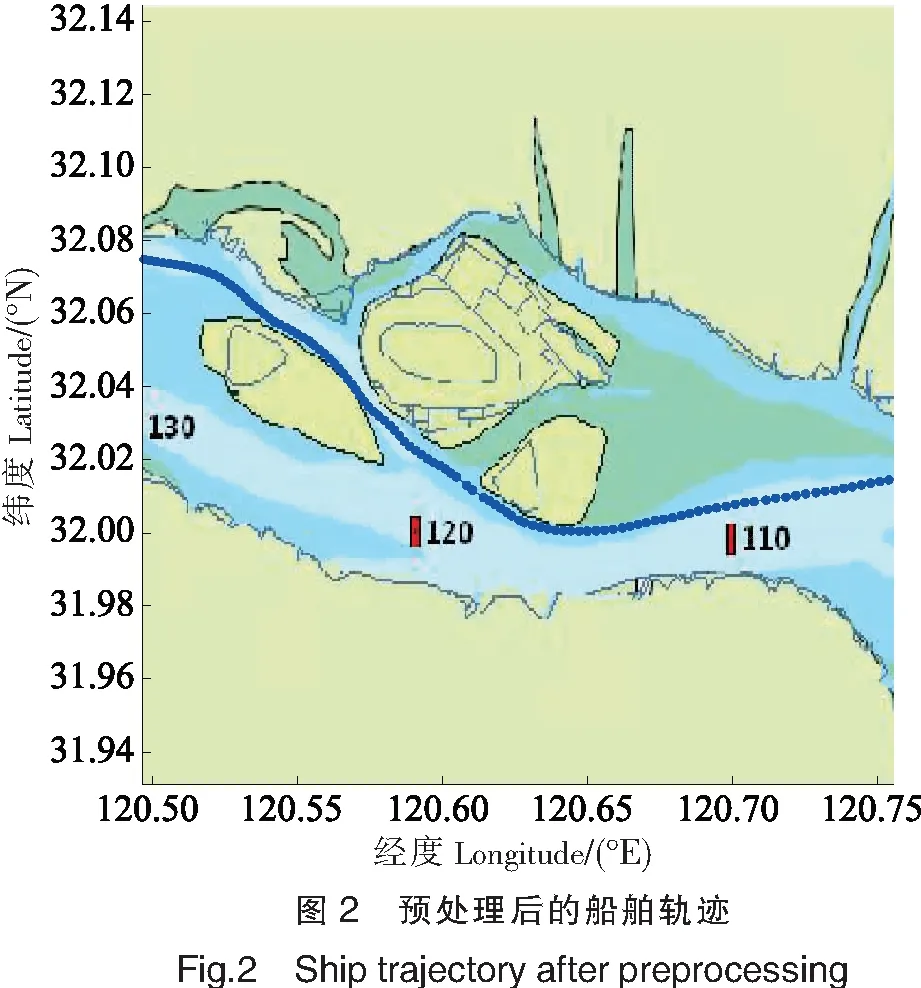
除了设备误差和网络传输造成的轨迹数据缺失外，采集到的原始数据还存在一些异常和噪声。例如，船舶的经度或纬度数据范围不在采样的航行区域范围，部分航速明显偏小或偏大。为此，设计了轨迹数据预处理方法：先将收集的原始数据按采样时间进行排序，删除重复的数据；接着对排完序的数据进行航段划分，以便在更小的范围内进行判断，避免下一步错误处理或清洗过度；然后在航段内进行遍历，分别判断经度、纬度、航速是否在正常范围之内，如果超出范围就被认为是异常数据被清洗掉，最终得到干净的轨迹数据集，预处理之后得到的船舶轨迹如图2所示。

3.2 船舶轨迹修复

为验证所构建的Bi-BNNs轨迹预测模型的性能，选取修复难度大的弯曲段轨迹进行实验，设置{航速,航向,经度,纬度}为修复模型的输入特征向量，并随机选取样本数据的80%作为训练集，剩下的20%为测试集。实验开始，将模型的参数神经元数量、时间步长、训练函数、传递函数分成4组进行测试，通过计算，比较模型的训练误差和测试误差，对各参数进行逐步优化，如表2所示。

从表2中的第1组和第2组实验中可以看到，当训练函数为“trainlm”、传递函数为“purelin”时，经度和纬度的训练误差最小；在第3组实验中，时间步长为4的误差比时间步长为2和5时的要小；同理，在第4组试验中，神经元数量为12时，模型的预测效果最佳。因此，最终设定轨迹修复模型的参数如下：神经元数量为12；时间步长为4；训练函数为“trainlm”；传递函数为“purelin”。这里，模型参数时间步长设置为4，也就说用4个历史轨迹数据点预测未来一个轨迹数据点，然后依次循环直至得到完整的轨迹预测。

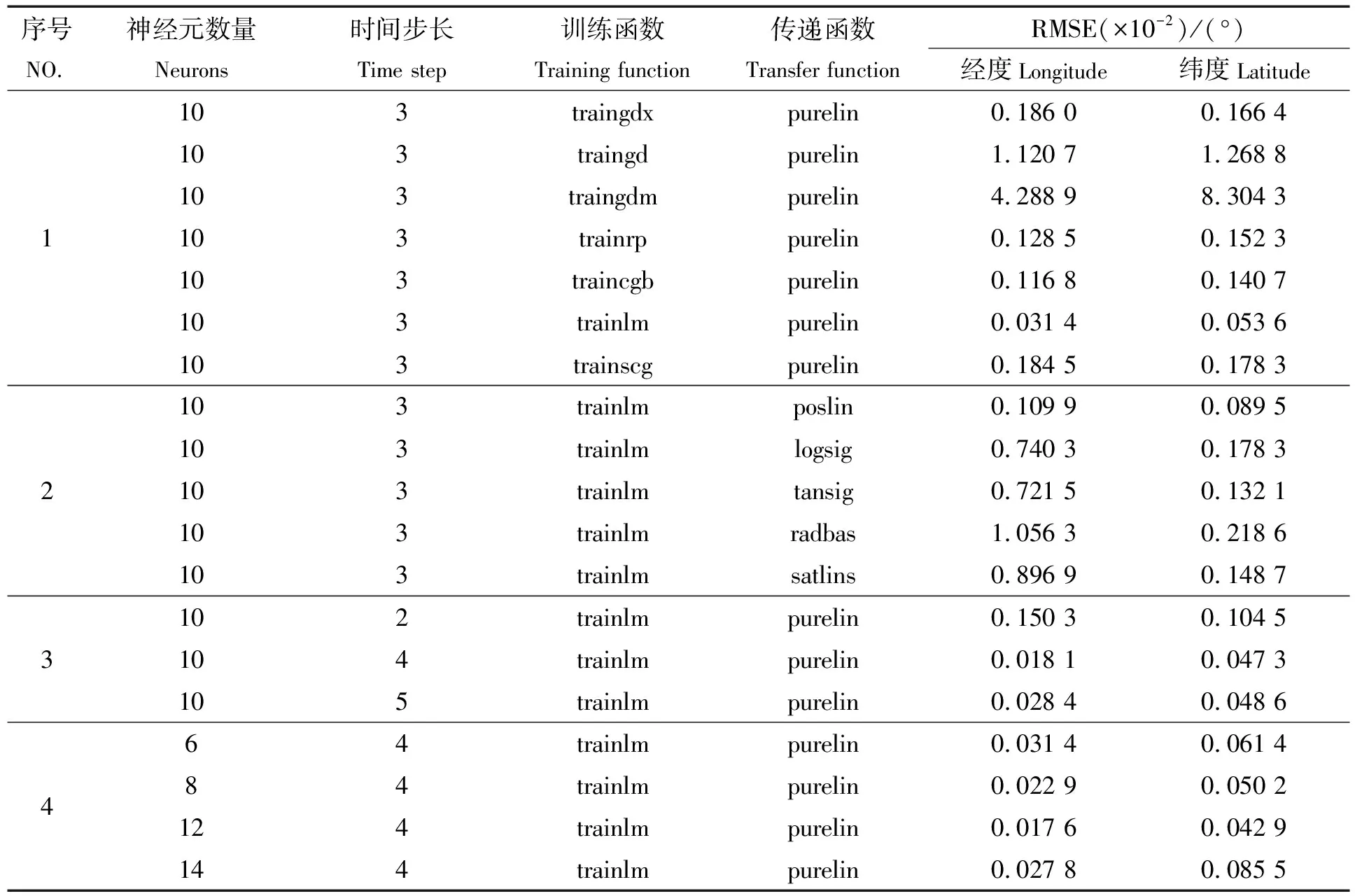
表2 Bi-BPNNs模型的不同参数设置实验

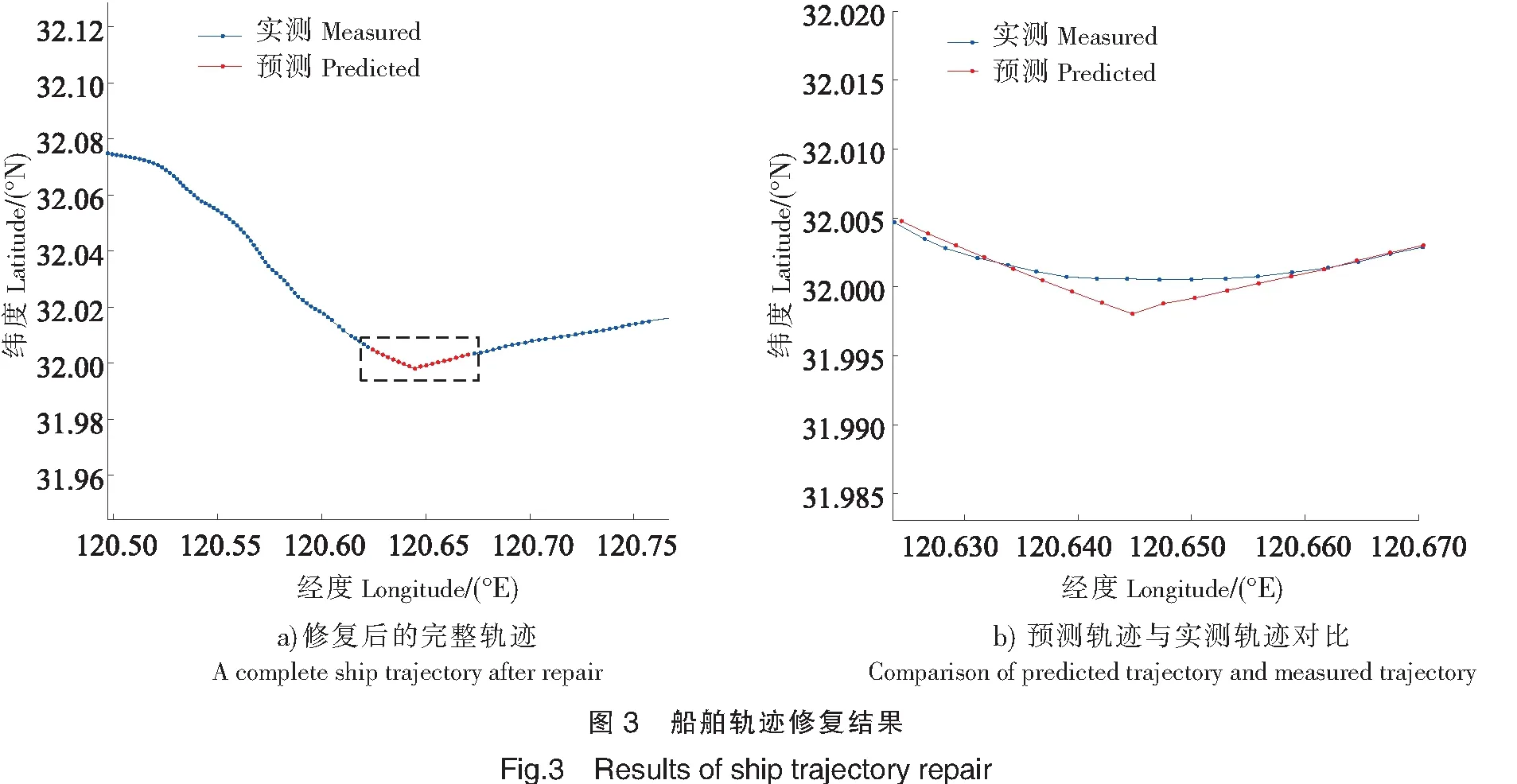
根据确定的双向预测模型，分别利用上下文的船舶轨迹点双向循环预测9个轨迹点，得到共含有18个预测轨迹点的轨迹,如图3所示。图3中，蓝色点表示真实测得的轨迹，红色点表示预测的轨迹，其中图3a)是包含预测信息的轨迹，图3b)是弯曲航段真实轨迹与预测轨迹的对比。图4展示了Bi-BNNs模型的船舶轨迹修复性能。

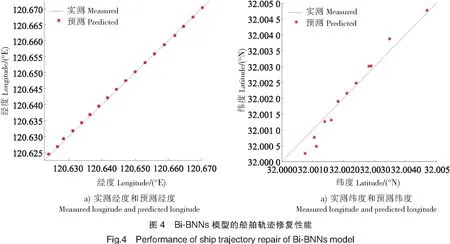
此外，为了进一步验证Bi-BPNNs模型的轨迹修复优越性，基于相同的实验数据，将其分别与常见的线性插值(linear interpolation,LI)[13]、逐段三次样条插值(spline interpolation,SI)[14]、立方插值(pchip interpolation,PI)[15]、和基础BP神经网络(BPNNs)模型进行对比，并计算各方法修复轨迹数据的RMSE和MAE，得到10次实验结果的平均值和标准差，如表3 所示。从表3中可以看出Bi-BPNNs优于其他的方法和模型。

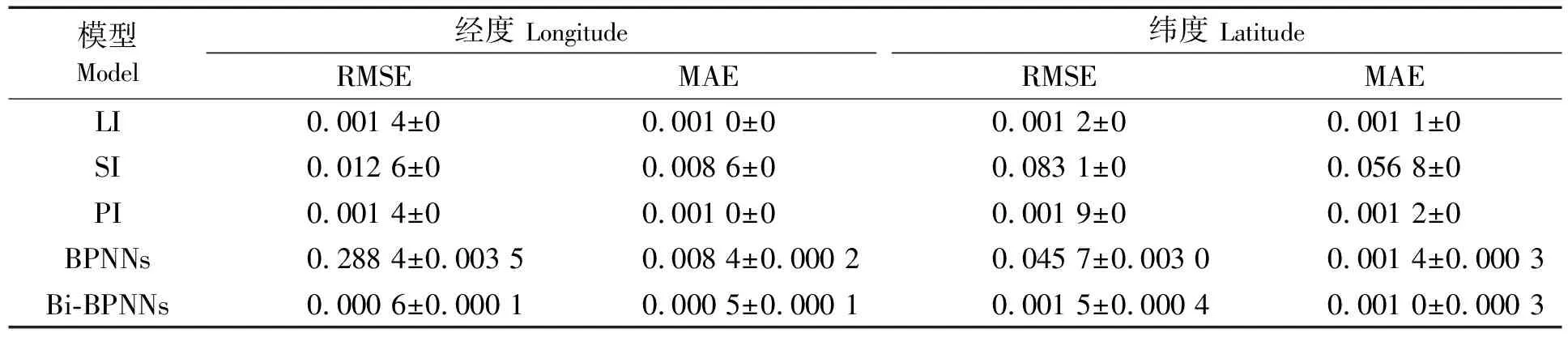
表3 不同模型的船舶轨迹修复模型性能

4 结论

本文针对船舶轨迹数据的缺失和异常问题，提出了Bi-BPNNs模型，利用对上下文的历史轨迹信息特征的学习，实现对缺失轨迹的双向循环预测，从而提升轨迹修复的精度和效率。弯曲航段的实例验证结果表明：经度修复的误差RMSE和MAE分别只有0.000 6和0.000 5；纬度修复的误差RMSE和MAE分别只有0.001 5和0.001 0。与其他多种插值方法和基础BP神经网络相比，本文提出的Bi-BPNNs在船舶轨迹修复上具有明显的性能优势。