集装箱用夹芯板抗爆性能仿真研究

2021-12-03陶思昊王文欣戚春保秦铭澳

兵器装备工程学报 2021年11期

陶思昊，王涛，王文欣，戚春保，秦铭澳

(1.火箭军工程大学核工程学院，西安 710025； 2.四川红华实业有限公司，四川乐山 614000)

1 引言

集装箱作为一种具有足够强度并能反复使用的大型装货容器，具有便于机械搬运、装卸便捷、保护货物等优点。随着军事装备的发展和军事局势的变化，集装箱除了用作货物周转箱之外，还可作为专用设备的方舱或者野战营房等，这些用途对集装箱的抗爆能力提出了更高要求。普通的集装箱普遍使用轻质钢结构和轻薄钢材料，只能抵挡一般外力，不具有防护冲击波的能力。因此设计出能够防爆炸冲击波的集装箱具有广泛的应用范围。

目前国内使用的抗爆结构主要是双层增强抗爆结构和三层夹芯抗爆结构。双层增强抗爆结构外层为表面镀锌的钢板，内层为增强纤维型硅酸钙材料，二者通过机械冲压贴附在一起，工艺较简单、成本较低，适合于对防爆性能要求不高的墙体结构[1]。三层夹芯抗爆结构选用高强度钢作为面板，内层用合成材料进行填充；另一种使用混凝土板作为面板，内层使用钢筋、水泥和填砂填充，被称为“复合抗爆墙”，有较好的抗爆效果，但整体质量较大，只适合作为固定的防爆结构[2]。顾太平等[3]利用泡沫铝具有较高且长的屈服平台和冲击吸能大的特性，设计船体泡沫铝冲击吸能器；田斌等[4]通过阐释冲击波在不同波阻抗材料中的传播原理，得出钢板-泡沫铝复合结构的缓冲吸能效果优于单层钢板；张培文等[5]通过改变表面钢板及泡沫铝芯层厚度，分析了夹芯板在爆炸载荷作用下的吸能规律；Zhu等[6]探究了夹芯结构在爆炸载荷下的变形模式；Radford等[7]探究了泡沫金属芯夹芯板对模拟爆炸荷载的响应过程。以上研究大多针对多层材料的叠加排布，很少对内部材料排布形状进行设计。

本文针对泡沫铝具有较好的能量吸收能力和高比刚度等性能[8]，提出一种钢板-泡沫铝组成夹芯结构作为集装箱的板材，在保持集装箱外形结构不变的情况下，通过在内侧增加抗爆层组成新的集装箱板，来提升其抗爆性能。运用数值仿真的手段，开展钢板、泡沫铝组成的不同夹芯结构在爆炸冲击波作用下的抗爆性能测试，对内部结构进行优化设计，得出抗爆性能最佳的钢板-泡沫铝夹芯结构。

2 仿真模型的建立

2.1 几何模型的建立

设计建立3种钢板-填充泡沫铝波纹夹芯结构[9]，截面尺寸如图1所示，单位为cm。集装箱板是由最外层的集装箱瓦楞面板和内层的“三明治”夹芯结构组成方板，其中芯层的等边三角形波纹结构的底角有30°、45°和60°等3种。集装箱瓦楞面板、夹芯结构中的波纹结构选用钢板，填充的三棱柱泡沫铝的截面三角形底角与钢板相配合，分别为30°、45°和60°。

图1 钢板-泡沫铝夹芯结构截面示意图

集装箱瓦楞面板、夹芯结构面板、波纹钢板部分厚度为毫米级，相比于整体尺寸而言厚度较小，故采用壳单元—SHELL163单元[10]，通过关键字定义其厚度，使用面网格划分技术进行网格划分，保证面网格为高质量四边形；波纹结构中填充的三棱柱泡沫铝采用结构实体单元—SOLID164单元[10]，使用扫掠网格划分技术进行体网格的划分，保证体网格为高质量六面体，结果如图2所示。集装箱瓦楞面板与夹心结构面板、夹心结构与泡沫铝，通过共节点的方式模拟焊接关系。

图2 底角30°的钢板-泡沫铝夹芯结构网格模型示意图

本文中面板采用四边固支约束，选定各边界5 cm区域的节点，通过关键字*BOUNDARY_SPC_SET定义四边固定。同时为模拟无限域，板的边界设定为非反射边界，用来阻断应力波在模型边界处的反射现象。在集装箱瓦楞面板与夹芯结构钢板、夹芯结构钢板与泡沫铝之间，通过关键字*CONTACT_AUTOMATIC_SURFACE_TO SURFACE施加双向的面面接触，使用关键字*CONTACT AUTOMATIC_SINGLE_SURFACE为夹芯结构创建单面自接触。

TNT炸药从面板中心正上方100 cm处爆炸，使用关键字*LOAD_BLAST_ENHANCED定义炸药爆轰压力荷载的空间位置、TNT炸药质量及起爆时间[11]。

2.2 材料模型的建立

泡沫铝采用*MAT_CRUSHABLE_FOAM模拟缓冲材料模型，夹芯结构表面钢板和内部波纹形钢板采用*MAT_PLASTIC_KINEMATIC弹塑性材料模型[12]。2种材料的主要材料参数见表1，泡沫铝使用达到密实应变时对应的应力。参照前期实验测得的泡沫铝应力-应变数据[13]，如图3所示，并在计算文件中加载。

表1 泡沫铝与钢的主要参数

图3 泡沫铝的应力-应变曲线

3 集装箱板抗爆性能仿真计算

3.1 仿真模型有效性验证

为消除网格大小的不合理对数值模拟结果产生的影响，对计算模型的收敛性进行检验，选取5 cm、3 cm、2 cm、1 cm、0.8 cm和0.5 cm等6种网格大小，使用Hypermesh划分网格并进行单元质量和连续性检验，网格模型结果如图4所示。

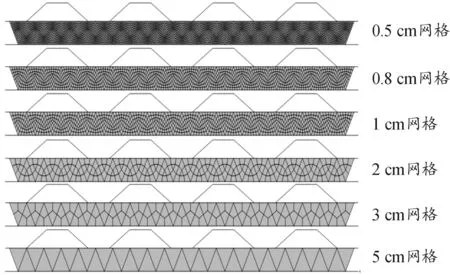
图4 不同尺寸的网格模型示意图

函数*LOAD_BLAST_ENHANCED产生的冲击波能量将转化为靶板的动能和内能，图5为5 kg TNT炸药爆炸时，不同网格大小的60°底角夹芯结构仿真模型的内能吸收值曲线。由图5可以看出，网格较粗糙时(大小为5 cm、3 cm和2 cm时)，能量吸收值的结算结果分散性较大，随着网格尺寸的减小，靶板的能量吸收值逐渐趋于稳定，当网格尺寸为 1 cm、0.8 cm和0.5 cm时，靶板能量吸收值达到最大，并基本保持在一个相对稳定的小区域内波动，再减小网格尺寸不会较大程度地提高计算精度，但会使计算量增大，计算时间大幅度增加，导致计算效率降低。综合考虑计算精度和计算效率，故采用1 cm大小的网格划分方式建立模型并进行数值模拟。

图5 不同尺寸网格模型的内能吸收值曲线

3.2 爆炸载荷作用下集装箱板的动态响应

本文研究炸药质量为1 kg、2 kg、3 kg、4 kg和5 kg等5种爆炸载荷，在爆炸比高为100 cm不变的情况下，波纹夹芯板角度分别为30°、45°和60°等3种结构的抗爆性能。

计算结果显示，在不同爆炸载荷下，3种靶板具有不同程度但相似的变形模式。3 kg TNT炸药爆炸作为一个较为中间的情况，可以反映靶板平均的变形状态。图6为3 kg TNT在钢板-泡沫铝夹芯结构正上方100 cm处起爆时，底角为30°的钢板-泡沫铝夹芯结构的动态响应过程。

图6(a)～图6(e)分别为选取钢板-泡沫铝夹芯结构在爆炸作用下t=0、0.5 ms、1 ms、1.5 ms、2 ms时垂直于板方向(Y方向)的位移云图。0 ms时炸药开始起爆，0～1 ms时，钢板-泡沫铝夹芯结构的变形主要是集装箱瓦楞钢板的变形，其被压紧至夹芯结构钢板表面；0.5 ms时夹芯结构开始发生变形，夹芯结构的表面钢板被压凹，夹芯结构中的波纹钢板与夹芯结构的上下面板接触处附近开始产生局部塑性弯曲变形，填充泡沫铝发生塑性变形，开始吸能，0.5 ms到2 ms这段时间是夹芯结构的吸能过程；2 ms时夹芯结构中心点位移达到最大值2 cm，夹芯结构内部波纹钢板发生塑性变形，泡沫铝发生胞壁断裂的致密变形[14]。

图6 底角30°的钢板-泡沫铝夹芯结构的动态响应过程的位移云图

3.3 不同钢板-泡沫铝夹芯结构的能量吸收

选取整个防爆结构，提取数据得到3种靶板在5种TNT质量下的能量吸收，如表2所示，绘制其能量吸收与炸药质量的关系曲线，如图7所示。

表2 5种爆炸载荷下3种夹角结构的能量吸收值

图7 5种爆炸载荷下3种夹角结构能量吸收曲线

分析计算数据可得，在相同TNT质量下，三角形底角为30°的钢板-泡沫铝夹芯结构的能量吸收值最大，底角为45°时次之，底角为60°时能量吸收值最小，3种靶板的能量吸收值随TNT炸药质量的增加而增长，呈线性关系[15]。而当炸药质量较小，即较弱的爆炸载荷作用下，3种结构的能量吸收差别不大，主要是结构的吸能能力没有得到充分发挥。

3.4 爆炸中心点对应的靶板后表面的挠度

挠度是板材或构件垂直于中心面的位移量，夹芯结构的抗冲击性能通常以后面板中心点的最终挠度作为评价指标[10]。从结果文件中提取爆炸中心点对应的靶板后表面的最大线性位移，即挠度。图8为5 kg TNT质量下3种夹角结构的中心点挠度-时间变化历程曲线。

图8 5 kg TNT质量下3种夹芯结构中心点挠度历程曲线

分析不同TNT质量下的靶板中心点位移曲线趋势和特点，可以得出：随着TNT质量的增加，3种结构达到最大形变的时间逐步后移，三角形底角为60°的钢板-泡沫铝夹芯结构最早达到最大形变，底角为30°的钢板-泡沫铝夹芯结构达到最大形变需要时间最长。提取5种工况下靶板后表面最大挠度，如表3所示。在不同TNT质量、距离100 cm处爆炸时，三角形底角为60°度的钢板-泡沫铝夹芯结构的挠度均最小，其平均挠度为30°夹芯结构的59.5%，为45°夹芯结构的88.4%。底角为30°的钢板-泡沫铝夹芯结构变形最大，说明在相同爆炸载荷作用下，3种底角的钢板-泡沫铝夹芯结构中三角形底角为60°度的钢板-泡沫铝夹芯结构的刚度较大。

表3 爆炸后3种结构的中心点挠度

4 平均冲量与中心点挠度的无量纲处理

对某设备转运集装箱的要求是在受到爆炸载荷作用时，箱体的变形量不至于对内部设备造成损坏。集装箱箱体的大变形会影响内部产品的安全，所以钢板-泡沫铝夹芯结构在爆炸载荷作用下变形越小，其抗爆性能越好。但为便于部署与运输，也要尽量减少钢板-泡沫铝结构的重量。

4.1 平均冲量的无量纲处理

考虑到由于波纹板的角度不同，单位距离内钢材料的占比不同，这将影响到靶板的变形。为去除波纹板不同角度时材料占比对冲量的影响，应对冲量进行无量纲处理。图9为钢板-泡沫铝夹芯结构尺寸示意图，钢板密度为ρs，屈服强度为σr，泡沫铝密度为ρc。直线区域表示厚度为hf的钢板，三角形区域表示填充泡沫铝。设钢板-泡沫铝夹芯结构总厚度为H，长度为L，三角形高度为hc，相等的两边长度为lc，底边长为l，底角夹角为θ。则平均冲量I的无量纲处理公式推导过程为：

三角形底边长为：

l=2hccotθ

(1)

图9 钢板-泡沫铝夹芯结构尺寸示意图

板材具有的波纹三角形数目为：

(2)

则波纹形钢板总面积为：

(3)

三角形总面积为：

(4)

上下两侧面板总面积为：

SL=2hfL

(5)

则单位面积的无量纲平均冲量为：

(6)

表4 不同质量TNT炸药在100 cm的平均冲量

表5 不同爆炸载荷作用到3种夹芯结构的无量纲冲量

4.2 板材中心点挠度的无量纲处理

(7)

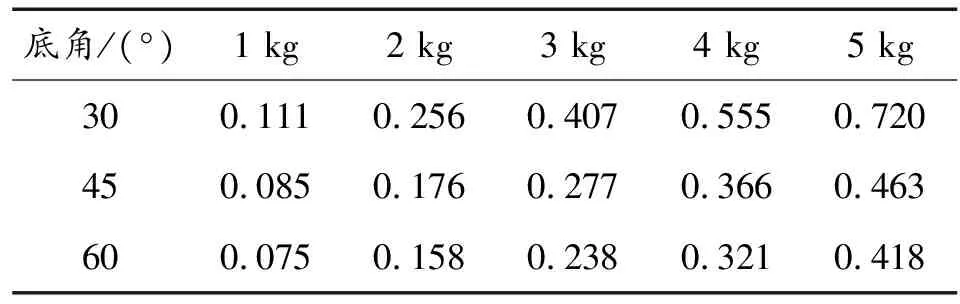
表6 板材中心点无量纲挠度

4.3 无量纲挠度和无量纲冲量的关系曲线分析

将表5中的无量纲冲量数据作为x轴，表6中的无量纲挠度数据作为y轴，绘制无量纲挠度和无量纲冲量的关系曲线，如图10所示。

通过无量纲挠度和无量纲冲量的曲线趋势与位置关系可得出：在同一无量纲冲量作用时，三角形底角为45°和60°的钢板-泡沫铝夹芯结构挠度明显小于三角形底角为30°的钢板-泡沫铝夹芯结构，说明夹芯结构选用这2种底角时抗爆性能较好。但底角为45°时夹芯结构内部瓦楞形钢板总长度小于底角为60°的，所以在抗爆性能接近的情况下，底角为45°的夹芯结构重量小于底角为60°的夹芯结构。在相同距离、相同爆炸载荷作用下，可以认为三角形底角为45°度的钢板-泡沫铝夹芯结构的抗爆性能最好。