钢管混凝土箱形叠合墩振动台试验研究

袁辉辉，佘智敏，吴庆雄,3，黄育凡，陈康明

(1.福州大学土木工程学院，福建，福州 350116；2.福建省土木工程多灾害防治重点实验室，福建，福州 350116；3.工程结构福建省高校重点实验室，福建，福州 350116)

钢管混凝土(CFST,concrete-filled steel tube)箱形叠合墩是以钢管混凝土为核芯，外包一层厚度较薄的普通钢筋混凝土，并通过钢筋混凝土腹板将各柱肢连接形成具有箱形截面的结构。近年来已开展的CFST箱形叠合墩在轴压[1−3]、偏压[4 −5]、轴拉[6]、弯曲[7−8]和承载能力极限状态[9 −10]作用下的受力性能研究表明：由于内部钢管混凝土部件和外包钢筋混凝土部件之间的相互作用，CFST箱形叠合墩比钢管混凝土格构墩和钢筋混凝土薄壁墩具有更高的承载力和稳定性。同时，Wang等[11]、Ma等[12]采用低周往复荷载试验和有限元分析方法，进行了CFST箱形叠合柱和钢筋混凝土空心柱的滞回性能研究，发现与钢筋混凝土空心柱相比，CFST箱形叠合柱的承载力、延性、耗能能力均有显著的提高。吴庆雄等[13]以柱肢间距和轴压比为参数开展了CFST箱形叠合墩缩尺模型的拟静力试验研究，提出了有较高精度的水平承载力计算方法。

由上述研究可知，CFST箱形叠合墩综合了钢管混凝土叠合柱承载力高、耐久性好、延性好[14−15]和钢筋混凝土空心墩抗弯刚度大、自重轻[16]等优点，具有优越的抗震性能。因此，此类桥墩逐渐在我国西部地震多发区高墩桥梁中得到应用，如雅泸高速公路上的腊八斤特大桥和黑石沟特大桥，以及国道356线上的金阳河特大桥。然而，目前新建和在建的CFST叠合空心墩桥梁大都没有经历过强震的考验，震害资料缺乏，相关结构地震响应研究仍局限在有限元模拟分析上，其抗震设计理论和方法研究仍存在不足，影响了此类新型组合结构在高烈度地区桥梁工程中的推广应用。

因此，为充分了解强震作用下CFST箱形叠合高墩的非线性地震响应特性，本文以腊八斤特大桥11号墩为原型，设计并制作了几何相似比为1∶9.43的缩尺模型，开展CFST箱形叠合墩的振动台试验研究，并结合空间杆系非线性有限元分析，进一步研究此类桥墩的非线性地震响应和破坏机理。相关研究成果可为CFST箱形叠合墩在高烈度地区的工程应用提供一定的理论支撑和指导。

1 CFST箱形叠合墩缩尺模型振动台试验设计

1.1 依托背景工程

如图1所示，腊八斤特大桥主桥为四跨变截面连续刚构桥，跨径布置为105 m+2×200 m+105 m。该桥桥墩采用分幅式CFST箱形叠合墩，9号～11号主墩墩高分别为141.64 m、182.64 m和87.76 m。9号墩和10号墩墩顶纵桥向宽10 m，11号墩顶宽9 m，均按70∶1的比例向下变宽；主墩横桥向等宽为6.8 m。

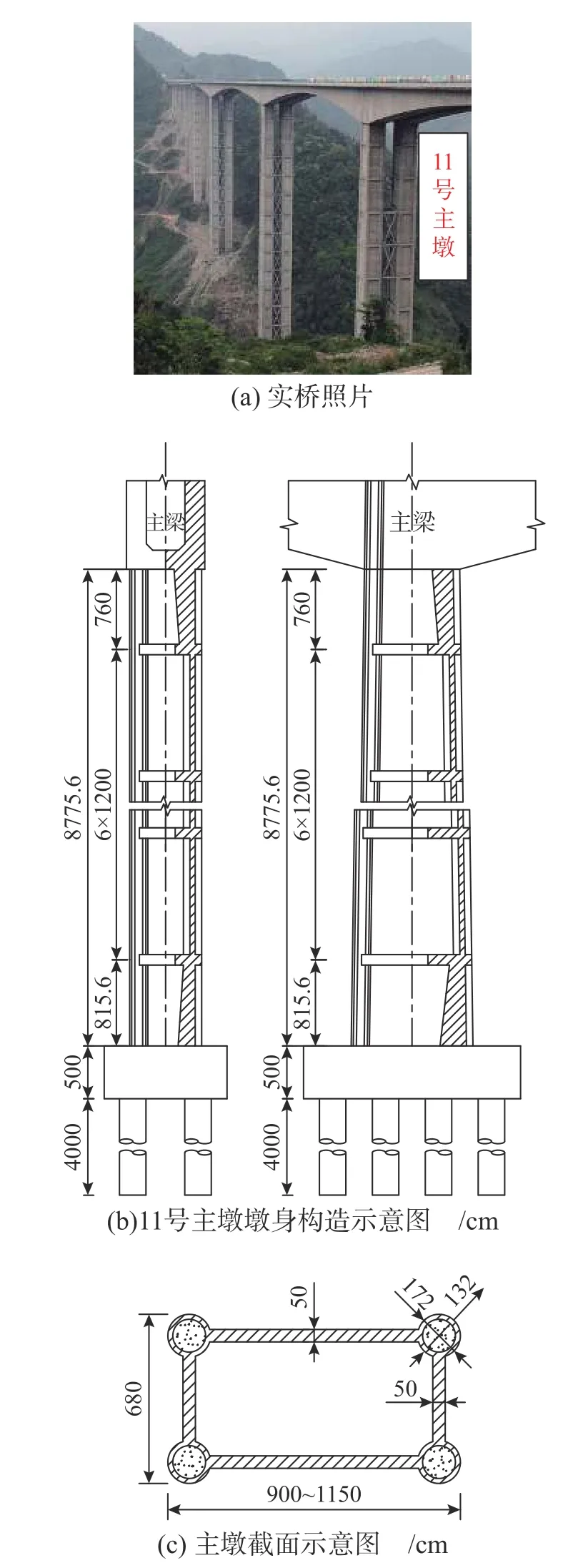
图1 依托背景工程——腊八斤特大桥Fig.1 Engineering background -Labajin Bridge

外包层钢筋混凝土厚度为20 cm，腹板厚为50 cm，沿墩高每隔12 m设置一道100 cm厚水平加劲预应力钢筋混凝土隔板。9号、10号和11号墩的CFST格构柱骨架均由4根管径为1320 mm的钢管混凝土组成，钢管壁厚由墩顶的14 mm变化为墩底的18 mm。9号和10号墩钢管内灌注C80混凝土，11号墩钢管内为C60混凝土，外包混凝土强度均为C30，钢管采用Q345钢材，钢管混凝土柱间用型钢连接。本次振动台试验研究以腊八斤特大桥11号主墩的单幅为原型，进行缩尺模型的设计和制作。

1.2 试验模型设计

本次试验在福州大学的地震模拟振动台[17]上进行，振动台台面尺寸为4 m×4 m，最大载重22 t，包含水平双向和水平内转动3个自由度。台面满载情况下最大加速度可达1.5 g，抗倾覆力矩为550 kN·m，台面有效行程为±250 mm，频率范围0.1 Hz～50 Hz。根据已开展的CFST叠合箱形墩的拟静力试验结果[13]，CFST格构柱是此类桥墩的主体受力骨架，钢筋混凝土腹板参与抗剪、提高桥墩抗推刚度，因此在进行本次试验缩尺模型的设计时，以柱肢钢管的截面尺寸为主要控制因素，并综合考虑振动台的规格尺寸和载重能力、模型制作难易等因素，确定试验模型采用的柱肢钢管直径为140 mm，与实桥采用的直径1320 mm钢管的几何缩尺比例为1∶9.43。

采用上述缩尺比例设计制作的模型如图2所示，模型总高10.81 m，墩身高9.31 m，墩顶柱肢中心纵桥向间距0.78 m、横桥向间距0.54 m，墩身纵桥向按70∶1比例放坡，横桥向等宽。为便于制作，对桥墩部分构造和尺寸参数进行适当的调整：若按照1∶9.43的比例进行缩尺，腹板厚度为53 mm，钢管外包混凝土厚度为21 mm，会导致混凝土浇筑困难、加工质量无法保证，故将外包混凝土厚度调整为50 mm，腹板厚度调整为70 mm；根据刚度等效原则，实桥中的横撑和斜撑分别简化为Ф48 mm×2.0 mm和Ф38 mm×1.5 mm的空钢管，腹板钢筋为HPB300Ф6钢筋，并取消横隔板和风撑构造。虽然上述简化措施会使试验模型相比理论缩尺模型的纵桥向刚度提高了约23%、横桥向刚度提高了约17%，但墩柱主体结构形式并未发生改变，并根据原型与模型的频率比压缩输入地震动的持时，以保证真实反映原型桥墩的地震响应特性。此外，由于缩尺模型高度超过10 m，为便于制作和安装，将缩尺模型由上至下依次划分为三个节段，各节段之间通过钢板焊接和螺栓连接的方式进行组装。

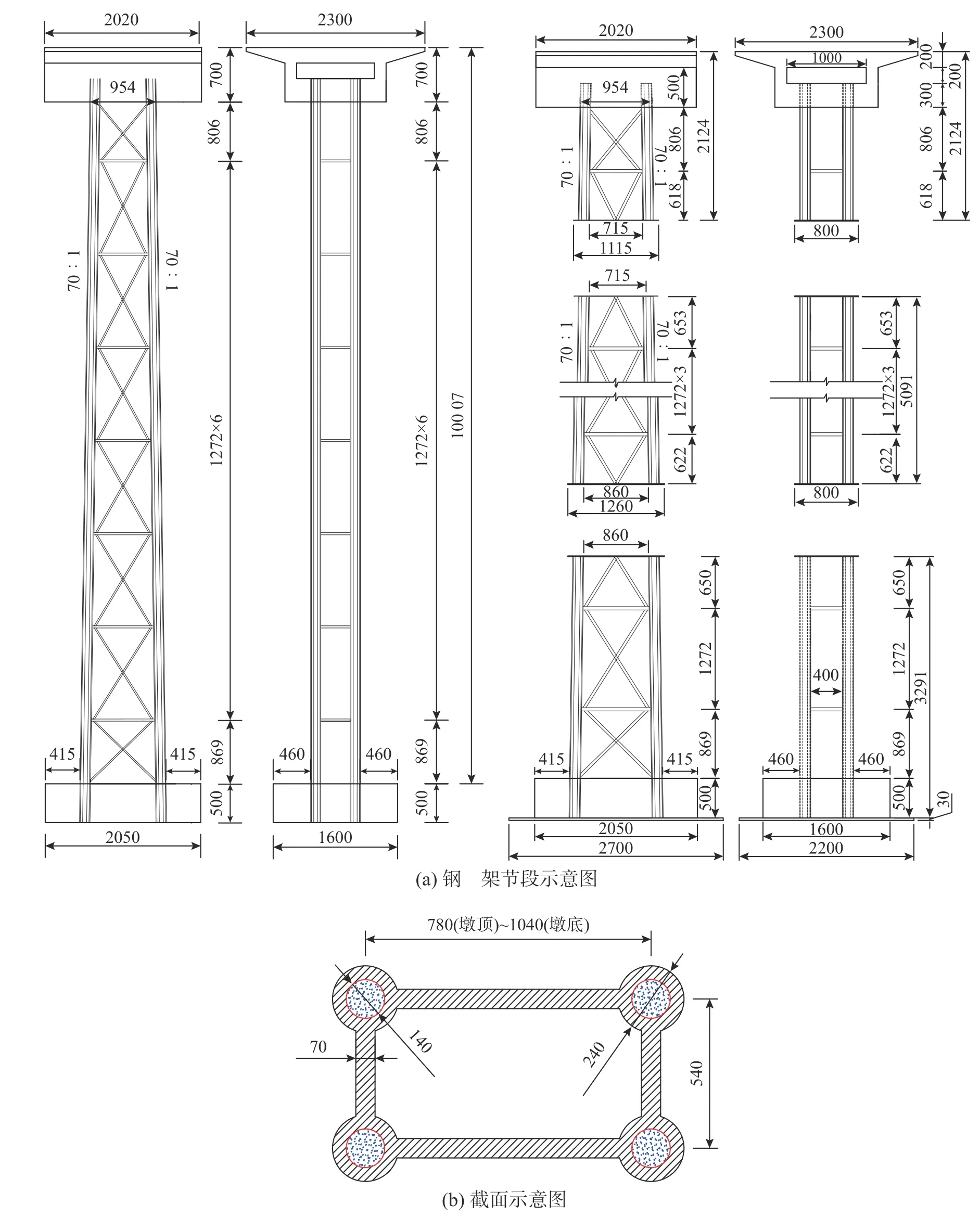
图2 振动台缩尺模型构造示意图 /mmFig.2 Structural schematic diagram of scaled model for shaking table test

表1为试验模型主要构造参数，表2为试验材料的性能指标。试验模型墩底设置的2.0 m×1.3 m×0.5 m承台内预留螺栓孔，通过螺栓将试验模型与振动台台面固结，如图3所示。试验模型重6.8 t，承台重量为3.4 t，由于振动台的承重能力为22 t，只能采用欠人工质量法进行配重，人工配重通过浇筑在墩顶的具有主梁形状的柱帽和锚固在柱帽上的工字钢来实现，可模拟墩梁固结的受力特性，人工配重质量为10.2 t。得到采用欠人工质量法配重的模型理论相似关系，见表3。

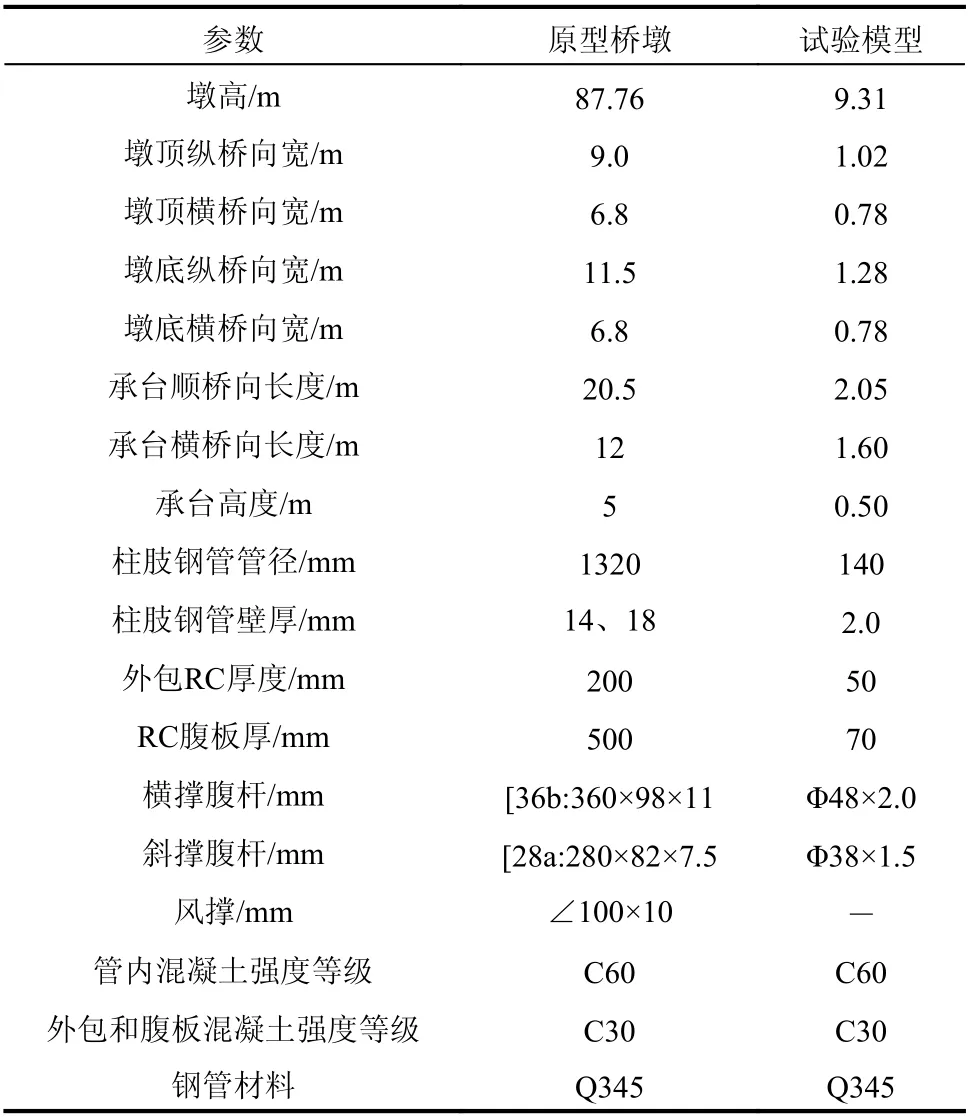
表1 试验模型参数Table1 Parameters of test specimen

表2 材料性能试验结果Table2 Results of material properties test

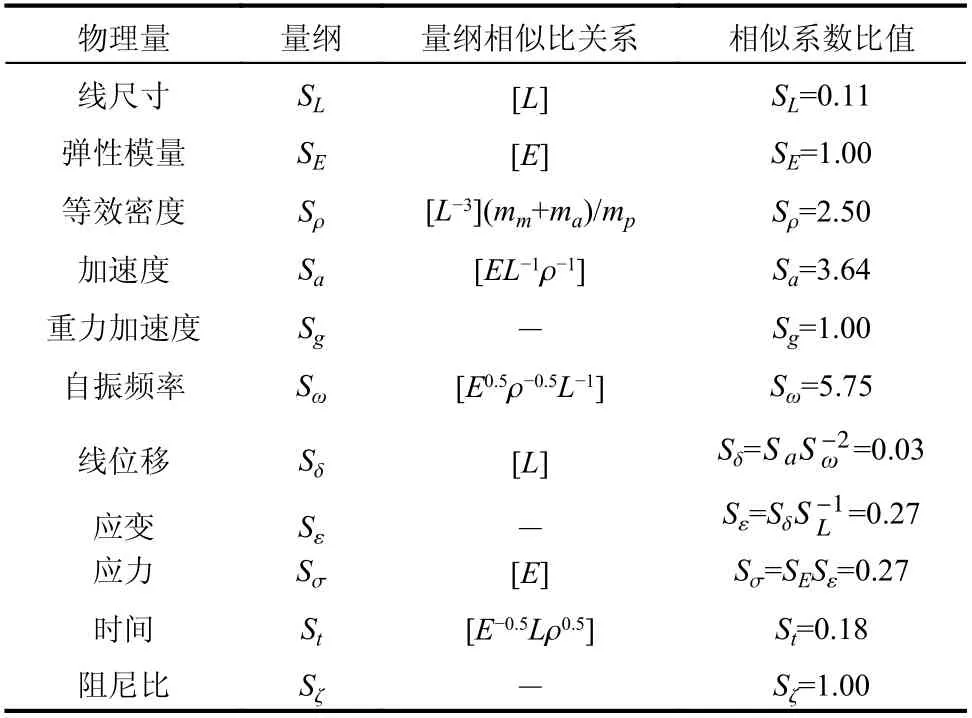
表3 模型理论相似系数Table3 Similarity coefficient of specimen

图3 振动台试验照片Fig.3 Photo of shaking table test

1.3 测点布置方案

振动台试验测试项目包含位移、加速度和应变，各类测点布置示意图如图4所示。

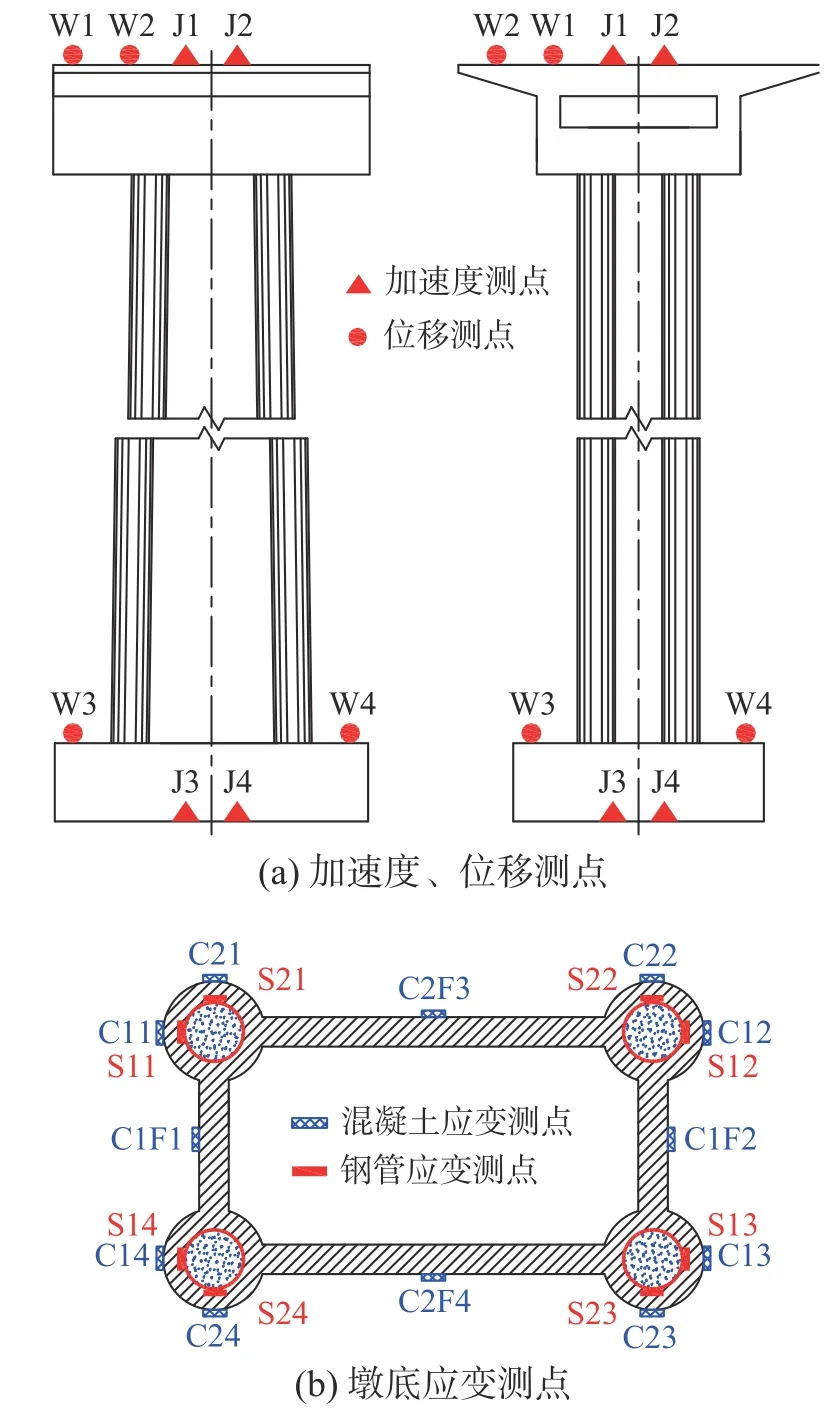
图4 测点布置示意图Fig.4 Layout of measuring points

墩顶处各布置2个加速度传感器和2个拉线式位移计，以测得墩顶纵桥向和横桥向的加速度和位移，墩顶加速度传感器编号分别为J1和J2，位移计编号分别为W1和W2；墩顶拉线式位移计的另一端固定在模型周围搭设的钢管脚手架上，为了验证台面输出的加速度与输入的加速度是否一致，在振动台台面布置纵桥向和横桥向的加速度传感器各1个，编号为J3和J4；为了测得墩顶相对台面的相对位移，在墩底处布置纵桥向和横桥向的拉线式位移计各1个，编号为W3和W4。应变测点布置在墩底截面，包含8个外包混凝土应变测点、4个腹板混凝土应变测点和8个钢管应变测点，共计20个应变测点。

1.4 试验工况设计

图5为本次振动台试验的输入地震动，表4列出了设计的加载工况。

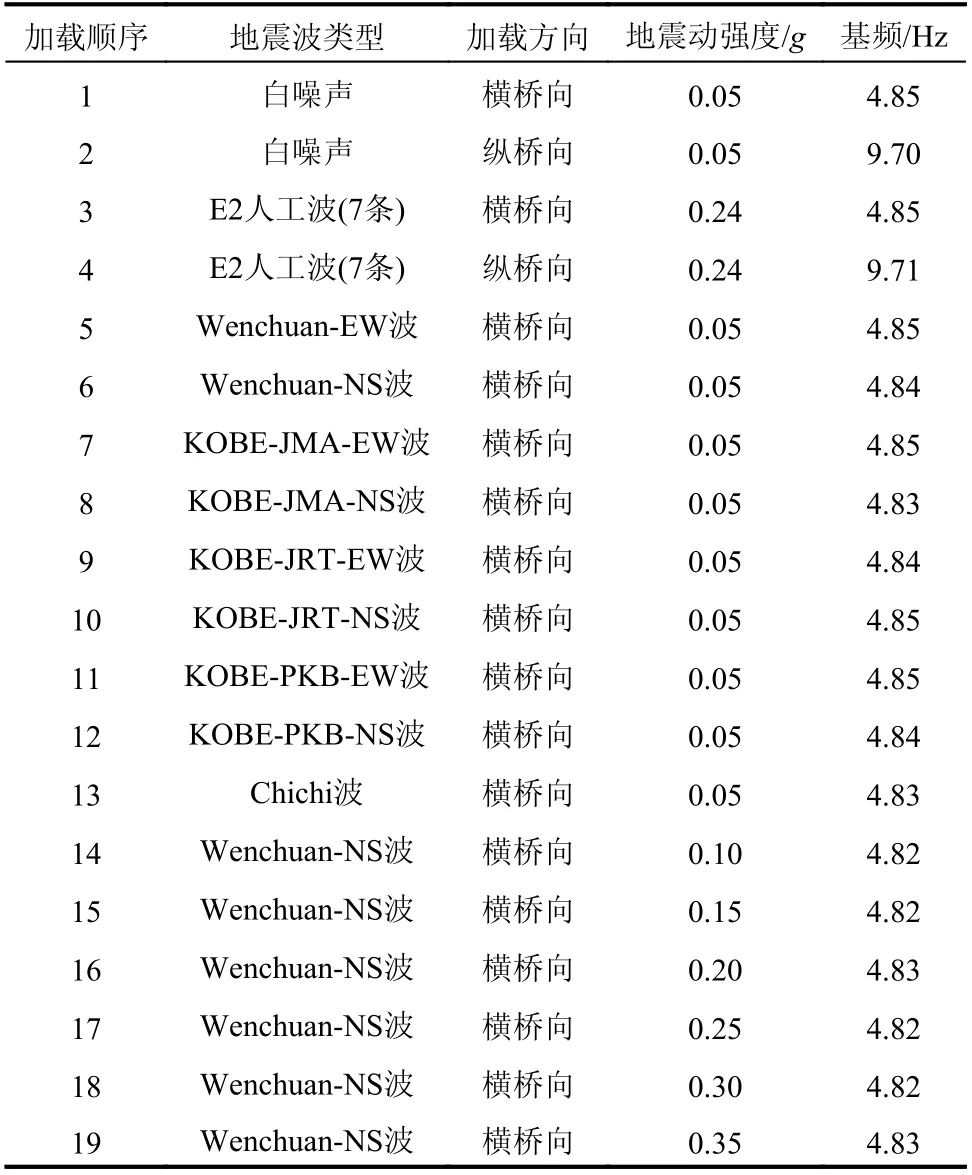
表4 试验加载工况列表Table4 List of test loading conditions

首先，进行CFST箱形叠合墩缩尺模型的基本动力特性试验，获取试验模型面外和面内一阶基频，并与原型桥墩的基频进行对比，确定输入地震波的时间压缩比例。同时在后续每次地震波工况加载前后都进行一次白噪声扫描，通过分析得到的缩尺模型基频来判断试验模型的刚度是否发生变化。

然后，分别在横桥向和纵桥向进行E2罕遇地震人工地震波的工况加载，验证CFST箱形叠合墩是否满足现行《公路桥梁抗震设计规范》[18]中规定的抗震设防目标要求，并确定地震波的最不利输入方向。根据设计资料，腊八斤特大桥抗震设防烈度为Ⅷ度，场地类型为Ⅱ类，特征周期Tg=0.45 s，抗震重要系数Ci=1.7，场地重要系数Cs=1.0，阻尼调整系数Cd=1.0，水平向设计基本地震动加速度峰值A=0.2 g。设计加速度反应谱如图5(a)所示，通过频响变换关系生成相应的7条E2地震加速度时程曲线，图5(b)为其中1条E2人工地震波，最大峰值加速度为PGA=0.24 g。

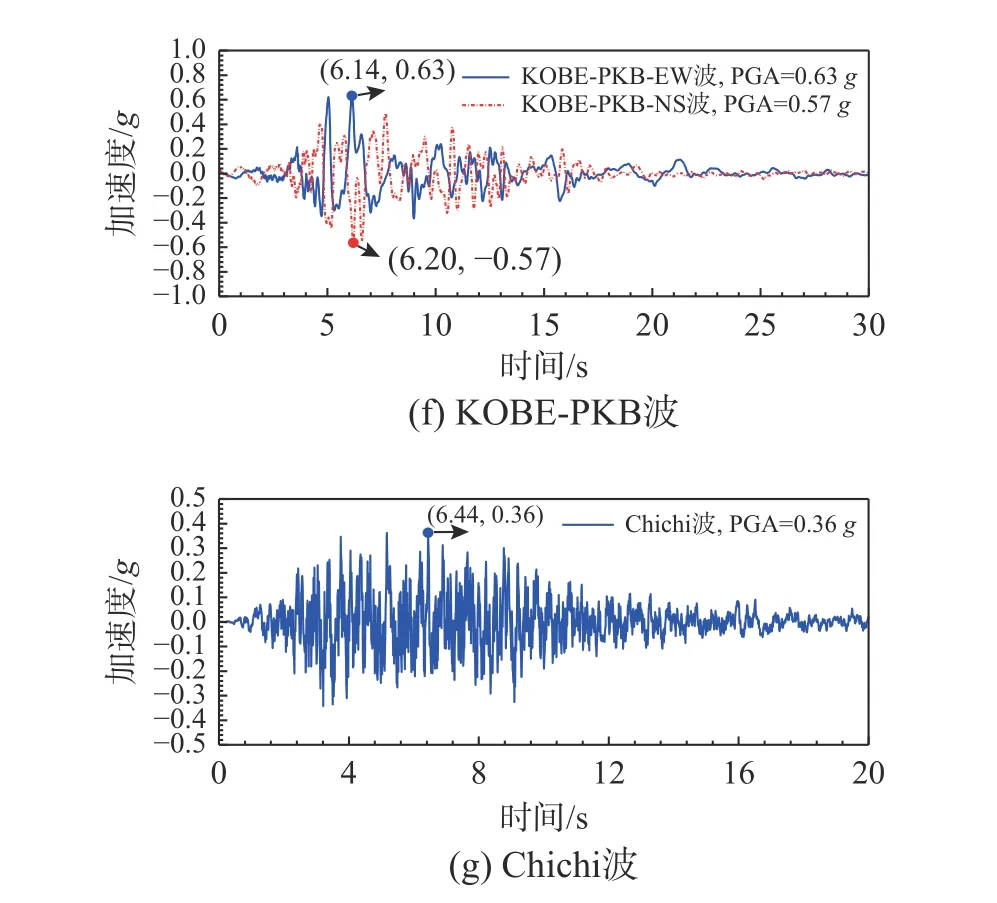
图5 地震动加速度时程曲线及反应谱Fig.5 Acceleration time history curve and response spectrum

E2人工地震波工况加载结束后，确定出地震波的最不利输入方向为横桥向。接着，选取如图5(c)～图5(g)所示的9条典型强震记录，均以地震动强度PGA=0.05 g沿横桥向输入，研究地震动特性对CFST箱形叠合墩地震响应的影响，为将来此类桥墩在不同场地条件下的推广应用提供一定的参考。

最后，根据典型强震工况的试验结果，选择地震响应最大的一条地震波(Wenchuan-NS波)，地震动强度按0.05 g的量级递增，直至倾覆力矩超过振动台的最大抗倾覆力矩，或结构破坏，无法继续承载，研究地震动强度对地震响应的影响。

2 基于纤维梁柱单元的有限元模型

2.1 单元网格划分

为了准确得到试验缩尺模型与实桥原型桥墩的频率相似比，本文建立实桥桥墩的有限元模型，并计算其固有模态，通过与试验模型的固有模态进行对比，从而确定输入地震波的时间压缩比例。

在既往经试验验证过的钢管混凝土结构[19]、钢管混凝土格构墩[20]、钢管混凝土混合墩[21]数值仿真模拟分析基础上，本文采用有限元软件OpenSees建立腊八斤特大桥11号主墩基于纤维梁柱单元的有限元模型，如图6所示，模型共184个节点和352个单元。图6(a)展示的桥墩墩底区域单元网格中，柱肢单元和混凝土腹板单元底部均固结。4根钢管混凝土叠合柱肢和4片腹板分别采用基于纤维梁柱单元模拟，每个单元设置5个积分点。其中，钢管混凝土叠合柱肢单元(图6(a)单元①)的钢管沿圆周方向30等分、沿径向2等分，管内混凝土沿圆周方向30等分、沿径向14等分，外包混凝土沿圆周方向30等分、沿径向8等分。需要说明的是，与已开展的拟静力试验[13]相同，本次振动台试验中钢管混凝土箱形叠合墩的柱肢钢管表面有焊接间断的竖向钢筋以加强钢管与外包混凝土的粘结性能，既往试验和本次试验均未发现外包混凝土与钢管出现剥离或错动现象，因此采用基于纤维梁柱单元模拟钢管混凝土叠合柱肢是可行的；腹板单元(图6(a)单元②)沿长度方向70等分、沿宽度方向7等分；钢管混凝土叠合柱肢单元和腹板单元之间通过弹性梁柱单元连成整体(图6(a)单元③)，并根据腹板厚度定义其截面特性。管内混凝土和钢管采用文献[22]建议的本构模型，如图6(b)和图6(c)所示。外包混凝土和腹板混凝土采用图6(d)所示Kent-Scott-Park本构[23]。

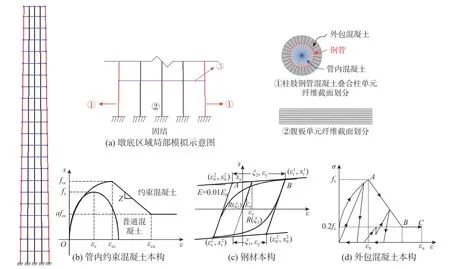
图6 基于纤维梁柱单元的CFST箱形叠合墩有限元模型Fig.6 Finite element model of CFSTRC-HBS pier based on fiber beam-column element

2.2 计算参数设置

采用集中质量法计算结构的自振频率，桥墩质量施加在相应的节点上。为了简化建模并提高计算效率，忽略桥墩中横撑、斜撑、风撑和横隔板等构造，但将相应的质量施加到节点上，同时考虑墩柱的P-Δ效应。进行时程分析时，采用通过施加在墩顶的轴力考虑上部结构的恒载作用，数值计算方法采用Newmark法，其中γ=0.5，β=0.25。采用瑞利阻尼，质量因子和刚度因子分别为0.062和0.038，阻尼比取0.05。

3 振动台试验结果与分析

3.1 基本动力特性分析

图7示出了白噪声扫描得到的墩顶加速度时程曲线频谱分析结果，得到试验缩尺模型的面外一阶基频为4.85 Hz，面内一阶基频为9.70 Hz。实桥原型桥墩的模态通过第2节建立的有限元模型计算得到。由表5可知，缩尺试验模型与原型桥墩的面外一阶基频比值为5.98∶1，面内一阶基频比值为6.10∶1，与理论频率相似比5.75∶1较为接近，误差在7%以内，基本验证了振动台缩尺模型设计的正确性。横、纵桥向输入地震波的时间压缩比例确定为1∶6。

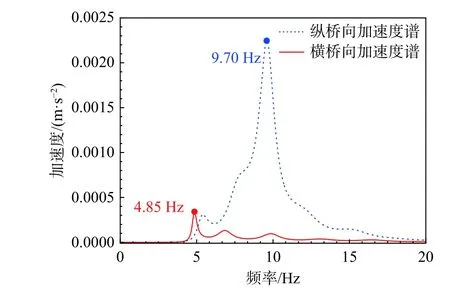
图7 白噪声激励下加速度频谱图Fig.7 Acceleration spectrum under white noise excitation

表5 试验缩尺模型与原型桥墩的模态对比Table5 Modal comparison between specimen and prototype

3.2 E2人工地震波作用下的桥墩响应

采用1∶6的时间压缩比，选取1.4节所述7条E2人工地震波分别在横桥向和纵桥向对试验模型进行激励，得到墩顶位移、墩顶加速度和墩底应变响应峰值，分别列于表6和表7。因为试验模型的纵桥向抗推刚度远大于横桥向抗推刚度，由表6和表7可知，相同E2人工地震波作用下，横桥向地震激励工况的墩顶位移响应、加速度响应和墩底应变平均约为纵桥向地震激励工况结果的3.6倍、1.4倍和1.6倍，说明本次振动台试验横桥向为模型最不利受力方向。

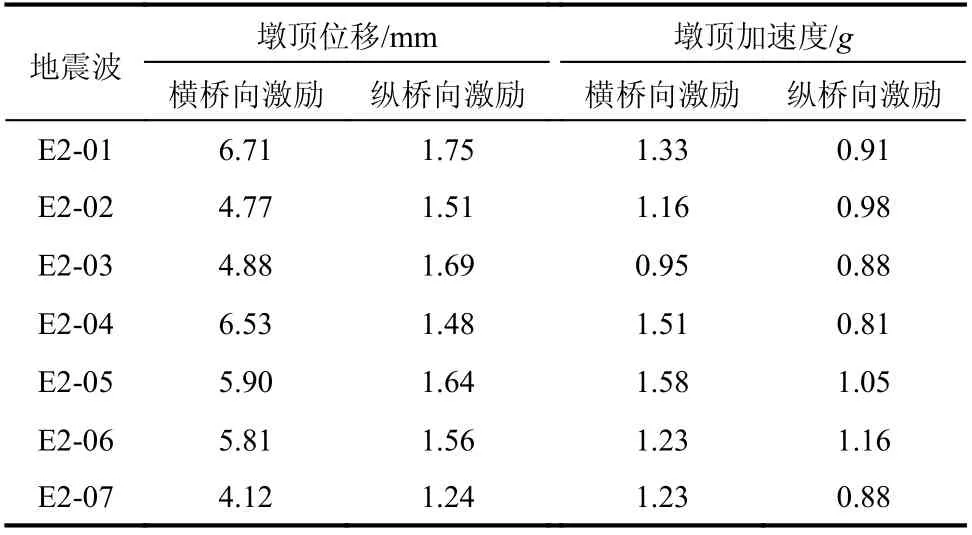
表6 E2地震作用下墩顶位移和加速度响应峰值Table6 Peak value of displacement and acceleration response under E2 earthquake

表7 E2水平地震作用下墩底截面应变响应峰值Table7 Peak strain response at pier bottom under E2 earthquake

限于篇幅，本节仅给出缩尺试验模型在E2-01人工地震波作用下的墩顶横桥向和纵桥向位移时程曲线，以及墩底截面应变的时程曲线，分别如图8和图9所示，同时图中也用虚线将E2地震作用下原型桥墩的有限元计算结果示出。

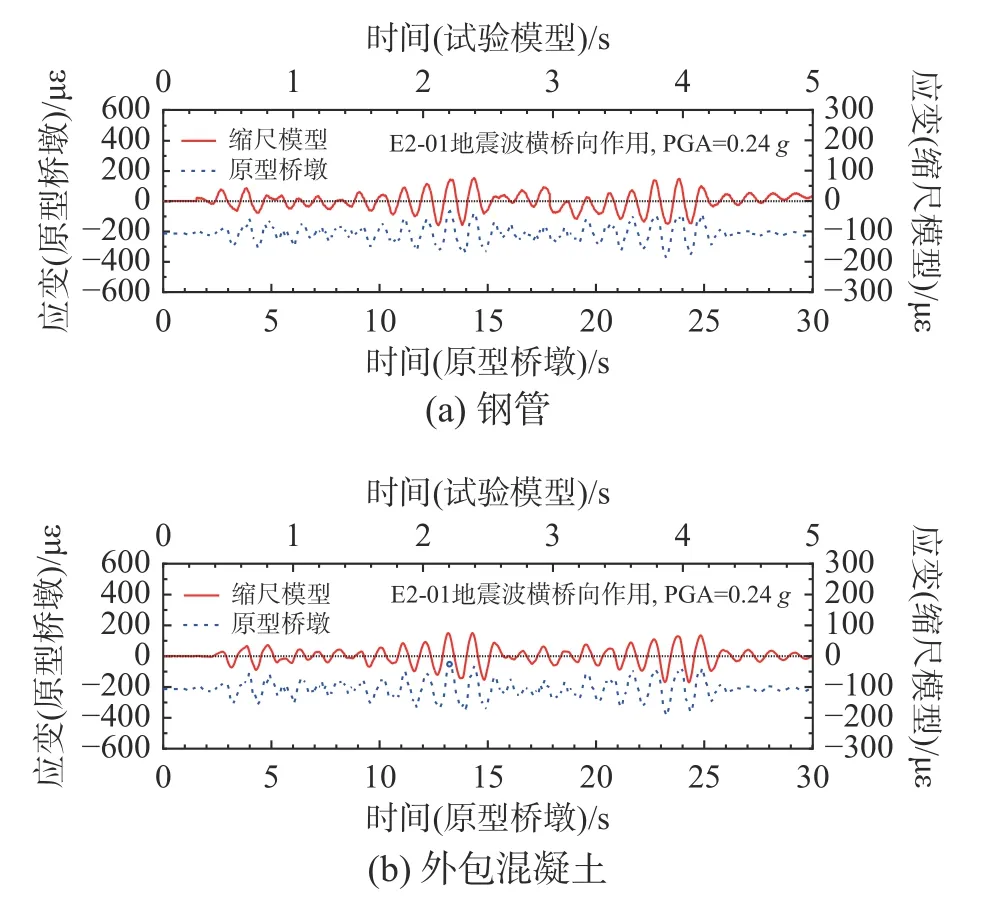
图9 E2水平地震作用下墩底应变时程曲线Fig.9 Strain response time history at pier bottom under E2-level earthquake

在E2人工地震波激励下：一方面，图8中缩尺模型和原型桥墩的墩顶位移近似满足表3中位移相似比(1∶)的关系，且两者时程曲线形状吻合较好；另一方面，由于应变传感器是在缩尺模型制作完成后才进行布置，导致无法测得自重作用下缩尺模型的初始应变，而原型桥墩有限元模型考虑了上部结构和墩身的自重作用，得到墩底截面初始应变为−213 µε。此外，受限于振动台的承载能力，本次试验仅能对缩尺模型进行欠配重设计，导致缩尺模型与原型桥墩的墩底截面初始应变相差较大，但图9中缩尺模型在地震作用下的应变增量时程图形与原型桥墩的应变时程图形吻合较好，且两者应变近似满足表3中应变相似比的关系。

由图9还可看出原型桥墩和缩尺模型的钢管最大应变均小于屈服应变，原型桥墩外包混凝土始终处于受压状态；缩尺模型外包混凝土的拉应变增量可达到81 µε，但受到缩尺模型自重及附加质量作用的影响，整个试验过程中缩尺模型截面大部分处于受压状态，墩身表面未发现裂缝，结构处于弹性工作状态。

综上所述，对振动台输入持时按照1∶6压缩的地震波，得到的缩尺模型地震响应可比较准确地反映原型桥墩的地震响应特性，同时缩尺模型试验结果也验证了基于纤维梁柱单元模拟CFST箱形叠合墩的有限元模型的准确性。由于受到振动台试验能力的限制，本文在第4节将采用原型桥墩的有限元模型进一步开展地震破坏机理分析。

3.3 地震动特性对地震响应的影响

为探讨地震动特性对CFST箱形叠合墩地震响应的影响，在完成E2人工地震波工况后，选择图5的9条典型地震波整体压缩至PGA=0.05 g并沿缩尺试验模型的横桥向进行激励，得到不同地震波作用下缩尺试验模型墩顶位移时程响应如图10所示，墩顶位移、墩顶加速度和墩底应变的响应峰值汇总于表8。

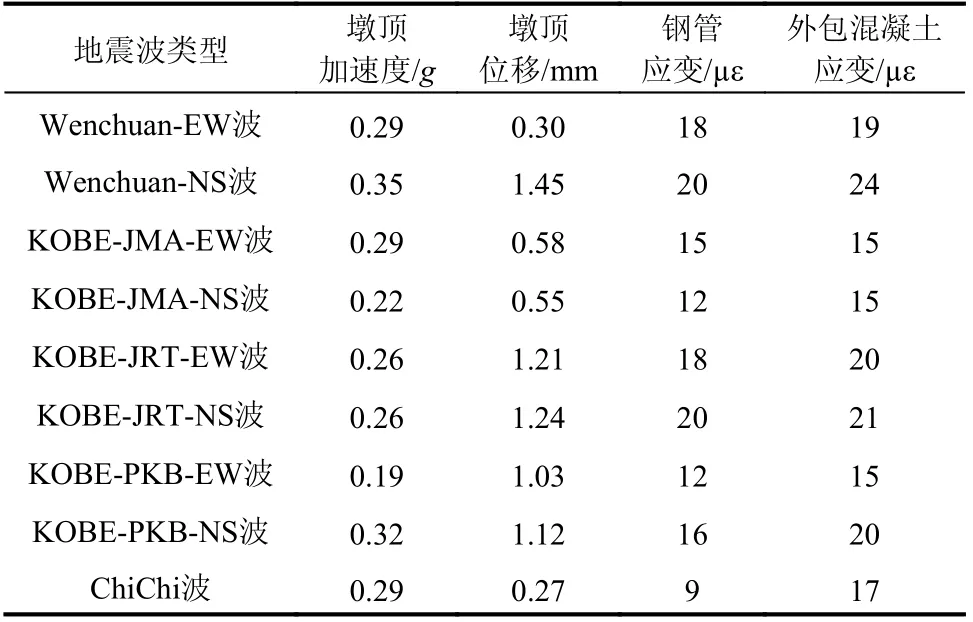
表8 典型地震波作用下结构响应峰值汇总表Table8 Summary of the maximum structural response under different earthquake actions

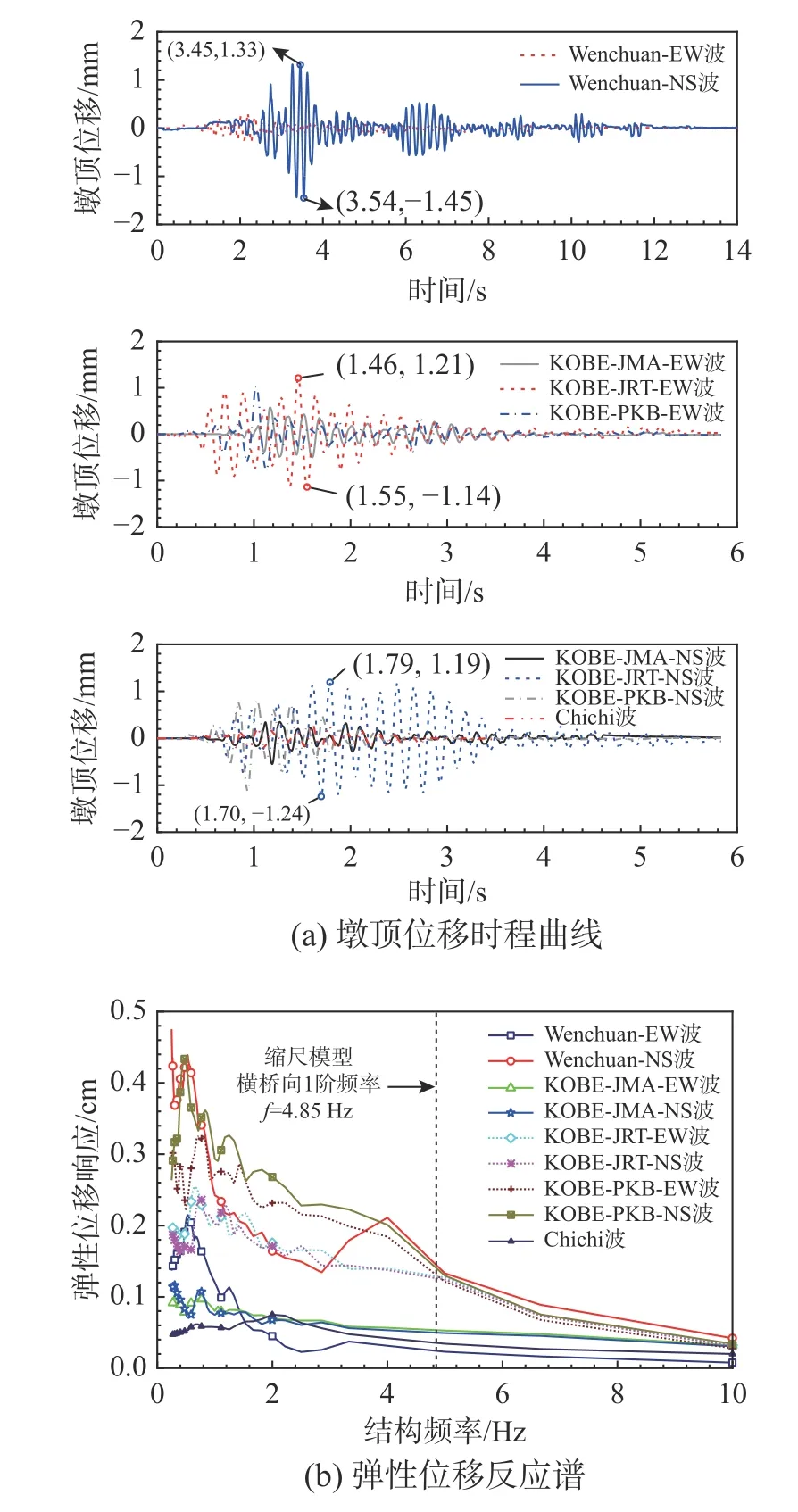
图10 典型地震波作用下墩顶位移响应分析Fig.10 Displacement response analysis of pier top under typical seismic waves

在选择的9条PGA=0.05 g的地震波作用下，KOBE-PKB-EW地震波作用下墩顶加速度响应最小(0.19 g)，Chichi地震波作用下墩顶位移响应最小(0.27 mm)；而在Wenchuan-NS地震波作用下，墩顶加速度响应和墩顶位移响应均达到最大(0.35 g和1.45 mm)，分别为KOBE-PKB-EW波和Chichi波结果的1.8倍和5.4倍。图10(b)绘制了PGA=0.05 g的各条地震波按1∶6时间比例压缩后得到的弹性位移反应谱。由图10(b)可知，对应于缩尺模型的面外1阶基频4.85 Hz，Wenchuan-NS波、KOBEJRT-NS波、KOBE-JRT-EW波等地震波的弹性位移响应数值较大，这与图10(a)中表现出幅度较大墩顶位移时程响应的地震波相符，表明上述地震波均含有激起缩尺模型共振的频率成分，其中以Wenchuan-NS波为最，说明地震动特性对CFST箱形叠合墩的地震响应有显著影响。

3.4 地震动强度对地震响应的影响

根据3.3节结果，选择Wenchuan-NS地震波按照0.05 g的增量逐级对模型进行激励，以探究地震动强度对CFST箱形叠合墩地震响应的影响。由于缩尺试验模型高度较高，当输入地震波的PGA超过0.35 g时，振动台承受的力矩超过其抗倾覆力矩，无法继续加载。

图11和图12分别为不同强度地震动激励下试验模型的墩顶加速度、墩顶位移时程曲线和响应峰值。可以看出，墩顶加速度响应和位移响应随地震动强度增大几乎呈线形增大，墩顶加速度出现了明显的放大现象；将墩顶加速度响应与台面输出加速度的比值定义为墩顶动力放大系数，由图可知随着Wenchuan-NS地震动强度的增大，由于试验模型始终处于弹性工作状态，其墩顶动力放大系数基本保持在6左右。

图 11 不同强度地震动作用下墩顶响应时程曲线Fig.11 Time history curve of pier top under different intensities of ground motion

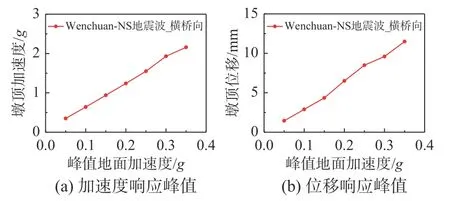
图12 墩顶响应峰值随地震动强度变化趋势图Fig.12 Trend chart of peak response of pier top along with intensity of ground motion

图13和图14分别为不同强度地震动激励下缩尺试验模型墩底钢管和外包混凝土的应变增量时程曲线和应变增量峰值。由图可知，墩底钢管和外包混凝土的应变增量峰值随地震动强度增大而线性增大，当Wenchuan-NS地震波的PGA增加到0.35 g时，墩底钢管最大拉应变增量为89 µε，最大压应变增量为−98 µε，墩底外包混凝土最大拉应变增量为95 µε，最大压应变增量为−101 µε。考虑到试验模型自重产生的初始应变，整个试验过程中缩尺试验模型墩底截面大部分处于受压状态，外包混凝土应变小于C30混凝土极限拉应变，墩身表面未发现裂缝，结构保持弹性工作状态。图14(b)绘制了墩底截面的应变分布情况，可以看出CFST箱形叠合墩试验缩尺模型的截面应变分布满足平截面假定，地震作用下外包混凝土、钢管和混凝土腹板变形协调，说明各组成部分的协同工作性能良好。

图13 不同强度地震动作用下墩底应变时程曲线Fig.13 Strain time-history curves at pier bottom under different intensities of ground motion

4 原型桥墩的非线性地震响应分析

4.1 单向地震作用下桥墩非线性地震响应分析

为进一步探究CFST箱形叠合墩在强震作用下的非线性响应特性和破坏模式，采用第2节提出的有限元建模分析方法，建立腊八斤特大桥11号主墩的有限元模型，并考虑上部主梁和墩身的自重作用，同时沿横桥向以0.05 g增幅输入Wenchuan-NS地震波，进行原型桥墩的非线性时程响应分析。限于篇幅，本文仅给出PGA=0.75 g时原型桥墩墩顶位移时程曲线和墩底剪力时程曲线。如图15所示，当PGA=0.75 g时，墩顶最大位移为928 mm(t=22.58 s)，墩底最大剪力为14 966 kN (t=23.12 s)，墩顶位移和墩底剪力达到峰值的时刻十分接近。

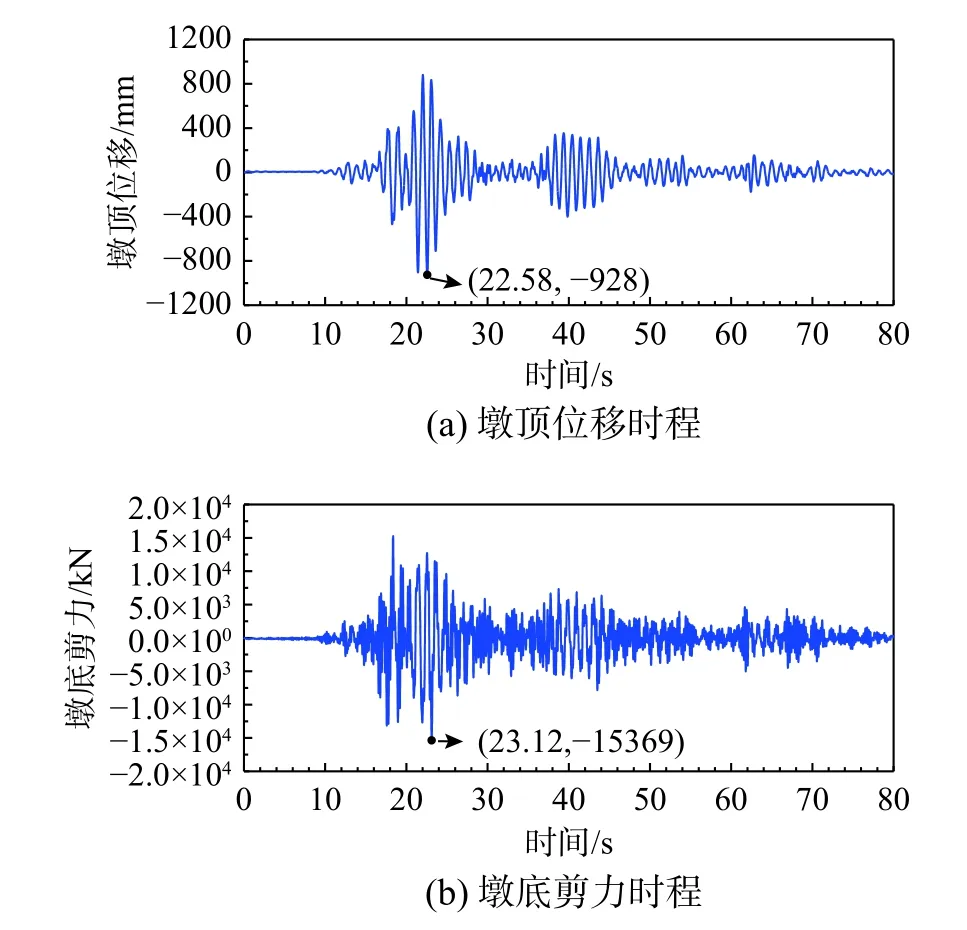
图15 PGA=0.75 g地震动作用下原型桥墩地震响应Fig.15 Seismic response of prototype bridge pier under PGA=0.75 g ground motion

图16绘制了墩顶位移响应峰值和墩底应变响应峰值随输入地震动PGA变化的趋势图。由图16可知，当PGA=0.30 g时，原型桥墩墩底截面外包混凝土最大拉应变为186 µε，超过了C30混凝土的极限拉应变(100 µε)，混凝土发生开裂。当PGA=0.75 g时，墩底截面钢管应变达到1684 µε，发生屈服；外包混凝土最大压应变为−1683 µε，未达到混凝土的压溃应变(−3300 µε)，还可以继续承载。此时墩身不同高度处应变响应峰值的分布如图17所示。可知横桥向地震作用下CFST箱形叠合墩的钢管和外包混凝土应变均由墩顶向墩底增大，墩底处钢管最先出现屈服，塑性铰出现在墩底区域。

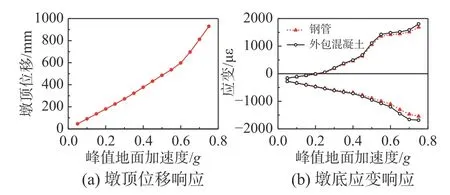
图16 原型桥墩响应峰值随地震动强度变化趋势图Fig.16 Trend chart of peak response of prototype bridge pier along with intensity of ground motion

图17 PGA=0.75 g地震动作用下原型桥墩应变分布图Fig.17 Strain distribution diagram of prototype bridge pier under PGA=0.75 g ground motion

4.2 双向地震作用下桥墩非线性地震响应分析

为研究双向地震作用对CFST箱形叠合墩地震响应的影响，先分别沿横桥向和纵桥向输入Wenchuan-NS地震波(PGA=0.59 g)和Wenchuan-EW地震波(PGA=0.65 g)，然后再双向(横桥向+纵桥向)同时输入地震波，比较单向地震和双向地震作用下原型桥墩非线性地震响应结果的差异。图18比较了单、双向地震作用下原型桥墩墩顶位移时程曲线，其中图18(a)比较了横桥向输入Wenchuan-NS地震波时的墩顶位移响应，图18(b)为纵桥向输入Wenchuan-EW地震波时的结果，图18(c)则比较了从墩顶上部俯视时的位移轨迹。表9对比了两种情况下的响应峰值。

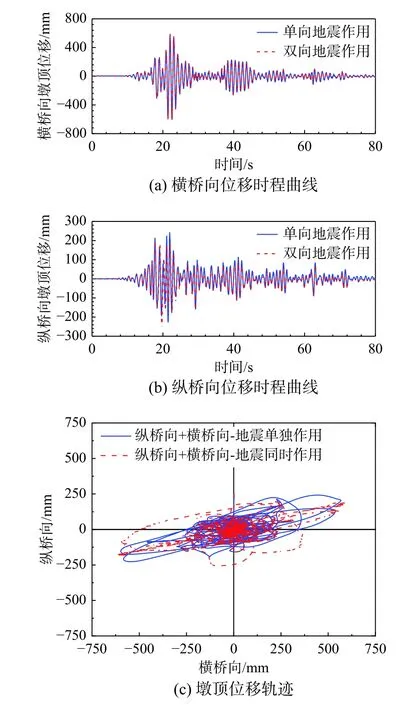
图18 单、双向地震作用下原型桥墩墩顶位移响应对比Fig.18 Comparison of displacement response of prototype piers under unilateral and bilateral earthquakes

由图18和表9可知，由于结构横桥向和纵桥向抗推刚度的显著差异，双向地震同时作用下原型桥墩的位移轨迹以横桥向为主振方向，且相比在横桥向和纵桥向单独输入地震激励，墩顶横桥向和纵桥向的最大位移响应分别增大了约4%和6%；与之相应，墩底横桥向和纵桥向的最大剪力分别增加了约2%和4%，最大弯矩均增加了约1%。以上结果表明与单向地震动作用相比，双向地震作用下CFST箱形叠合墩的结构响应变化不大，内力最大变化量仅为4%，因此，在进行CFST箱型叠合墩的抗震分析时，可只沿纵桥向和横桥向分别输入水平地震动。

表9 单向与双向地震作用下原型桥墩地震响应对比Table9 Comparison of seismic response of prototype bridge piers under unilateral and bilateral earthquakes

5 结论

本文以腊八斤特大桥11号主墩为原型，开展了CFST箱形叠合墩振动台缩尺模型的设计与试验，同时基于OpenSEES软件平台建立了采用纤维单元的空间杆系非线性有限元模型，进行强震作用下非线性地震响应分析，得到主要结论如下：

(1)缩尺试验模型与原型桥墩的横桥向一阶基频比值为5.98∶1，纵桥向一阶基频比值为6.10∶1，与理论频率相似比5.75∶1的误差在7%以内，验证了本文设计的振动台缩尺模型的正确性。

(2)采用基于纤维梁柱单元模拟钢管混凝土叠合柱肢和钢筋混凝土腹板、并通过弹性梁柱单元连接柱肢和腹板的有限元建模方法能比较准确地反映CFST箱形叠合墩的动力特征和地震响应特性，可用于实际工程中此类组合桥墩的抗震分析。

(3)E2罕遇地震设计地震动作用下，CFST箱形叠合墩表现出良好的抗震性能。墩底塑性铰截面大部分处于受压状态，墩身表面未发现裂缝，结构处于弹性工作状态。外包混凝土、钢管和混凝土腹板变形协调，各组成部分的协同工作性能良好。

(4)地震动特性尤其是地震动中含有激起桥墩共振频率成分的多寡对CFST箱形叠合墩的地震响应有较大影响。在保持输入地震波具有相同PGA的前提下，墩顶加速度和位移最大响应工况的数值可分别为最小地震响应工况的1.8倍和5.4倍，说明在进行CFST箱形叠合墩的抗震分析时应尽可能选择多组地震波以充分反映结构地震响应的特性。

(5)CFST箱形叠合墩的墩顶加速度响应、墩顶位移响应、墩底钢管和外包混凝土的应变响应随着地震动强度的增加基本呈线性增加；墩顶加速度动力放大系数约为6，且随着地震动强度的增大基本保持不变。

(6)横桥向地震作用下，CFST箱形叠合墩的钢管和外包混凝土应变均由墩顶向墩底增大，墩底截面的外包混凝土最先发生开裂，接着钢管出现屈服，塑性铰出现在墩底区域。

(7)相比纵桥向和横桥向地震单独作用，纵桥向和横桥向地震同时作用对CFST箱形叠合墩的地震响应影响较小，墩顶位移响应与墩底最大水平剪力仅分别增大约6%和4%，说明在进行CFST箱形叠合墩的抗震分析时，可分别考虑只沿纵桥向和横桥向输入水平地震动。