现代有轨电车线路扣件系统模态与钢轨波磨关系研究

张 昭，杨新文，马骙骙，赵治钧，陆文学

(1.同济大学轨道交通结构耐久与系统安全上海市重点实验室，上海 201804；2.同济大学道路与交通工程教育部重点实验室，上海 201804；3.苏州市轨道交通集团有限公司，江苏，苏州 215004)

现代有 轨电车具有节能、环保、投资少、易建设、景观效果好等优点[1]，截至2020年6月30日，中国内地累计17个城市投运现代有轨电车线路共429.93 km，占城市轨道交通运营总里程的6.21%[2]。出于路权共享的考虑，现代有轨电车路基段多采用嵌入式轨道[3]，随着运营时间的增加，由此产生的路面开裂、轨面沉降、棱边破损等病害[4]以及扣件罩破损、弹条断裂、轨下垫板失效等隐蔽病害，这些病害将会对行车平稳性与安全性、轨道及路面的寿命造成不利影响。

钢轨波磨是轮轨系统中常见的一种损伤，在不同铁路运输系统中均有出现。现代有轨电车线路上的钢轨波磨多是短波长波磨(波长25 mm～80 mm)[5]，如图1所示，出现在绿化与路基线路的曲线段和上坡段。现代有轨电车的运行速度可在30 km/h～70 km/h变化，通过短波波磨区段时，会引起车辆-轨道系统的中高频振动，列车通过频率与弹条固有频率接近时，弹条振动加剧，易产生振动疲劳[6]，导致弹条扣压力下降，甚至造成弹条疲劳断裂。

图1 有轨电车线路槽型轨波磨Fig.1 Groove rail corrugation of tram lines

弹条疲劳断裂现象在地铁线路中出现较多，这一病害在北京地铁及深圳地铁线路中均有出现。针对弹条破坏机理，为了准确分析弹条在安装状态及工作状态下的力学特性，钢轨-扣件系统精细化有限元模型被广泛应用于相关研究中[7−9]。诸多学者通过对钢轨-扣件系统进行动力学分析及现场测试[10−11]，研究弹条的动力响应及疲劳特性[12]，验证了弹条振动疲劳是弹条破坏的主要原因之一。

王平等[6]通过对深圳地铁有无波磨区段的弹条振动加速度进行现场测试，分析弹条振动的时频特性，并建立扣件系统振动疲劳模型，得出当列车通过频率与弹条固有频率吻合时，会降低弹条的疲劳寿命，验证了振动疲劳理论在轨道交通扣件系统弹条疲劳断裂机理领域应用的可能性。尚红霞等[13]通过有限元方法，表明Ⅲ型弹条断裂与安装状态有很大关联，随着弹条发生疲劳断裂，会导致轮轨作用力加剧，加速其他结构破坏。

国内外现有研究多基于发生弹条断裂的实际工程问题进行破坏机理与结构动力响应分析，缺乏对于弹条固有频率、列车通过速度、波磨波长等相关因素的系统分析及弹条振动疲劳破坏发生的预防措施研究。

目前，在现代有轨电车线路中仍未出现弹条断裂的现象，这是由于相较地铁线路，现代有轨电车的运量小、累积运营时间短、运行时间间隔大，因此弹条断裂这种极端病害还未出现，但随着运营时间的增加，一旦在有轨电车嵌入式轨道区段发生弹条断裂病害，则会带来病害检测不便、维修成本高、影响行车安全等诸多不利，所以对弹条断裂的发生原因的系统分析及预防是有必要的。

本文主要研究由振动疲劳机理引起的弹条断裂问题，利用ANSYS有限元分析软件建立现代有轨电车钢轨-扣件系统精细化模型，进行考虑安装预应力的模态分析，得出钢轨-扣件系统在不同轨下刚度下的弹条固有频率及可能破坏形式，再与列车通过频率做统计对比分析，确定弹条破坏出现对应的列车速度及波磨波长匹配关系，以期为现代有轨电车系统弹条振动疲劳断裂的预防及检测提供建议。

1 现代有轨电车扣件系统

1.1 YGⅠ-1扣件系统

YGⅠ-1扣件(图2)为无螺栓弹性分开式扣件，适用于有轨电车系统整体道床线路，所采用的弹条为“e”型弹条，直径为16 mm。

图2 YGⅠ-1扣件系统组装图Fig.2 Assembly drawing of YGⅠ-1 fastener system

1.2 典型弹条断裂形式

“e”型弹条包括中肢、小圆弧、跟端、大圆弧和趾端5个部分，通过对地铁线路“e”型弹条断裂的现场观察[14−15]，典型弹条断裂形式如图3所示，主要有小圆弧近中肢处(图3(a))、小圆弧近跟端处(图3(b))、大圆弧近跟端处(图3(c))3种断裂形式。

图3 “e”型弹条典型断裂形式图Fig.3 Typical fracture type diagram of "e"type rail clip

现代有轨电车线路中虽无弹条断裂病害发生，但对于同样采用“e”型弹条的YGⅠ-1扣件系统，弹条在车辆-轨道系统中受力情况与地铁线路中相似，故以地铁线路中弹条典型断裂形式作为有轨电车线路可能发生的弹条断裂形式。

2 有限元模型

利用ANSYS有限元软件建立钢轨-扣件系统精细化模型如图4所示。YGⅠ-1扣件系统零部件较多，本文主要在考虑安装预应力条件下对弹条进行模态分析，简化螺旋道钉、尼龙套管及扣件罩等对分析影响较小的部件，并通过施加相应的约束来等效替代其限位、固定的功能。模型包括槽型轨、轨下垫板、轨距块、弹条及铁垫板5个部分，其中弹条采用四面体单元网格，其余部件采用六面体单元网格，模型建立如图4(a)所示，扣件间距为0.6 m。

在扣件系统安装中，各部件之间的接触状态随着结构受力变化也发生改变，产生的非线性接触问题需要通过设置合适的接触单元来模拟。各组接触对之间采用面-面接触，轨距块的主要作用是保持轨距，对钢轨有水平限位作用，设置为粗糙接触模式。其余部件之间均为摩擦接触，金属材料与金属材料之间的摩擦系数取0.15，与非金属材料之间的摩擦系数取0.8。弹条中肢固定约束处理，其根部距圆孔端10 mm，弹条趾端下表面与轨距块上表面、弹条跟端下表面与铁垫板上表面均存在接触，如图4(b)所示。

图4 钢轨-扣件系统有限元模型Fig.4 Finite element model of rail fastener system

弹条材料为60Si2MnA弹簧钢，考虑到弹条在安装时局部位置会发生塑性变形，弹条材料的应力-应变关系采用理想线性强化弹塑性材料本构模型，强化模量可设置为 E′=0.1E[16]，下屈服强度为1375 MPa，抗拉强度为1570 MPa，可得如图5所示双线性等向强化模型。其中轨下垫板刚度弹性模量随刚度变化如表1所示，模型各部件所用材料参数见表2。

表1 轨下垫板弹性模量Table1 Elastic modulus of rail pad

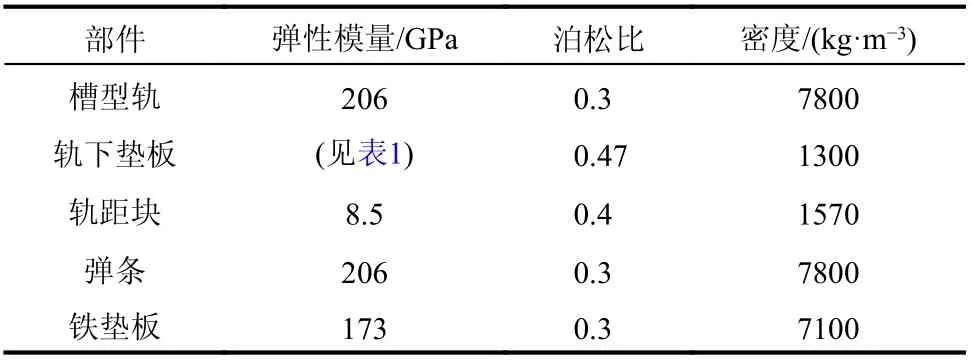
表2 材料参数Table2 Material parameters

图5 弹条材料本构模型Fig.5 The constitutive model of rail clip material

3 扣件系统模态分析

模态分析是将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程。

弹条在自由状态及安装状态下所对应的模态固有频率有所不同，在钢轨-扣件系统中，考虑安装预应力，可以更加真实地反映弹条的在不同模态固有频率下的等效应力分布情况，按照图6所示分析流程进行后续模态分析。

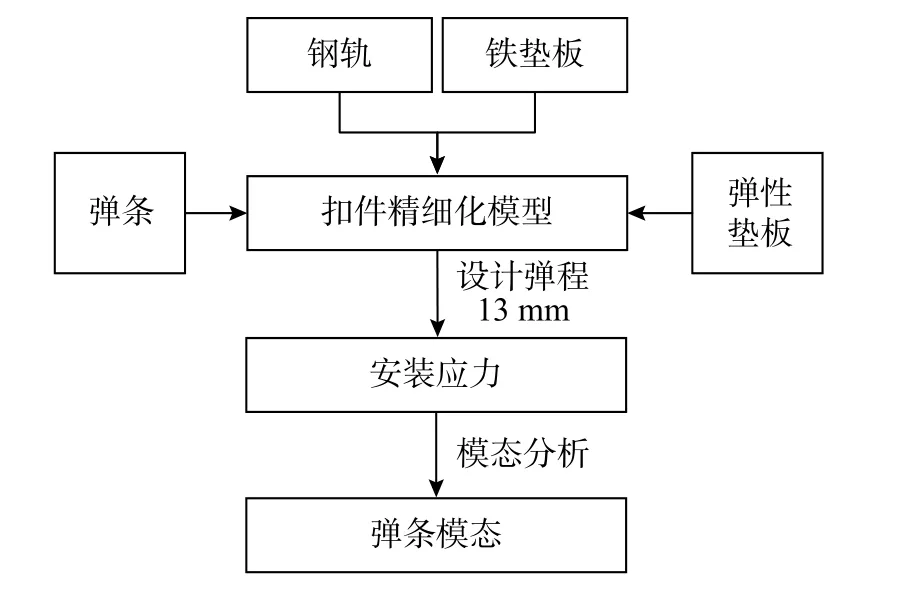
图6 扣件系统模态分析流程Fig.6 Modal analysis of fastener system

3.1 自由状态下弹条模态分析

对自由状态下的弹条有限元模型进行模态分析，为了涵盖图3所示的典型弹条断裂形式，对弹条前4阶模态进行分析，得到相应的等效应力分布云图如图7所示。其中，弹条第1阶和第2阶模态(图7(a)、图7(b))使得弹条小圆弧近跟端a处等效应力较大，易发生振动疲劳断裂，模态固有频率分别为732.93 Hz、747.35 Hz；弹条第3阶模态(图7(c))对应小圆弧近中肢b处疲劳断裂形式，模态固有频率为1023.7 Hz；弹条第4阶模态(图7(d))对应大圆弧近跟端c处疲劳断裂形式，模态固有频率为1362.7 Hz。

图7 自由状态下弹条模态振型等效应力分布Fig.7 The equivalent stress distribution of rail clip under free state

自由状态下弹条前4阶模态振型的等效应力分布可与3种典型弹条破坏形式对应，但在有轨电车线路中，波磨区段的列车通过频率一般在1000 Hz以下，则自由状态下弹条模态对应的固有频率不能很好地解释小圆弧a处及大圆弧c处的断裂原因，仍需通过施加约束，来更加真实地反映弹条在钢轨-扣件系统中的受力特点及模态固有频率。

3.2 安装状态下弹条模态分析

在实际安装中要求弹条小圆弧内层与铁垫板端部的距离保持在8 mm～10 mm[13]，本文取10 mm。YGⅠ-1扣件中弹条设计弹程为13 mm，通过施加位移荷载模拟弹条安装过程，按照图6所示流程进行考虑安装预应力的钢轨-扣件系统模态分析，通过观察对比槽型轨内外侧弹条各阶模态的等效应力分布情况，将典型弹条断裂形式与弹条前20阶模态对应，3种典型断裂形式对应的弹条模态等效应力分布如图8所示，断裂形式与模态阶数对应关系汇总结果见表3。

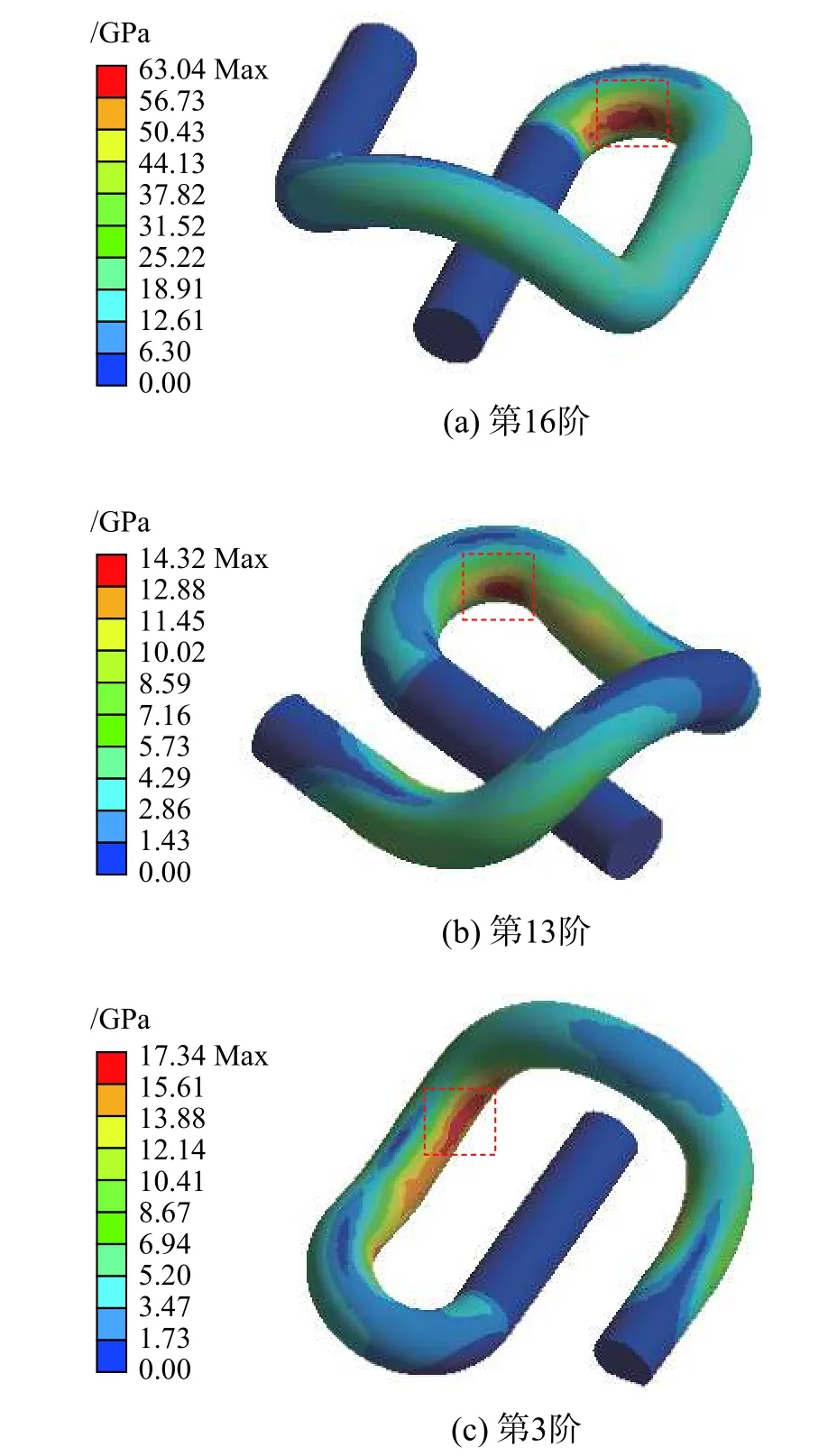
图8 安装状态下弹条模态振型等效应力分布Fig.8 The equivalent stress distribution of rail clip under installation state

由表3可知，在钢轨-扣件系统中，内、外侧弹条在不同阶数的模态振型下，表现出不同模态的等效应力分布情况，即同一阶模态下，内、外侧弹条对应不同的典型断裂形式。小圆弧a、b处断裂多是由10阶以上模态引起的振动疲劳损伤导致，而大圆弧c处断裂则对应10阶以下模态。

表3 典型弹条断裂形式对应模态阶数结果汇总Table3 Results of mode order corresponding to typical fracture type of elastic bar

3.3 轨下垫板刚度变化对弹条模态的影响分析

扣件系统轨下垫板刚度对弹条特定阶数的模态固有频率会有一定影响，因此，对不同轨下垫板刚度下的扣件系统进行模态分析，探究不同断裂形式对应弹条模态受轨下刚度影响的程度，是有必要的。本文取轨下垫板刚度为20 kN/mm～50 kN/mm，对应轨下垫板材料参数见表1和表2。将弹条前20阶模态固有频率与典型断裂形式对应关系表示如图9所示。

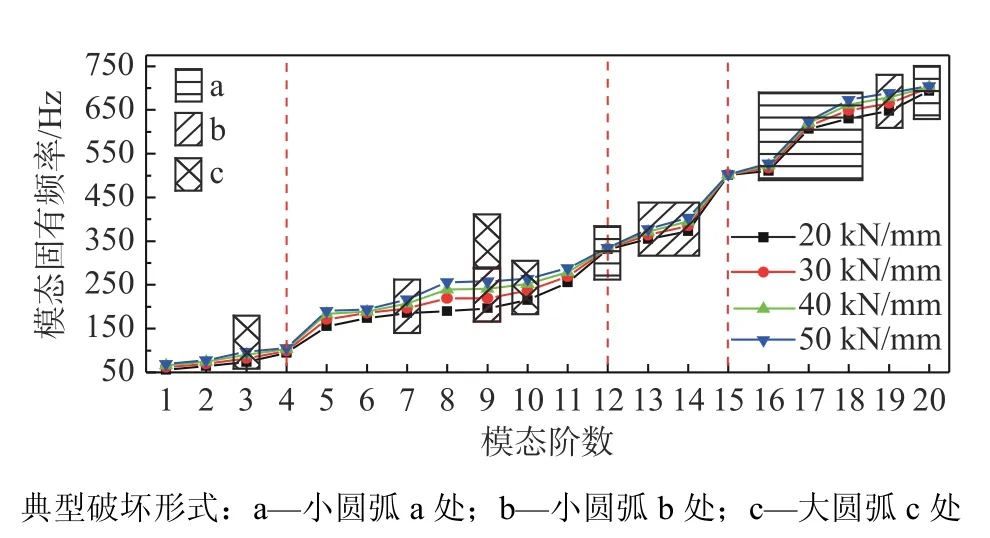
图9 轨下垫板刚度变化对弹条模态固有频率的影响Fig.9 Influence of the rail pad stiffness change on modal natural frequency of rail clip

由图9可知，随着轨下垫板刚度的增大，弹条的安装初应力发生变化，导致弹条各阶模态固有频率都有一定程度的提高，最大提高约70 Hz。弹条第4阶、12阶和第15阶模态固有频率基本不受轨下垫板刚度变化的影响，而第8阶～10阶、18阶～19阶模态固有频率则受到较大影响。

小圆弧a处断裂形式对应弹条第12阶、16阶～18阶和第20阶模态，考虑到轨下垫板刚度变化，相应弹条模态固有频率范围为331.57 Hz～335.02 Hz、510.34 Hz～527.30 Hz、606.92 Hz～673.51 Hz、693.50 Hz～704.62 Hz，其中受轨下刚度影响较大的固有频率为630.16 Hz～673.51 Hz，对应弹条第18阶模态；小圆弧b处断裂受弹条第7阶、9阶、13～14阶和第19阶模态影响，相应的弹条固有频率为185.44 Hz～258.31 Hz、354.64 Hz～403.80 Hz、647.55 Hz～689.48 Hz，受轨下刚度影响较大的固有频率为196.64 Hz～258.31 Hz，对应外侧弹条第9阶模态；小圆弧c处断裂受弹条第3阶、9阶和第10阶模态影响，相应弹条模态固有频率分别为73.34 Hz～96.82 Hz和196.64 Hz～263.95 Hz，受轨下刚度影响较大固有频率为196.64 Hz～258.31 Hz，对应内侧弹条第9阶模态。

因此，增加扣件系统轨下垫板刚度会提高扣件系统中弹条的模态固有频率，弹条的3种典型破坏形式对应的模态均会受轨下垫板刚度变化的影响，在实际运营中，更换轨下垫板时，需要充分考虑垫板刚度并控制垫板刚度的变化范围。

4 现代有轨电车通过频率分析

扣件系统在外界列车通过时所激发的振动是引起弹条局部振动疲劳损伤的主要原因。影响列车通过频率的因素有多种，包括轨枕间距、固定轴距、车辆定距、全轴距、钢轨波磨等。对于现代有轨电车系统，当列车运行速度为30 km/h～70 km/h，钢 轨 短 波 波 磨 波 长 为25 mm～80 mm时，列车通过频率为：

式中：v为列车速度；λ为波磨波长。由式(1)计算可得列车在波磨区段的通过频率为104.2 Hz～777.8 Hz。

4.1 列车通过频率统计分析

按照1 km/h和1 mm的梯度离散列车运行速度及波磨波长，得到列车通过频率与运行速度、波磨波长之间的关系，如图10所示。由图可知，当有轨电车以45 mm～70 km/h的速度通过波长为25 mm～40 mm的钢轨波磨区段时，可产生500 Hz以上的高频段列车通过频率。

图10 列车通过频率与车速、波磨波长关系图Fig.10 Relation diagram between train passing frequency,speed and rail corrugation wavelength

对列车通过频率进行统计分析，可得其频率分布直方图与累计百分比如图11所示。在各种列车运行速度及波磨波长等概率分布的条件下，列车通过频率分布在500 Hz以下频段的累积频率超过90%，且在200 Hz左右频段出现的频率最高。考虑到有轨电车在实际运营中也是低速运行居多，列车通过波磨区段时所产生的通过频率主要分布在中低频段。

图11 列车通过频率直方图及累积百分比曲线Fig.11 Histogram and cumulative percentage curve of train passing frequency

4.2 列车通过频率与弹条模态关系分析

根据第3节结果，将各典型断裂形式对应的弹条模态频率以面积分布的形式建立和车速、波磨波长的对应关系，如图12所示。

由图12(a)～图12(c)可知，小圆弧a处断裂对应的弹条模态固有频率主要分布在中高频段，小圆弧b处断裂对应弹条模态在中低频及高频段均有分布，大圆弧c处断裂对应弹条模态则分布在中低频，在列车车速和钢轨波磨波长等概率分布时，3种典型弹条断裂出现的概率分别为3.5%、36.3%和25.9%。

图12 弹条模态频率与车速、波磨波长关系图Fig.12 Relation diagram of rail clip modal frequency with vehicle speed and rail corrugation wavelength

考虑实际有轨电车运营速度及波磨波长均分布在特定的范围，通过对图12的局部截取，即可获得实际中各断裂形式出现概率，结合脉冲激励下钢轨振动响应的扣件失效识别算法[17]，便于有针对性的检测。

由图13可得，受轨下垫板刚度影响较大的弹条模态固有频率频段分布于中低频及高频区域，其中，中低频区域主要对应小圆弧b处及大圆弧c处弹条断裂形式，高频区域对应小圆弧a处弹条断裂形式。

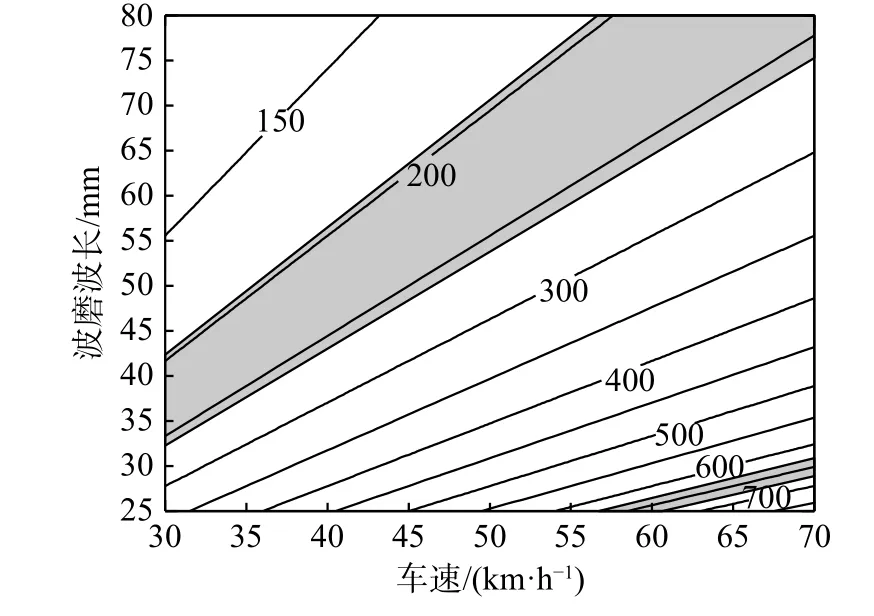
图13 考虑轨下垫板刚度影响弹条模态频率与车速、波磨 波长关系图Fig.13 Relation diagram of rail clip modal frequency,vehicle speed and rail corrugation wavelength considering the influence of the rail pad stiffness

当列车通过频率处于上述频段时，要考虑列车速度、波磨波长及轨下垫板刚度三者的匹配关系，尽可能避开相应的敏感频段，通过调整轨下垫板刚度、列车通过速度，实现最优的运营状态。

5 结论

本文通过建立钢轨-扣件系统精细化模型，对安装预应力下的扣件系统进行模态分析，并对列车通过频率进行分析，探究了弹条典型断裂形式、弹条模态、列车速度、波磨波长、轨下垫板刚度之间的关系，可以得到如下结论：

(1)弹条小圆弧处断裂与弹条中高阶模态引起的振动疲劳有关，大圆弧处断裂与弹条中低阶模态引起的振动疲劳有关。对于现代有轨电车系统，列车通过频率主要分布在500 Hz以下频段，需要重点关注弹条小圆弧近跟端及大圆弧近跟端处弹条的伤损情况，以避免弹条断裂的发生。

(2) 轨 下 垫 板 刚 度 在20 kN/mm～50 kN/mm范围内变化时，随着刚度增加，对应模态固有频率提高，其中，受轨下垫板刚度影响较大的频段为196.64 Hz～258.31 Hz、630.16 Hz～673.51 Hz，当列车通过频率处于上述频段时，需要综合考虑轨下垫板刚度、车速、波磨波长三者的匹配关系，从而有针对性地调整轨下垫板刚度及列车运营速度，预防有轨电车扣件系统的弹条断裂。

(3)考虑列车以30 km/h～70 km/h的速度通过波长为25 mm～80 mm的钢轨波磨区段时，在列车车速和钢轨波磨波长等概率分布的条件下，3种典型弹条断裂出现的概率分别为3.5%、36.3%和25.9%。在考虑有轨电车线路实际运营条件的基础上，可按照相同方法对指定的线路进行有弹条断裂形式出现概率预测，从而有针对性地安排线路养护维修及伤损检测等相关工作。