基于偶极子模型的双小行星系统平衡点特性研究

李 旭，钱霙婧，杨晓东，张 伟

(1. 北京工业大学材料与制造学部，北京 100124；2. 北京市非线性振动与机械结构强度重点实验室，北京 100124)

小行星是太阳系内类似行星环绕太阳运动，但体积和质量比行星小得多的天体。19世纪初，意大利天文学家Piazzi发现了第一颗小行星1 Ceres。截至2014年已经编目的小行星已近50万颗且在逐年增加，其中包括大量双小行星系统或多小行星系统[1]。1993年伽利略飞船在前往木星的路途中发现了Ida和它的卫星Dactyl，这是人类第一次发现的双小行星系统[2]。随着天文观测技术的不断提高和航天技术不断发展，比如太阳帆航天器被广泛应用于深空探测任务[3−4]，被发现的双小行星数量不断增加，据估计双小行星系统约占近地小行星总数的15%±4%[5]。近年来，双小行星探测已发展为未来探测任务的首选目标之一。欧洲航天局ESA(European Space Agency)提出的MarcoPolo-R任务中，将双小行星系统(175706) 1996 FG3的第二主星作为目标小行星进行着陆[6]。美国国家宇航局NASA(National Aeronautics and Space Administration)和欧洲ESA联合提出的小行星撞击和偏转评估任务(asteroid impact and deflection assessment,AIDA)对存在潜在危险的近地双小行星(65803)Didymos进行探测器撞击的测试，以评估验证近地小行星防御的可能性[7]。美国喷气推进实验室(JPL)提出双小行星(65803) Didymos定位探测(Binary asteroid in-situ explorer mission, BASIX)任务，拟计划对双小行星系统进行定量测量[8]。对双小行星系统的研究有助于了解太阳系中天体的形成和演化机理，具有独特科学价值及经济价值。而深入了解双小行星系统附近的动力学环境，则对轨道设计和控制策略至关重要，也是相关探测任务成功的关键和基础。

根据双小行星系统的旋转周期和形态，当系统的旋转周期和两颗小行星自转周期相同时，称为双同步双小行星系统(doubly synchronous system)。当两颗小行星的自转周期和系统旋转周期均不同时，称为异步双小行星系统(asynchronous system)，此时系统最为复杂。当一颗小行星自转和系统旋转周期一致时，称为单同步双小行星系统 (singly synchronous system)[9]，这种情况一般发生在大尺度比的双天体和多天体系统中。单同步和双同步双星是人类探测任务最有可能的目标，因为它们有稳定的状态、形态特征和丰富的动力学行为。

由于小行星的不规则形状，在其附近运行的探测器所受到的引力场非常复杂。建立合理的引力场模型是研究这些不规则小行星附近动力学的第一步。对于单个小行星的引力场建模问题，经历了从简单到复杂、从低维到高维的研究阶段。经典的引力场建模方法是级数展开法(series expansion method)[10]。对于近球形的小行星，球谐函数摄动展开方法具有良好的效果[11]。然而，大部分小行星为强不规则天体，表面附近Legendre级数难以收敛[12]。为了改进球谐函数法，Bierly[13]和MacMillan[14]提出椭球谐函数法。Romain等[15]对Wirtanen彗星的引力场运用椭球谐函数法进行建模并对着陆过程进行了模拟。为了进一步精确描述小天体不规则引力场，1993年Werner等[16]独立推导了均质多面体引力场建模方法。之后，Werner与Scheeres[17]合作改进了上述方法，并成功应用到小行星4769 Castalia引力场的建模。此外Geissler等[18]提出质点群法来近似小行星整体的引力场。然而，多面体法和质点群法的计算时间会随引入面元或点质量的数量而增加，而且很难分析动力学特性和模型参数(例如，形状尺寸参数、质量参数、自旋参数等)之间的关系，即很难通过参数变化探究得到某一类具有相似外形小行星引力场动力学特性。而简化模型法则能做到这一点，如细直棒模型[19−24]、偶极子模型[25−26]、双直棒模型[27]、圆环模型[28−29]、圆饼模型[30−32]、三角盘和正方形盘[33]、三粒子粒杆模型[34−35]、偶极子段模型[36]、立方体模型[37−39]、哑铃体模型[40 − 41]等。

双小行星系统被认为是由一颗小行星俘获附近的另一颗小行星或分裂演化而形成的[42−43]。为了简化双小行星系统，Wang等[44]采用圆形限制性三体模型(i.e. CRTBP)来描述双小行星附近的运动，提出一种捕获策略并将其运用到90 Antiope双小行星系统和216 Kleopatra小行星系统中。然而，当双小行星系统中两天体距离比较近，质量分布和形状强不规则时，两天体不能简单地视为两质量点，CRTBP模型也不再适用。为了准确地研究双星系统附近的轨道运动，研究者们努力发展适合描述航天器在双星系统重力场中的轨道运动的模型和方法。与单个小行星相似，双小行星系统中的天体也可以被合适地视为球体、椭球体或者不规则体。一些简化模型法被成功应用到双小行星系统中。Bellerose和Scheeres[45−46]研究了球—椭球双星系统的周期轨道，特别是平动点周期轨道。Chappaz和Howell[47]研究了球—椭球双星系统和椭球—椭球双星系统。Linder等[21]用细直棒和一个点质量来模拟双小行星系统中的主星和次星，并发现细直棒附近存在稳定的同步轨道、一般的混沌轨道、不稳定周期轨道、旋转稳定轨道等。Blaikie等[48]研究了2个细直棒组成的双小行星系统在相互影响下各自的轨道与姿态响应。Jain和Sinha[49−50]考虑两个细直棒在同步旋转状态下系统平衡点附近的动力学行为。Ferrari等[51]使用3个粒子模拟双小行星，用2个不同的三体系统构建模型，他们称该模型为拼接三体问题(patched three-body problem)。类似地，Torres Dos Santos等[52]将一个主小行星视为球体、将另一个不规则小行星视为旋转的质量偶极子去构建同步双小行星系统模型，并对系统的平衡点进行了分析。除了研究平动点周期轨道，双小行星系统的共振轨道也被研究和分析。杨雅迪等[53]基于双椭球模型，给出同步双小行星系统中共振轨道的设计方法并以双小行星系统1999 KW4为例设计了1∶1、1∶2、1∶3、1∶4、2∶3共振轨道族。Nadoushan和Assadian[54]假设2个小行星为一个球体和一个椭球体，研究了自旋-轨道共振，同时还计算了一个假定的双小行星系统的庞加莱截面。Shang等[55]基于轨道的对称性搜索了椭球—椭球双星系统的全局周期轨道，得到了不同的共振轨道族。

小行星平衡点的位置为进行长期科学观测提供了难得的有利条件。利用平衡点处的动力学特性，可以设计很多具有实际应用价值的轨道，对扩展探测任务的科学回报具有重要意义。一般国内外学者都是重点关注小行星自身平衡点的存在性、个数与稳定性问题。Elipe和Riaguas[56]计算了旋转对数函数并找到有限长细直棒引力场中的4个外部平衡点，同时讨论了这4个平衡点的线性稳定性。Scheeres等[57]发现了小行星25143 Itokawa引力场中的4个外部平衡点及相应的位置坐标。Mondelo等[58]计算了小行星4 Vesta引力场中的4个外部平衡点的坐标及稳定性；他们的研究表明，其中2个平衡点是稳定的，另外2个是不稳定的。Liu等[37]给出了当引力加速度与离心加速度之比为1时的旋转均质立方体引力场中的平衡点位置。Yu和Baoyin[59]基于多面体模型分析了小行星216 Kleopatra引力场中的4个外部平衡点及其局部流形，并给出了这些平衡点的位置坐标、特征值与稳定性。Scheeres[60]发现了小行星1580 Betulia引力场中的6个外部平衡点，以及彗星67P/CG引力场中的4个外部平衡点。Jiang等[61]建立了一般旋转不规则小天体引力场中平衡点附近的运动理论，根据特征方程的特征值的不同情况对小行星的平衡点进行了拓扑分类。之后Jiang[62]还讨论了小行星平衡点附近的周期轨道和平衡点的拓扑类型关系。Wang、Jiang和Gong[63]计算了23个强不规则小天体的平衡点的个数、分布情况及稳定性。Jiang等[64]还研究了22 Kalliope小行星的平衡点在自转速率和密度的影响下的运动。在动力学研究领域广泛应用的参数化分析方法[65−66]也适用于小行星平衡点相关特性的研究，比如Zeng等[36]建立偶极子段模型，参数化研究了系统平衡点的位置和稳定性变化趋势。这些工作对本文的平衡点动力学特性的研究具有一定的指导意义。

由文献可知，简化模型适合前期的定性分析，帮助理解或认识实际不规则的双小行星系统特性，且具有易于推导的引力势表达式，容易展开动力学特性分析。偶极子模型作为一种简化模型，其能够有效地近似细长类小行星引力场。文章针对主星是细长型的小行星，而次星是小而规则的天体的双小行星系统，建立了普适性的引力场模型。针对同步旋转情况，对系统的平动点特性进行研究，细致分析系统参数对同步双小行星系统平衡点的影响。在非同步情况下，给出了系统等效平衡点的运动规律。最后，结合路径搜索修正法与伪弧长延拓方法有效地计算得到共线平衡点附近的周期轨道族。本文的研究可以为未来这一类双小行星系统的探测提供参考。

1 双小行星系统动力学模型

本文关注主星是细长型的小行星，而次星是小而规则的天体的双小行星系统，并采用偶极子—粒子模型对系统进行描述，如图1所示。系统中，主小行星P12为细长型强不规则小行星，由2个偶极子P1和P2(质量分别是m1和m2)和一根长度固定为ld的无质量杆细杆构成[33]。主小行星P12绕其质心B匀速自转运动。次小行星P4为质点，其质量为m4，且m4＜ m1+ m2。质量点P1、P2和P4在同一平面内运动。主小行星P12质心和次小行星P4之间距离为h，且h＞ld。P3为探测器，其质量为m3，探测器运动对其他引力体不产生影响。在系统中，P1和P2到质心B的距离分别为d1和d2，且有ld= d1+ d2。P4到质心O的距离为s1，而主小行星质心B到系统质心O之间的距离为s2，h = s1+ s2。

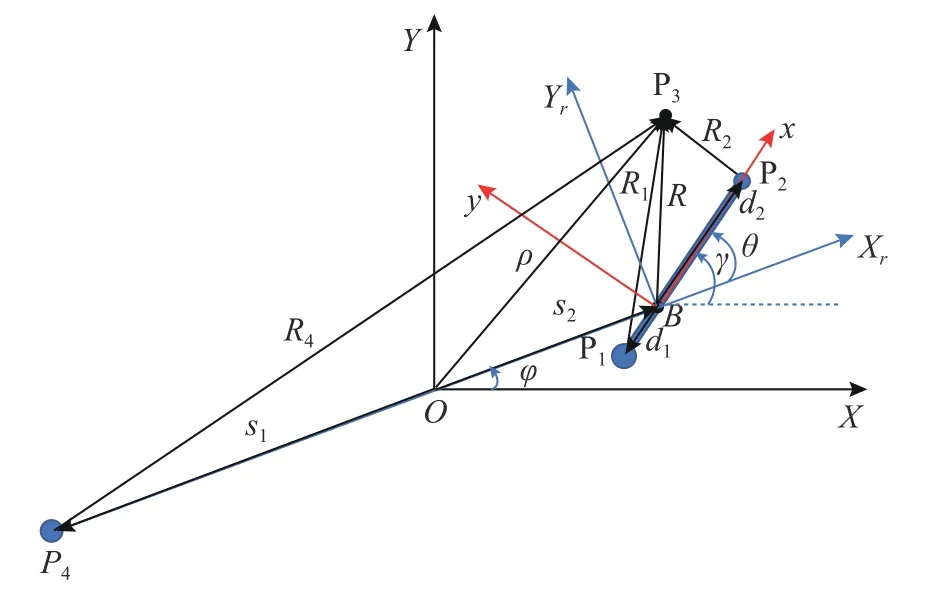
图1 双小行星系统简化模型示意图Fig. 1 The simplified model of binary asteroid

为方便描述，文中定义如下3个坐标系统：

1) 双小行星系统惯性坐标系(O-XYZ)：原点O是双小行星系统的质心；X-Y坐标面即两个小行星相对运动平面，X轴方向的选择，对应初始时刻t=t0时，两个小行星处于该坐标轴上，且正方向由系统质心O指向主小行星质心B，Z轴垂直于双小行星相对运动平面且和系统角动量方向一致；OY轴与另外两轴形成右手坐标系。

2) 系统旋转坐标系(B-XrYrZr)：原点B位于主小行星质心，该坐标系相对于O-XYZ坐标系的角速度为Ω1=φ˙Z，即两个小行星围绕系统质心系的运动角速度。Xr轴正方向由P4指向主小行星质心B。BZr轴和OZ轴平行且正方向一致，BYr轴与另外两轴形成右手坐标系。

3) 主小行星体坐标系(B-xyz)：原点B位于主小行星质心，该坐标系相对于O-XYZ坐标系的绝对自转角速度为Ω2=γ˙Z，Bx轴与偶极子段重合沿P1指向P2方向；Bz轴为自转轴且其正方向为主小行星自转角动量方向；By轴与另外两轴形成右手坐标系。此外，主小行星体坐标系(B-xyz)以角速度Ω=θ˙Zr相对于坐标系(B-XrYrZr)做匀速旋转运动。由于Zr和Z方向一致，Ω亦可表示为Ω=Z。根据模型描述易知，Ω2=Ω1+Ω。

在惯性系中，则探测器P3的加速度可表示为：

式中：Ri=‖Ri‖(i=1,2,3)表示探测器P3相对Pi的距离；ρ为探测器P3的位置矢量，可表达为：

式中，(x,y,z)是探测器P3在主小行星体坐标系中位置矢量R的坐标。对式(2)进行求导可得：

式中：上标“I”“rel”分别表示相对双小行星系统惯性坐标系和主小行星体坐标系进行求导。将对应的角速度Ω1、Ω2代入式(3)并求导，可得探测器P3的速度和加速度：

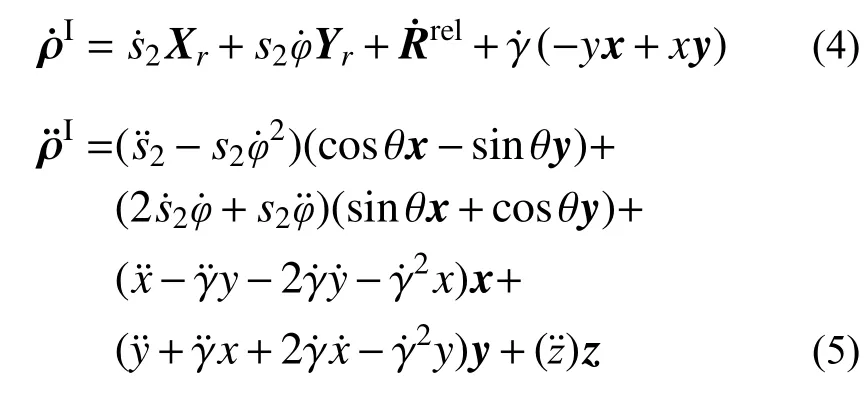
接下来，对于式(1)右边部分进行计算，将Ri(i=1,2,3)表示为：

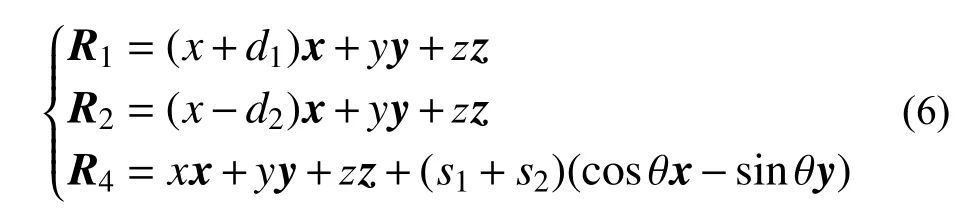
将式(6)代入式(1)右边部分，式(5)代入式(1)左边部分，两边对比，取x前面的系数，可以得到：

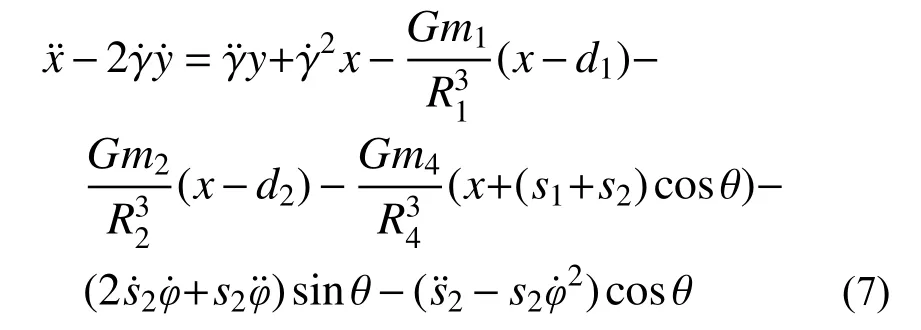
为了分析问题和计算上的方便，在求动力学方程时，往往采用无量纲形式，本文中将各物理量相应的长度单位[L]、质量单位[M]和时间单位[T]分别取为：

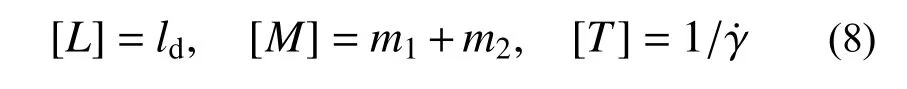
由此，在无量纲系统中，主小行星相对于惯性系的旋转角速度为1，且 P1、P2和P4的质量有：

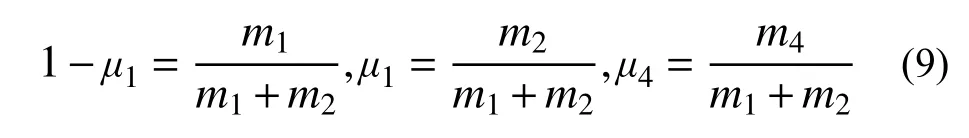
通过主小行星质心和双小行星系统质心可知，在无量纲系统中：

并得到：

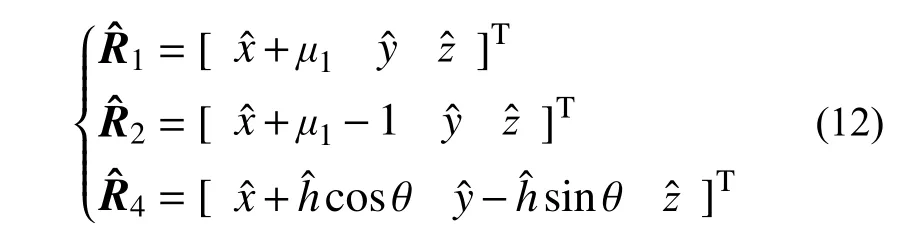
式中，上标“^”表示对应的无量纲量。用ν表示在无量纲系统中双小行星系统相对惯性系的旋转角速度，则：

式中，k为“受力比”，其反映了小行星的自身特性，具有如下的形式：

式中，G是引力常数。

由此，对式(7)进行无量纲化，得到：

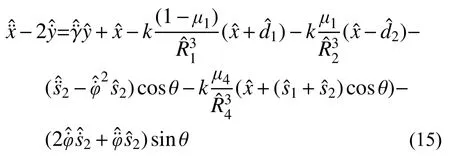
同理，可以得到另外两个方向的方程。此外，由双小行星系统和主小行星均为匀速自转可知：

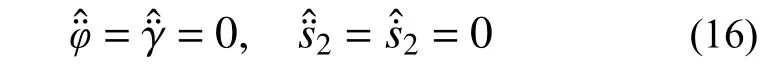
代入后得到探测器P3的动力学方程。为方便后续研究工作，用不带“^”的符号表示无量纲物理量，则各分量形式如下：

式中：θ=(1−v)×t+θ0，t为无量纲意义下的时间，θ0为主小行星的初始相位，即在初始时刻，正向Xr轴与正向x轴之间的夹角。

式(17)即为本文关注的双小行星系统普适性引力场模型。根据v的定义，当v=1时，式(17)表示同步双小行星系统的动力学方程；当0＜v＜1时，式(17)表示非同步双小行星系统的动力学方程。

2 同步双小行星系统平衡点及其稳定性

当双小行星系统同步运转时，即双小行星系统旋转的角速度和主小行星自转角速度一致时，ν=1。此时动力学方程为：

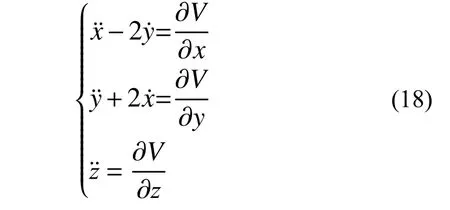
式中，V为有效引力势，其表达式如下：

通过式(18)可以得到一个能量积分：

式中，C为雅克比常数，决定了探测器被允许的运动区域。

应该注意的是，虽然式(18)是建立在B-xyz坐标系下的动力学方程，但是对于同步双小行星系统，由式(18)计算得到的平衡点仍然是整个系统的平衡点。此外，由上述分析可知受力比k、初始相位θ0、质量参数µ1和µ4对平衡点的分布及稳定性都有着重要影响。本章将研究系统参数对于同步双小行星系统平衡点分布及稳定性的影响。

2.1 平衡点分布特性研究

对于同步双小行星系统，给定系统的初始相位后，系统的平衡点是固定不变的。由于偶极子—粒子模型关于B-xy对称，所以系统平衡点都位于该平面内，非共线平动解满足：

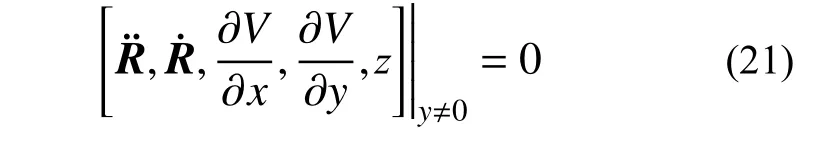
而共线平衡点则满足：

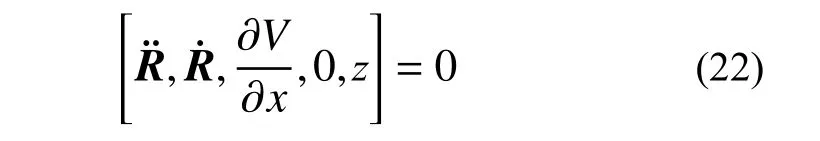
进而通过牛顿迭代法可以得到平衡点的精确位置。

图2是系统参数[µ1，µ4，k]T=[0.7，0.05，9]T且初始相位为0时，系统零速度面等高线以及平衡点的相对位置情况(未考虑小行星内部的平衡点)，其中横轴和纵轴是无量纲意义下的x轴和y轴。该参数条件下平衡点的具体坐标列在表1中。在本文中，坐标系统中的x和 y都代表无量纲坐标。

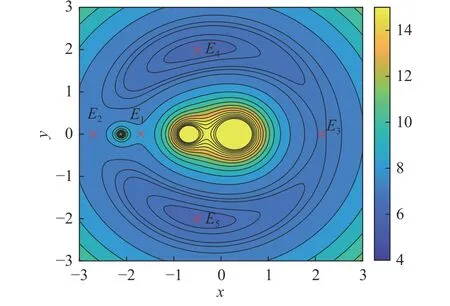
图2 µ1=0.7，µ4=0.05，k = 9时的平衡点以及零速度面Fig. 2 Equilibrium points and zero-velocity curves whenµ1=0.7, µ4=0.05 and k = 9

表1 图2中平衡点位置Table1 The positions of the equilibrium points in Figure 2

表2进一步给出了平衡点位置随系统参数[µ1，µ4，k]T变化时的移动规律。表中：斜箭头符号“↗”表示参数增大；符号“≡”表示参数值固定不变；4个水平方向箭头表示平衡点坐标的移动方向。例如，当受力比k和µ1固定不变时，共线平衡点E2随着µ4的增加向左移动远离主小行星，E1向右移动靠近主小行星，E3向左移动靠近主小行星。非共线平衡点E4的x分量向左移动，y分量向上移动远离双小行星系统，E5与E4始终保持对称。当µ1和µ4固定不变时，共线平衡点E1和E2随着受力比k的增加向左移动，而共线平衡点E3向右移动，非共线平衡点E4的y分量向上移动，总之，平衡点随着受力比k的增加而全部远离双小行星系统质心。当k和µ4固定不变时，所有平衡点随着µ1的增加变化趋势都会出现转折，比如，共线平衡点E3随着µ1的增加先向右移动再向左移动，即共线平衡点E3先远离系统质心再靠近系统质心。

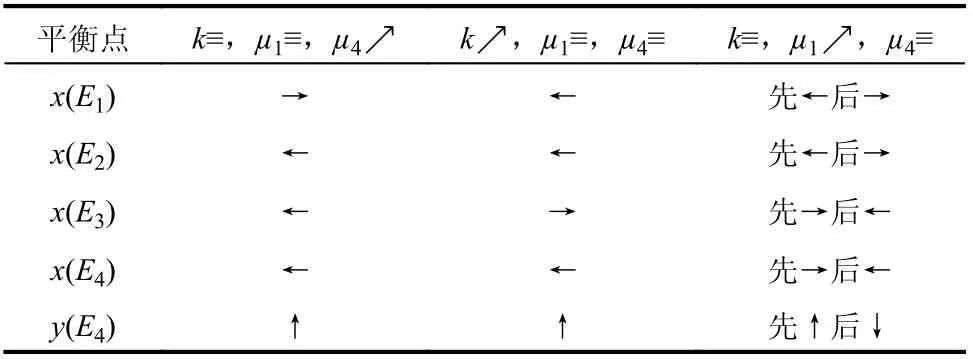
表2 系统平衡点随系统参数变化的移动规律Table2 Variation trends of coordinates for the equilibriumpoints with the change of system parameters

图3给出µ4=0.04时，不同µ1下，非共线平衡点E4位置随k值从9.025减小到0.125的变化情况。由图3可知，对于不同的µ1，平衡点的变化趋势都是随着k减小，x坐标逐渐增加，y坐标逐渐减小，而且µ1值越小，x变化量越大。由于双小行星系统中主次小行星之间的距离应该大于主星质心到两个偶极子之间的距离，否则小行星之间会产生碰撞。图中“×”表示不符合文中模型假设的平衡点，即使得h＜µ1或h＜1−µ1的平衡点。

图3 µ4=0.04，不同µ1下，非共线平衡点E4随k从9.025减小到0.125的位置变化情况Fig. 3 When µ4=0.04, different locations of E4 with variations of µ1 and k

图4中红点表示k=0.1时不同µ1下，非共线平衡点E4随着µ4从0.5减小到0 的位置变化情况。由图4可知，对于不同的µ1，平衡点的变化趋势都是随着µ4减小，x坐标逐渐增加，y坐标逐渐减小，而且µ1值越小，x变化量越大。当µ1≤0.5且µ4≠0时，由于系统中次星的存在时，不同于单偶极子模型描述的系统[67]，双小行星系统的非共线平衡点E4并没有消失，依然存在。而当µ4=0时，由于系统退化为单偶极子模型，系统的拓扑构型发生变化，无论µ1如何取值，非共线平衡点E4(或E5)均会消失，而产生新的共线平衡点。为了讨论一般性，两个极限情况k→0和k→∞没有在本文进行探究。此外，当µ1＞0.5且µ4≠0时，计算所得的平衡点均不符合文中模型的描述，即h＜µ1或h＜1−µ1，用“×”表示。

图4 k=0.1，不同µ1下，非共线平衡点E4随µ4从0.5减小到0的位置变化情况Fig. 4 When k=0.1, different locations of E4 with variations of µ1 and µ4

2.2 平衡点稳定性

同步双小行星系统式(18)线性部分的特征方程为：

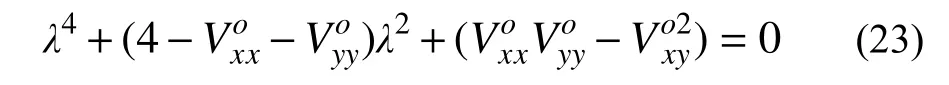
特征方程(23)的根决定了平衡点周围的运动特性。如果特征根具有纯虚根或具有负实部的复根，则平衡点是稳定的。具体的判断条件如下：

基于以上稳定条件，通过牛顿迭代计算发现，共线平衡点是不稳定的，而非共线平衡点存在满足线性稳定性的参数域。由于多数双小行星系统中，次小行星的质量比主小行星的质量小很多，即µ4较小。因此仿真中，µ4取值为0.005～0.040，µ1取值为0～1，k则取值1～100，稳定边界曲线结果如图5(a)所示。当系统参数取值位于该曲面上方区域时，系统具有稳定的非共线平衡点；反之则存在不稳定的非共线平衡点。图5(b)和图5(c)分别为图5(a)在µ1-k平面和µ4-k平面的投影。

从图5(b)中可以看到，当µ4比较大时，稳定边界曲线峰值较高，对应k值较大，且曲线向右偏斜；而当µ4较小时，稳定边界曲线峰值下降，稳定域变大，对应k值较小。当µ4=0.005时，其曲线基本关于µ1=0.5对称，非常接近单偶极子模型的稳定域情况[67]。由此可知，次小行星质量越小，系统平衡点的稳定边界所对应的k值越小。对于特例µ1=0或者µ1=1(两者所对应的系统一致)，此时双小行星系统的主小行星已经简化为一球体，系统退化为限制性三体问题系统，稳定域内k的最小值为1，与限制性三体问题结论一致。

当µ1固定不变时，非共线平衡点E4稳定性随参数k和µ4变化规律如图5(c)所示。各曲线下方为不稳定区域，上方为稳定区域。由图5(c)可知，当µ1的值保持不变并不断增大µ4时，受力比k的临界值会不断增大。特别的，当µ1≤0.2或µ1=1时，k的临界值几乎为一常值，使得平衡点的不稳定区域近似为一个矩形。这表明，同步双小行星系统在µ1≤0.2或µ1=1后，次星对系统非共线平衡点稳定性的影响已非常小，几乎可以忽略不记。

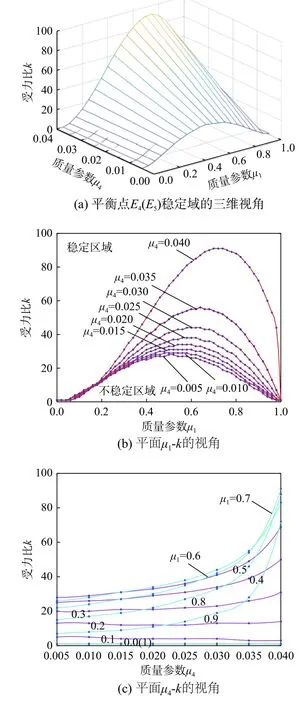
图5 非共线平衡点的线性稳定域Fig. 5 Linear stable area for non-collinear equilibrium points

另外发现随着µ4逐渐增大，平衡点稳定性的规律会发生变化。当µ4=0.05时，非共线平衡点不再具有以上规律，只是µ1和k在很小的时候平衡点具有稳定性，如图6所示。图中阴影区域是非共线平衡点的稳定域。

图6 µ4=0.05时非共线平衡点的线性稳定域Fig. 6 Linear stable area for non-collinear equilibrium points when µ4=0.05

综上所述，偶极子—粒子模型在系统质量固定且次星质量µ4较小的情况下，受力比k越大，非共线平衡点越稳定。即，主小行星系统质量固定且杆长度不变的情况下，主小行星自转角速度越小，平衡点越趋于稳定。

2.3 初始相位对平衡点的影响

由式可知，有效势能V与初始相位θ0相关。不同的初始相位会造成系统的对称性发生变化，使得系统平衡点的个数及位置出现变化。

在 本 小 节 以 系 统 参 数 [µ1，µ4，k]T=[0.7，0.05，9]T为例来说明初始相位对平衡点的影响。对于不同的初始相位，系统平衡点的个数和位置可以通过零速度曲线进行判断，然后再用牛顿迭代法计算出平衡点的精确值，见附录A。由于系统关于原点对称，所以文中考虑0°～180°相位变化如图7(a)～图7(f)所示。

从图7(a)～图7(f)可知，随着初始相位变化，所有平衡点的位置均发生变化。在初始相位从0°～90°变化过程中，次小行星的位置发生变化，它会“挤压”非共线平衡点E4，同时会“吸引”另一个非共线平衡点E5。而当次小行星到达初始相位为0°时平衡点E4的周围时，在“吸引”过程中将“拉扯”出2个新的平衡点E6和E7，平衡点的个数由5变为7。在初始相位从90°～180°变化过程中，次小行星会将继续“挤压”平衡点E4，最终使得平衡点E3和E4“湮灭”，平衡点的个数减少为5。

图7 平衡点和初始相位从 0°～180°变化双小行星系统在x-y平面的零速度曲线Fig. 7 Equilibrium points and the zero-velocity curves in the equatorial plane when the initial phase changes from 0°～180°

图7给出了平衡点随着相位θ0的变化变化情况，此时θ0表示二元系统的相对构型。而自然系4 2 0统在能量上倾向于绕其最大惯性轴旋转，这一构型有能量稳定的解[68−69]，所以图7(a)和图7(g)(初始相位为0°或180°)代表的双小行星系统是稳定的。

3 非同步双小行星系统的等效平衡点运动轨迹

当0＜v＜1时，式(17)表示非同步双小行星系统的动力学方程。令方程右侧等于0能够得到非同步情况下的等效平衡点。假设系统参数 [µ1，µ4，k，v]T=[0.7，0.05，9，0.1]T，并设θ0=0。初始时刻t=0时，各等效平衡点位置情况如图8所示。值得注意的是，为了更清楚地表示等高线和平衡点位置的关系，次小行星外侧存在一等效平衡点E5并未在图中表示。

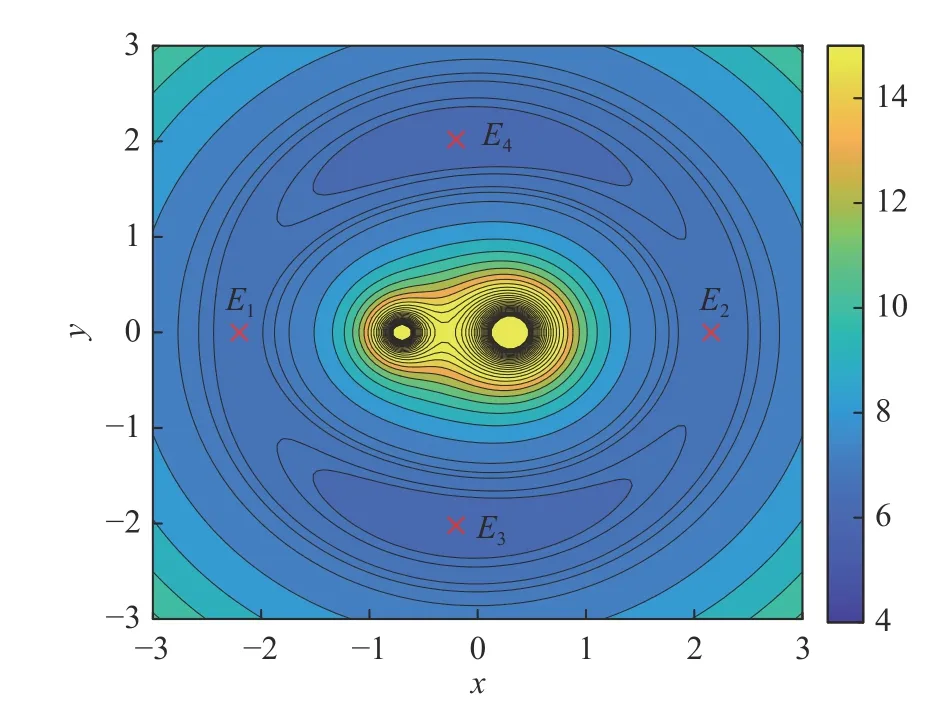
图8 初始时刻非同步双小行星系统的零速度曲线Fig. 8 Equilibrium points in the non-synchronous state and the zero-velocity curves at the initial moment

在一个θ的周期内，图9、图10、图11～图13分别展示了这5个等效平衡点在x-y平面的轨迹，其中黑点表示在初始时刻等效平衡点的位置。可以看出，在该模型的假设下，非同步双小行星系统的等效平衡点的轨迹是周期性的。其中等效平衡点E1和E2、等效平衡点E3和E4的轨迹变化规律相似，等效平衡点E1和E2在x方向上的变化小，等效平衡点E3和E4在y方向上的变化小。等效平衡点E5的轨迹呈近圆形轨迹。

图9 等效平衡点E1的轨迹Fig. 9 Trajectory of equivalent equilibrium point E1

图10 等效平衡点E2的轨迹Fig. 10 Trajectory of equivalent equilibrium point E2

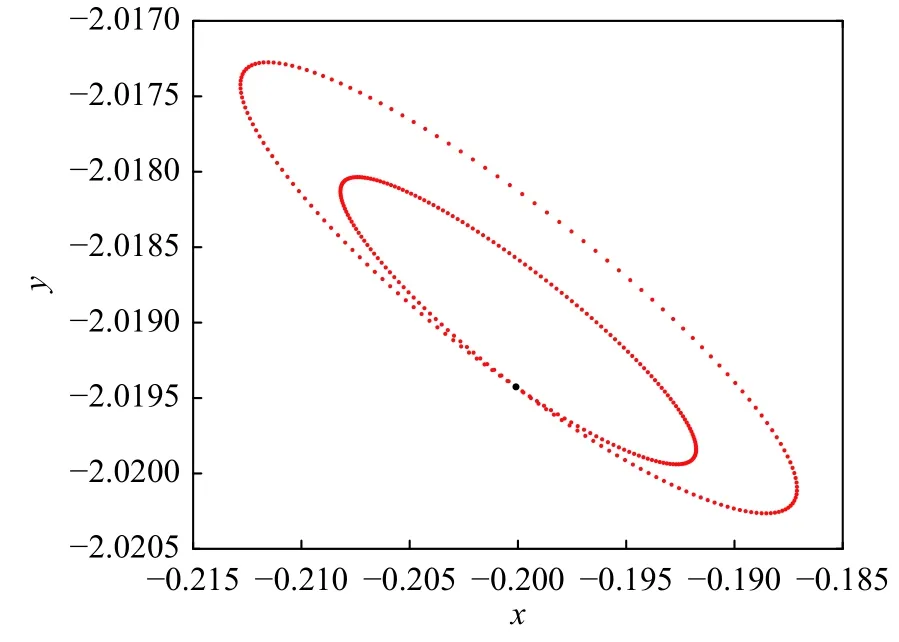
图11 等效平衡点E3的轨迹Fig. 11 Trajectory of equivalent equilibrium point E3

图13 等效平衡点E5的轨迹Fig. 13 Trajectory of equivalent equilibrium point E5

4 同步双小行星系统共线平衡点附近的轨道族

同步双小行星系统的共线平衡点具有特殊的空间位置和动力学特征。利用共线平衡点在旋转坐标系中位置固定的特性，可以实现双小行星系统的观测任务。例如，在围绕平衡点E1的Lyapunov轨道上，探测器能够同时实现观测两个小行星的任务。然而，文中偶极子—粒子模型不同于限制性三体模型，无法采用解析法求解系统的三阶解析解。因此本节将基于平动点周期轨道垂直穿越庞加莱截面的几何对称性，利用路径搜索修正法探索周期轨道[70−71]。再使用伪弧长延拓法寻找同步双小行星系统共线平衡点附近的周期轨道族。

图12 等效平衡点E4的轨迹Fig. 12 Trajectory of equivalent equilibrium point E4

4.1 同步双小行星系统的周期轨道

在x轴上取一点[x0, 0]，作为平动点周期轨道搜索起点，轨道的初值速度设置为[0,]。雅可比常量前文已给出，那么对于初始速度，有：

式中，V是起点[x0, 0]处的有效势能。

通过改变C的大小，能够得到一系列起点在[x0, 0]的轨道。记录穿越x轴时的速度和对应的雅可比常数[C]。在-C曲线中，0对应的初始状态是周期轨道初值的理想猜测值。

假定系统参数为[µ1, µ4, k]T=[0.7, 0.05, 9]T，初始相位为180°。本节将利用上述方法来搜索E1、E2和E3附近的周期轨道。在共线平衡点E1附近，设置搜索起点x0=1.5。图14是雅克比常数C与轨道首次穿越x轴时速度分量的关系。从图中可以看出，曲线与=0交于A、B两点，运用单步打靶法可求得A和B处的轨道精确初始状态为[1.500 954 738 784 62;0;0;0; 1.981 369 681 868 90;0]T和[1.500 496 445 354 81;0;0;0;1.683 561 820 199 68;0]T，对应周期分别是3.700 567 127 127 2和3.856 824 801 326 6。

图14 起点为x0=1.5时雅克比常数C与速度的关系曲线Fig. 14 The relationship between Jacobian constant C and velocity component when x0=1.5

采用图14中A、B处的初值，通过积分可得到图15中的轨道。图中实线代表B处轨道，虚线代表A处轨道。其中，轨道A是围绕次小行星的逆行周期轨道，而轨道B是围绕共线平衡点E1的Lyapunov轨道。

图15 A、B处的周期轨道Fig. 15 The periodic orbits in A and B

类似的，在共线平衡点E2附近，利用上述方法可得到雅克比常数C与从x0=2.5出发的轨道首次穿越x轴时速度分量的关系曲线，如图16所示。图中，D、E处均可能存在Lyapunov轨道。利用单步打靶法可求得精确初始状态分别为[2.500 303 091 710 3;0;0;0;0.904 595 587 122 23;0]T和[2.502 000 755 613 91;0;0;0;0.692 197 762 539 07;0]T，且相应周期分别是3.750 056 994 207 15和2.488 268 157 419 96。

图16 起点为x0=2.5时雅克比常数C与速度的关系曲线Fig. 16 The relationship between Jacobian constant C and velocity component when x0=2.5

采用图16中D、E处的初值，通过积分可得到图17中的轨道。图中，实线代表D处轨道，虚线代表E处轨道。其中，轨道D是围绕平衡点E2的平面Lyapunov轨道，轨道E则是围绕次小行星P4的顺行轨道。

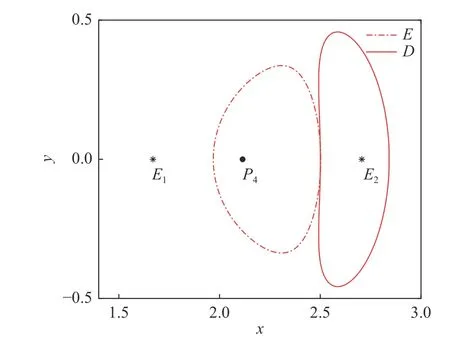
图17 D、E处的周期轨道Fig. 17 The periodic orbits in D and E

在共线平衡点E3附近，利用上述方法可得到雅克比常数C与从x0=−2.5出发的轨道首次穿越x轴时速度分量的关系曲线，如图18所示。图中，F、G处均可能存在Lyapunov轨道。由此，求得周期轨道的精确初始状态分别为[−2.501 175 834 544 529;0;0;0;2.300 538 550 025 692;0]T和[−2.498 584 107 628 348;0;0;0;0.757 759 3649 790 15;0]T，且相应周期分别是2.960 621 259 436 86和5.373 663 202 852 81。

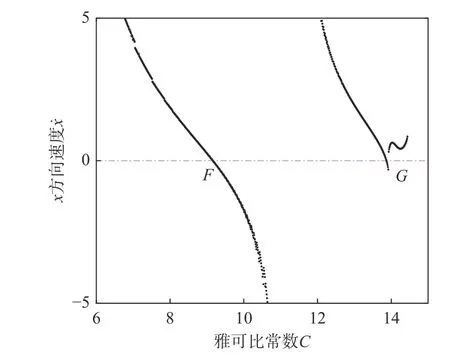
图18 起点为x0=−2.5时雅克比常数C与速度的关系曲线Fig. 18 The relationship between Jacobian constant C and velocity component when x0=−2.5

采用图18中F、G处的初值，通过积分可得到图19中的轨道。图中，实线代表G处轨道，虚线代表F处轨道。其中，轨道G是围绕平衡点E3的平面Lyapunov轨道。值得注意的是，因为轨道F与主小行星会发生碰撞，所以轨道F并不存在。

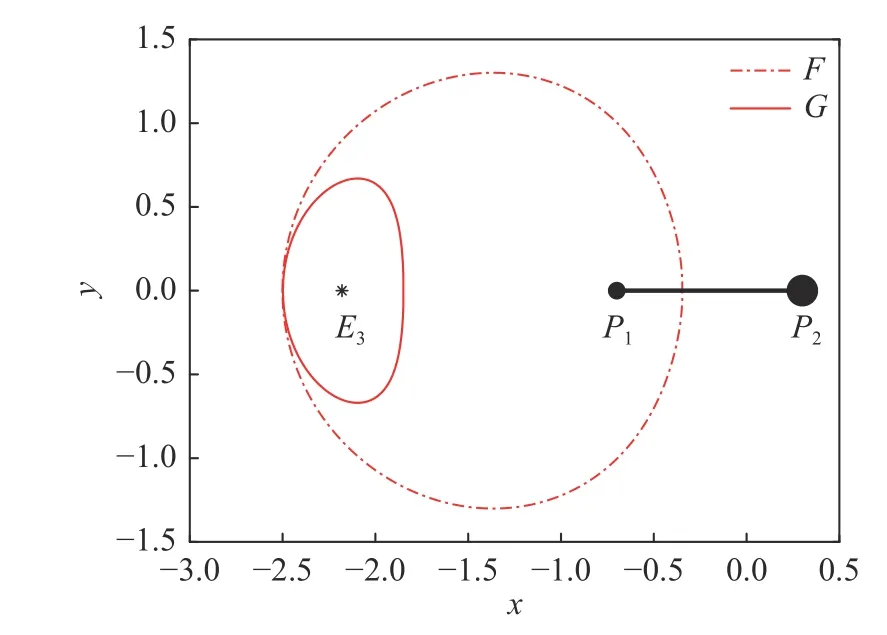
图19 F、G处的周期轨道Fig. 19 The periodic orbits in F and G

4.2 共线平衡点附近的轨道族

通过路径搜索法发现了双小行星系统在平衡点E1、E2和E3周围存在平面周期轨道，再采用伪弧长延拓法则可以找到周期轨道所对应的轨道族[72]。具体步骤如下：

1) 从路径搜索方法中可以得到周期轨道的一个初值猜测，修正得到第一个初值状态。略微改变搜索起始点，能得到与第一个初始状态非常接近的第二个初值状态。

2) 定义状态参数Z。

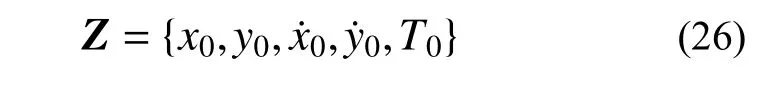
对于平面问题，这5个参数确定了周期轨道的解。根据第1)步可以得到在第(j−2)条轨道和第(j−1)条轨道的准确周期解(j ≥ 3)，并表示为：

由此，选取在第(j−1)条轨道处的演化方向为：

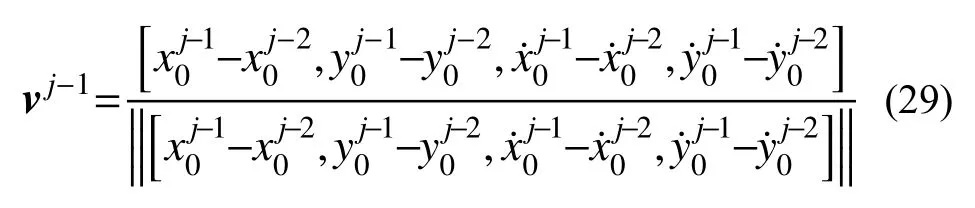
3) 根据在第(j−1)条轨道处的演化方向和准确初值，得到第j条轨道的预测初值：

式中，Δs是很小的预测步长。

4) 通过单步打靶法修正得到第j条轨道准确初值状态。再重复以上步骤。

根据上述数值延拓方法对4.1节中B、D、G处的Lyapunov轨道进行延拓，如图20所示，其中：实线轨道代表围绕E1的轨道，称为轨道族1；虚线轨道代表围绕E2的轨道，称为轨道族2；点划线轨道代表围绕E3的轨道，称为轨道族3。轨道族1、轨道族2和轨道族3的初始状态，周期以及雅克比常数的情况如图21所示。其中x轴、y轴和z轴分别代表轨道初始时刻的位置、速度和雅克比常数，颜色代表轨道的周期。平衡点E1、E2和E3的雅克比常数分别是C1= 15.954 356 339 033 744，C2=15.120 681 652 208 280，C3=14.130 225 232 500 724。

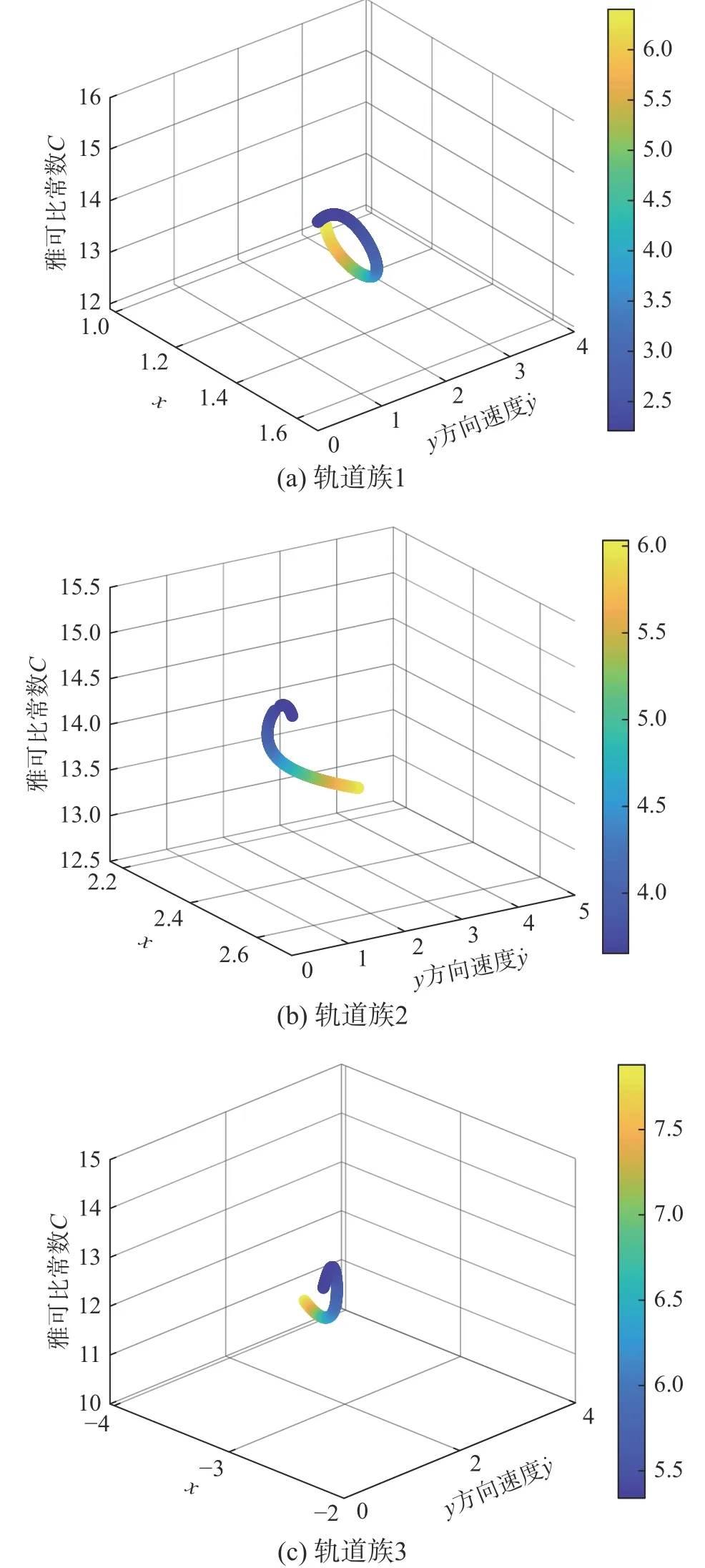
图21 平面Lyapunov轨道族初始位置、周期以及雅克比常数关系图Fig. 21 Initial state, period and Jacobi constant of the planar Lyapunov families

不难发现，这些轨道都是与系统自转角速度φ˙ 、 主星自转角速度接近1∶1共振的轨道族。共振轨道越接近平衡点，轨道周期越小，轨道的雅克比常数越接近平衡点处的雅克比常数。

5 结论

本文采用偶极子—粒子模型研究了主星为细长类小行星的双小行星系统平衡点附近的动力学特性和周期轨道。

文章采用偶极子模型和质量点分别描述细长类主小行星和次小行星，建立了双小行星系统普适性引力场模型。当系统旋转参数v=1时，表示同步双小行星系统；当0＜v＜1时，表示非同步双小行星系统。其次，文章重点讨论了同步双小行星系统的平衡点的分布特征、存在性及稳定性。通过分析可知，在系统质量固定且次星质量µ4较小的情况下，受力比k越大，非共线平衡点越稳定。即，主小行星系统质量固定且杆长度不变的情况下，主小行星自转角速度越小，平衡点越趋于稳定。此外，发现随着初始相位的变化，系统平衡点将随之出现或湮灭。对于非同步情况，给出一个示例并得到了系统等效平衡点的运动轨迹。最后，采用路径搜索法和伪弧长延拓法得到了同步双小行星系统共线平衡点附近的3类1∶1共振轨道族。

本文给出的普适性引力场模型、平衡点的分布和稳定性规律分析结论以及共振轨道族设计方法为双小行星系统探测任务提供了理论基础。