应用结构化思维提高小学数学教学有效性分析

惠高丽 张亦婧

(陕西省西安市经开第二学校 陕西 西安 710021)

结构化思维，与抽象化思维、逆向式思维等相似，都是人类思维方式的一种。在数学学习和生活实践问题的解决中，有时一个新颖、独特的思维方式，往往可以解决很多问题。所谓“思维方式决定了进步和发展的高度”确有其科学的依据在其中。下面本文将首先分析培养小学生数学结构化思维的可行性和必要性，其次，结合小学数学课程谈一谈具体如何培养学生数学结构化思维，以提高小学数学教学的有效性，让学生在数学，乃至宽广的学科领域走的更远。

1.培养小学生数学结构化思维的可行性和必要性

《义务教育数学课程标准(2011年版)》中曾针对学生的“思维”培养提出要求，即“初步学会运用数学的思维方式去观察、分析现实社会，解决日常生活中和其他学科学习中的问题，增强应用数学的意识。”，另外，数学本身就是思维锻炼的体操，它并不像其他文科课程，有很多的背诵内容，更更加侧重于实际的理解、推理、分析和运用，这些过程都与学生的思维、思考方式有着密切的联系。小学生处于人生的学习起点，学习什么知识都会保持好奇、探究的热情，除此之外，如果教师设计的教学内容和教学方法，更加贴合儿童的认知特点和学习规律，那么，他们的探究心理会更强。这显然可以为我们实施小学思维指导，培养学生结构化思维方式提供有利的依据，换言之，即是可行的。

此外，从结构化思维培养的必要性来看，目前小学数学课上和课下辅导中，我们几乎都发现了学生思维片面化、单一化的问题。比如，当教师对学生进行提问后，若全班有一名学生回答正确了问题，那么，其他的学生就是“自然”地停止思考，其间若有持有不同意见或者思路的，也很少再去进行补充，有的数学教师也认为这是“正常”的。还有一种问题，就是学生在解答课后习题时，往往容易在走进思维的误区后，依旧不愿回头，不想尝试其他的思维路径来解答问题，这些都是学生缺乏结构化思维的体现。因此，从有效的解决以上的教学问题，促使学生学会活学活用来看，提高小学生的结构化思维显得尤为必要。

2.培养学生数学结构化思维，提高学科教学有效性的方法

2.1 结合生活，实施结构化思维的启发。数学知识与生活中的很多现象有关，且生活中的很多问题也都需要由数学知识、数学思维来化解。结构化思维，本身就是源自对生活中的人力资源管理问题而总结出来的，所以，学好结构化思维是提高学生社会生活适应能力的关键。在具体实施小学数学教学中，数学教师可以尝试将相关的数学知识整合在一起，并以生活中的某些情境、某些问题为导入线索，结合趣味性的问题和游戏活动，来帮助学生建立对数学概念或者数学思维的理解，形成系统、整体的思维体系，提高学科教学的有效性。

比如，在教学指导北师大版二年级下册的“二位置与方向”的知识时，我们就可以在黑板上绘制一幅学生家、老师家以及学校多个点相对集中的地图，然后，通过“找一找、说一说”的游戏方式，让学生从几个教师提前设计好的“问题纸团”中随机选择游戏任务，被选的“问题纸团”中有：a请找一找小亮家，并根据地图标记的方向和比例尺信息，说出小亮家距离学校有多远，以及相对的位置信息；b请找一找老师家在哪里，并说一说老师家在小亮家的什么方位，相对距离有多远？c如果你现在处于小亮家，找一找地图上哪条行走的线路是最短的，说一说行走的路线和需要行走的总路程。在这样的一个游戏中，就融合了学生一年级学过的“上下、左右”方位知识，以及二年级上册学过的长度单位知识和四则混合运算的计算知识，学生学会解析这一类的问题之后，也将在大脑中逐渐建立一个结构化的思维，从而知晓如何灵活的运用方位、距离和四则混合运算的知识，提高小学数学教学的整体质量。

2.2 指导学生层层深入，让数学思维富有逻辑和秩序。其实数学学习告诉了我们一个道理，那就是数学问题与答案之间存在必然的联系，这种“联系”就是我们思考的过程，也是解决问题的关键。就像当我们意识到口渴的时候，会思考“为什么会口渴？”，导致这个问题出现的因素有哪些？这样可以分析出诸如是否经历了过量的运动导致的水分消耗过快，又如，是否最近很少有机会喝过水，再如，是否过度靠近了热源，导致的水分散发过快等等，之后再由这些决定的因素联想到弥补和挽救的方法，这就是一整套思维连续运行直至解决问题的过程。

而之所以有的学生在思考数学问题时，得不到有效的答案，其原因很大程度上就在于他们无法在问题和答案之间建立思维推理的联系，再具体一些来说，就是他们不知道解答一个数学题需要几个思维的步骤，以及先思考哪个问题、后思考哪个问题等，当思维陷入混乱，而缺乏逻辑性和有序性时，培养学生的结构化思维也就无从谈起了。所以，小学数学教师要科学指导学生思考，本着层层深入，步步为营的原则，让学生在数学思考中逐渐富有逻辑性和秩序性。

比如，在教学指导一年级的“谁的红果多”知识时，通过教学这部分的内容，引导学生观察教材中的图片，学会结合看多少、数数量的方式来比较数量的多与少，从而可以帮助学生建立“差”(减法)的概念，此外，当遇到“谁和谁的数量相等”的时候，则又可以相继引申出“平均分”的概念，而平均分的概念一旦建立，则又可以相继引申出“分数”的认识，这就是数学概念和理论建立时思维的层层深入的结果，在这些新概念的认识中，还可以继续拓展相应的四则混合运算，如此，学生学习的深度和宽度就将得到进一步的延伸。学生的思维越发有序化和逻辑化，这将促使他们在数学探究中逐渐建立学习的自信，继而再次深化结构化数学思维的意识，也为后续更高层次的数学问题数量关系学习奠定基础。

2.3 设计变式训练，指导学生思维变通。在课堂教学中，我们往往会发现这样的一种问题。教师讲完一个数学重点概念或者例题之后，询问学生“大家听懂了吗？”，有的学生不假思索地回答“听懂了”，还有的学生则默不作声，教师再去追问，“有听不懂的同学可以举手提问，有没有？”，在一阵默不作声中教师继续讲解接下来的重点知识。但当稍微设计到刚刚学过的重点内容时，学生又无法理解，或是解题解错，教师反过头来还会责备学生“那我刚刚问你们有没有听懂，为什么不说话呢？”，其实，在笔者看来，他们自己是否真正听懂了即便是他们自己也不知道，或许说他们根本不知晓听懂与没有听懂的区别在哪里，这要让学生自己评价是很困难的一件事。

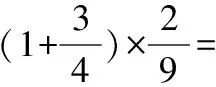
2.4 引导学生自主反思，让学习具备深刻性。众所周知，对事物的认识是存在理性和感性的差别的。而小学生在前期由于对抽象的事物提不起兴趣，故而建立的思维和认识也多偏向于感性的一面。但随着教学的深度提高，以及学生积累的生活经验的丰富，他们也应当试着从感性认识逐渐向理性分析而转变。因为，理性的看待身边的任何问题，往往可以更好的处理和解决实际的问题，这也是在小学时代帮助学生建立结构化思维不可缺乏的过程。

为实现这一教学目标，数学教师要尝试引导学生进行反思、整理和归纳。比如，在教学指导“轴对称图形”的相关知识时，我们就可以启发学生反思以往接触过的图形，如三角形、圆形、正方形、长方形、正五边形、正六边形等等，并用笔将这些图形在稿纸下画出来，然后再来分别找一找这些图形的对称轴在哪里？有几条对称轴？如果仅通过观察很难发现它们的对称轴的话，还可以继续启发学生利用废纸来折一折，剪一剪，在得到每个图形的对称轴及其相应的对称轴数量后，继续对其追问，“是不是随着封闭图形的边数增多，正多边形的对称轴数量也增多了呢？它们之间有什么关系吗？”由此，则可以有效的培养学生的整理、反思和归纳意识，让学生在探索不同的正多边形的性质和特点中，找到它们共有的特征，拓展学生的思维深度，也让本课所教学的内容深深镌刻在学生的大脑中，实现从感性的演示探究，到理性的抽象概括，有效转变学生思维模式，提高教学有效性的目的。

综上，思维的方式可以在很大程度上决定问题解决的效率和结果，生活中有很多的问题，若想达到有效解决的目的，有时需要尝试多种路径，结构化的思维模式，就是让问题得到多元、合理解决的必要因素。数学学科是思维的体操，对于培养学生的结构化思维很有利用的价值和教学的优势。因此，本文从小学数学课的教学角度入手，探讨了几点培养学生结构化思维，提高数学教学有效性的拙见，希望给同仁提供绵薄的参考，以构建更多的有趣、高效数学课堂。