风屏障对流线型箱梁涡振性能影响机理试验研究

李春光，王龙，韩艳，2†，李凯，蔡春声，2

（1.长沙理工大学 土木工程学院，湖南 长沙 410114；2.路易斯安那州立大学土木与环境工程系，路易斯安那巴吞鲁日LA70803）

极端风环境对于桥面行车舒适性及行人的安全性都会造成极其不利的影响.目前风屏障作为改善桥面行车风环境的主要手段已被广泛应用于国内外多座大跨度桥梁，如法国Millau 桥，中国香港青马大桥、杭州湾跨海大桥，英国Severn 悬索桥、Queen Elizabeth 二桥等均加设了风屏障.目前已有学者对风屏障的防风作用做了一定的研究.如李波等[1]采用数值计算的方法，研究了防风栅对高速列车的挡风作用.何玮等[2]采用风洞试验与数值模拟相结合的方法，研究了在桥上设置不同高度的风屏障后车-桥系统的气动参数及桥面周围风环境.黄斌等[3]利用风洞试验的手段，研究了某跨海大桥的桥面风环境，对比验证了加设风屏障后对桥面风环境的优化效果.苏洋等[4]通过足尺模型风洞试验研究了安装风屏障公路桥梁的流场特性及其自身风荷载.周奇等[5]通过数值模拟对不同透风率及不同风攻角下曲线风障的减风效果进行了数值模拟.Gu 等[6]研究了铁路桥上列车不同弯曲角度波纹风障背风面流场的变化规律.He 等[7]通过风洞试验研究了百叶窗型风障对列车和桥梁气动性能的影响.Xue 等[8]通过风洞试验研究了风障参数变化对风-车-桥梁系统气动特性的影响.

以上研究主要针对风屏障对车-桥系统的气动参数或桥面风环境的影响，而关于安装风屏障对主梁气动性能影响的研究相对较少.夏锦林等[9]通过CFD 结合风洞试验研究了不同风屏障形式下桥面风环境及主梁的颤振性能，研究发现主梁安装风屏障后其颤振性能并没有明显恶化.加设椭圆形式的风屏障对桥梁的颤振临界风速有一定程度的提高.但是针对风屏障对桥梁涡振性能影响方面的研究鲜有报道.目前对于钢箱梁截面涡振性能的研究主要集中在抑流板、中央开槽、栏杆位置、风嘴角度等气动措施的影响方面.李春光等[10]通过风洞试验研究了栏杆位置变动对流线型钢箱梁涡振性能影响的机理.胡传新等[11]通过大尺度节段模型测振研究了栏杆扶手抑流板的抑振机理.许福友等[12-13]通过测压法揭示了桥面栏杆抑流板对涡振的控制机理.李春光等[14]通过风洞试验研究了宽幅流线型钢箱梁涡振性能气动优化措施.Nagao 等[15]通过风洞试验研究了栏杆对桥梁涡振的影响.刘志文等[16-17]通过风洞试验研究了钢箱梁涡振性能的影响因素及其涡激力的展向相关性.

本文重点关注风屏障对主梁涡振性能的影响，对某流线型钢箱梁通过风洞测振、测压试验，研究3种不同透风率情况下风屏障对桥梁涡振性能的影响.结果显示，风屏障能有效减弱主梁涡振振幅，消除主梁低风速涡振区间，但是并不能完全抑制涡振的发生.在此情况下提出了安装水平分流板的抑振措施，分析了主梁表面压力分布特性的变化情况，揭示风屏障和水平分流板对该桥涡振性能影响的机理.此外，实际工程中风屏障参数的选取需要综合考虑风障对主梁涡振、颤振性能的影响.

1 工程背景

以国内某主跨为808 m 的大跨径悬索桥为工程背景，该桥主缆矢跨比为1 ∶10，主梁断面采用比较常见的流线型钢箱梁截面，加劲梁宽39.6 m，高3.0 m，宽高比达13.2.桥面一共设置4 道防撞栏杆.主梁底板对称布置两道检修车轨道.主梁标准横断面如图1 所示.

图1 主梁标准横断面（单位：mm）Fig.1 Cross section of main girder（unit：mm）

2 风洞试验概况

2.1 试验布置

主梁节段模型风洞试验在长沙理工大学风工程与风环境研究中心的边界层风洞高速段中进行（如图2 所示），试验段尺寸为21.0 m（长）×4.0 m（宽）×3.0 m（高），风速范围1.0～45.0 m/s 连续可调.试验模型缩尺比为1 ∶50，采用不锈钢方钢管制成主梁节段模型骨架，外衣采用优质木材制作，保证几何外形相似.风屏障高度为3.5 m，透风率分别为30%、45%、60%，风屏障模型如图3 所示.为能够保证主梁断面附近气流的二元特性，在模型两端采用abs 板制作端板来满足上述要求.其余构件与端板加工材料相同.对桥面防撞栏与栏杆，只模拟其外形和透风率.节段模型主要试验参数见表1.

表1 主梁节段模型试验参数Tab.1 Experimental parameters of girder section model

图2 节段模型风洞试验布置图Fig.2 Setup of section model in wind tunnel

图3 不同透风率风障试验模型Fig.3 Wind barrier test model with different air permeability

在节段模型的中央位置布置一道测压点测量模型表面的脉动压力数据，共布置57 个测点.测点布置如图4 所示.通过美国PSI 电子压力扫描阀对各测点的压力时程同步采集，采样频率330 Hz，位移信号通过德国米依激光位移计采集，采样频率500 Hz，采样时间为60 s.

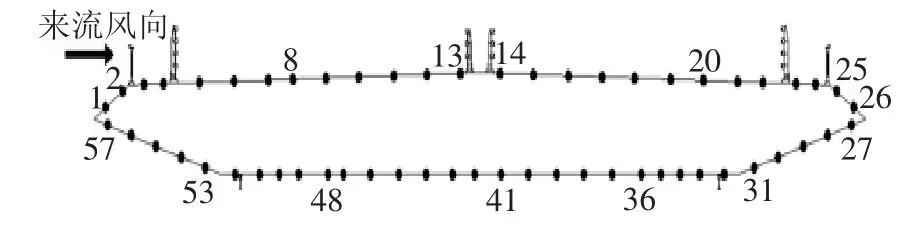
图4 主梁断面测压点布置图Fig.4 Layout of pressure measuring points of main beam section

在风洞均匀流场中进行测振、测压试验，由于+5°攻角下模型竖弯涡振比较强烈，其余攻角均未出现竖弯涡振现象，因此本文研究主要针对+5°攻角展开，共有原断面，30%、45%、60%透风率，加1 m 长水平分流板5 种工况，研究了风屏障对桥梁断面涡振影响的机理，并给出了有效的抑制涡振措施.同时分析了30%透风率时涡振锁定区间（涡振前、上升段、极值点、下降段、涡振后）局部气动力与总体涡激力的相关性以及贡献作用.对应的实桥风速分别为9.54 m/s、10.38 m/s、10.98 m/s、11.77 m/s、12.29 m/s.

2.2 测振试验结果

图5 所示为+5°攻角下5 种工况竖弯涡振位移响应根方差随折减风速U/fB 的变化曲线.横坐标为折减风速U/fB，U 为来流风速，f 为模型振动频率，B为模型宽度.从图5 可看出，原桥在2 个风速区间发生了强烈的涡激共振，涡振振幅分别为0.14 m、0.457 m，竖弯涡振锁定风速区间为U/fB=1.66～2.10、2.93～4.37（风速对应风速区间分别为6.41～8.14 m/s、11.34～16.91 m/s），第二个区间最大振幅约为规范允许值的2.93 倍.安装风屏障之后消除了低风速的涡振区间，最大振幅也有一定程度的减小，且涡振风速区间随着透风率的增加有一定程度向低风速移动的现象.60%透风率时涡振锁定区间变为U/fB=2.10～3.18.

图5 +5°攻角原桥加风屏障主梁竖弯涡振响应曲线Fig.5 Vertical vortex vibration response of the main girder of the original bridge with wind barrier at+5°angle of attack

图6 所示为30%透风率风屏障情况下安装水平分流板时主梁竖弯涡振振幅与风速的变化曲线.由图6 可看出，加了水平分流板具有很好的抑振效果.只有在U/fB=2.10～3.45 风速区间发生了微幅振动，远小于规范允许值.

图6 带风屏障并加装水平分流板主梁竖弯涡振响应Fig.6 Vertical vortex vibration response of main girder with wind barrier and horizontal splitter plate

3 试验结果分析

模型表面的脉动压力数据不仅可以反映断面的气动力分布状况，还可以得到不同工况条件下气动力的演变特性，从而可以揭示风屏障对主梁断面气动性能的影响机理.

3.1 测点压力系数均值

通过模型表面各个测点压力系数均值的空间分布状态可以判断气流在主梁表面的分离与再附.图7和图8 为试验工况最大振幅风速对应的模型表面各测点的压力系数均值.i 测点风压系数的定义：

式中：pi（t）为i 测点风压时程；U0为相应工况下来流平均风速；Cpi（t）为i 测点风压系数时程.

由图7（a）可知，原桥主梁断面上表面的压力系数从2#测点的正值变化到3#测点的负值，主要原因是气流遇到外侧栏杆发生了分离.上表面3#～26#区域内所有测点均处于负压区，说明气流分离后在上表面后部没有出现再附现象.安装风屏障后综合几种工况来看，上表面除风嘴处1#、2#号测点压力系数为正压外，其余测点全为负压，即安装风屏障并未改变来流在主梁上表面的分离与附着，随着透风率的增加，上表面（1#～24#测点）负压有所减小.在风屏障透风率为60%时，6#～23#测点压力系数均值呈现锯齿形状的波动.由图8（a）可知，安装水平分流板后上表面风嘴处正压有所增大，主梁上表面的负压值有所减小.

图7 不同透风率主梁表面压力系数均值对比Fig.7 Comparison of mean surface pressure coefficient of main girder with different air permeability

图8 加分流板主梁表面压力系数均值对比Fig.8 Comparison of mean surface pressure coefficient of main girder with splitter plate

由图7（b）可知，原桥主梁断面气流在模型迎风区斜腹板拐角处发生分离，因此53#测点压力系数由正值突变为负值.由于检修车轨道的存在，会进一步阻碍气流附着主梁表面，因此51#、32#测点出现负压值激增的情况.且随着透风率的增加上游检修轨道附近51#测点压力值呈增大趋势，32#测点与之相反.由图8（b）可知，安装水平分流板后上游斜腹板正压值有所减小，底板中后部负压值有小幅度增加.

3.2 测点压力系数根方差

已有研究表明，主梁表面压力脉动提供大跨度桥梁涡激振动的主要动力.脉动压力根方差能够清楚地反映压力脉动的强弱.

图9 和图10 为试验工况主梁表面压力系数根方差.由图9（a）可知，原桥主梁上表面前部（3#～12#测点）和中后部（15#～23#测点）发生了强烈的压力脉动，可能由于栏杆附属设施的影响在这两个区域产生了强烈的压力脉动，因此可以断定模型上表面前部和中后部附属构件影响产生的强烈脉动压力是激起断面涡激共振的重要因素.对于安装风屏障后模型中后部的压力脉动有一定程度的减弱，因此可以说明涡振的最大振幅有所减小主要是由于模型中后部压力脉动减弱造成的.由图9（b）可知，由于梁底安装检修车轨道的原因，气流流经检修车轨道后产生的气流分离使得各种工况下的压力系数均方差都在32#、51#测点发生了突变，同时安装风屏障使下表面所有测点压力值都有所增加，检修轨道之间区域（32#～51#测点）尤为明显.

图9 不同透风率风屏障主梁表面压力系数根方差对比Fig.9 Root variance comparison of surface pressure coefficient of main girder of wind barrier with different air permeability

由图10 可知，在上下游风嘴处安装水平分流板使得桥梁上表面强烈的压力脉动消失，揭示了水平分流板对主梁涡振具有良好控制效果的作用机理.

图10 安装分流板主梁表面压力系数根方差对比Fig.10 Root variance comparison of surface pressure coefficient of main beam with splitter plate

3.3 测点局部气动力与总体气动力相关性

各测点压力与其代表面积的乘积即为局部气动力，将模型表面所有测压点局部气动力进行矢量积分就可以得到整个测压断面总体气动力.但是通过压力积分获得的总体气动力未包括桥面附属构件上的气动力.通过相关系数可反映局部气动力与总体气动力的相关程度，定义相关系数：

式中：X 为模型某测点处的局部气动力；Y 为各测点局部气动力累加得到的断面总体气动力.R 的取值范围为[-1，1]，相关系数的正负表示两者相关的方向，相关系数绝对值大小表示两者相关程度的强弱.

图11、图12 为安装风屏障以及水平分流板工况上下表面局部气动力与总体气动力相关系数的对比.由图11（a）可知，整个上表面都呈现正相关性，随风屏障透风率的增加上表面除4#、21#测点外所有测点的相关系数都比原断面有所增加，最大值接近于1.由图11（b）可知，对于下表面安装风屏障后（52#～57#、47#～50#）测点的相关性有很大的增强，51#测点由正相关变为了负相关，31#测点的负相关趋势增强，因此，风屏障对检修车轨道之后相近测点的负相关性影响比较明显.37#～46#测点的相关系数有一定的减小，透风率越大减小的程度相对较大.但是由于安装风屏障并没有完全抑制主梁的涡激振动，只是最大振幅有一定的减弱，因此，相关系数的变化并不能反映风屏障对主梁涡振性能的影响.由图12（a）可知，安装水平分流板使得上表面前部以及中后部的局部气动力与总体气动力相关性完全破坏.由图12（b）可知，主梁下表面相关性也有大幅减小.综上所述，主梁上表面前部以及中后部相关性被完全破坏是主梁涡振被抑制的主要原因.

图11 不同透风率风屏障局部气动力与总体气动力相关系数对比Fig.11 Correlation coefficient comparison between local aerodynamic force and overall aerodynamic force of wind barrier with different air permeability

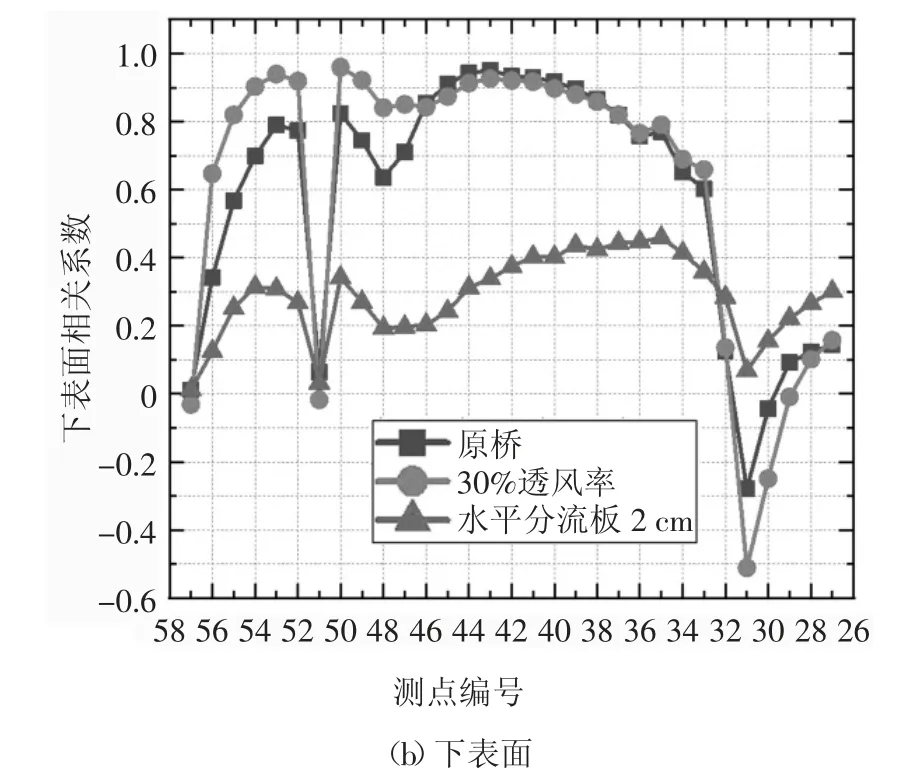
图12 加分流板局部气动力与总体气动力相关系数对比Fig.12 Comparison of correlation coefficient between local aerodynamic force and overall aerodynamic force with splitter plate

图13 所示为30%透风率时涡振锁定区间不同实桥风速9.54 m/s、10.38 m/s、10.98 m/s、11.77 m/s、12.29 m/s 下（涡振前、上升段、极值点、下降段、涡振后）局部气动力与总体涡激力的相关系数.由图13（a）可知，上表面随着涡振振幅的不断增大相关系数不断增大，上表面在靠近中后部均出现上升段相关系数大于极值点处的情况，涡振前和涡振后所有测点的相关系数与涡振锁定区间内相比明显减小.由图13（b）可知，在涡振锁定区间内测点（52#～57#、32#～49#）相关系数出现明显增大，上升段和极值点处在上述两个区间相关性基本一致，下游斜腹板处上升段相关性明显大于极值点处.

图13 涡振过程局部气动力与总体气动力相关系数对比Fig.13 Correlation coefficient comparison between local aerodynamic force and overall aerodynamic force during vortex vibration process

3.4 分布气动力对涡激力的贡献

采用公式（3）计算主梁表面各测点分布气动力对涡激力贡献系数：

式中：ρi为i 测点压力与涡激力的相关系数；Caero-i为主梁表面各测点的分布气动力对涡激力的贡献系数；Cσi为测点压力系数根方差.贡献系数Caero-i的正负只表示测点分布气动力对涡激力的贡献作用为增强或减弱.

图14 和图15 为不同透风率风屏障及水平分流板作用下局部气动力对总体气动力的贡献系数对比.由图14（a）可知，上表面上游靠近栏杆处、上表面中后部贡献系数较其他区域明显增大是产生强烈涡激振动的重要因素（主要是由于该区域内局部气动力与总体气动力相关性的增强并且产生了强烈的压力脉动）.安装风屏障之后上表面中后部区域局部气动力对总体气动力贡献减弱是振幅有一定程度减小的主要原因.同时，在主梁上表面前部（6#～8#测点）45%透风率工况下贡献系数相较于30%、60%两种工况下明显较小，这也可能是此工况下振幅相较于其他透风率更小的原因.由图15（a）（b）可知，原桥和30%透风率工况下主梁上、下表面贡献系数波动很剧烈，尤其是在上表面发生强烈脉动的区域，但是安装水平分流板后上、下表面所有测点对总体气动力的贡献都变得极其微弱，贡献值都趋于0.因此表明分流板在此情况下对涡振有很好的控制效果.

图14 不同风障透风率下局部气动力对总体气动力贡献系数对比Fig.14 Comparison of contribution coefficient of local aerodynamic force to overall aerodynamic force under different wind barrier permeability

图15 加装水平分流板局部气动力对总体气动力贡献系数对比Fig.15 Comparison of contribution coefficient of local aerodynamic force to overall aerodynamic force with horizontal splitter plate

图16 所示为30%风屏障透风率工况下涡振过程局部气动力与总体气动力的贡献系数对比.由图16（a）可知，上升段贡献系数在上表面中后部（11#～24#测点）均比极值点处大.由图16（b）可知，在下表面（52#～57#测点、32#～49#测点）上升段与极值点贡献系数相差不大.

图16 涡振过程测点区域局部气动力对总体气动力贡献系数对比Fig.16 Comparison of contribution coefficients of local aerodynamic force to overall aerodynamic force in measuring point area during vortex vibration process

4 结论

1）依托工程主梁原断面+5°攻角时在6.41～8.14 m/s、11.34～16.91 m/s 两个风速区间均发生竖向涡激振动，后者的涡振振幅达到了0.457 m，远超规范允许幅值（0.155 8 m）.主梁在上表面前部以及中后部产生了比较强烈的压力脉动，且在该区域的相关系数与贡献系数相对较大，可能是诱发主梁强烈涡激振动的重要原因.

2）在桥面安装风屏障之后消除了原桥断面低风速区间的涡振，高风速区间的涡振振幅有一定程度的减小.究其原因是安装风屏障使得主梁上表面中后部压力脉动减弱且贡献系数减小，从而使涡振最大振幅有所降低.

3）在主梁风嘴处加水平分流板完全破坏了主梁上表面前部与中后部局部气动力与总体气动力的相关性，局部气动对总体涡激力的贡献被完全削弱，从而完全抑制了涡激共振的产生.

4）通过对涡振锁定区间（涡振前、上升段、极值点、下降段、涡振后）几个风速代表点进行分析得到在涡振锁定区间内上表面中后部（11#～24#测点）上升段贡献系数相较于极值点明显增大.