高层建筑形状及布局对城市街区行人风环境影响研究

2021-12-01闫渤文魏民鄢乔程勇舒臻孺李秋胜周绪红

湖南大学学报（自然科学版） 2021年11期

闫渤文，魏民，鄢乔，2，程勇，舒臻孺，李秋胜，周绪红，5

（1.重庆大学风工程及风资源利用重庆市重点实验室，重庆 400045；2.湖北省联合发展投资集团，湖北武汉 430061；3.中南大学土木工程学院，湖南长沙 410075；4.香港城市大学建筑学与土木工程学系，香港 999077；5.湖南大学土木工程学院，湖南长沙 410082）

高层建筑物的存在会显著改变城市区域的空气流动，形成包括撞击、绕流、分离及尾流区域等多种复杂的钝体空气动力学现象[1-3].与此同时，随着城市化进程的不断加快，高密度城市区域建筑物间的气动干扰现象愈加突出，导致行人高度处出现显著的高风速区域，进一步加剧了建筑群行人风环境的恶化，影响行人舒适度，更有甚者会危及行人安全，带来行人风环境问题[4].因此，有必要对高层建筑物周边区域的行人风环境进行深入研究，提出改善高密度城市区域行人风环境的方法，进一步落实当前我国发展可持续的绿色宜居城市的战略[5].

国内外学者对建筑物行人风环境做了广泛研究，并逐渐形成了行人风环境的评估流程.主要包含4 方面：当地风气候、周边地形影响、建筑气动特性以及行人风环境评估标准[6].其中，建筑气动特性对行人风环境的影响是当前的研究热点[7].学者们对此展开了广泛的试验研究.Tsang 等[8]对4 个并列布置的矩形高层建筑开展了风洞试验，研究了长宽比、建筑间距对高层建筑周边行人高度处风速的影响.Xu等[9]构建了40 种不同形状的单体高层建筑，研究了建筑形状对行人风环境的作用机理.受到测点数量的限制，风洞试验中无法提供建筑群周围及其全域详细的三维流场.近些年，随着计算流体动力学方法（Computational Fluids Dynamics，CFD）的快速发展以及高性能计算资源的增长，雷诺平均湍流模型（Reynolds-Averaged Navier-Stokes，RANS）、大涡模拟方法（Large-eddy Simulation，LES）以及分离涡模拟（Detached-eddy Simulation，DES）已在城市行人风环境舒适性评估和研究中得到应用.虽然LES 和DES模型能在尾流和分离区获得比RANS 模型更准确的瞬态流场结果，但由于RANS 模型计算效率高，且在高风速区能提供可靠的平均风速模拟结果，仍被广泛应用于行人风环境的研究和工程实践[10-12].Iqbal和Chan[13]结合风洞试验和CFD 数值模拟研究了建筑间距和风向对十字形高层建筑群行人风环境的影响.Van 等[14]结合风洞试验验证了多种RANS 湍流模型，并采用RANS 模型研究了雨棚、露台以及透风楼层等气动外形修正措施对单栋高层建筑行人风环境的影响.但目前行人风环境研究的主要研究对象还只是单栋或者2～3 栋建筑，并且现有研究中建筑物外形多以矩形或者方形为主，缺乏建筑布局以及外形对高层建筑群风环境的影响研究.

基于以上研究现状，本文结合风洞试验和CFD数值模拟，定量分析了等概率全风向下建筑外形及布局对高层建筑群风环境的影响，明确了最优建筑外形和布局，并进一步基于CFD 全域流场结果揭示了建筑外形和布局对高层建筑群行人风环境的影响机理.

1 研究方法

1.1 风洞试验

本次风洞试验在香港城市大学边界层风洞中进行（见图1（a）），试验段尺寸为11.0 m×4.0 m×2.0 m（长×宽×高）.试验来流依据日本规范所规定的Ⅲ类地貌[15]（见图1（b））.试验所采用的模型均由PVC 材料制成，几何缩尺比为1 ∶400；每个高层建筑群模型由8 个相同的单栋高层建筑模型构成，为了保证容积率相同，每一个单体建筑具有相同的高度H（210 mm）和平面投影面积（见图2），模型的阻塞比小于3%.为了研究建筑形状及布局对行人风环境的影响，本文参考了城市街区常见的5 种建筑形状和4种建筑布局，共20 个工况（见表1），风向角间隔30°.结合本文采用的建筑布局和建筑外形，考虑实际试验方案的可行性，在街道、转角以及建筑模型周边布置了26 个测点，测点高度为距地面2.0 m（缩尺后为0.5 cm）的行人高度处（见图3）.风速测量采用kanomax 风速探头，精度为±0.1 m/s，采样频率选用625 Hz.

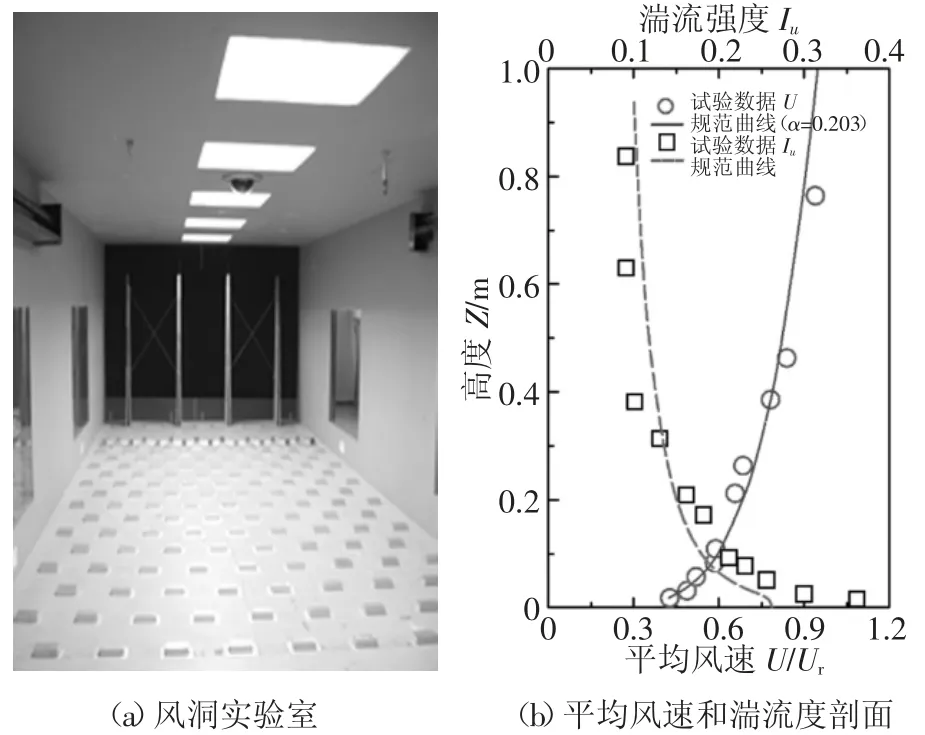
图1 边界层风洞及来流条件Fig.1 Boundary layer wind tunnel and simulated upstream flow conditions

图2 不同建筑外形及布局（5 种建筑形状及4 种布局）（单位：mm）Fig.2 Different building shapes and layouts（five building shapes and four building layouts）（unit：mm）

图3 测点分布图（单位：mm）Fig.3 Positions of wind speed probes（unit：mm）

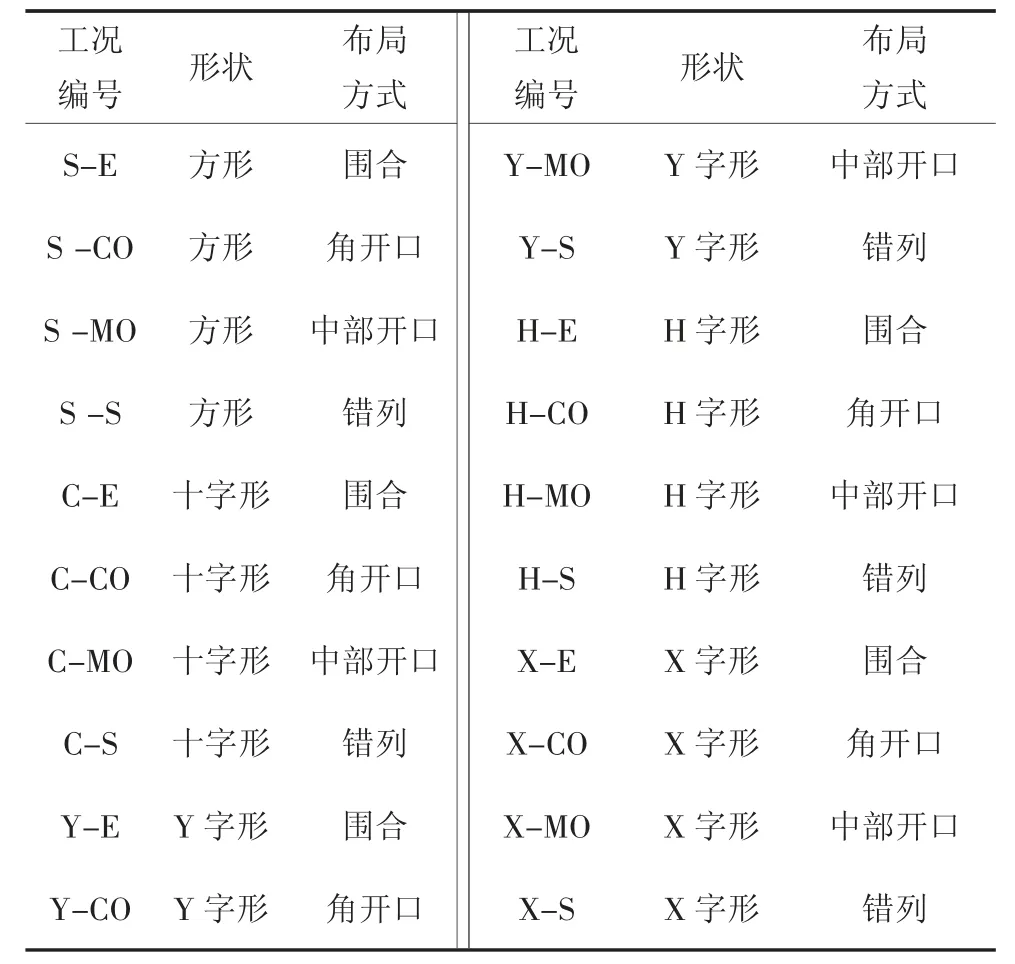
表1 试验工况表Tab.1 Test cases

1.2 CFD 数值模拟

CFD 数值模拟中，所有模型的尺寸均与风洞试验保持一致.计算域尺寸为15H（长）×10H（宽）×6H（高）（如图4 所示），CFD 数值模拟的阻塞率小于3%，满足日本风规范规定的数值模拟计算域大小的要求[15]，无需对结果进行修正[16-17].边界条件设定见表2，入口设置为速度入口（Velocity-inlet），出口设置压力出口（Pressure-outlet），两侧边界及顶部边界均采用对称性边界条件（Symmetry），建筑壁面和地面采用无滑移壁面（No-slip wall）.网格划分采用结构化网格，在建筑物壁面处对网格加密，首层网格高度为0.000 2 m，建筑壁面首层网格y+为30 左右，网格增长率为1.1，所有工况网格总量为7×106～9×106.

表2 边界条件的设定Tab.2 Settings of boundary conditions

图4 计算域及边界条件设定Fig.4 Computational domain and boundary conditions

由于RANS 湍流模型会显著影响数值模拟结果的精度，为了验证不同RANS 湍流模型，本文根据Xu 等人在东京工艺大学（Tokyo Polytechnic University，TPU）边界层风洞中开展的方形单体建筑行人风环境试验结果[9]，分别从定性和定量角度验证了不同RANS 湍流模型的模拟精度，包括标准k-ε 模型、Realizable k-ε 模型、RNG k-ε 模型、标准k-ω 模型以及SST k-ω 模型.其中标准k-ε 模型中的湍流参数依据文献[12]进行了修正，验证湍流模型参数对高风速区模拟准确性的影响.

本文采用基于有限体积法的ANSYS/Fluent 15.0 CFD 数值模拟平台，相应的湍动能、湍流耗散率及平均风速剖面等入口边界条件通过编写自定义函数（User-Define Function，UDF）实现；求解器为基于压力求解的不可压缩流稳态算法，速度-压力耦合方式为SIMPLEC，动量方程和湍流模型输运方程的非线性对流项离散格式为二阶迎风格式（Second order Upwind Scheme，SUS）；模拟收敛准则为所有变量的残差变化稳定，最终观察到k 及ε 残差达到10-6以下，连续方程残差达到10-4以下，且在关键监测点风速值达到平稳.

1.3 来流自保持性

行人风环境CFD 数值模拟研究中，由于行人高度距离地面较近，来流特性易受到地面粗糙度的影响而无法保证风场特性在来流方向上的一致，影响数值模拟结果的准确性.因此，基于RANS 模型的CFD 数值模拟的关键问题之一是验证来流的自保持性，即流体经过地表面时，保证流场沿来流方向的流动特性保持一致[19].本文通过修正壁面函数及粗糙度参数的方法来实现风速的自保持性[20].如图5 所示，在空风场的校验结果中，入口和出口的风速剖面较为一致，具有较好的自保持性.

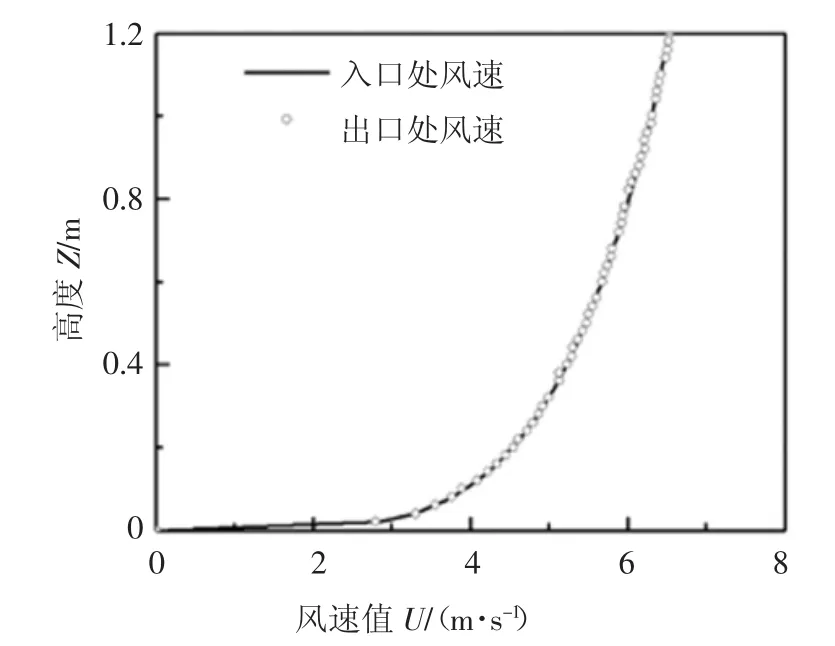
图5 入口和出口风速剖面对比Fig.5 Comparison of predicted profiles of velocity between inlet and outlet

1.4 网格无关性验证

本节以工况S-E-180 为例（网格总数为7×106），建立了两套不同尺寸的网格（稀疏网格首层网格尺寸为0.000 4 m，增长率为1.1，网格总数400 万左右；加密网格首层网格尺寸为0.000 1 m，增长率为1.1，网格总数1 100 万左右）；3 套不同网格对比见图6，同时在图7 中，给出了采用不同网格尺寸得到的26个测点模拟结果.

图6 不同网格划分策略Fig.6 Different grid meshing configurations

图7 结果表明，稀疏网格与基本网格之间的计算结果存在显著差异，而加密网格与基础网格之间的差异却很小.说明采用基础网格进行模拟不仅可以保证计算精度，而且可以尽可能小地消耗计算资源，因此本文所有计算工况网格均按照基础网格方式划分.

图7 网格无关性分析Fig.7 Grid-convergence analysis

1.5 行人风环境评估方法

在对建筑物周边的行人风环境进行评估时，常常采用风速比Ri进行分析[21]，其相关定义如下：

式中：Vi为建筑物周边测点在行人高度处（本文为离地面高度2 m 处）的风速；V0为无建筑物时，入口行人高度处风速.

一方面，从定量的角度，本文通过采用误差度量指标q 进行分析[22]，其定义如下：

式中：N 为测点总数；Riexp、RiCFD分别代表试验结果及其对应的数值模拟结果；q 值最大计算误差为20%.

另一方面，为了定量分析建筑形状和布局对高层建筑群行人风环境的影响，本文采用最大风速比Rmax和归一化加速面积比A*R，avg对建筑群风环境进行量化评估[9]，其相关定义如下：

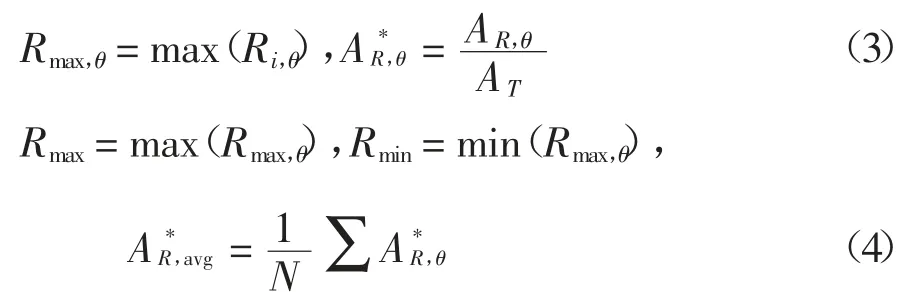
其中AT为评估区域的面积，本文为900×900 mm2，如图8 所示.

图8 加速面积AR，θ 示意图Fig.8 Schematic of speed-up area AR，θ

由前文定义可知，AR，θ中R 值的大小应该为一个大于1.0 的数值.关于R 的具体取值，在缺乏气象统计资料时，要想满足风环境舒适性，主导风向下的风速比不宜大于1.2[23].因此，本文采用Ri=1.2，即计算A1.2，θ的归一化加速面积.

2 结果与讨论

2.1 CFD 结果验证

首先，基于TPU 风洞试验结果，验证了5 种不同的RANS 湍流模型，并将其模拟结果与试验结果进行对比，发现：对于建筑物两侧加速区域的模拟，使用不同的RANS 湍流模型，其模拟结果有所不同，其中RNG k-ε 模型以及修正湍流参数后的标准k-ε模型模拟的效果最好.限于篇幅，此处不再给出相关结果.这与现有研究中RANS 模型对于高风速区域（Ri＞1.0）的模拟较为准确的结论基本一致[10-13].考虑到标准k-ε 模型计算效率更高，本文在后续研究中主要采用经过修正湍流参数的标准k-ε 模型开展数值模拟研究.

表3 为本文开展240 个工况在全部风向角下高风速区（Ri＞1.0）的试验与模拟误差对比结果，并与当前采用RANS 模型开展行人风环境研究的数值模拟验证结果进行了对比.

从表3 可以看出：高风速区，所有测点的最大误差值为20.22%（工况Y-E-150）；最小误差为0.087%（工况H-CO-0）；与现有研究相比（郑朝荣等[24]的最大误差为22.5%，最小误差为1.21%，Iqbal等[13]的最大误差为25.1%，最小误差为1.59%），本文的模拟精度更高，具有较高的可信度.

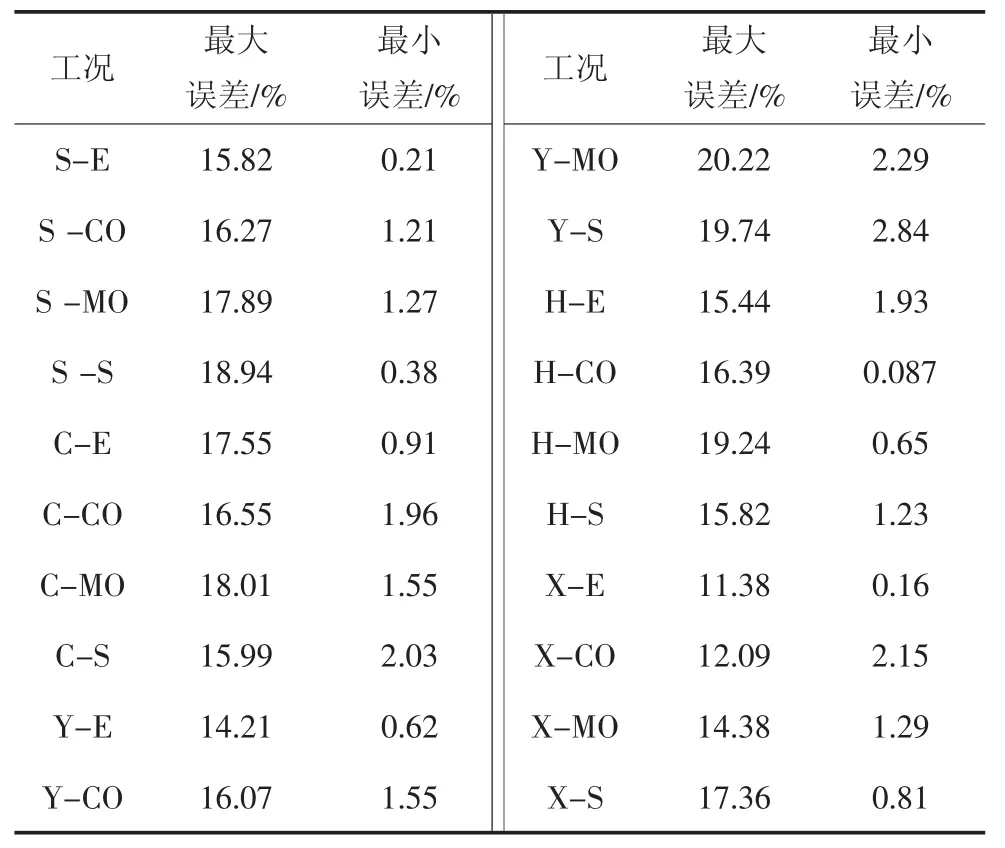
表3 CFD 与试验结果对比Tab.3 Cross-comparison between CFD and test results

为了进一步说明经过修正湍流参数的标准k-ε模型模拟结果的可信度，采用误差度量指标q 进行分析[22]，q 值根据前文计算最大误差选择20%.

图9 统计了所有工况的q 值，发现所有计算工况的q 值均在0.85～0.92 之间，表明本文数值模拟计算的整体最大误差小于15%，数据置信度在0.85 以上.数值模拟在高风速区域可以得到与试验较为一致的结果，但在低风速区RANS 模型结果准确性则较差，主要是因为本文所采用的稳态雷诺平均模型在建筑物尾流漩涡脱落区域（低风速区）低估了尾流中的湍动能，导致数值模拟结果与风洞试验结果相差较大.现有研究表明：采用RANS 模型对行人风环境进行研究时，数值模拟与试验结果在高风速区（Ri＞1.0）高度吻合，其误差控制在0.2 左右，低风速区则准确性较差，与本文模拟结果相同[5].

图9 误差度量指标q 值分布（q=0.2）Fig.9 Distribution of error metric index q

2.2 建筑形状及布局对行人风环境的影响评估

2.2.1 建筑形状对行人风环境影响

为了研究建筑形状对行人风环境的影响，图10、图11 分别给出了不同建筑形状在不同风向角下Rmax，θ和的分布情况.

图10 不同建筑形状的Rmax，θ 分布Fig.10 Rmax，θ of different building shapes

图11 不同建筑形状的的分布Fig.11 of different building shapes

由于错列式分布的Rmax，θ和分布趋势与围合式分布趋势相同，角开口式与中部开口式布局的Rmax，θ和趋势相同，限于篇幅，结果未给出，可参考图10 和图11 分布情况。

从图10 Rmax，θ的分布趋势来看：在围合式布局和角开口式布局下，方形、H 字形及X 字形建筑群的Rmax出现在斜风向下，Rmin则出现在正风向下；而十字形及Y 字形建筑群则与此相反，Rmax出现在正风向下，Rmin则出现于斜风向.对于角部开口式布局，可以得到相同的结论，表明这四种布局不影响不同建筑形状的最有利以及最不利风向角.进一步分析比较，其分布规律与Rmax，θ的分布规律完全相同，即不同布局下，方形、H 字形及X 字形的建筑群的最有利风向为正风向，最不利风向为斜风向；十字形及Y 字形建筑群的最有利风向为斜风向，最不利风向为正风向.

图12 给出了不同建筑形状在围合式布局下，最不利风向角下所对应的行人高度处的风速比云图.通过图12 可以看出：风场中的高风速区域集中在建筑群的侧面及建筑物之间形成的天然廊道中.进一步分析，对于建筑群侧面高风速区域的形成，主要是由于建筑物迎风前缘对风场剪切作用和气流下洗作用联合造成的[24]；而建筑物通道高风速区域，则是由于建筑物之间形成的通风廊道，产生狭管效应现象，使得廊道区域的风速明显增大[25].

图12 最不利风向角下围合式布局行人高度处Ri 云图Fig.12 Contours of Ri of buildings with five shapes in enclosed layout under the most unfavored wind direction

图13 为不同的计算工况在全风向下的最大风速比Rmax与归一化平均加速面积比的分布情况.从Rmax和值的趋势来看，对于这20 种不同的计算工况，Rmax最大值为1.532，最小值为1.468，均位于1.5 附近，相互之间差值仅为4.18%；另一方面比较的大小，明显发现不同工况之间差异很大，最大值为4.02，最小值则为1.67，相互之间的差值超过了140%.因此，在保持高度和容积率一定的情况下，建筑群周边最大风速比不会随着建筑形状和建筑布局的改变而发生明显变化；但建筑形状和建筑布局会改变建筑群周边高风速区域的面积大小，而高风速区域正是本文研究的重点.从Rmax和值的大小来看，围合式布局中，方形围合式布局建筑群的值最小，因此可认为其行人风环境整体上最优；相同的，角开口式及中部开口式布局下，十字形建筑群的整体行人风环境最优；Y 字形建筑群在错列式布局下的行人风环境最优.与之前研究结论基本一致[26-27].

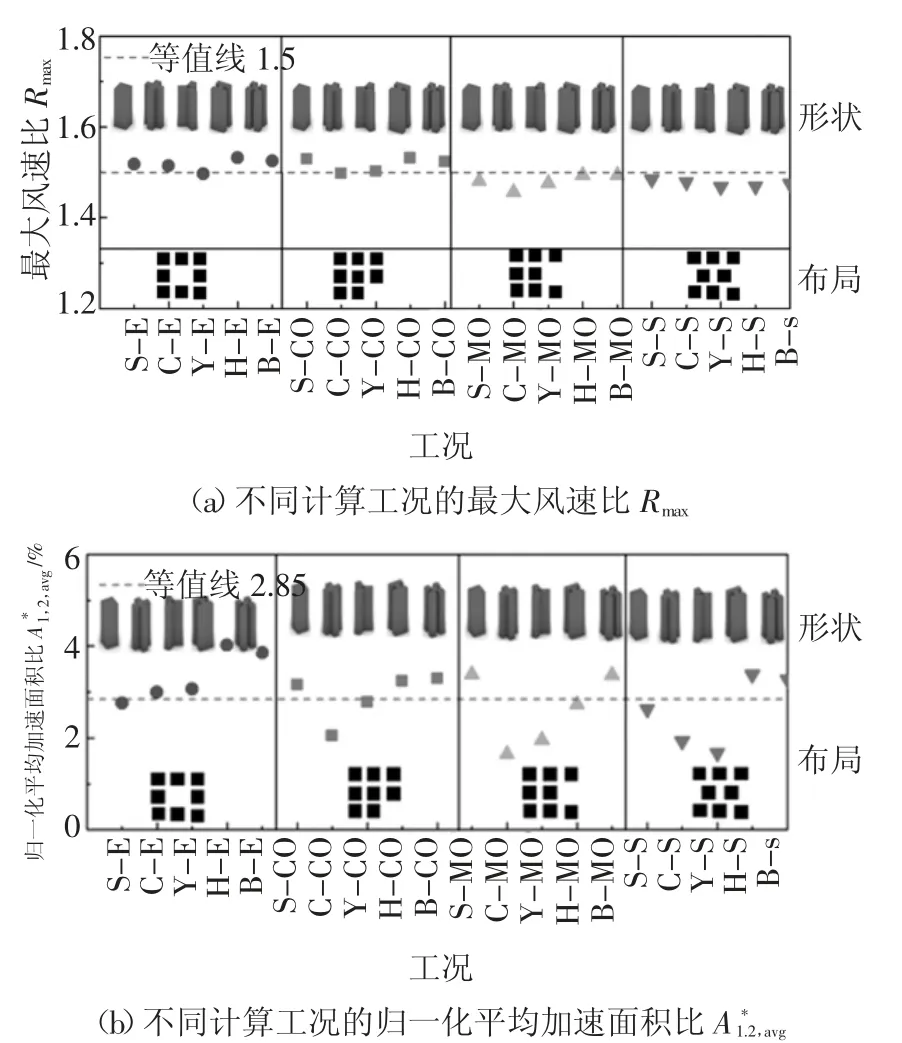
图13 不同计算工况的最大风速比Rmax和归一化平均加速面积比Fig.13 Maximum wind speed ratio and normalized average speed-up area ratio of different test cases

2.2.2 建筑布局对行人风环境影响

由于H 字形及X 字形的Rmax，θ和分布趋势与方形完全相同，Y 字形则和十字形的Rmax，θ和分布趋势相同，因此，本节仅给出了方形和十字形建筑群在不同布局下的Rmax，θ和分布情况.

从分布趋势来看（如图14 和图15 所示），方形建筑群在四种不同布局下，Rmax对应的风向角均为斜方向，而Rmin对应的风向角均与建筑物迎风面垂直；十字形建筑群在四种布局下的结论与方形建筑群相反.这说明在不同布局下，方形、H 字形及X 字形的建筑群的最有利风向角与建筑物侧表面垂直，最不利风向角则为斜风向；而十字形和Y 字形建筑群在不同布局下的结论与前者截然相反.

图14 不同布局下的Rmax，θ 分布Fig.14 Rmax，θ of different building layouts

图15 不同建筑布局下的分布图Fig.15 under different building layouts

图16 和图17 以方形及十字形建筑群为例，分析其作用机理，发现造成建筑群周边区域风速增大的两个主要原因为角部分离效应及狭管效应.由于方形建筑前角的分离剪切作用较大，导致其角部分离效应更加明显，这就使得最不利风向角出现于斜风向下.

图16 最不利风向角下方形建筑群行人高度处Ri 云图Fig.16 Ri contour of the rectangle tall buildings at the pedestrian-level under most unfavorable wind direction

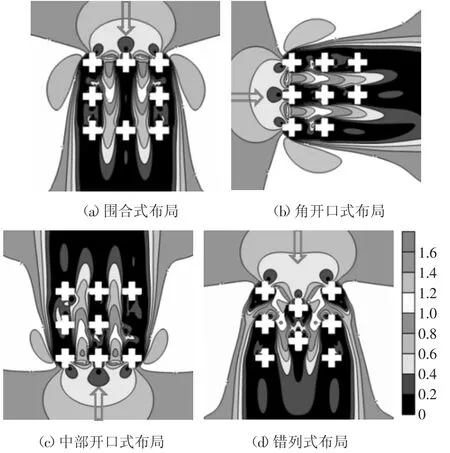
图17 最不利风向角下十字形建筑群行人高度处Ri 云图Fig.17 Ri contour of the cross-shaped tall buildings at the pedestrian-level under most unfavorable wind direction

通过计算不同工况下Rmax和值，从整体上对不同工况的行人风环境进行评估.方形、H 字形及X 字形建筑群均在错列式布局下具有最优的行人风环境效应；十字形及Y 字形建筑群则在中部开口式下具有最优的行人风环境效应.综合考虑建筑布局和建筑形状，风环境最好的是Y 字形错列式布局建筑群，风环境最差的是H 字形围合式布局建筑群.