悬索桥吊索断裂动力响应分析的有限元模拟方法研究

邱文亮，吴广润

（大连理工大学土木工程学院，辽宁大连 116024）

拉、吊索是缆索承重桥（斜拉桥、悬索桥以及中下承式拱桥）中最重要的承重构件，其基本力学性能和耐久性能对结构安全和正常使用产生巨大影响.拉、吊索通常设计有防护措施，具有较高的安全系数，但是桥梁在长期服役期间，拉、吊索出现病害进行维修更换的案例层出不穷，极端荷载作用下桥梁发生断索的报道也屡见不鲜[1].例如，2011 年10 月，印度尼西亚Kutai Kartanegara 悬索桥一根吊索断裂引发吊索连续断裂，最后结构整体倒塌[2].事故发生时工人正在对吊索进行维护保养，造成11 人死亡、30 多人失踪.2019 年10 月，台湾宜兰县南方澳大桥一根吊索断裂，引发结构剧烈振动和相邻吊索连续断裂，最后主梁整体崩塌[3].缆索承重桥拉、吊索突然断裂后剩余结构的内力、变形和刚度将重分配，同时产生显著的动力效应.合理地分析断索事故对桥梁结构服役性能的影响，首先需要对断索动力过程进行准确模拟.

现有规范针对桥梁断索计算仅给出指导性规定，如美国后张法预应力协会（Post-Tensioning Institute，PTI）给出两种断索分析方法：一种是拟动力分析方法，该方法采用静力分析方法加上1 个2.0 的动力放大系数；另一种是动力分析方法.国内已有研究发现，在拟动力分析中桥梁不同构件和截面使用相同动力放大系数不合理，动力分析计算出的结构断索响应更能反映真实情况[4-8].吴庆雄等[9]通过接触碰撞和单元删除的方式进行了拱桥吊杆断裂过程动力分析.曲兆乐等[10]对比了全动力分析方法和半动力分析方法两种模拟斜拉桥拉索断裂失效动力过程方法的特点.悬索桥与斜拉桥、拱桥的结构形式不同，在断索动力分析中主缆振动和吊索冲击作用均起到重要作用，断索造成悬索桥连续倒塌及结构破坏机理也不同.此外，悬索桥断索分析中涉及吊索断裂模拟方式和影响结构动力响应的因素也有待进一步探究.

基于拆除构件法，本文详述了瞬时刚度退化法、瞬时加载法以及等效卸载法，3 种模拟吊索断裂动力过程的基本原理.以某自锚式混凝土悬索桥为工程背景，采用有限元软件ABAQUS 建立了全桥模型，对悬索桥断索动力分析方法和影响因素展开研究.

1 悬索桥断索动力分析方法

拆除构件法又称为变换荷载传递路径法，广泛应用于建筑结构构件失效和连续倒塌分析[11-12].该方法不考虑构件破坏原因，只关注构件失效后剩余结构响应.桥梁断索后结构的初始响应由几何突变后构件振动引起，基于拆除构件法悬索桥断索有限元动力分析可以采用刚度退化法、瞬时加载法和等效卸载法.

1.1 刚度退化法

悬索桥是多自由度体系结构，其基本动力学平衡方程为：

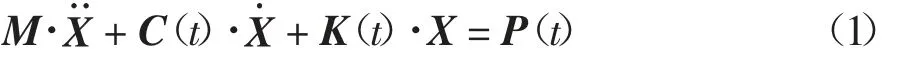
式中：M 为结构质量矩阵；X 为结构位移矩阵；C（t）为结构阻尼矩阵，分析中采用线性瑞利阻尼；K（t）为结构总刚度矩阵，构件失效会导致K（t）改变；P（t）为施加在结构上的荷载矩阵.如图1 所示，破断拉索从开始失去内力到完全失去承载力所经历的时间定义为断索持续时间Δt.

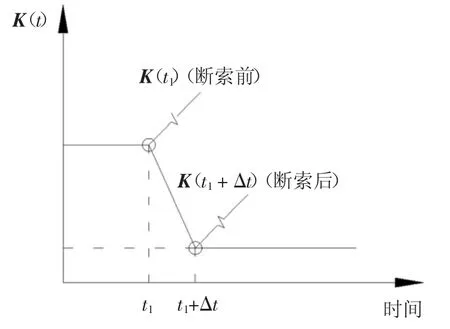
图1 结构整体刚度矩阵随时间变化Fig.1 Change of structural stiffness during the cable rupture process

在有限元分析中，通过瞬时刚度退化法进行吊索断裂模拟有两种方式：一种是移除失效吊索；另一种是改变失效吊索刚度.无论采取哪种方式均能改变结构总刚度矩阵，使断裂吊索的内力转变成惯性力施加于剩余结构上，进而引起结构产生动力响应.

1.2 瞬时加载法和等效卸载法

与刚度退化法模拟吊索断裂过程的机理不同，改变结构动力学平衡方程中荷载矩阵也可以模拟断索动力过程.通过施加动荷载来进行悬索桥断索动力分析有两种方式[6]：一种是断裂吊索依然保留在结构上的突加荷载法，如图2（a）所示；另一种是移除断裂吊索的等效荷载卸载法，如图2（b）所示.

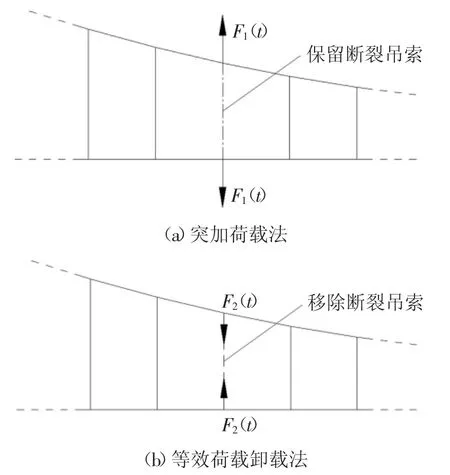
图2 突加荷载法和等效荷载卸载法Fig.2 Demonstration of the instantaneously loading method and unloading equivalent force method

采用突加荷载法模拟吊索断裂，首先在失效吊索两端施加一对随时间变化的拉力，记为F1（t），如图3（a）所示.由于失效吊索仍保留在分析模型中，其拉力会随着F1（t）的增长而增加，直至结构达到平衡状态，此时吊索拉力等于所施加外力.采用等效荷载卸载模式模拟吊索断裂，首先需要移除吊索，同时在移除吊索两端施加一对与拉索内力大小相等方向相反的拉力，记为F2（t），如图3（b）所示.等结构振动稳定后再将F2（t）减小为0.

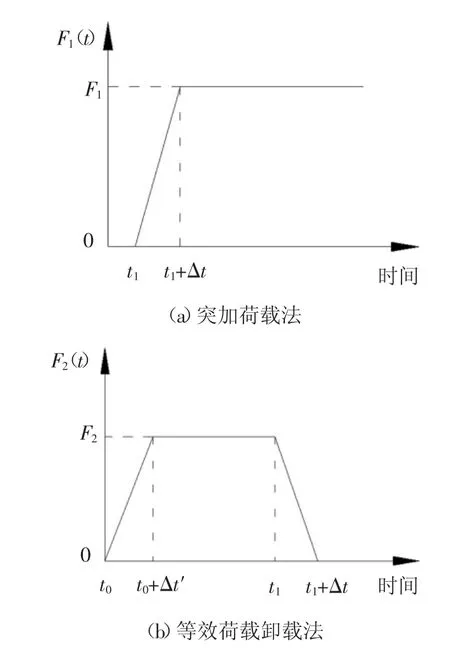
图3 施加荷载时程曲线Fig.3 Time-history curves of the applied load

悬索桥进行断索动力分析时主缆振动的影响不可忽略，而断索前主缆初始状态直接影响断索后主缆振动.瞬时加载法和等效卸载法两种模式有各自的优点和局限性.瞬时加载法在全桥计算模型上保留了失效吊索，可以较真实地反映断索前的状态，但有限元模型中包含了断索后结构中并不存在的单元，并且确定F1需要多次迭代.等效荷载卸载法在断索分析时删除了失效吊索，可以更好地捕获断裂后的结构状态.

1.3 断索动力响应的影响因素

悬索桥吊索断裂引起结构响应的动力效应与Δt密切相关，从结构动力学基本知识可推断，断索后结构最大动力响应会随着Δt 增大而减小.吊索断裂伴随着复杂的机械作用和内力重分配，引起吊索断裂的原因不同（例如锈蚀、火灾、车辆撞击和爆炸），吊索断裂过程中其拉力随时间变化会有极大差异.吊索可能会在很短的时间内发生断裂，吊索承载力会在瞬间丧失，吊索断裂也可能是一个逐渐损失承载力的过程.为了描述断索过程中吊索拉力随时间变化的关系，假定吊索断裂独立于其诱发原因，通过Δt和吊索拉力损失函数lrel（t）描述吊索断裂的不确定性[13].吊索拉力损失函数采用幂指数函数，数学表达式为：

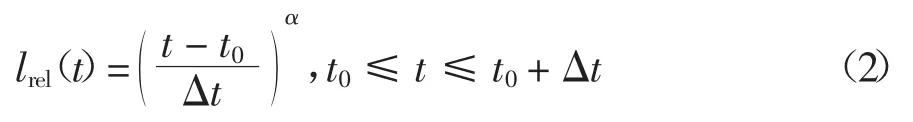
式中：α 为损失函数指数因子.相同Δt 内吊索不同模式的断裂过程可通过改变α 实现，如图4 所示.当α=1 时，吊索内力损失函数为线性关系，内部钢丝在Δt 内均匀地发生断裂.

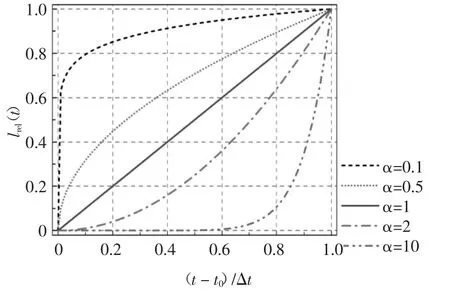
图4 断裂吊索拉力损失函数Fig.4 Tension loss function of the failed hanger

采用上述假定，失效拉索内力变化关系为：

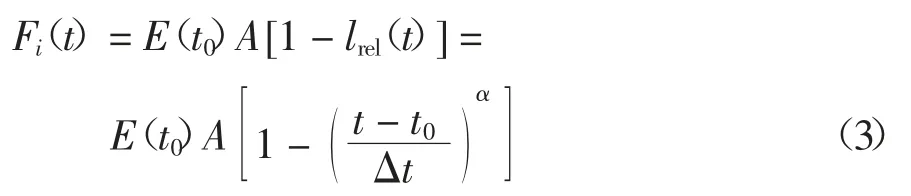
式中：E（t0）为拉索弹性模量；A 为拉索面积.

已有桥梁断索案例表明，断裂吊索的破断位置存在很大的不确定性，统计数据表明[14]：大部分拉、吊索断裂部分集中在锚固区根部，少部分断裂位置集中在索体.采用刚度退化法进行断索分析时设定两种工况：工况1 表示失效吊索单元全部删除；工况2表示只将断裂部位的吊索单元删除.为了考虑同一根吊索断裂位置对断索后动力响应的影响，工况2划分为3 种情形，如图5 所示.

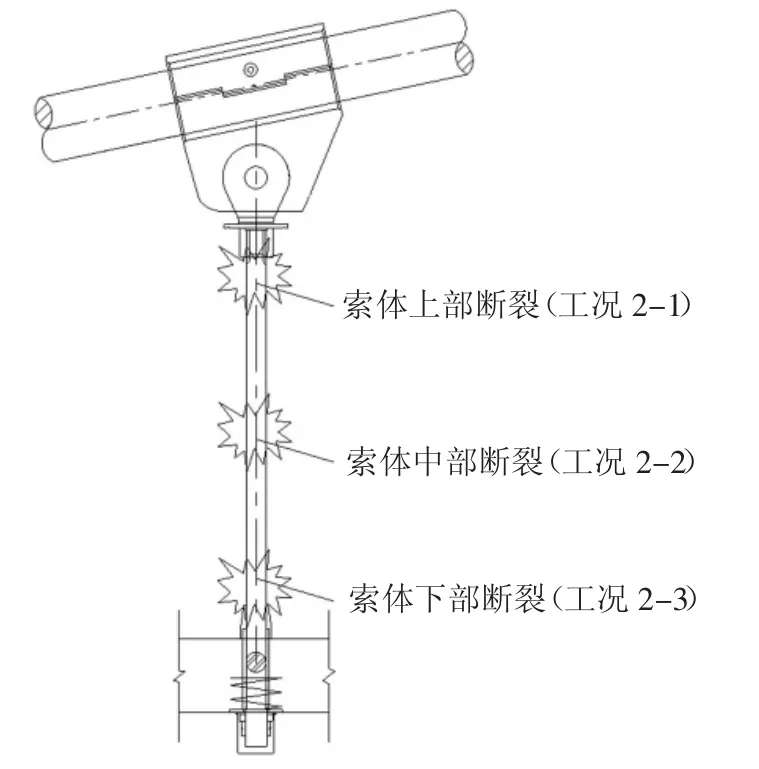
图5 吊索破断位置Fig.5 Failure position of the hanger

2 工程背景及有限元简介

2.1 工程概况

选取某自锚式混凝土悬索桥为工程背景，该桥总宽度为27 m，计算跨径为70 m+200 m+70 m，如图6（a）所示.桥塔为“门”式钢筋混凝土框架结构，索塔高54.5 m，宽30.6 m.主缆对称布置，主跨矢跨比为1 ∶5.5，边跨矢跨比为1 ∶15.7，吊索间距为5 m，全桥共130 根.主缆由32 根169φ5.2 mm 预制平行钢丝索编排而成，吊索由127φ5.2 mm 平行高强镀锌钢丝组成.主梁采用混凝土箱梁，单箱4 室如图6（b）所示.梁高2.5 m，顶板厚0.23 m，底板厚0.22 m，中腹板厚0.35 m，边腹板厚0.45 m.主缆和吊索采用高强镀锌钢丝，极限强度为1 670 MPa，弹性模量为2×105MPa.主梁和桥塔采用C50 混凝土，轴心抗压强度标准值为35 MPa，轴心抗拉强度标准值为3 MPa.

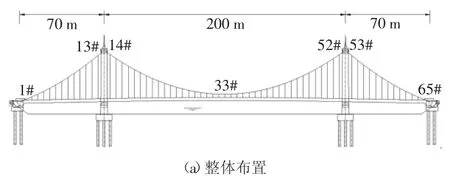
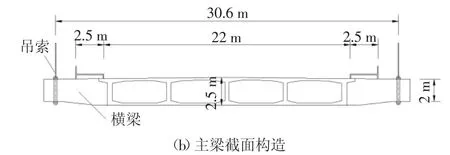
图6 某混凝土自锚式悬索桥Fig.6 Geometry of a typical self-anchored suspension bridge

2.2 有限元模型

全桥有限元空间模型采用ABAQUS2016 建立，如图7 所示.主梁、横梁以及桥塔采用空间梁单元模拟，可考虑扭转质量和扭转刚度.主缆和吊索使用桁架单元模拟，可考虑缆索张力对其弯曲刚度的影响.为了更精确地计算主缆线形和考虑主缆局部振动影响，两个吊索之间主缆划分为4 个单元.吊索夹具使用质量单元建模，质量集中在夹具所在主缆节点上.考虑到索塔的群桩基础对断索分析影响极小，模型中索塔底部采用固结约束.依据梁底布置的支座类型，主梁通过限制自由度来施加边界约束.分析模型基频为0.41 Hz，振型特征是主梁一阶对称竖向弯曲，分析模型一阶扭转频率为1.01 Hz.

图7 全桥有限元空间模型Fig.7 Three-dimensional finite element（FE）model of the bridge

2.3 荷载和断索工况

本研究中悬索桥进行断索动力分析，主要关注断索后结构动力响应，因此仅考虑结构恒荷载.加劲梁、桥塔、主缆和吊索的自重是通过将其横截面积乘以密度自动算出.桥面上二期铺装和附属物的荷载集度为108 kN/m，主缆上保护层的荷载集度为0.37 kN/m.1～9 号、57～65 号吊索夹具重量为12 kN，10～17 号、49～56 号吊索夹具重量为16 kN，18～48 号吊索夹具重量为10 kN.

公路桥涵设计通用规范（JTG D60—2015）规定，悬索桥任何一根吊索的断裂都不应引起结构整体坍塌.近代悬索桥相邻吊索的间距一般不大，在卡车碰撞和爆炸等极限情况下存在多根吊索同时断裂的可能[15-16].本文考虑单根吊索和单边两根相邻吊索同时断裂两种极限情况.为简化分析将桥梁结构划分为5个区域，如图8 所示，各区域分别选取单根吊索和单边相邻两根吊索进行断索动力分析.

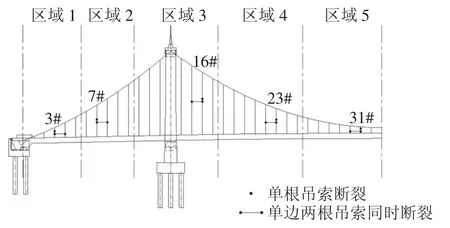
图8 断索工况Fig.8 Hanger-loss scenarios

3 分析结果

3.1 结构的断索时程响应分析

基于刚度退化法，将失效吊索单元完全删除（工况1），图9 给出了7 号吊索断裂后结构动力响应时程曲线.从结果可以看出，Δt 取0.001 s 吊索瞬间断裂后结构响应剧烈波动，Δt 取0.1 s 断索后结构动力响应极值显著下降.如图9（a）所示，7 号吊索瞬间断裂，相邻的6 号吊索应力最大值为826 MPa，达到了其初始值的2.11 倍，Δt 取0.1 s 时6 号吊索应力最大值下降607 MPa.如图9（b）所示，7 号吊索瞬间断裂后主梁弯矩最大值为17.2 MN·m，Δt 取0.1 s 主梁弯矩最大值下降7.6 MN·m.如图9（c）所示，7 号吊索瞬间断裂后主梁扭矩最大值为31.9 MN·m，Δt 取0.1 s 主梁扭矩最大值下降16.5 MN·m.

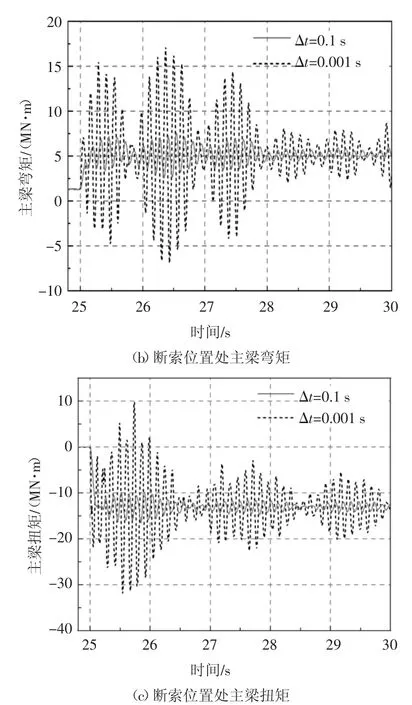
图9 7 号吊索断裂后结构动力响应时程曲线Fig.9 Time-history curves of structural dynamic responses subjected to the breakage of hanger 7

Δt 取0.001 s，采用刚度退化法模拟7 号吊索分别在工况1 和工况2 情况下断裂，表1 给出了结构动力响应极值.结果表明，采用刚度退化法模拟断索时，吊索单元是否全部删除会影响结构断索动力响应，通过删除吊索断裂部位处单元模拟断索时同一吊索断裂位置对动力响应影响不明显.如表1 所示，工况2-1、工况2-2、工况2-3 下结构断索动力响应极值基本相同，工况2 下吊索应力最大值在比工况1下的结果下降了约5%，主梁弯矩最大值增加了约5.8%，主梁扭矩最大值增加了约28.4%.

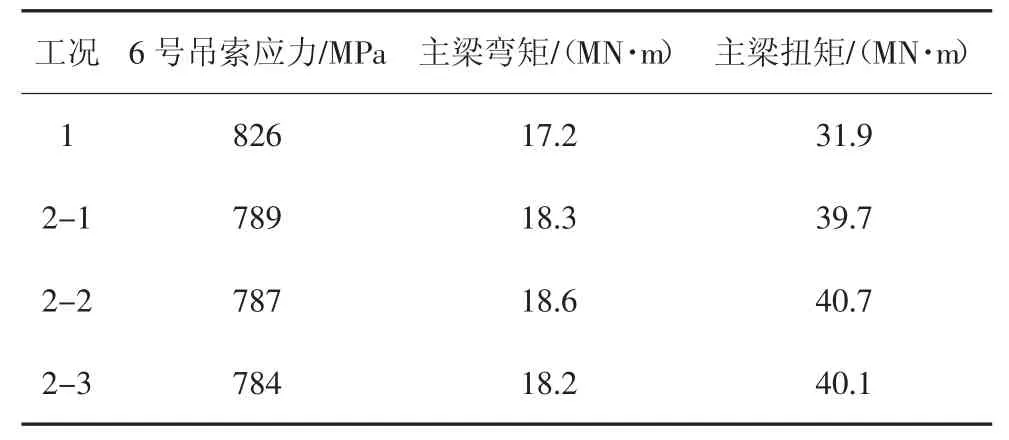
表1 7 号吊索在不同断索工况下结构动力响应极值Tab.1 Structural maximum responses subjected to the sudden breakage of hanger 7 with different scenarios

Δt 取0.001 s，采用突加荷载法和等效卸载法模拟7 号吊索断裂，图10 给出了断索后结构动力响应时程曲线.从图10 中可以看出，突加荷载法计算出的吊索应力和主梁扭矩极值大于等效卸载法计算结果，突加荷载法计算出的主梁弯矩最大值小于等效卸载法计算结果.如图10 所示，采用突加荷载法和等效卸载法计算出的吊索应力最大值分别为952 MPa 和826 MPa，主梁弯矩最大值分别为11.3 MN·m和17.2 MN·m，主梁扭矩分别为39.2 MN·m 和31.9 MN·m.结合表1 可以看出，等效卸载法与刚度退化法（工况1）计算结果相同.

3.2 Δt 和lrel（t）对结构响应动力效应的影响

为定量描述Δt 对结构响应动力效应的影响，定义动力放大系数（η），数学表达式为：

式中：S0表示断索前所关注构件内力（应力、剪力、弯矩或位移）；Sd表示断索后构件动力响应极值；Ss表示断索后结构处于稳定状态时构件内力.

在敏感性分析中，设定Δt 位于0.001 s 和10 s之间.采用刚度退化法（工况1）模拟7 号吊索断裂，图11 给出了断索持续时间与结构响应（相邻吊索应力、断索位置处主梁弯矩和扭矩）动力放大系数之间的关系.可以看出，动力放大系数随Δt 的增大而减小.相应的曲线变化规律可以划分为3 个阶段：Δt ＜0.01 s（1/240 的结构振动基本周期）时，η 的数值达到最大且几乎保持不变，结构响应的动力效应达到最大；Δt 从0.01 s 增加到1 s 时，η 急剧下降，结构响应动力效应随之减弱；Δt 大于＞1 s（2/5 的结构振动基本周期）时，η 逐渐接近于1，此时可忽略结构响应的动力效应.

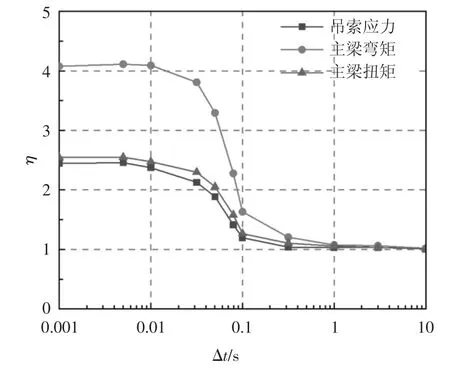
图11 断索持续时间与动力放大系数的关系Fig.11 Relation between Δt and DAF

采用等效卸载法模拟7 号吊索断裂，图12 给出了吊索拉力损失函数指数因子与结构响应动力放大系数之间的关系.从图12 可以看出，损失函数指数因子α 显著影响结构断索响应动力效应，并且影响程度与Δt 密切相关.α 取1 时，结构断索响应的动力效应最小.结构Δt＜0.01 s 时，α 对结构断索响应动力放大系数几乎没有影响；Δt 在0.01～0.1 s 之间时，α 对结构断索响应动力放大系数影响程度逐渐增强；当Δt 从0.1 s 增加到5 s 时，α 对结构断索响应动力放大系数影响程度逐渐减弱.如图12 所示，Δt 取0.1 s 时，随着α 从0.01 增加到10，吊索应力η 先从1.89 减小到1.24，再增加到2.24，主梁弯矩η 从3.42减小到1.75，随后增加到3.81，主梁扭矩η 先从2.19减小到1.33，再增加到2.34.

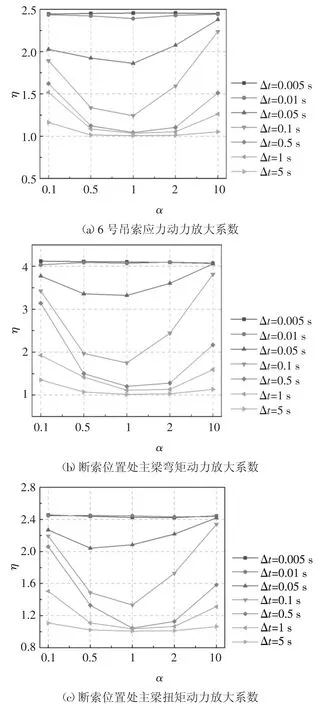
图12 吊索拉力损失函数指数因子与动力放大系数关系Fig.12 Relation between α and η

3.3 吊索断裂位置和根数对断索动力响应的影响

依据图8 中划分的工况，图13～图15 给出了吊索断裂位置和根数对结构动力响应的影响.图13 给出了不同位置单根吊索以及单边相邻两根吊索瞬间断裂后，剩余吊索应力最大值和动力放大系数.结果表明，长吊索（区域3 位置处吊索）应力最大值小于短吊索（区域1 或区域5 位置处吊索）应力最大值.两根吊索同时断裂比单根吊索断裂引起的吊索动力响应最大值有大幅度增长，但对应的动力放大系数有所下降.如图13（a）所示，单根吊索断裂后吊索应力最大值为738～900 MPa，单边相邻两根吊索同时断裂后，剩余吊索应力最大值为1 041～1 271 MPa.如图13（b）所示，单根吊索断裂引起吊索应力动力放大系数为2.2～2.55，两根吊索同时断裂引起吊索应力放大系数为2.12～2.25.

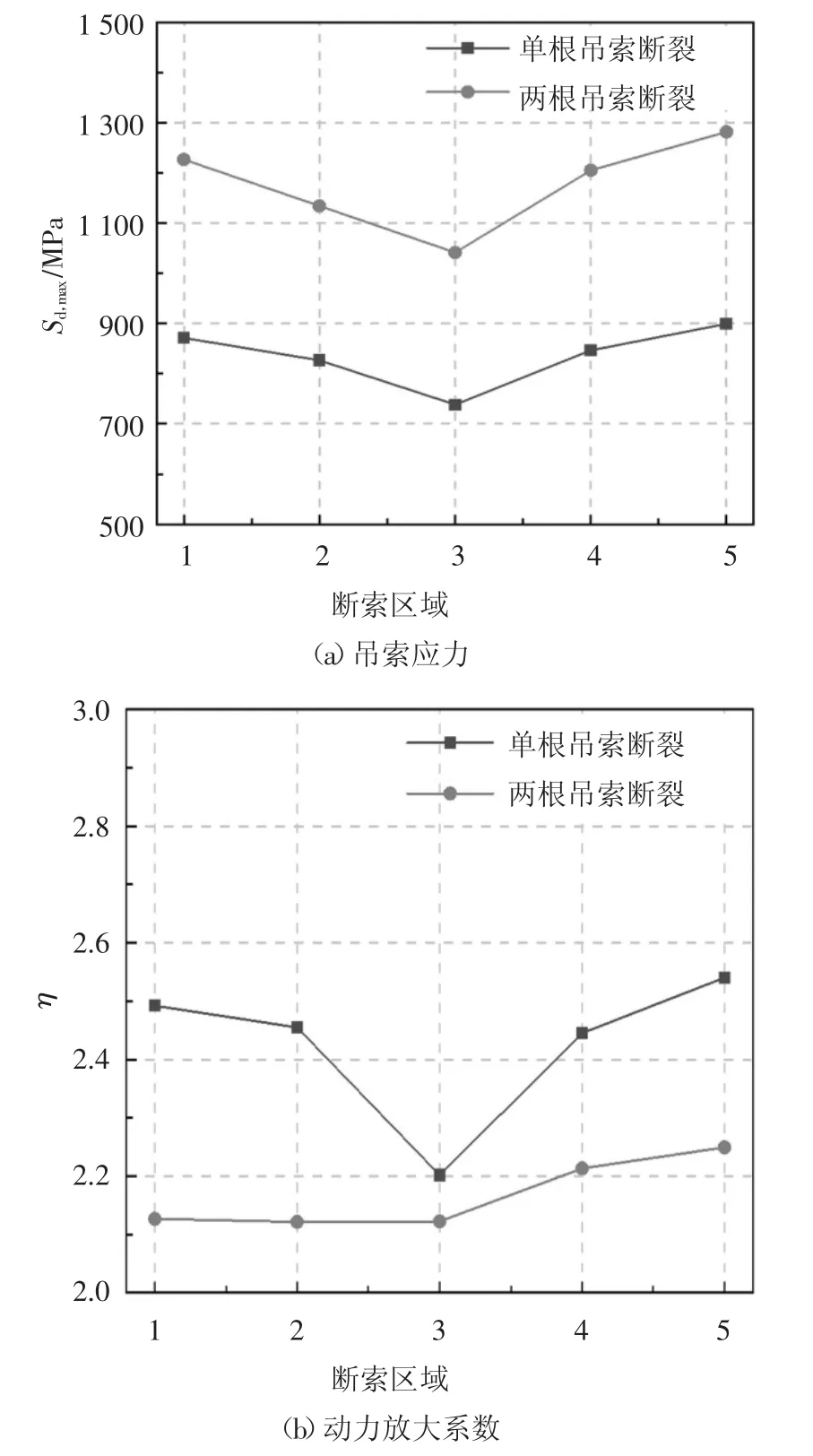
图13 断索根数和位置对吊索应力影响Fig.13 Relation between the number and location of the failed hanger the dynamic response of hangers'tensile stress

图14 为不同位置单根吊索以及单边相邻两根吊索瞬间断裂后，主梁弯矩极值和动力放大系数.结果表明，断索引起主梁弯矩动力放大系数波动剧烈，边跨跨中（区域2）和中跨跨中（区域5 处）位置处的吊索断裂后主梁弯矩较大.如图14（a）所示，区域2位置处，单根和两根吊索瞬间断裂引起的主梁弯矩极值分别为17.2 MN·m 和18.6 MN·m.区域5 位置处，单根和两根吊索瞬间断裂引起的主梁弯矩极值分别为16.6 MN·m 和32.3 MN·m.如图14（b）所示，单根吊索断裂后主梁弯矩动力放大系数在2.24～4.16 之间，两根吊索后主梁弯矩动力放大系数处于1.65～3.02 之间.

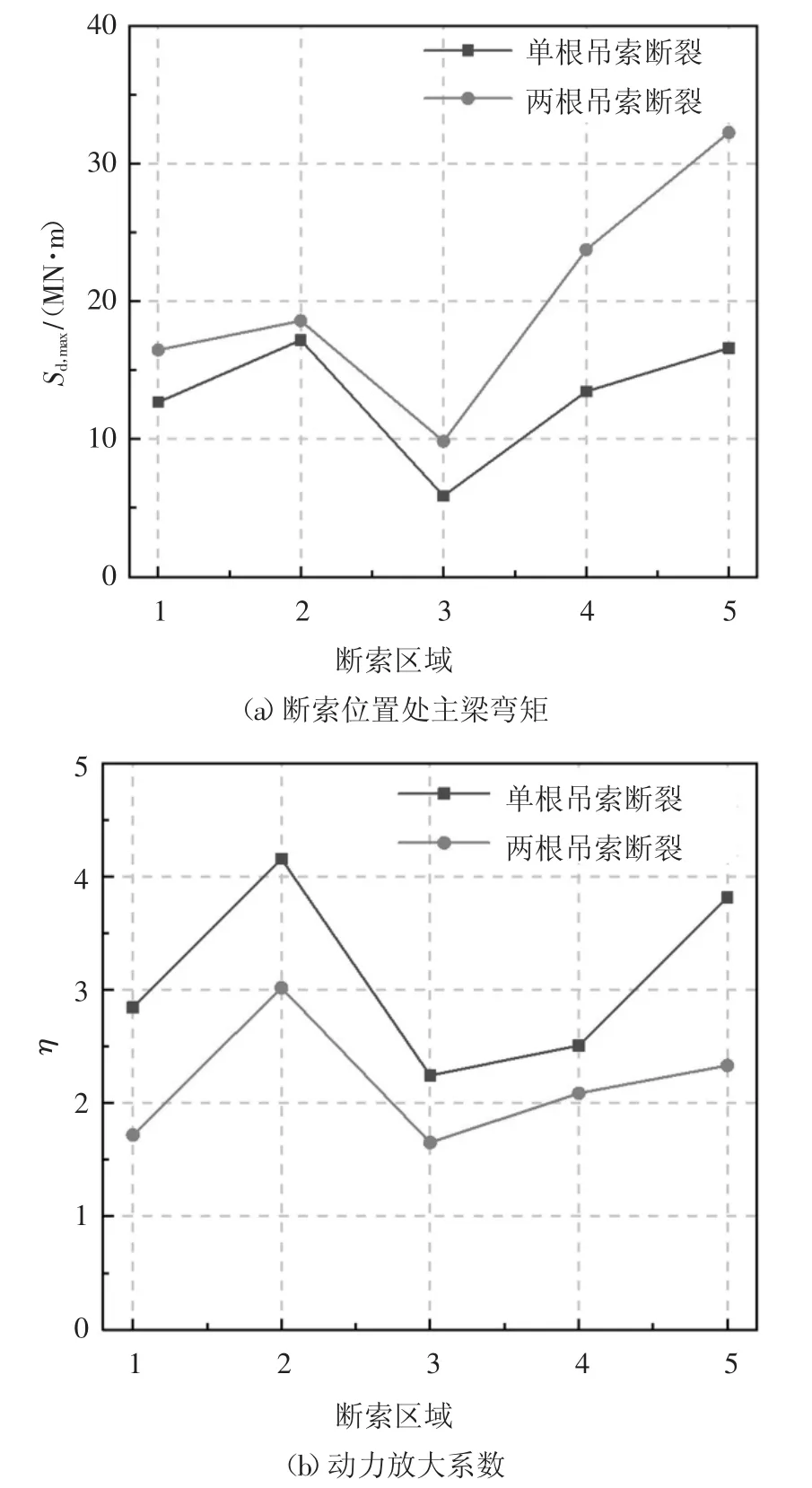
图14 断索根数和位置对主梁弯矩影响Fig.14 Relation between the number and location of the failed hanger and the dynamic response of girder's bending moment

图15 为不同位置单根吊索以及单边相邻两根吊索瞬间断裂后主梁扭矩极值和动力放大系数.结果表明，断索引起的主梁扭矩不可忽视，两根吊索同时断裂比单根吊索断裂引起的主梁扭矩最大值有大幅度增长.如图15（a）所示，单根吊索断裂后主梁最大弯矩为25.9～31.9 MN·m，两根吊索同时断裂后主梁最大弯矩为47.9～62.1 MN·m.如图15（b）所示，单根吊索断裂后主梁扭矩动力放大系数为2.02～2.43之间，两根吊索同时断裂后主梁弯矩动力放大系数为1.86～2.37 之间.

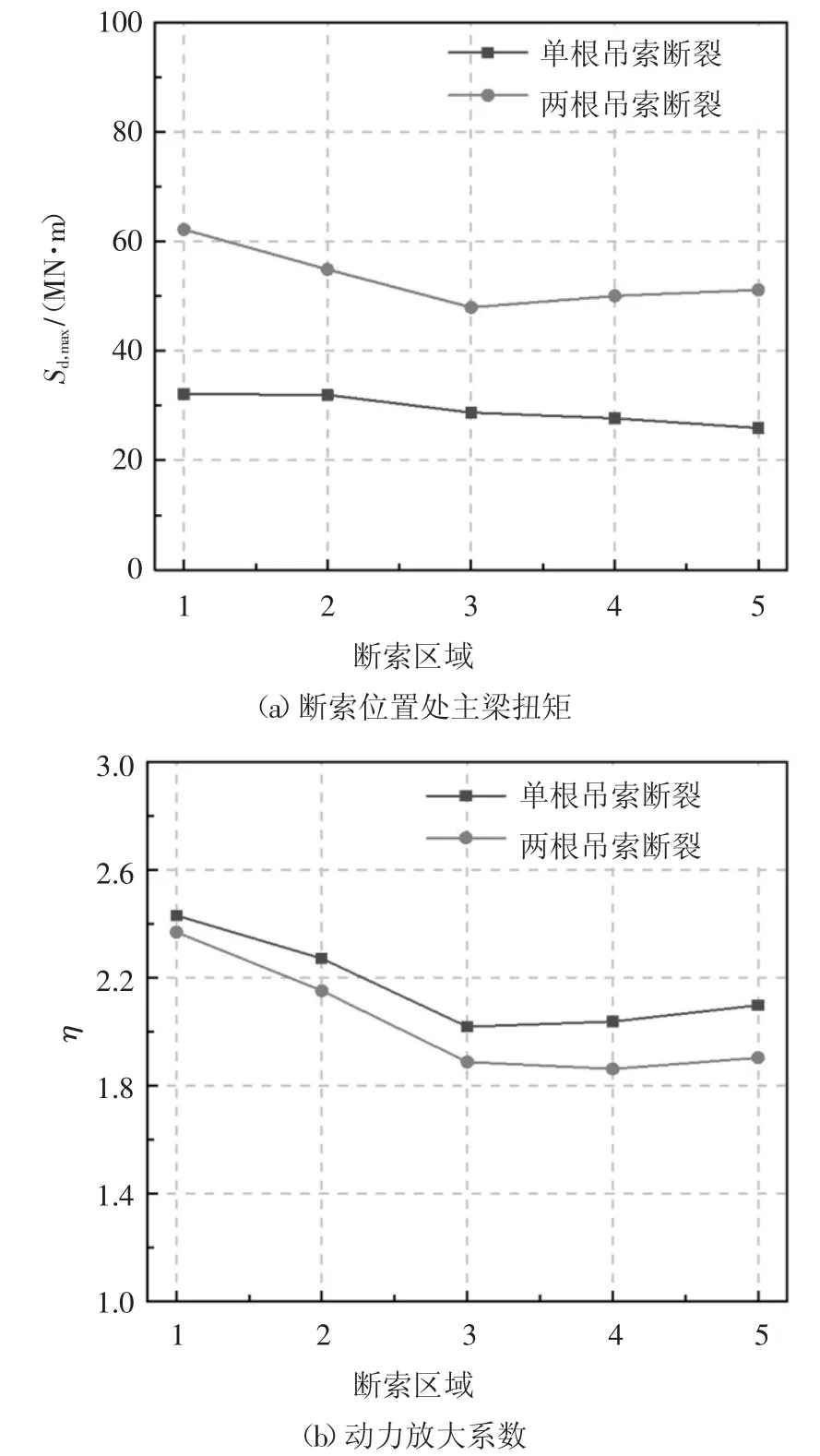
图15 断索根数和位置对主梁扭矩影响Fig.15 Relation between the number and location of the failed hanger and the girder’s torsional moment

4 结论

通过对悬索桥断索动力分析的有限元模拟方法展开研究，得到以下结论：

1）刚度退化法、突加荷载法和等效卸载法3 种模拟悬索桥吊索断裂过程的方法，每种方法都有其优点和局限性.进行悬索桥断索动力分析时，刚度退化法简单有效；等效卸载法既可真实反映断索前的结构状态，又可较好地捕获断索后结构响应；突加荷载法施加的外荷载需要多次迭代确定，分析模型中存在的断裂吊索对计算结果有一定影响.

2）悬索桥断索响应动力效应与Δt 以及lrel（t）密切相关.α 取1，吊索拉力损失函数是线性关系，结构断索响应动态效应最小.α ＜1 时，结构断索响应的动态效应最小值随着α 增加而减小.α ＞1 时，结构断索响应的动态效应最小值随着α 的增加而增加.吊索拉力损失函数为线性关系，Δt ＜0.01 s（1/240的结构振动基本周期）时，结构断索响应的动态效应达到最大且趋于稳定，Δt ＞1 s（2/5 的结构振动基本周期）时，结构响应的动态效应可忽略不计.

3）同一吊索断裂位置对结构动力响应的极值几乎没有影响，不同吊索断索位置和根数显著影响悬索桥的动力响应.单边相邻两根吊索同时断裂比单根吊索断裂引起的结构动力响应更加剧烈，但对应的结构响应动力放大系数有所降低.