大跨度斜拉桥下击暴流风致振动响应实测

刘志文，李书琼，刘勇，许映梅，陈政清

（1.风工程与桥梁工程湖南省重点实验室（湖南大学），湖南 长沙 410082；2.湖南大学 土木工程学院，湖南 长沙 410082；3.江苏苏通大桥有限责任公司，江苏 南通 226001;4.中铁第四勘察设计院集团有限公司，湖北 武汉 430063）

下击暴流是一种雷暴云中局部强下沉气流在到达地面后产生的直线型大风，在接近地面处风速达到最大，具有突发性、局部性和随机性等特点[1].我国是下击暴流多发国家之一，在全国较大范围内均有发生的可能性[2].下击暴流对工程结构影响较大，可能引起建筑结构、输电线塔、桥梁结构附属设施等破坏[3-5].因此，开展下击暴流风特性及其对工程结构影响的研究具有十分重要的意义.

国内外许多学者针对下击暴流风特性及其对结构的影响开展了大量的研究工作，主要工作有现场实测[6-9]、数值模拟[10-12]、风洞试验[13-18]和理论计算[19-22]等.在实测研究方面，Choi[6]在一座高为150 m 的塔上设置了5 个观测层，对50 多次雷暴的风速剖面进行了实测研究.Burlando 等[7]对2012 年10 月在意大利利沃诺科斯特观测到的一次下击暴流进行了风场特性分析.Solari 等[8]对地中海北部港口6 年间发生的277 个下击暴流风速记录进行了系统分析，获得了下击暴流风特性.Stengel 等[9]对德国北部的一条输电线路进行实测，观测到悬索塔导线在一次下击暴流下的实测响应，并与有限元模型的时域模拟进行了比较.在数值模拟研究方面，Wood 等[10]进行了基于湍流模型的下击暴流计算流体力学数值模拟，其结果与下击暴流喷射装置试验结果吻合较好.Chay等[11]采用CFD 数值模拟方法模拟了下击暴流平均风，重点考察了风速随下击暴流成熟和衰减强度的变化规律.刘志文等[12]采用二维数值模拟方法在边界层风洞中设置倾斜平板进行了数值模拟研究，结果表明边界层风洞中设置倾斜平板可有效模拟下击暴流水平风速剖面.在试验研究方面，曹曙阳等[13]在日本宫崎大学大型多风扇主动控制风洞中实现了雷暴冲击风模拟.Jesson 等[14]为研究建筑结构在下击暴流瞬态气流作用下的压力分布，研发了下击暴流瞬态风场模拟试验装置，其试验结果表明采用该装置模拟的瞬态风速时程与实测下击暴流瞬态风速时程吻合较好.Aboutabikh 等[15]设计并制造了两层带叶片的百叶窗下击暴流模拟试验装置，在风洞中模拟了下击暴流风场.辛亚兵等[16]基于传统大气边界层风洞开发了下击暴流模拟装置，并对下击暴流风作用下大跨连续刚构桥最大双悬臂状态风致振动响应进行了试验研究.Elawady 等[17]采用WindEEE 多功能风洞模拟了下击暴流风场，并进行了多跨输电线路下击暴流风致振动响应气弹模型风洞试验研究.Junayed 等[18]采用WindEEE 多功能风洞模拟了缩尺比较大的下击暴流风场特性，并将试验模拟的下击暴流平均风场和脉动风场特性与实测下击暴流风特性进行了比较，两者吻合相对较好.在理论计算方面，Chen 等[19]提出了一种混合随机模型模拟下击暴流风速时程，即下击暴流平均风由Wood 风剖面和Holmes 时间函数得到，脉动风速由随时间变化的幅值调幅函数和服从标准正态分布的高斯随机过程得到.Hao 等[20]采用基于冲击射流模型的CFD 数值仿真技术模拟了下击暴流稳态风场和瞬态风场，分析了桥梁在模拟下击暴流作用下抖振时域响应，结果表明，下击暴流脉动风速对桥梁响应影响相对较小.辛亚兵等[21]以赤石大桥桥址处实测下击暴流风时程数据为基础，采用谐波叠加法模拟桥址区脉动风速并加以调制，实现了桥址区下击暴流风时程模拟，对下击暴流作用下大跨度斜拉桥施工状态静风响应和非线性时域抖振响应进行了计算.

综上所述，目前国内外学者对下击暴流风场特性的观测与试验研究相对较多，而对下击暴流作用下的结构响应现场实测研究则相对较少，因此进行下击暴流风特性及其风致振动响应实测研究具有十分重要的价值和意义.本文依托苏通大桥风致振动监测系统，对大跨度斜拉桥风致振动响应特性进行为期2 年的现场实测研究，监测到2019 年4 月19日桥位处发生了一次突发大风，监测系统完整记录了本次突发大风风速、风向及主梁振动加速度响应数据，为大跨度斜拉桥下击暴流风效应研究积累了十分宝贵的实测数据.本文重点对本次下击暴流大风的风特性与主梁风致振动响应特性进行分析.

1 苏通大桥风致振动监测系统

苏通长江公路大桥位于江苏省南通市和苏州市之间，是国家重点干线公路沈海高速（G1）跨越长江的重要通道.据设计资料可知苏通大桥主桥为主跨1 088 m 的双塔双索面斜拉桥，其跨径布置为100 m+100 m+300 m+1 088 m+300 m+100 m+100 m=2 088 m.主梁采用闭口流线型钢箱梁，梁宽41.0 m，梁高4.0 m；斜拉索最大长度为577 m；采用倒Y 形桥塔，塔高300.4 m.考虑到大桥规模与运营期内的维护需要，该桥建成后安装了结构健康监测系统（Structural Health Monitoring System，SHMS）[23].该系统可对风、温度、车辆荷载及腐蚀作用等进行监测，并对桥梁结构的位移、索塔和桥墩倾斜度、支座位移、拉索索力和结构应变等进行监测.

为确保大桥在风荷载作用下安全运营，在苏通大桥结构健康监测系统基础上，建立了苏通大桥风致振动监测系统，对大桥部分拉索锚固处主梁竖向、横向振动加速度响应进行监测.风速仪布置于主桥南、北塔塔顶，主跨跨中桥面上、下游距离桥面2.28 m 高度处.风向角0°对应北风，90°对应东风，采样频率为1 Hz（实际测量中开启二维模式，只采集水平风速、风向），由于苏通大桥桥轴线与正北方向有10.6°偏角，故需对风向角进行修正以得到以桥轴线为参考的风偏角.在主梁上NJ26D 与NJ32D 号拉索锚固处分别布置了竖向和横桥向加速度传感器（型号为941B），以监测主梁竖向与横桥向振动加速度响应，采样频率设置为100 Hz.图1 所示为苏通大桥风致振动响应监测系统传感器布置示意图，图2 所示为苏通大桥主梁横断面及风速仪位置示意图.

图1 苏通大桥风致振动监测系统（单位：m）Fig.1 Wind-induced vibration monitoring system of STB（unit：m）

图2 主梁标准断面图（单位：mm）Fig.2 Cross section of main girder（unit：mm）

2 桥址处风特性分析

2.1 风速风向时程

2019 年4 月19 日，苏通大桥桥位处出现了一次显著的大风天气.图3 所示为苏通大桥风致振动监测系统所记录的主跨跨中桥面上、下游及桥塔塔顶处风速风向时程.表1 所示为各风速监测点位置风速突变时刻风速、风向参数统计汇总.结合图3 及表1 结果可知，在4 月19 日中午12：19 时，南塔塔顶风速首先达到最大瞬时风速60.5 m/s；在12：55 北塔塔顶风速出现最大瞬时风速62.9 m/s；12：57—12：58时主跨跨中桥面下游、上游风速分别达到最大值32.4 m/s 和27.3 m/s；各监测点处突变大风持续时间约为10～24 min，与文献[24]所给出的单个微下击暴流平均持续时间约为13 min 较为接近；在下击暴流发生前较长时间内，主跨跨中主梁上、下游侧及南北塔塔顶的风向变化趋势基本一致，即由南风变为西风，并在较长时间内风向保持不变，在下击暴流发生时段内各监测点风向发生了较为明显的突变.综合以上现象可看出，本次大风天气具备下击暴流的气象特征，初步判断应为一次下击暴流.

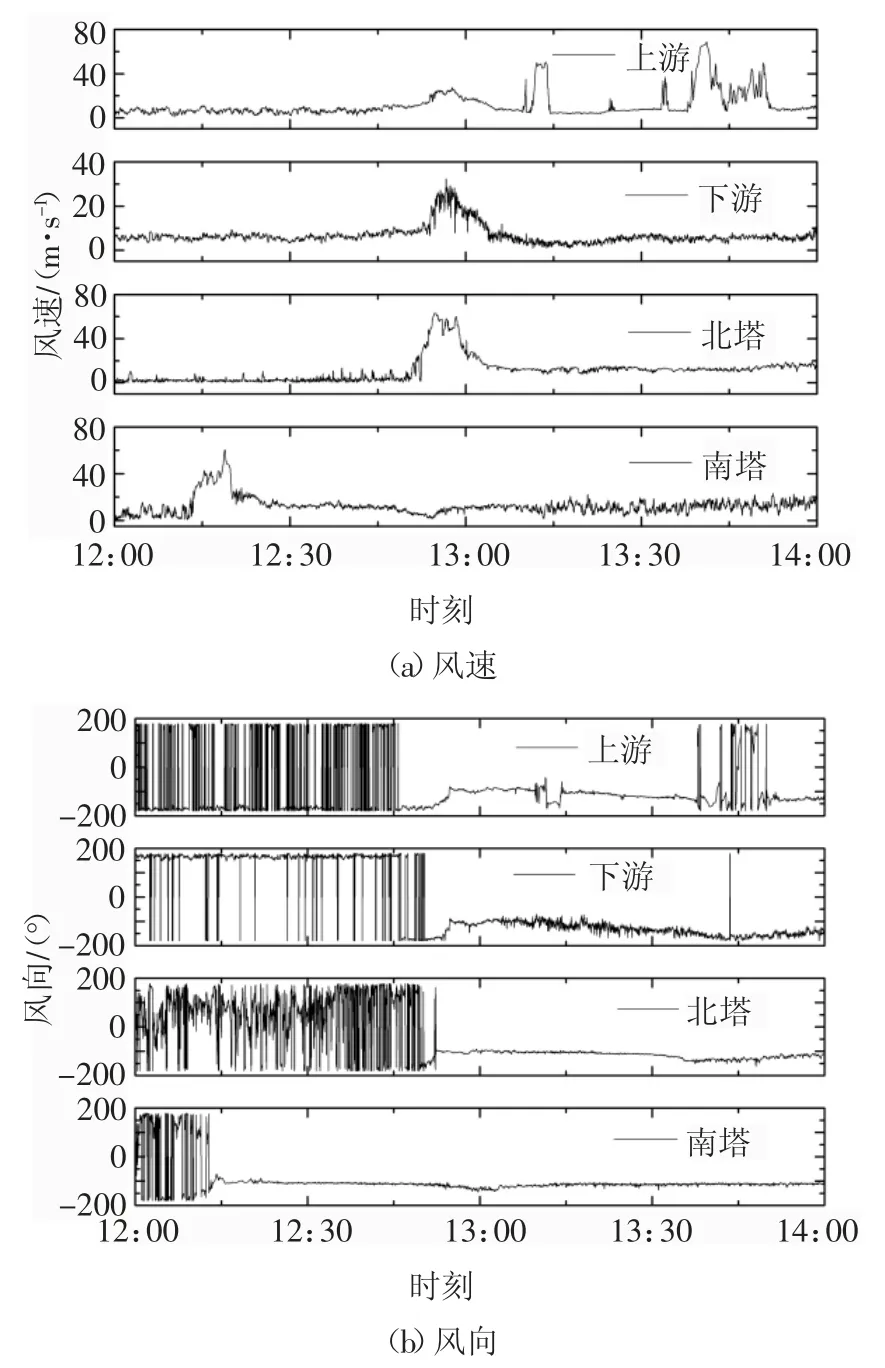
图3 主跨桥面处及桥塔塔顶风速、风向时程曲线（2019 年4 月9 日）Fig.3 Time histories of wind speeds and yaw angles at the mid-span girder level and pylon top（Apr.9，2019）

由表1 可知，大桥不同监测点处风速开始突变时刻以及峰值时刻存在较大差异，南塔出现下击暴流时刻较其他测点要提前30 min，其原因可能是此次下击暴流的尺度较小，影响范围有限，且其中心可能处于移动中.由图3 中风向与表1 中时间参数可以推断出，4 月9 日出现的下击暴流位于苏通大桥上游侧，且其中心自南向北缓慢移动.

表1 2019 年4 月19 日苏通大桥关键位置风特性参数Tab.1 Wind characteristics at key points of STB on Apr.19，2019

依据图3 中风速可知，主梁上游风速在13：13以及13：45 均存在特异性大风，此时风速可达68 m/s，远大于下击暴流峰值风速.结合上游风向时程可看到，上述2 个时刻风向突然转变，由-100°（垂直于桥轴向）突变至-168.6°与179.1°（基本沿着桥轴向）.可以判断出，这2 个时刻存在着沿桥轴线方向的强局部气流对上游风速造成干扰，并且其流向与桥轴线平行，故未对下游风速产生影响.此外，也不排除13：10 之后仪器出现短暂故障，具体原因有待进一步研究.本文重点研究12：49—13：09 发生的下击暴流风特性，故此次特异数据基本没有影响.同时为了保证数据的真实可靠以及对比不同高度处下击暴流风特性，后文主要对主梁下游以及北塔塔顶风速进行分析.

2.2 时变平均风与脉动风速

由图3 可知，在下击暴流时段主跨跨中主梁处、桥塔塔顶等风速为非平稳风速时程，故参考文献[25-26] 中瞬态风信号的经典分解规则.将瞬时风速U（t）分解为时变平均风速与非平稳脉动风速u（t）：

脉动风速u（t）为一非平稳随机过程，可表示为

式中：u′（t）为折减脉动风速，即为平稳高斯随机过程；σu（t）为脉动风速u（t）的缓变根方差，即

即

式中：Iu（t）为时变湍流度.

为进一步研究下击暴流作用下主跨跨中桥面高度处以及桥塔顶部高度处的风速特性，需要对其进行风速分解.其中时变平均风速的提取采用文献[25]中的滑动平均法，滑动平均风速定义如下：

式中：Urm（j）为j 时刻的瞬时风速；Trm为滑动平均的时间间隔，结合文献[7]中Burlando 的建议取值，本文中Trm=30 s.

图4 所示分别为下击暴流作用下苏通大桥主跨跨中桥面高度处下游与北塔塔顶的时变平均风速和脉动风速分析结果.

图4 实测突变风样本时变平均风速和脉动风速Fig.4 Time-varying average wind speed and fluctuating wind speed of the abrupt wind samples measured

由图4（a）（b）对比可知，在下击暴流时段，北塔塔顶的时变平均风速比主跨跨中桥面下游侧时变平均风速变化更为剧烈，且塔顶风速在下击暴流出现后平均风速比发生前增大数倍.两者的脉动风速变化规律也显著不同，主梁跨中下游侧在下击暴流出现前脉动风速低，当其过境时脉动风速峰值为13.7 m/s，过境后脉动风速仍保持较大值；北塔塔顶脉动风速变化却与之相反，下击暴流出现前脉动风速已达10 m/s 以上，下击暴流发生时达到16.2 m/s，过境后反而较低.可以看到下击暴流对苏通大桥不同高度处风特性的影响存在较大差异.

除下击暴流风速突变特征外，下击暴流作用下主梁下游与北塔塔顶的风向变化规律也值得进一步分析.故采用与式（5）一致的滑动平均法求取30 s 时变平均风向，图5 所示为下击暴流作用下苏通大桥主梁下游与北塔塔顶的瞬时风向和时变平均风向.由图5 可知，下击暴流发生前主梁下游主导风向约165°，北塔风向波动剧烈；下游风向突变后稳定至-96°～-110°，北塔风向为-100°，基本垂直于桥轴线；下击暴流衰退后，下游瞬时风向与时变平均风向差异显著，北塔风向保持稳定.此次下击暴流未发生时风向变化剧烈，发生时风向稳定，发生后不同高度处风向变化规律不同.

图5 实测瞬时风向和时变平均风向Fig.5 Measured instantaneous wind direction and time-varying average wind direction

2.3 湍流度

湍流度是描述脉动风速变化大小的一个重要的参数，为脉动风速根方差与平均风速之比.考虑到下击暴流时空尺度小，具有突发性，且持续时间短暂，参考文献[7]中处理方法，选取时距30 s 采用式（4）计算湍流度.为便于比较，针对下击暴流时段风速分别取平均时距为T1=30 s 和T2=10 min 进行顺风向湍流度计算，图6 所示为主跨跨中主梁高度处下游与北塔塔顶处湍流度随时间变化曲线.

由图6 可知，当取平均时距为T1=30 s 时，在下击暴流时段主跨跨中桥面高度处下游侧顺风向湍流度约为Iu（t）=0.048～0.32，北塔塔顶湍流度约为Iu（t）=0.01～0.014.当取平均时距为T2=10 min 时，在下击暴流时段主跨跨中桥面高度处下游侧顺风向湍流度约为Iu（t）=0.43～0.51，北塔塔顶湍流度约为Iu（t）=0.31～0.48.而文献[27]中台风作用下苏通大桥主梁高度处湍流度为0.10～0.30，可见下击暴流作用下主梁高度处湍流度总体上略大于台风作用下的湍流度.主要原因是下击暴流风速突变较台风而言持续时间短且突变风速较大.

图6 主梁下游侧及北塔塔顶湍流度Fig.6 Turbulence intensity at leeward of main girder and north pylon top

2.4 折减脉动风特性

由上文可知下击暴流风场中的脉动分量与常规台风气象差距较大，现着重对其脉动分量进行研究.仍以30 s 为基本时距，利用式（2）计算下击暴流过境时主跨跨中主梁桥面高度处下游与北塔塔顶处时变风速中的折减脉动风速成分，绘制折减脉动风速随时间变化曲线如图7（a）（d）所示.由图7 可知，折减脉动风速呈现出经典随机平稳高斯特性.通过图7（b）（e）的频率直方图可见，虽然偏斜度不完全为0，峰度不为3，但是图形与参考高斯拟合曲线有良好的一致性，证实了这两个测点的折减脉动风的高斯特性.按式（6）计算折减脉动风速的概率密度p（u′）.

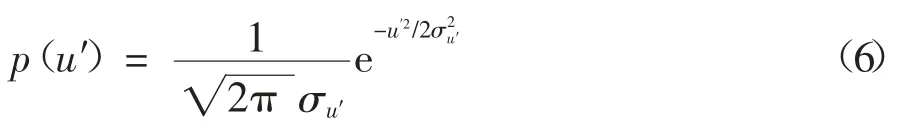
式中：u′为脉动风速；σu′表示脉动风速标准差.为研究折减脉动风速的频率成分特征，将实测顺风向脉动风谱与Von-Karman 谱、Davenport 谱、Simiu 谱进行对比.

Von-Karman 谱是1948 年美国著名空气动力学专家Von-Karman 提出的自由大气水平脉动风谱：

Davenport 谱是1961 年加拿大著名风工程专家Davenport 提出的自由大气水平脉动风谱：

式中：f=1 200 n/U（10），U（10）是z=10 m 高度处的平均风速.

Simiu 谱为1974 年美国学者Simiu 提出的与高度有关的水平脉动风速谱：

式中：f=nz/u（z），其中z 为测点高度.

由图7（c）（f）可见，跨中桥面高度处下游与北塔塔顶的折减脉动风速功率谱趋势相同.对比实测谱线与经验谱线可知，3 种经验谱线与实测谱总体趋势一致，但Davenport 谱与实测谱线在低频段拟合较好，高频差异较大；Simiu 谱相反，低频差异大，高频吻合度高；Von-Karman 谱曲线变化介于两者之间.出现这种现象的原因主要是下击暴流风自身的非平稳特性、数据处理时采用非平稳风速分解模型以及各经验谱的特有参数与适用性的差异.

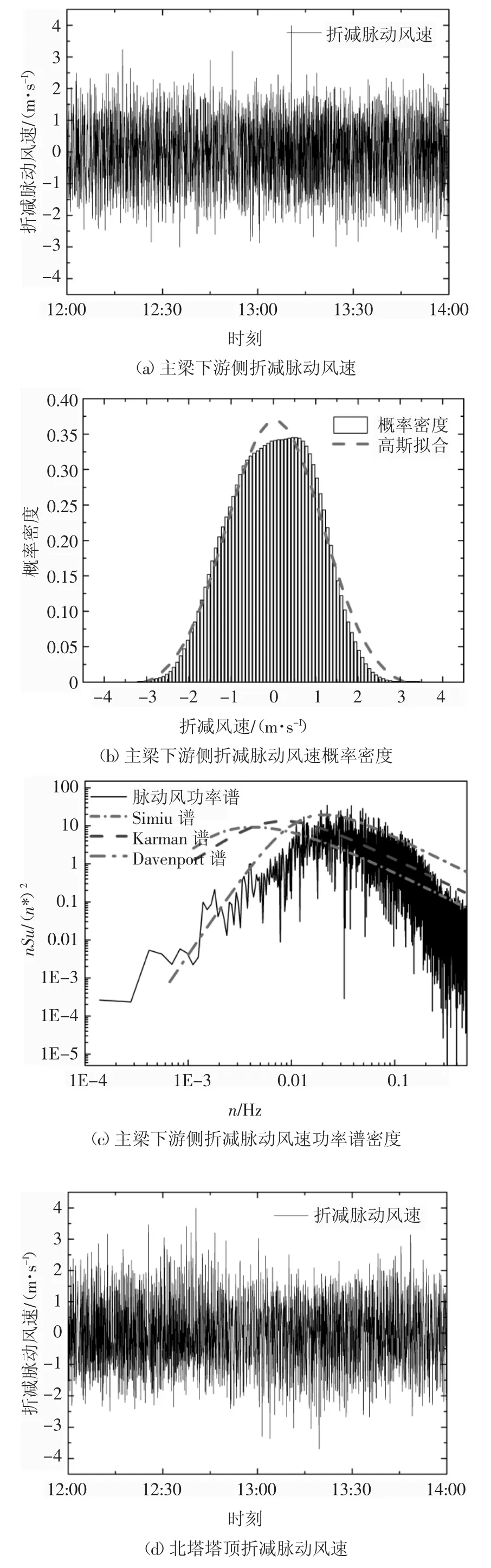
图7 主梁下游侧与北塔塔顶处折减脉动风特性Fig.7 Reduced fluctuating wind characteristics at leeward of the main girder and north pylon top

本文中实测谱线与文献[7] 中Burlando 等在2012 年观测到的意大利利沃诺海岸遭遇的下击暴流风场下的折减脉动风速功率谱密度函数曲线相比，两者功率谱在曲线的变化趋势以及峰值大小上具有较好的相似性.且两者低频段均较低，下降段符合经典的天气型风惯性子区间的n-5/3斜率下降.

3 主梁振动响应

3.1 主梁加速度响应时程

为研究苏通大桥主梁在风荷载作用下的振动特性，以保证大桥在运营期间安全运行，分别在NJ32D与NJ26D 号拉索与主梁锚固处安装加速度传感器，监测主梁竖向、横桥向加速度响应.图8 所示为2019年4 月19 日12：00—14：00 主梁在NJ32D、NJ26D拉索锚固处竖向、横桥向加速度响应时程曲线.

由图8 可知，NJ32D 和NJ26D 号拉索锚固处主梁在该日中午12：49—13：09 附近均发生了一次加速度响应较大的短时振动现象，主梁在NJ32D 拉索锚固处的加速度响应与主梁在NJ26D 拉索锚固处的加速度响应总体较为接近；主梁在这两处的竖向和横桥向最大加速度响应幅值分别约为0.25 m/s2和0.10 m/s2，主梁竖向加速度响应幅值约为横桥向加速度响应幅值的2.5 倍.

图8 主梁跨中附近竖向与横桥向加速度响应Fig.8 Vertical and horizontal acceleration responses at mid of the main girder

为进一步了解下击暴流发生时主梁结构振动响应特征，对12：49—13：09 时段主梁在NJ32D 和NJ26D 拉索锚固处的振动加速度响应进行时频分析.考虑到下击暴流作用下的结构振动响应具有明显非平稳性，故本文采用可考虑信号时变特性的连续小波变换分析方法对主梁振动响应进行分析.

在小波变换中，一组形状相似的小波基函数是由母小波经过伸缩与移动进行转化后得到的.任意信号Ψ（t）的小波变换就是把信号Ψ（t）以小波函数为基底将其展开，再把信号以小波函数的线性组合表示出来.对于任意信号Ψ（t）∈L2（R）（其中L2（R）为能量有限的信号空间），Ψ（t）的傅里叶变换为当满足条件：

时，则称Ψ（t）为一个基本小波或母小波，同时将Ψ（t）经过平移与伸缩后可以得到：称其为一个小波系列，称a 为伸缩因子，b 为平移因子.

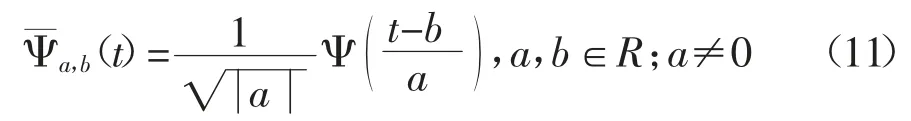
任意信号f（t）（f（t）∈I2（R））的连续小波变换（Continue Wavelet Transform，CWT）表达式为：

采用MATLAB 中小波工具箱对主梁振动加速度数据做连续小波变换并绘制时频图.选取CMOR小波为小波基函数，其中参数定义：带宽fb=1.5 Hz，中心频率fc=3 Hz.图9、图10 分别所示为NJ32D、NJ26D 锚固处下击暴流作用时段主梁竖向、横桥向加速度响应不同时刻频谱特征.

图9 NJ32D 锚固处主梁加速度时频特征Fig.9 Amplitude spectra of the accelerations of the main girder at anchorage of NJ32D stay cable

同时为进一步分析下击暴流作用下苏通大桥的振动模态，使用有限元计算软件ANSYS 建立全桥有限元模型进行动力特性分析，表2 所示为苏通大桥主桥结构成桥状态动力特性分析结果汇总.由表2及图9 可知，下击暴流发生时段主梁在NJ32D 号拉索锚固处竖向振动加速度响应主频为0.183 Hz，与苏通大桥主桥结构成桥状态一阶正对称竖弯频率f3=0.174 4 Hz 较为接近；由图10 可知，下击暴流发生时段主梁NJ26D 号拉索锚固处竖向振动加速度响应主频为0.183 Hz 和0.217 Hz，与苏通大桥主桥结构成桥状态主梁一阶正对称竖弯频率f3=0.177 4 Hz 和主梁结构一阶反对称竖弯频率f4=0.214 6 Hz 接近.综合表2 及图9～图10 可知，主梁在NJ32D 和NJ26D处横桥向振动加速度响应主频均为0.116 7 Hz，与主梁一阶正对称侧弯频率f2=0.097 5 Hz 较为接近.综上可知，在下击暴流风作用下，主梁竖向振动响应明显大于横桥向振动响应，且均以低阶竖弯振型为主.

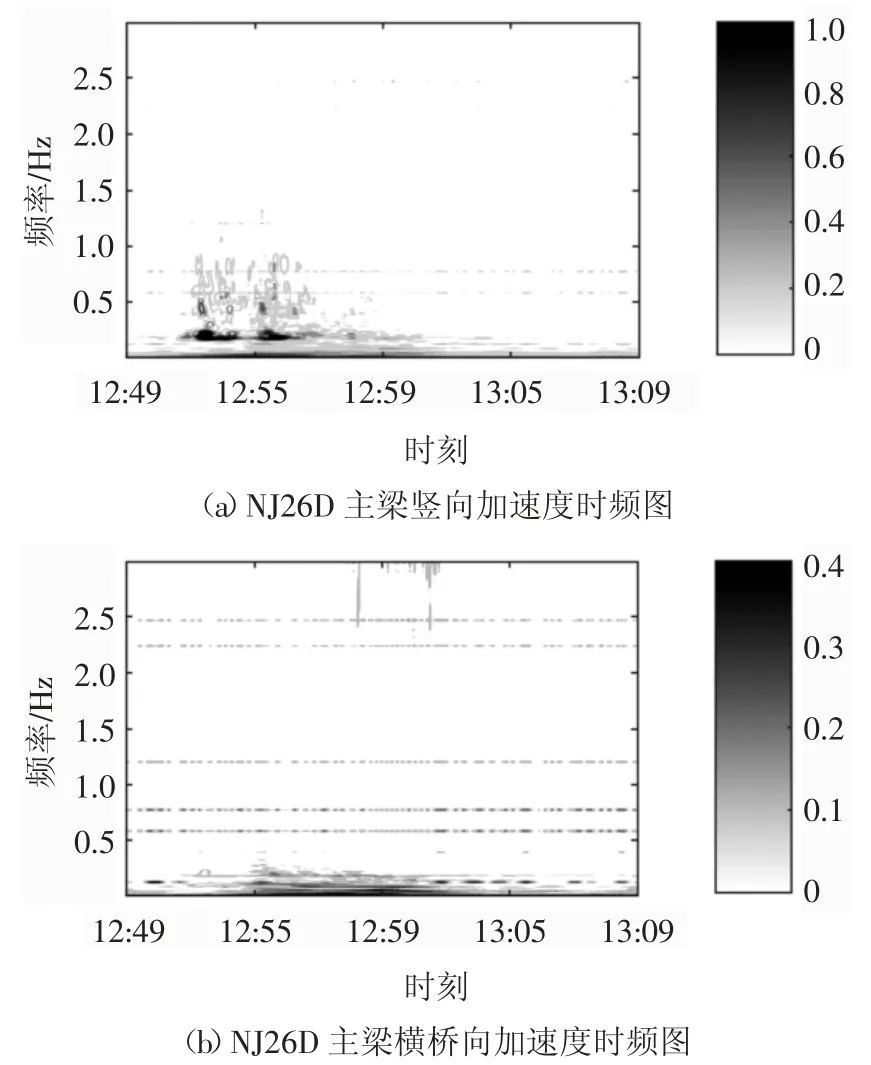
图10 NJ26D 锚固处主梁加速度时频特征Fig.10 Amplitude spectra of the accelerations of the main girder at anchorage of NJ26D stay cable

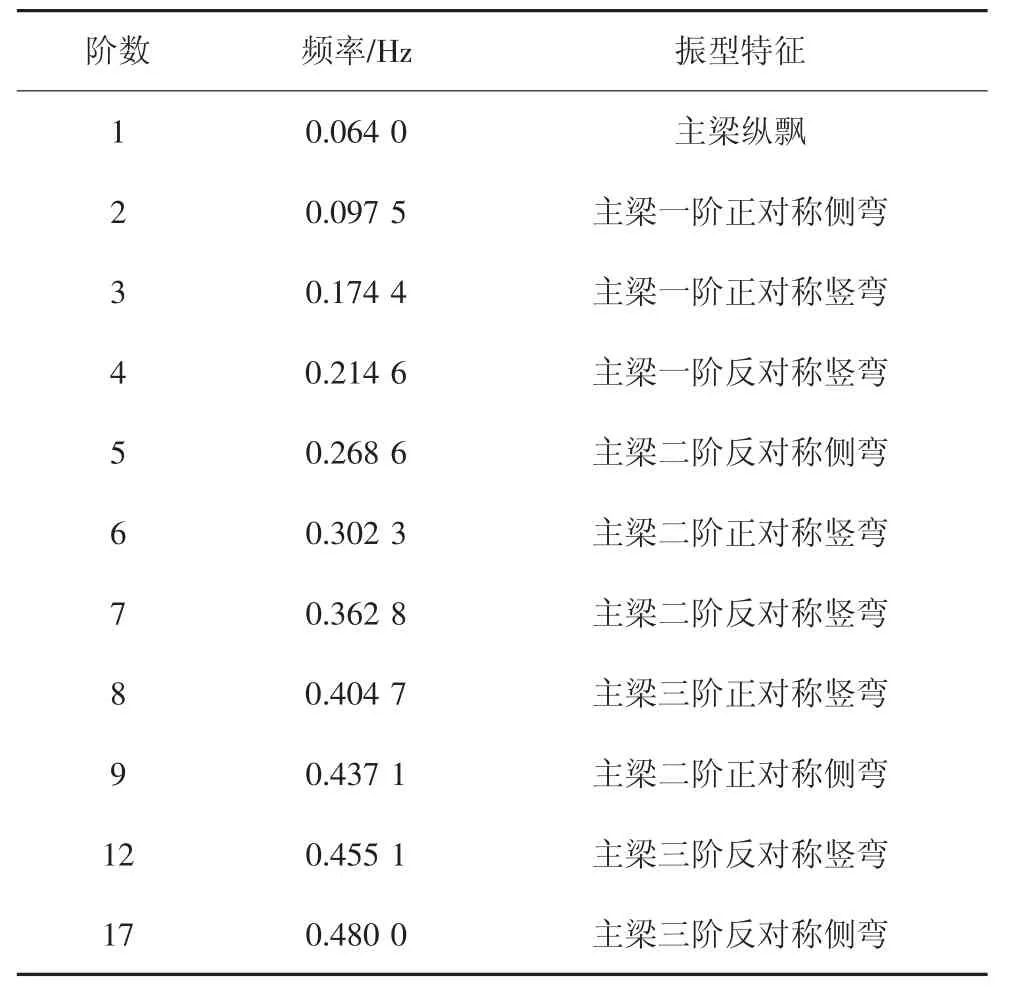
表2 苏通大桥成桥状态结构动力特性分析结果Tab.2 Structural dynamic characteristics of STB in service state

3.2 主梁位移响应

考虑到主梁竖向、横向加速度响应以低频为主，故对主梁加速度响应时程进行积分，以得到主梁竖向、横桥向位移响应时程.由逆傅里叶变换公式，可将任意频率下的加速度信号的傅里叶分量表示为：

式中：a（t）为加速度信号在频率ω 的傅里叶分量；A为对应a（t）的系数；j 为虚数，即

当初速度与初位移分量均为0 时，对加速度信号的傅里叶分量两次积分可得出位移分量：

式中：x（t）为速度信号在频率ω 的傅里叶分量；X 为对应x（t）的系数.

计算加速度信号的二次积分的数值公式为：

式中：fd和fu分别为下限截止频率与上限截至频率，Hz，此处取fd=0.1 Hz、fu=50 Hz；X（k）为x（r）的傅里叶变换；Δf 为频率分辨率，Hz.

图11 所示为采用该方法所计算得到的主梁在NJ32D 拉索、NJ26D 拉索锚固处的竖向和横桥向位移响应时程曲线.由图11 可知，在下击暴流时段，主梁在NJ32D 拉索锚固处竖向和横桥向位移响应最大幅值分别为0.111 m 和0.027 m；主梁在NJ26D 拉索锚固处竖向和横桥向位移响应最大幅值分别为0.116 m 和0.020 m.可见在下击暴流作用下，主桥结构主梁振动响应明显增大.

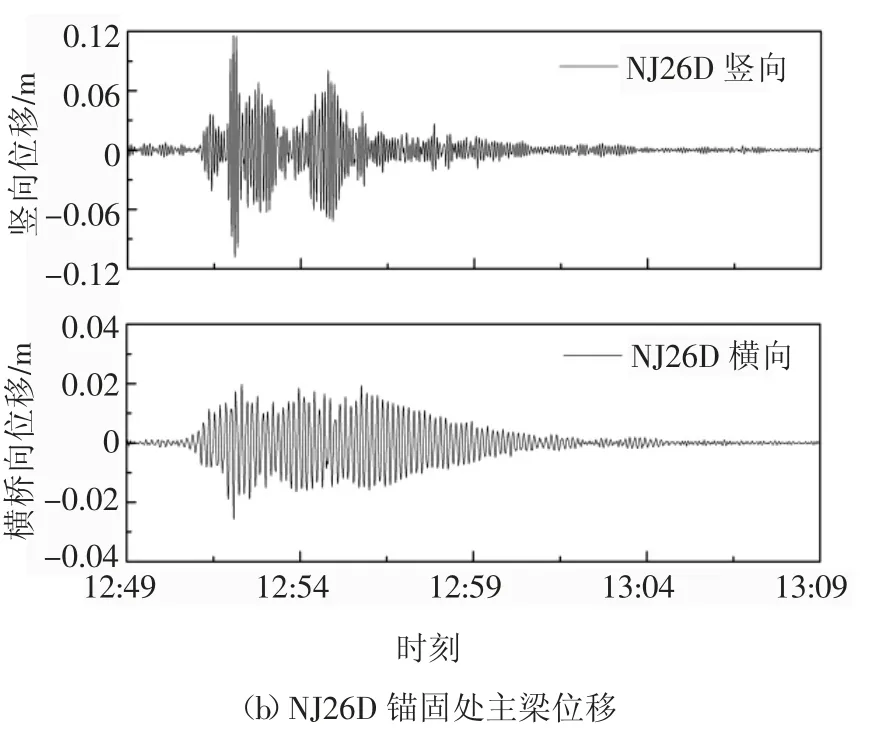
图11 主梁主跨跨中附近竖向、横桥向位移响应时程Fig.11 Time histories of the vertical and lateral displacements at the mid of the main deck

4 结论

依托苏通大桥结构健康监测系统和风致振动响应监测系统，对2019 年4 月19 日的一次突发大风风速、风向和主梁风致振动加速度响应数据进行分析，得到如下主要结论：

1）2019 年4 月19 日12：19，苏通大桥桥位处出现了瞬时突发大风，南塔、北塔塔顶最大瞬时风速分别为60.5 m/s 和62.9 m/s，主跨跨中桥面高度处下游、上游侧最大瞬时风速分别为32.4 m/s 和27.3 m/s，突变大风持续时间约为10～24 min；各监测点风向存在较为明显的突变现象；不同监测点处风速最大值达到时刻存在一定差别，初步判断该突发大风应为一次下击暴流现象.

2）在下击暴流时段（约在13：00 左右），当取平均时距为T1=30 s 时，主跨跨中桥面高度处下游侧顺风向湍流度约为Iu（t）=0.048～0.32，北塔塔顶顺风向湍流度约为Iu（t）=0.01～0.014；当取平均时距为T2=10 min 时，下击暴流时段内主跨跨中桥面高度处下游侧顺风向湍流度约为Iu（t）=0.43～0.51，北塔塔顶顺风向湍流度约为Iu（t）=0.31～0.48.主梁下游与北塔塔顶处折减脉动风速符合高斯特性，其功率谱与Burlando 等学者[7]的实测结果吻合较好.

3）在下击暴流作用下，苏通大桥主梁主跨跨中竖向振动响应明显大于横桥向振动响应，且均以低阶振动响应为主.主梁竖向位移约0.12 m，横桥向位移0.03 m，下击暴流作用下大跨度斜拉桥主梁振动响应明显增大.