改进的频繁模式挖掘算法*

魏 坤 王 芳 黄树成

（江苏科技大学计算机学院 镇江 212001）

1 引言

数据挖掘，也称为数据中的知识发现，用于发现隐藏在大型数据库中的知识模式［1］。许多数据挖掘方法被用来提取有趣的东西，比如从庞大的数据中获取关联规则。关联规则挖掘是搜索给定数据集中项之间的关联关系，即本质是对频繁模式的挖掘。频繁项集挖掘是大多数数据挖掘应用程序中的经典问题之一［2］。

提取频繁项集的算法有很多，两种主要的算法是Apriori和FP-Growth［3］。Apriori是一种典型的事务数据库频繁项集挖掘和关联规则发现的算法，然而，挖掘过程中多次数据库扫描引起大量I/O开销［4］。FP-Growth是一种基于树的频繁项集挖掘算法，它以一种分而治之的方式工作，这种方式可以在很大程度上减小后续条件FP树的大小，它仅需对数据集进行两次扫描［5］。FP树是事务的压缩表示，然而，并不减少候选项集的潜在组合数，这是FP增长的瓶颈。此外，由于可能生成非常大的树，会消耗大量的时间和空间，大型数据库结构并不适合此算法［6］。

为解决上述问题，本篇论文在FP-Growth算法的基础上提出了一种改进的频繁模式挖掘算法MGFP-growth。主要改进有两点：1）采用二维矩阵按列存储事务信息，只需要扫描事务数据库一次；2）提出了一种分组构建频繁模式树的结构，可以快速发现频繁模式，同时减少内存消耗。

2 问题陈述

2.1 关联规则

关联规则是X→Y形式的表达式，其中X，Y是项集。它表示项X和项Y之间的关系，关联规则有两个重要的基本度量［7］：支持度（sup）和置信度（c）；支持度（sup）是包含X和Y中所有项的事务百分比，即sup（X→Y）=P（X∪Y），置信度（conf）定义为包含X的事务中也包含Y的部分，即P（Y|X）=P（X∪Y）/P（X）［8～9］。

2.2 频繁项集

频繁的项目集在现实生活数据中很常见，例如在超级商店中一起购买的项目集，频繁出现在交易数据集中的一组项目（例如牛奶和咖啡）就是频繁项集。频繁项集的定义如下：

令I=｛I1，I2，I3，…，In｝为项目的集合。D是数据库中的一组事务，其中每个事务T是一组项，因此I包含T。对于包含在I中的任何事务A，当且仅A⊆T时，A才能称为项目集。项目集A的支持计数是数据库D中包含A的事务的数目。如果项目集A的支持计数大于或等于给定的最小支持度minsup，则A可以称为频繁项目集［10～11］。

2.3 FP-growth算法

FP-growth算法在不产生候选项的情况下挖掘出完整的频繁项集，它将表示频繁项的数据库压缩到频繁模式树中来保留项之间的关联。当挖掘所有频繁项集时，只需要两次数据集扫描［12］。第一次扫描统计每个项的出现次数，第二次扫描构造包含原始数据集所有频繁信息的初始FP树［13］。挖掘数据集就变成了挖掘FP树，FP-gowth算法的挖掘过程如下所示［14～16］。

输入：事务数据库，最小支持度minsup

输出：频繁模式集

方法：

Step1：扫描事务数据库，得到频繁向的集合和每个项的支持度计数，并按其支持度降序排序，记为L。

Step2：把数据库中的每个事务的频繁项按照L的顺序重排。并按照重排之后的顺序把每个事务的每个频繁项插入以null为根的FP-tree中。如果插入时频繁项节点已经存在了，则把该频繁项节点支持度加1；如果该节点不存在，则创建支持度为1的节点，并把该节点链接到项头表中。

Step3：调用FP-growth（Tree，null）开始挖掘。伪代码如下：

为了得到的数据更加完整和准确，本研究确立了多个统计对象：浙江省农业厅休闲观光协会处得到的“各地区农庆节庆活动调查”资料；百度首页搜索的结果，输入“城市名”+“果名”+节，如“杭州蜜梨节”，“浙江省“2012’四季鲜果采摘游系列活动”中以时鲜水果采摘游的形式串成一线的35个优秀农庆节庆活动；“最具影响力农庆名单”中与果树观光采摘相关的节庆；“浙江省优秀农庆节庆名单”中与果树观光采摘相关的节庆。

procedure FP_growth（Tree，α）

ifTree含单个路径Pthen｛

for路径P中结点的每个组合（β）

为了更好地说明FP-growth算法的详细过程，举例如表1所示。

表1 样本数据

使用表1中的样本数据生成FP-tree，如图1所示，设置最小支持度阈值minsup=3。

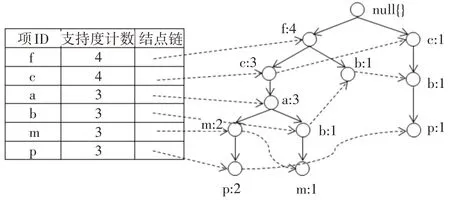
图1 存放压缩的频繁模式信息的FP树

通过FP-growth算法对图1中的FP-tree进行挖掘，得到如表2所示频繁模式集。

表2 通过创建条件（子）模式基挖掘FP树

3 改进算法

3.1 改进算法思想

为了提高FP-growth算法的挖掘效率，从缩减扫描事务数据库的次数以及优化FP-tree的结构方向改进。首先，弃用项目表头，用二维矩阵存储项集的信息。由于项目头表需要扫描一次数据库才能生成，所以减少了一次遍历数据库的次数。其次，对FP-tree构造进行扩展，提出了一种新的树结构MGFP-tree（matrix and group frequent pat⁃tern-tree）。由于在生成FP-tree过程中没有充分利用原事务中频繁项之间的关联关系，因此降低了频繁模式的挖掘效率。在新构造的MGFP-tree中，利用存储在数组中的分组节点，可以快速构建频繁模式树并发现原事务中的频繁项集。

3.2 矩阵

扫描事务数据库D并将其映射成矩阵Dmxn，其中M表示的项数，N表示的是事务数加1。Dmxn中的第一列表示的是事务中不同的项Ii（i<=M），每一行表示的是每个项Ii在每一条事务Tj（j<=N）中对应的值，如果存在值标记为1，否则标记为0。设置辅助一维数组count，记录每个项Ii的个数，同时根据数组count存储的值删除不满足最小支持度阈值的行。最后，为方便后续MGFP-tree的生成，根据count中对应每个项的不同支持度进行降序排序。

为了更好的说明二维矩阵的存储方式，使用表1中给的样本数据进行说明。其中表3中第一列表示的是项集，最后一列表示的是存放在数组count中的每个项的支持度计数。

表3 存放事务的二维矩阵和项支持度计数的数组

3.3 分组

根据上述生成的矩阵，按列垂直向下扫描，如果边界值matrix［j］［i］和martix［j-1］［i］为“0，1”、“1，1”、“1，0”的情况，将其分组存到ArrayList（group表示自定义的类）中并为每个group设置name，colname，end，parenttrace，parent，lastparent属性。其中end表示每个group结束的下标位置，方便树的快速建立。parent表示同一列不同group的父亲节点，如果无则为空。parenttrace属性表示每个group的路径信息，若group1和group2的name、parenttrace相 同，将group1的count加1、group2的count置为0、valid置为0，可以进一步地缩小建立频繁模式树的内存空间和时间。

根据表4可以得到如下分组。

表4 按minsup排序后的二维矩阵和数组

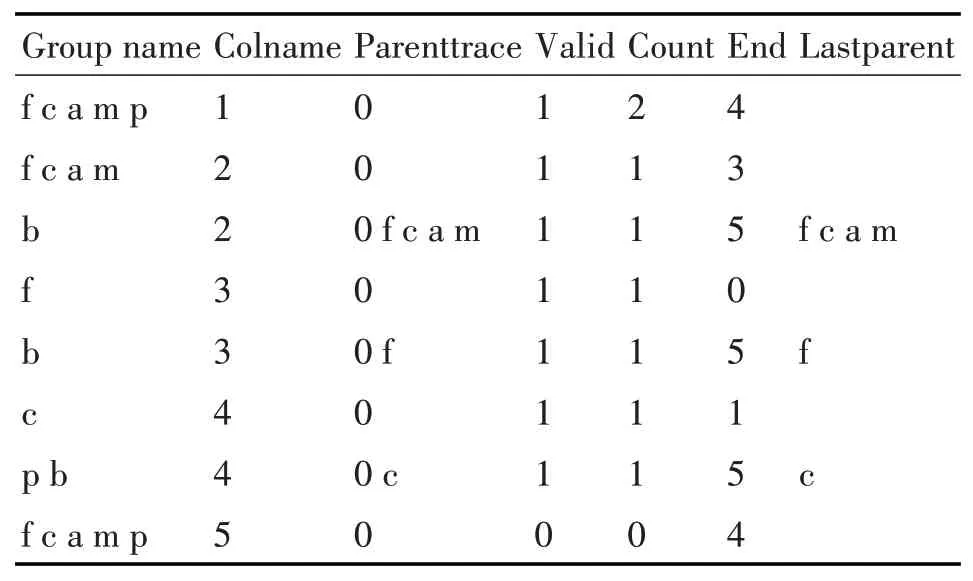
表5 分组后的group对象

3.4 构建MGFP-tree

通过分组已经建立了各个group的关系，类似于一个树的层次关系存储在数组中。首先按照group中end的值的大小从数组中取值，如果valid是有效地将其赋值给封装好的ItemsetTree对象并建立辅助根节点root，最后通过二叉树的后序遍历以及parenttrace和parrent属性依次向二叉树中插入节点。如图2所示。

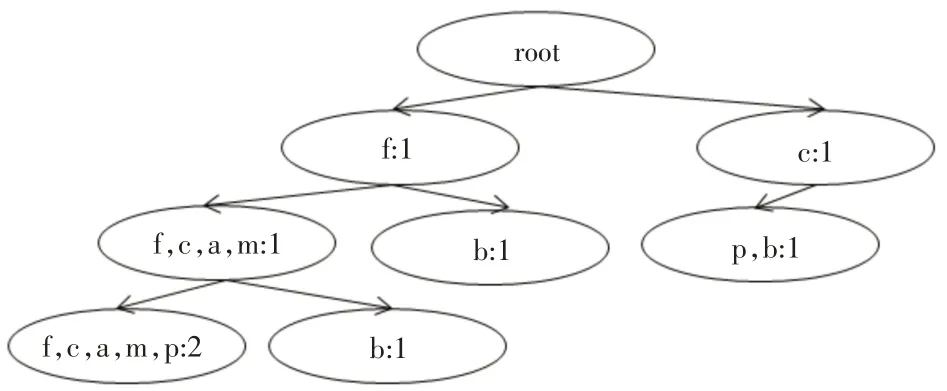
图2 存放分组节点的MGFP-tree

3.5 MGFP-growth挖掘

通过后续遍历统计各个节点的孩子个数count，并将count值赋值给tempcount，tempcount用来保存新的节点计数。因为叶子节点没有孩子节点，所以能够很快的得到左孩子和父节点的关系，如果左孩子节点的nodename包含父节点的node⁃name，则父节点的tempcount更新为左孩子节点的tempcount加父亲节点的tempcount。将右子树上的不同于父节点的项添加到父节点的nodesplit中，用来跟左子树的nodesplit进行对比，如果遍历过程中包含相同的项，则将其nodesplit的nodesplitcount值加1。最后，将每个节点项nodesplitcount值和最小支持度比较，如果满足则和父节点组合，产生频繁项集。

为了更好地说明改进后算法的挖掘过程，根据图2中的MGFP-tree详细说明：首先通过后续遍历，得到节点“f，c，a，m，p”，判断其有没有孩子节点，如果没有遍历下一个节点“b”，因为节点“f，c，a，m，p”和“b”都没有孩子节点，所以遍历“f，c，a，m”，从图中可以看出节点“f，c，a，m”和“f，c，a，m，p”存在父子关系，而且子节点的nodename包含父节点的nodename，所以“f，c，a，m”的tempcount加1，依次遍历得到满足最小支持度阈值的有：“f，c，a，m：3”，“f：4”。其次，将非叶子节点添加到其父节点的nodesplit中，比如节点“f”的nodesplit为“f，b”，然后循环遍历左子树上左孩子就可以得到每个节点的nodesplitcount值，比如“b”在“f，c，a，m，b”中出现了一次，故将其nodesplitcount值加1；得到节点“f”的nodesplit为（b，f），nodesplitcount为（2，4）。最后将满足最小支持度阈值的节点和其父节点组合得到频繁模式。

4 算法性能验证及结果分析

为验证改进算法MGFP-growth的有效性，将MGFP-growth算法、FP-growth算法在相同的实验环境下进行两组不同的实验比较。文中算法的实验平台为：Intel Core i5-3210M CPU 2.5 GHz处理器和4 GB内存，Windows 7 64操作系统，开发平台为MyEclipse 2015。实验所采用两组数据集。一组数据集为mushroom，该数据集事务总数为8124条，项的个数为19个，每个事务的平均长度和最大长度为23；另外一组数据集为T10I4D100K，该数据集事务总数为100000条，项的个数为870个，每个事务的平均长度和最大长度为分别为29、10。下载地址为：http：//fimi.uantwerpen.be/data。

两组实验是通过改变最小支持度阈值来计算算法运行时间，实验对比如图3、4所示。

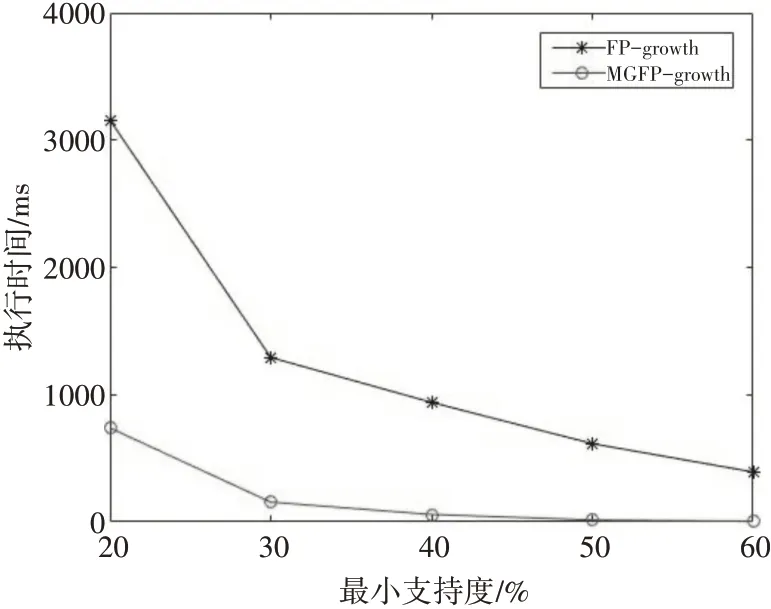
图3 mushroom数据集上的运行时间

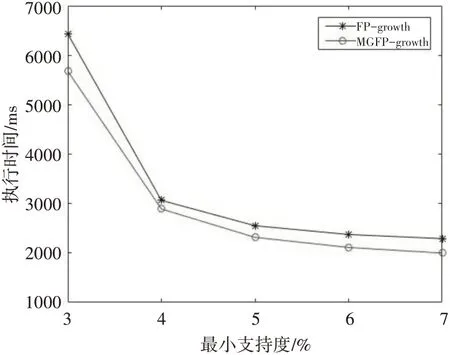
图4 T10I4D100K数据集上的运行时间

从上面实验结果可以看出，随着最小支持度的增加，两种算法的运行时间都在减小，但MG⁃FP-growth效率更高。mushroom该数据集相对稠密，说明必然存在非常庞大的频繁项集，而MG⁃FP-growth算法将每组事务中的频繁项集进行分组，减少了树的分支，可以更快地发现频繁模式，所以运行更快。T10I4D100K该数据集相对稀疏，而且每条事务之间长度差异较大，说明其频繁项集相对于项结点来说较少，所以两者基本一致，但MG⁃FP-tree利用矩阵存储事务信息，只需要扫描事务数据库一次，所以效果更好一些。

5 结语

本篇论文针对传统的关联规则算法存在的固有缺陷，提出了一种基于FP-growth算法的频繁模式挖掘算法。首先，利用矩阵对事务存储，不需要创建项目头表，减少了事务数据库的扫描时间。其次，对FP-tree数进行改进，提出了一种新的树形结构MGFP-tree，新的树结构，可以充分利用每条事务中的频繁项集，同时不需要递归产生大量的FP-tree，减少了内存消耗。最后，通过实验设置两组不同的实验验证了改进后的算法执行效率优于传统算法。