对不连续帕累托前沿的一种改进的MOEA/D*

张宁 高尚

（江苏科技大学计算机学院 镇江 212003）

1 引言

随着Schaffer［1］提出了第一个多目标进化算法（MOEA），越来越多的人将进化算法应用于求解多目标优化问题。传统的MOEA主要是基于帕累托支配的思想，例如文献［2～4］。他们已通过实验与应用验证了对处理多目标优化问题的有效性。但是近年来基于分解的MOEAs越来越被人们关注，例如文献［5～9］。

Zhang和Li最先提出了基于分解的多目标进化算法的框架［5］。相比于基于帕累托最优的方法，大多情况下MOEA/D可以得到更好的帕累托近似前沿，并且其效率也已被证实。自此之后，越来越多的学者对MOEA/D展开了深入的研究：Li和Zhang将差分进化操作应用于MOEA/D［10］；Ke Li提出了一种结合支配与分解的MOEA，通过结合支配和分解的优点以平衡进化的收敛性与多样性［11］；Xiaoyu He等提出一种基于动态分解的MOEA，使用解本身作为权向量而不是使用预定义的权向量［12］。

虽然MOEA/D对于简单帕累托前沿的MOP有着非常好的表现，但是对于复杂帕累托前沿的问题，并不能得到一个很好的近似解集。尤其是对于不连续的帕累托前沿问题，MOEA/D得到的近似帕累托前沿，几乎都会出现近似帕累托前沿分布不均匀以及无法覆盖完整帕累托前沿的问题。

本文提出了一种改进的MOEA/D解决这些问题。核心思想是使用基于密度的聚类算法判断是否为不连续帕累托前沿的优化问题。如果是，则将其转化为数个连续帕累托前沿的优化问题并协同演化。通过权向量重生成和种群重分配解决不均匀和不完整的问题。本文将这种算法命名为MOEA/D-DE-DC。

2 相关知识

2.1 多目标优化问题

在现实世界中存在着许多多目标优化问题（MOP），其可以被定义为

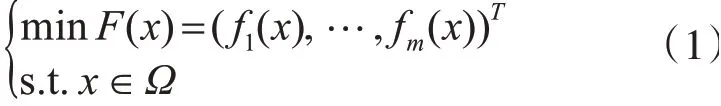
其中x为决策向量，Ω为n维决策空间，F:Ω∈Rm中包含了m个需要同时优化的目标函数，Rm为目标空间。

2.2 MOEA/D

MOEA/D的主要思想是将一个多目标问题通过聚合函数分解为若干个单目标问题，然后同时优化所有的单目标问题。Zhang和Li提出了三种聚合函数：惩罚边界交叉、加权和以及切比雪夫［5］。在本文中，为了简单我们选择使用切比雪夫分解方法，公式如下：

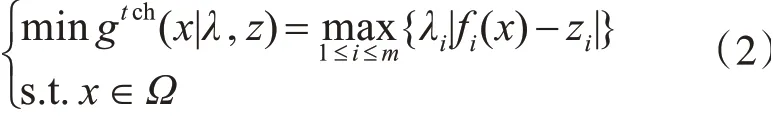
其中λ为权向量，z为参考点。每一个权向量所对应的子问题的最优解就是MOP问题的帕累托最优解，所以可以将所有子问题最优解的集合看作PF的良好近似。

2.3 DBSCAN

DBSCAN是一种经典的基于密度的聚类算法［13］。它具有无需预先设定聚类的数量，可以识别任意形状的簇等优点。本文中的算法需要在第一阶段结束时对得到的近似PF进行聚类，通过聚类的数量判断是否属于不连续PF的问题，所以将DBSCAN引入其中。DBSCAN需要的输入的参数为邻域半径ε和正整数MinPts。

3 MOEA/D-DE-DC

3.1 算法的总体框架

算法1为MOEA/D-DE-DC的总体框架。由于我们不知道一个MOP问题的PF是否为不连续的，所以整个算法分为两个阶段。第一阶段使用正常的MOEA/D-DE算法，获得PS和近似PF。第二阶段，通过DBSCAN判断PF是否为不连续的，如果是不连续的，则将种群按聚类划分，将其转化为数个连续的PF的子问题并协同演化，最后输出近似PF。如果是连续的PF则仍然使用第一阶段的算法完成演化。

3.2 参考点集的设置

在算法1中步骤8需要为每一个类设置参考点。我们定义这一组参考点为参考点集Z，公式如下：

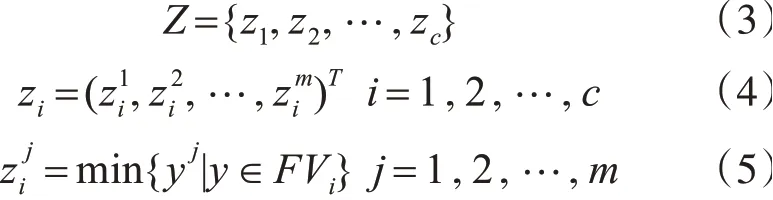
其中c为通过聚类算法得到的类别数。为了方便后面内容的描述，这里还给出反置参考点集R的定义：

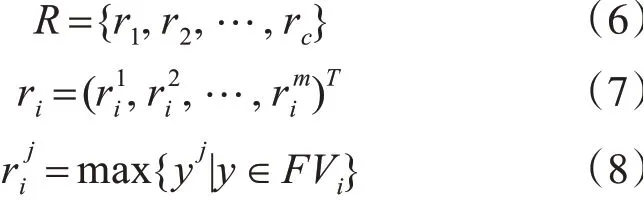
3.3 权向量的重生成和种群的重分配

由于将整个种群划分为C个子种群，如果C大于1，在第一阶段中生成的权向量已经不适用于第二阶段了，需要为每一个子种群生成一组新的权向量。而每一个子种群的权向量的个数决定了最终解集的分布。为了解决在第一阶段结束帕累托解集分布不均匀的现象，需要通过每一子类种群中目标向量分布空间的大小占总分布空间的比重来衡量其需要生成的权向量的数目，公式如下：

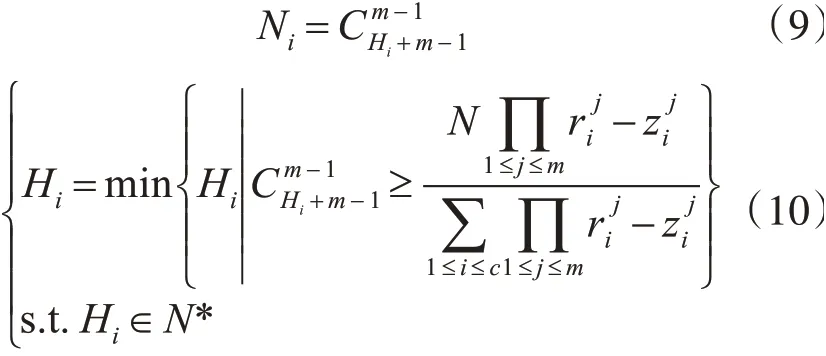
其中Ni为第i个子种群生成权向量的数量，对于每一个子种群的权向量的分解方法仍然使用的是Das和Dennis的方法［14］。第i组权向量的邻居数量设置为：

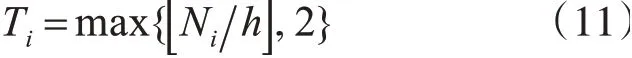
然后将种群重新分配给新生成的数组权向量。不重新生成新的种群，是为了最大程度的利用第一阶段的计算资源，加快优化速度。种群重分配的过程如算法3中所示：

这种算法的好处在于可以最大程度地保存种群的多样性，同时又不会使得某个个体重复的次数过多。在分配个体的时候引入贪心策略，因为种群重分配不需要达到最优，在第二阶段的进化中算法可以自行调整。

3.4 种群更新

种群更新的详细过程如下：

算法3种群更新

输入：经过聚类的种群x；

经过聚类的近似帕累托前沿FV。

输出：经过聚类的种群x；

经过聚类的近似帕累托前沿FV。

步骤1 Fori=1，2，…，c，j=1，2，…，NiDo：

步骤1.1选取父代个体：生成一个随机数u∈[0，1]，然后通过公式4.1设置Q；

步骤1.2生成子代：从Q中随机选择两个索引k与l，将xi、xk和xl使用差分进化算子产生子代个体x′，在通过多项式变异产生x″；

步骤1.3调整：若x″不在邻域目标可行域中，则重新生成x″；否则计算其所属子类种群的索引b；

步骤1.4更新参考点zb：对每一个a=1，2，…，m，如果，则将

步骤1.5计算评价函数F(x″)

步骤1.6更新种群：设置o=0，然后：1）如 果o=nr或Q=∅ ，则 转 至 步 骤1，否 则 从M={(b，1)，(b，2)，…，(b，Nb)}中随机选择一个索引（b，d）；

3）将（b，d）从M中删除，o=o+1，转至1）。

步骤2输出x和FV。

步骤1.1Q的计算公式如下：

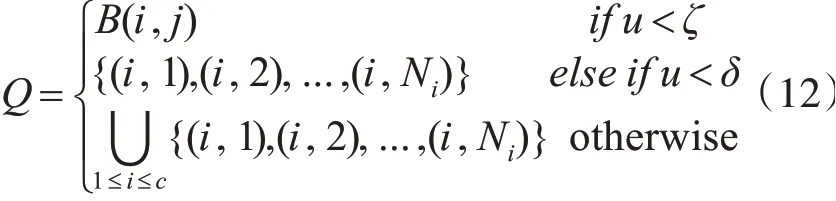
其中u为随机数，取值范围为[0，1]；δ，ζ为控制参数，0<ζ<δ<1。

步骤1.3中需要计算邻域可行目标域。对于i=1，2，…，c，定于第i个子类种群的邻域目标可行域SPi为

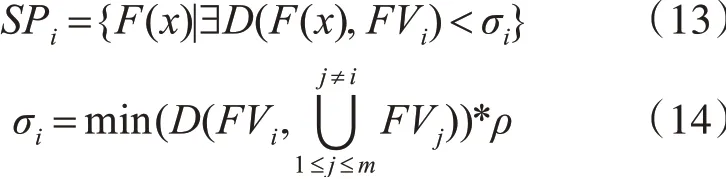
其中ρ表示收缩因子，是控制σi大小的参数，取值范围为(0，0.5)。

4 实验结果与分析

4.1 测试函数与对比算法

为了验证本改进算法的性能。选取了广泛使用的测试测试函数ZDT，DTLZ，WFG和MOP。其中ZDT1和ZDT2的PF为连续的；其他测试函数的PF均为不连续。MOP4为三目标测试函数，其余测试函数为两目标。所有测试函数的决策域均为30维。使用MOEA/D-DE与其改进的算法MOEA/D-DE-DC进行对比。

4.2 参数设置

本次实验使用Matlab2019平台。操作系统为Win7。为了相对公平，两算法相同的参数都设为相同的值。所有算法的参数设置如下：

1）DBSCAN的参数设置：MinPts=2，WFG2中ε=0.3，MOP4中ε=0.2，其余ε=0.1。

2）DE算子：CR=1.0，F=0.5。多项式变异算子：η=20，pm=1/n。

3）每个测试函数独立运行20次。算法在达到最大迭代次数600次后停止运行。

4）两目标的种群规模为100，三目标的种群规模为300。

5）其他控制参数：Mr=0.75，h=4，ζ=0.3，δ=0.9，T=N/10，nr=2。两目标问题ρ设为0.35，三目标ρ设为0.3。

4.3 评价指标

本文采用多目标进化算法中最广泛使用的评价指标，即IGD（Inverted Generational Distance）［15］。IGD可以提供有关所得解集的多样性与收敛性的可靠信息。设PF为从真实POF均匀采样的一组解，PF*为目标空间中的一组近似解，IGD的计算公式如下：

其中d(a，PF*)是a与PF*中所有点的欧几里德距离的最小值。IGD的值越低表示PF*越趋近与真实PF。本次实验中所有测试函数从PF中采样点的数量设置为500。

4.4 性能测试

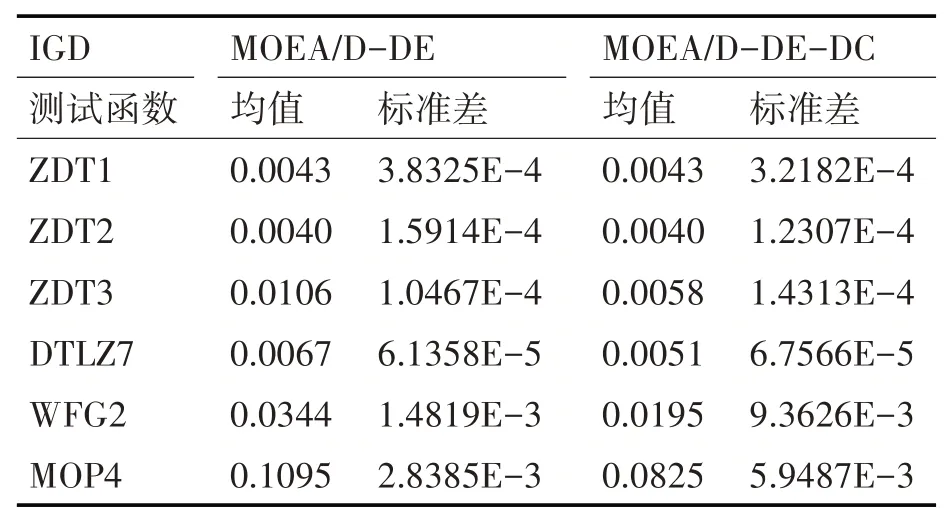
表1 MOEA/D-DE与MOEA/D-DE-DC的IGD

图1 为两个算法种群的平均IGD值随迭代次数变化的折线图。因为两个算法前半部分相同所以只截取了从401～600次迭代的数据。从图中可以看出MOEA/D-DE-DC在不连续的多目标优化问题中在IGD度量方面都表现的更加优秀。其中450次迭代是MOEA/D-DE-DC第一阶段与第二阶段的分界线。可以看到图3～图5在迭代次数450的刻度附近都存在一段尖峰，这是因为种群的重分配一般会对解集的分布产生一定的影响。随后IGD值都快速地收敛到了一个更低的值，说明本算法对处理不连续PF的问题有很大提升。

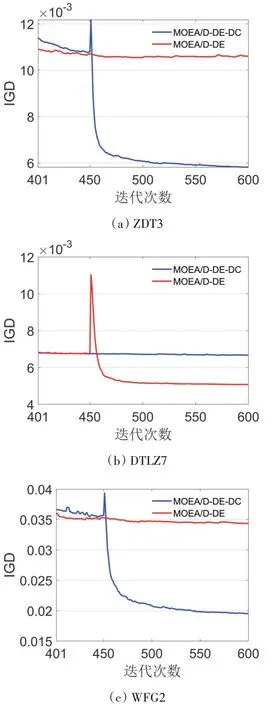
图1 MOEA/D-DE与MOEA/D-DE-DC的IGD收敛曲线

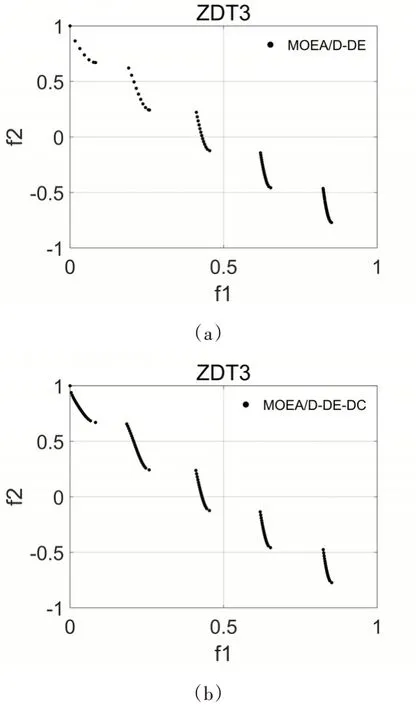
图2 为两个算法在个测试函数上得到的近似PF，所有图均取20次独立测试的第一次测试数据绘制。由图可以明显地看出所有MOEA/D-DE-DC的不连续PF的测试函数获得的近似PF分布明显更加均匀与完整。

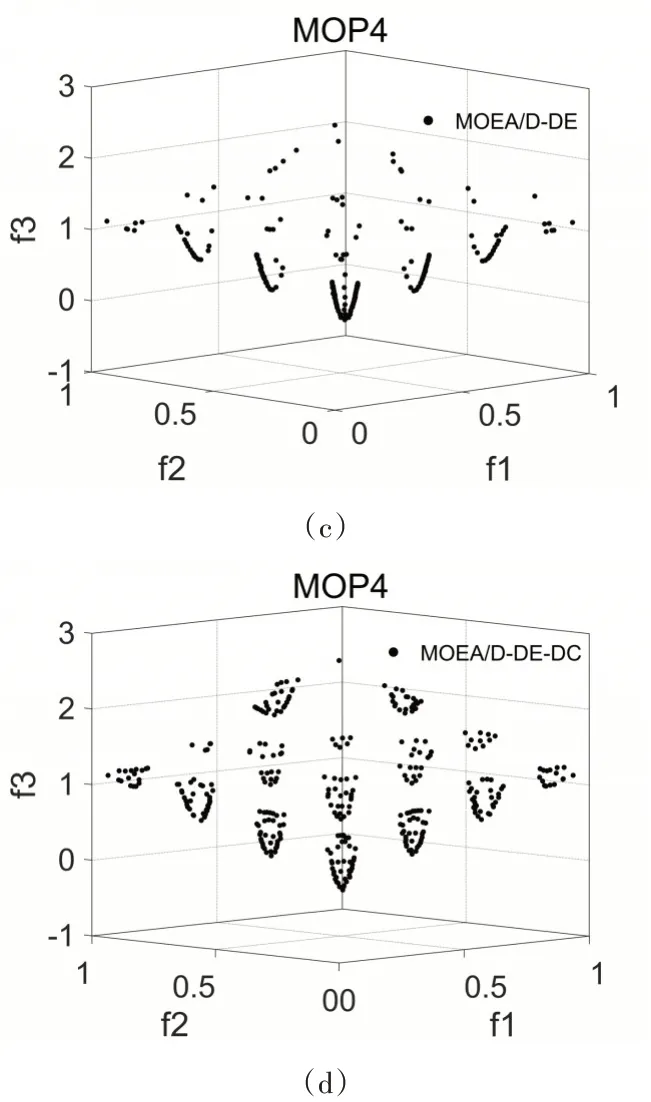
图2 MOEA/D-DE与MOEA/D-DE-DC在测试函数上的近似帕累托前沿分布图

5 结语

本文提出了一种改进的MOEA/D，即MOEA/D-DE-DC。其可用于解决不连续PF的多目标优化问题中出现的近似PF不均匀与不完整的问题。将其与未改进的MOEA/D-DE进行对比。实验结果表明MOEA/D-DE-DC在不连续PF的优化问题中性能有着显著的提升。通过将不连续的PF问题转化为数个连续的PF子问题，可以有效地降低PF形状对算法性能的影响。将来，我们计划研究MOEA/D解决更多目标以及更复杂PF的MOP的能力。