基于改进双耦合Duffing振子的微弱信号检测方法

李景贵，靳伍银

(兰州理工大学机电工程学院，甘肃兰州 730050)

0 引言

传统的微弱信号检测方法主要有相关检测方法、电子学检测方法、高阶统计量法、自适应噪声抵消法等[1]，这些方法主要从噪声的角度分析信号的特点和噪声的规律，通过噪声和信号的不同提取出微弱信号，但所检测的最低信噪比有限。而以混沌理论为核心的非线性科学的发展为微弱信号检测提供了新的思路[2-4]。自1992年Birx等提出运用混沌振子对微弱信号检测以来，混沌振子检测微弱信号得到了不断的改进和发展。王梦蛟等基于受控Chen’s系统，实现了淹没在强噪声背景中的微弱谐波信号检测[5]。赖志慧等分析了级联双稳Duffing系统的随机共振特性，证明了级联双稳Duffing系统有更好的随机共振输出，可以实现含噪方波信号的恢复[6]。王晓东等利用Duffing振子和Van der Pol振子耦合，提出一种Duffing振子阻尼力耦合方法[7]。李国正等结合遗传算法求解系统输出方差的极值得到待测信号频率[8]。黄继尧等的研究实现了提取未知多频率微弱信号各信号分量的频率参数[9]。行鸿彦等结合互补集总经验模态分解方法和变尺度Duffing振子，提出了一种新的微弱信号检测方法[10]。但是混沌理论的大部分研究处于实验仿真阶段，提高检测系统对噪声的免疫力还有待进一步研究[11-12]。

本文通过改变常规Duffing振子的非线性项和耦合系数，提出了一种新的混沌振子检测模型，研究了基于改进型双耦合Duffing振子系统的微弱信号检测方法。利用双耦合Duffing混沌振子对微弱信号的敏感性和对强噪声信号的免疫力，以及2个振子之间相互控制的过程，提高系统临界阈值的准确性，为微弱信号检测提供一种新的途径。通过对双耦合Duffing振子系统的建模、动力学分析以及微弱信号检测研究，同时结合EEMD分解方法对待测信号分解，仿真结果表明在检测淹没在强噪声背景下的微弱信号时可以避免相位变化不稳定问题，解决了检测多周期分量的含噪声微弱信号时出现的混频问题。 最后对建立的模型和提出的方法进行了仿真实验和比较。

1 集合经验模态分解(EEMD)方法

研究表明虽然Duffing系统对噪声具有良好的免疫性，但是只有在噪声功率比较低的情况下检测微弱信号才有较好的效果，并且检测范围受到信噪比门限的限制，因此利用Duffing系统检测强噪声背景下的微弱信号时性能比较差。同时Duffing系统仅能检测单一同频的周期信号，而实际工程信号通常含有多个周期成分[13-14]，将含噪声信号输入Duffing系统前，对信号进行EEMD分解处理，将含噪声信号分成多个周期的IMF分量，再经过Duffing系统将其检测出来。研究发现EEMD分解可以规避模态混叠问题。

1.1 EEMD分解的原理

EEMD方法是对EMD方法的改进，解决了EMD方法模态混叠和误差大问题。在EEMD分解中，由于辅助白噪声和集合平均次数是影响EEMD分解的2个重要参数，则对添加白噪声方法改进得到新的EEMD方法，其主要思路是：在s(t)中加入绝对值相等的正负2组白噪声+k·σx·n(t)和-k·σx·n(t)构成如下信噪混合体S1(t)和S2(t)，其表达式分别为：

S1(t)=s(t)+k·σx·n(t)

(1)

S2(t)=s(t)-k·σx·n(t)

(2)

式中：n(t)为归一化白噪声；σx为信号标准差；k为比例系数；s(t)为待测信号。

将S1(t)和S2(t)进行EMD分解成IMF组合，并每次加入不同的白噪声得到：

(3)

(4)

式中：S1,i(t)和S2,i(t)为加不同白噪声后经EMD分解后的信号组合；c1,i,j和c2,i,j为加入不同白噪声后经EMD分解的IMF分量；r1,i,m和r2,i,m为分解后的残余分量。

对式(3)和式(4)进行N次迭代后，各IMF和残余分量的平均值为

(5)

式中：cj为IMF分量平均值

(6)

式中：rm为残余分量平均值。

最后分解结果为

(7)

由于白噪声的零均值特性，将这些多次分解的结果取平均值后，噪声最终被最大限度的抵消而达到消除的效果，总体平均值可以作为真实信号。

1.2 EEMD与EMD方法检测性能的对比分析

EMD分解是建立在傅里叶变换之上，由于其高效自适应分解非线性、非平稳信号的能力，EMD降噪方法得到广泛的应用。但是，由于EMD分解存在模态混叠和误差较大等问题，严重影响检测结果的准确性，因此本文利用其改进型EEMD方法进行弱信号检测，通过仿真实验将EEMD与EMD方法检测性能进行对比分析。取待测信号如下

s(t)=sin(0.2πt)+0.5sin(0.4πt)+0.15sin(0.8πt)+sin(πt)+n(t)

(8)

对待测信号s(t)进行EMD分解如图1(a)所示，其中第一个信号Signal为待测信号s(t)时域图；对待测信号s(t)进行EEMD分解，如图1(b)所示。由图1(a)可以发现，第二个低频正弦分量IMF2受到IMF1影响，在IMF2分量中出现IMF1分量，2个IMF分量出现模态混频现象，IMF1和IMF2不能代表相应的检测信号分量，凸显EMD分解方法的不足。

图1(b)中，EEMD分解方法克服了EMD分解方法的不足，将含噪声的s(t)的4个分量成功分解出来，保持了原信号的真实性，为之后的Duffing振子微弱信号检测做好降噪和信号分解准备。

2 Duffing振子检测原理

由于Duffing系统具有复杂的动力学特征，如振荡、同宿轨道、分岔、混沌等，本文利用Duffing振子中非线性恢复力对振子动力学特性的影响，改变常规Duffing振子的非线性恢复力项的次数构造出改进的方程，其数学模型如下

(9)

式中：k为阻尼系数；ax3+bx7为非线性恢复力,a和b为非线性恢复力系数；fcos(wt+θ)为周期策动力，f为周期策动力幅值，w为周期策动力频率，θ为初始相位。

(a)EMD分解结果

(b)EEMD分解结果图1 EEMD与EMD分解结果对比

(10)

对改进的Duffing振子进行动力学分析，取k=0.5，a=1，b=1，w=1，θ=0，f是可变参数，随着它的取值从小到大的变化，系统经历不同的状态。当f=0，系统的相平面鞍点为(0，0)，焦点为(1，0)和(-1，0)，相轨迹最后停在两焦点之一。当f≠0，由于策动力的扰动，系统具有了复杂的运动状态，通过数值计算和仿真结果表明，当f取不同的数值，Duffing系统出现周期振荡、同宿轨道、倍周期分岔、混沌状态、临界状态和大尺度周期状态。由Melnikov函数可计算出系统由混沌状态变为大尺度周期状态的临界阈值为fd，当f逐渐增大接近阈值fd时，系统临近大尺度周期状态，ffd时，系统立刻由混沌状态进入大尺度周期状态，相轨迹如图3所示。

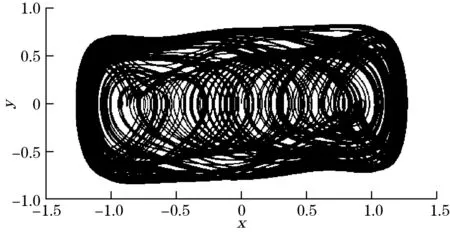
图2 混沌状态相轨迹

图3 大尺度周期状态相轨迹

当向Duffing系统中加入外界扰动项时，混沌检测系统为

(11)

式中：s(t)为待测信号s(t)=rcos(w1t)+n(t)；n(t)为高斯白噪声。

设定系统参数f≤fd，此时系统刚好处于临界阈值状态，当加入与系统周期策动力同频率同相位的微弱周期信号时，系统总周期策动力幅值fd+r将大于阈值fd，系统将转化为大尺度周期状态，从而检测出微弱信号。当待测信号不存在与系统同频同相的信号时，系统依然为混沌状态。从而，通过判断系统是否转化为大尺度周期状态就可以判断待测信号中是否存在微弱周期信号。

3 双耦合Duffing振子

3.1 模型构建

单Duffing振子在检测淹没在强噪声背景下的微弱信号时，常会发生相轨迹变化不稳定、噪声影响检测结果等问题，导致过小的信号不能准确的检测出来。为了避免单Duffing振子的不足，本文提出了一种改进型双耦合Duffing振子检测模型来提高检测含噪声微弱信号的准确性。

对Duffing混沌振子检测系统(11)采用阻尼项进行耦合，建立如下的数学模型

(12)

式中：ax3-bx7与au3+bu7为非线性恢复力，a和b为非线性恢复力系数,通常取值为1；c(x-u)与c(u-x)为耦合振子的线性耦合项，c为耦合系数；fcos(wt)为周期策动力；s(t)=rcos(w1t)+n(t)为待测信号,n(t)为噪声信号。

实际工程信号检测中，要将某一频率成分的信号检测出来，就要将策动力频率w设置为待测信号的频率w1，但待测信号频率w1值往往很难确定。为了满足工程需要和减少计算量，对时间t进行尺度变换，假设t=wτ，则有

(13)

(14)

同理有

(15)

代入方程(12)整理得

(16)

此时，方程(16)的检测特性和方程(12)是一致的，但是系统的策动力频率由1 rad/s扩展到wrad/s，适应了外界不同频率的周期信号，实现双耦合Duffing系统自适应对工程中不同频率微弱信号的检测。

3.2 模型分析

双耦合Duffing振子系统中的耦合系数c值越大，说明系统的耦合度越高，不同振子间的同步性越强。当c=0时，双振子间的耦合作用消失，双Duffing振子系统的动力学行为与单Duffing振子系统的完全相同。当c≠0时，系统的变量将在耦合作用的影响下随时间逐步达到同步。为进一步说明耦合系数对双耦合Duffing振子系统抗噪性及稳定性的影响，研究中引入标准差概念(如式(17))来计算不同噪声背景下的不同条件下的标准差，如表1所示。

(17)

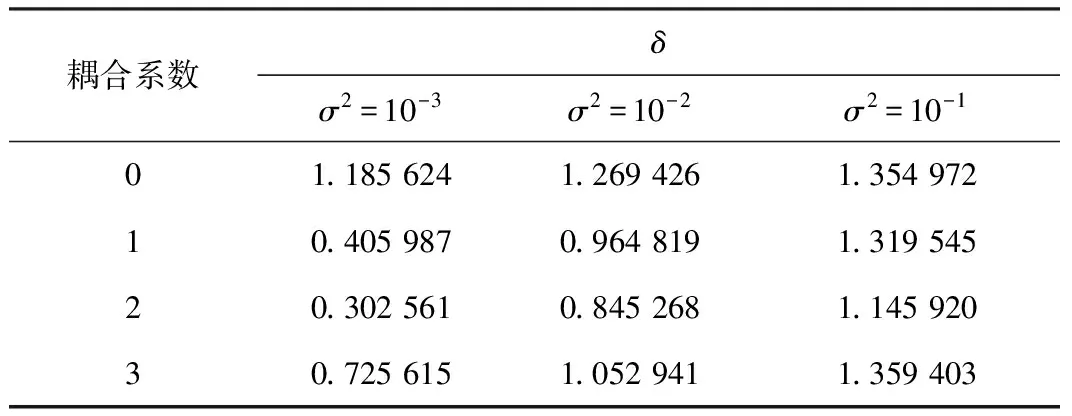
表1 双耦合Duffing振子系统在不同噪声 下不同c对应的标准差δ

由表1可知，随着噪声强度σ2的增大，不同耦合系数c下的系统标准差δ也逐渐变大，则表明对于双耦合Duffing振子系统，标准差越小，系统的稳定性越强。从表1研究中可知，在耦合系数(c=2)时双耦合检测系统的性能最优。

3.3 仿真实验研究

为验证结合EEMD方法的双耦合Duffing振子系统的检测性能，选择待测信号s(t)为

s(t)=0.000 1cos(5t+0.1π)+0.000 3 cos(40t+0.2π)+

0.000 6 cos(100t+1.5π)+n(t)

(18)

由于实际工程中信号的复杂性，因此在输入信号s(t)中加入功率为0.1的高斯白噪声。对混合多频信号s(t)进行EEMD分解后得到8个固有模态函数，除去噪声分量和残余分量得到3个具有实际意义的IMF分量，如图4所示。从图4中看出，IMF1～IMF3分别是从高频到低频排列的3个正弦信号。经EEMD分解后，混合信号s(t)分解为尺度不同的信号，虽然EEMD分解规避了模态混叠和去除了一定的噪声，但是从图中发现IMF分量中仍含有混杂噪声，分解信号IMF1～IMF3的信号参数很难确定，则将IMF1～IMF3分别输入到Duffing振子检测系统中，通过混沌检测方法检测出各IMF分量参数。

图4 EEMD分解的信号

设置式(12)中的双耦合Duffing系统参数，阻尼比k=0.5，初始条件为x(0)=u(0)=0,f=0.677,高斯白噪声功率为0.1，使用四阶Runge-Kutta法进行求解，将IMF1～IMF3分别作为外部激励信号输入到双耦合Duffing振子系统中，得到如图5所示的相轨迹图。

(a)IMF1输入系统后相轨迹图

(b)IMF2输入系统后相轨迹图

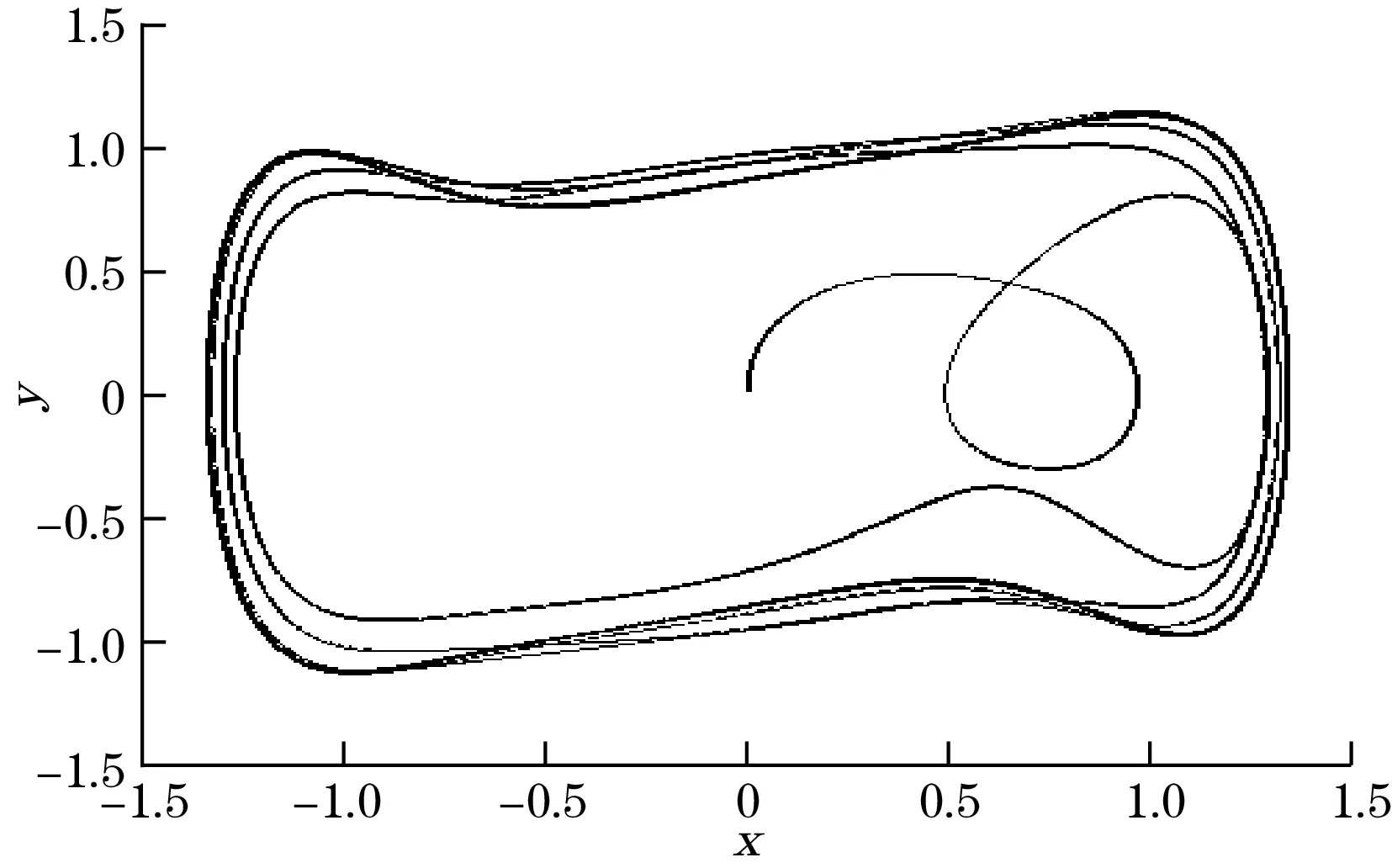
(c)IMF3输入系统后相轨迹图图5 各IMF分量分别输入系统后的相轨迹图

由图5可知，分别输入IMF1～IMF3后双耦合系统发生了转变，证明了微弱周期信号的存在。由Melnikov函数可计算出输入IMF1～IMF3后分别对应的临界阈值fd为0.676 4、0.676 7、0.676 9，而不加入待测信号时的临界阈值fd=0.677，从而根据Duffing系统的检测原理可知待测信号的幅值为阈值之差，计算得到IMF1幅值为0.006，IMF2幅值为0.000 3，IMF3幅值为0.000 1。仿真实验表明，检测结果和实际的输入信号一致，验证了结合EEMD分解和改进双耦合Duffing振子微弱信号检测方法的可行性及系统的抗噪性。

4 结论

本文提出了一种将EEMD和变尺度双耦合Duffing振子结合的微弱信号检测方法。利用EEMD将淹没在噪声背景下的多周期待测信号分解为多个不同的固有模态函数,通过时间尺度变换和耦合同步构建了双耦合Duffing振子，实现了对复杂未知频率信号的检测。结果表明，该方法检测微弱信号时抗噪性强、检测灵敏，克服了常规Duffing振子仅能检测低噪声背景信号的缺点，对实现实际工程中的微弱信号检测提供新的方法。