梯形悬臂梁压电振动俘能器的特性研究

马天兵，贾世盛，丁永静，尹梦涵

(1.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，安徽淮南 232001; 2.安徽理工大学机械工程学院，安徽淮南 232001)

0 引言

随着无线传感器节点技术的不断发展，无线传感网络已在环境监测和物联网等领域显现出实际应用价值[1-2]。目前，大多数无线传感网络以传统化学电池为其供电，但化学电池不仅存在容量有限、恶劣环境下难以更换等缺点，而且体积较大，限制无线传感网络的微型化和集成化[3]。为了解决无线传感网络长期稳定供电的难题，国内外专家学者致力于环境能量俘获技术的研究[4-5]。

由于振动能在自然环境中无处不在，并具有较高的能量密度，所以常作为环境能量俘获技术的能量源。根据转换机理的不同，振动俘能器可以分为压电式[6]、电磁式[7]和静电式[8]。压电式振动俘能器有较高的能量密度、不受电磁干扰、结构简单以及易于微型化等优点，得到了广泛的关注和应用[9-10]。

易志然[11]等设计了一种阶梯梁压电振动俘能器结构，实验研究结果表明：梁根部加强有助于压电材料利用率的提高以及发电功率的增加。王海[12]等设计了一种多质量块宽频压电能量收集器，实验研究结果表明：随着质量块数量的增加，压电悬臂梁的一阶固有频率降低、频宽增大和输出功率增加。但多质量块结构缺点是对激励响应的敏感程度不如单质量块结构，而且多质量块结构体积较大，不利于压电能量收集器的微型化。Y. Yang[13]等为了提高压电振动俘能器的采集效率，提出了一种圆形薄片状结构，基于应力分布等值线的环形分布，使得压电片的利用率较高，进一步提高了采集性能。陆颢瓒[14]等提出一种固支梁压电俘能器机构，研究结果表明：固支梁组合方案可以实现多谐振频率能量采集。

目前，大部分压电俘能器采用矩形悬臂梁结构，主要由弹性基体、压电材料和质量块组成，这种结构形式也被称为压电振子。压电材料粘贴在弹性基体上，质量块放置在悬臂梁的自由端以降低压电俘能器的共振频率；压电振子是俘能器将环境中的振动能量转换为电能的核心元件，其形状对俘能器的发电能力有较大的影响。本文提出了一种梯形悬臂梁压电俘能器结构，改善了矩形压电振子梁上应变分布不均匀现象，降低了俘能器的固有频率，提高了开路输出电压以及输出功率。

1 结构设计与理论分析

图1为梯形悬臂梁压电振动俘能器的结构示意图，梯形悬臂梁与矩形悬臂梁不同，沿悬臂梁梁长度方向不同处的截面尺寸不同，本文为了简化计算，取压电材料的长度、宽度分别与梁长度、宽度相等，矩形悬臂梁的宽度wa，长度为l；梯形悬臂梁大端宽度与矩形悬臂梁的宽度相同，小段宽度为wb，长度为矩形悬臂梁长度，在沿梯形梁长度方向距矩形梁大端x处取一截面，则该截面宽度wx为

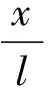
(1)

(a)梯形梁侧视图

(b)梯形梁俯视图

(c)梯形梁截面图图1 梯形悬臂梁示意图

施加在梯形悬臂梁自由端的载荷F，产生一个使悬臂梁弯曲变形沿y轴的弯矩，可得压电振子在长度为x处所受弯矩为[15]

M(x)=F(l-x),0≤x≤l

(2)

(3)

式中：E为弹性基体的弹性模量；I为所取截面对y轴的惯性矩；EI为梁的抗弯刚度；z为该截面任一点沿纵轴的线位移，也是该点的挠度。

由悬臂梁的挠度曲线近似微分方程，得：

(4)

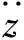
(5)

式(5)中:

(6)

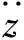
梯形悬臂梁的等效惯性矩为

第三，制度自信是根本保障。根本保障在于坚持和发展中国特色社会主义制度。社会制度实际运行合理与否，并不能简单地将“个体生活”的好坏作为评判标准。西方现代文明的一个根本性缺陷就是简单地将“社会制度”还原为“个体制度”，而彻底地遗忘了社会属性。当代中国是一个有着近14亿人口的大国，中国共产党实现自己的执政理念与执政目标，面对的国际国内环境越来越复杂，肩负的繁重历史使命远超出现代西方选举类型政党。可以说，这个制度是对西方制度的超越。

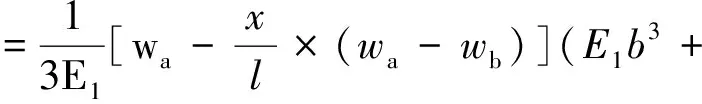
3E2bt2+E2t3)

(7)

假设弹性基体的杨氏模量E1=1.93×1011Pa，压电材料的杨氏模量E2=1.7×109Pa，wa=20 mm，wb=10 mm，l=50 mm，b=0.2 mm，p=0.2 mm，取z=-0.3mm。将式(2)和式(6)代入式(3)可以得到矩形悬臂梁表面应变：

(8)

将式(2)和式(7)代入式(3)可以得到梯形悬臂梁表面应变：

(9)

2 梁的特性分析

采用有限元法对梯形悬臂梁压电俘能器进行力学以及机电耦合特性仿真，其中，弹性基体为黄铜片，质量块选用黄铜块，压电材料是压电陶瓷片，型号是PZT-5H，具体尺寸和参数如表1所示。

表1 梯形悬臂梁具体尺寸与参数

2.1 力学特性分析

分别建立相同面积、相同根部宽度和相同质量块的梯形悬臂梁和矩形悬臂梁的模型，通过comsol软件仿真得到：梯形悬臂梁表面最大应力为13.377 MPa，而矩形悬臂梁面最大应力为13.051 MPa，所以在相同的实验条件下，梯形悬臂梁的压电材料利用率高于矩形悬臂梁。

图2为压电材料不同厚度一阶频率曲线图，从图中可以看出，梯形悬臂梁的一阶固有频率比矩形悬臂梁的一阶固有频率低；在弹性基体的厚度不变的情况下，随着压电材料厚度的增加，梯形悬臂梁和矩形悬臂梁的一阶固有频率也会增加，压电材料厚度对一阶固有频率有较大影响。

图2 压电材料不同厚度一阶频率曲线图

2.2 动力学特性分析

弹性基体的厚度不变，在梯形悬臂梁不接外部负载时，在不同的压电材料厚度下(0.2、0.3、0.4、0.5 mm)，梯形悬臂梁压电俘能器的输出电压-频率曲线如图3所示，梯形悬臂梁压电俘能器的输出功率-频率曲线如图4所示。

图3 不同压电材料厚度的输出电压-频率曲线

图4 不同压电材料厚度的输出功率-频率曲线

从图3可以看出，随着压电材料厚度的增加，梯形悬臂梁压电俘能器的最大输出电压逐渐减小。从图4可以看出，随着压电材料厚度的增加，梯形悬臂梁压电俘能器的最大输出功率逐渐减小。即在弹性基体的厚度不变的情况下，压电材料厚度的变化对梯形悬臂梁压电俘能器的最大输出电压和最大输出功率有较大的影响。

压电材料厚度为0.2 mm时，当外激励加速度幅值发生变化时(0.5g、1.0g、1.5g、2.0g和2.5g)，梯形悬臂梁压电俘能器的输出电压-频率曲线如图5所示。从图5中可以看出，梯形悬臂梁压电俘能器的输出电压随着外激励加速度的幅值增加而增大，且随着外激励加速度的幅值增加，一阶固有频率并没有发生变化。压电材料厚度为0.2 mm，加速度为1.0g时，梯形悬臂梁压电俘能器外接不同负载时(1、2、3、4 kΩ)的功率-频率曲线如图6所示，梯形悬臂梁压电俘能器的最大输出功率随着外界负载的增加而逐渐减小。

图5 不同加速度的输出电压-频率曲线

图6 不同外接负载的输出功率-频率曲线图

梯形悬臂梁压电俘能器与矩形悬臂梁压电俘能器的输出电压对比图如图7所示，外接负载1 kΩ时，梯形悬臂梁压电俘能器与矩形悬臂梁压电俘能器的输出功率对比图如图8所示。

图7 输出电压对比

图8 输出功率对比

从图7可以看出，梯形悬臂梁的最大输出电压是19.73 V，矩形悬臂梁的最大输出电压是11.49 V，梯形悬臂梁的最大输出电压大于矩形悬臂梁的最大输出电压；矩形悬臂梁压电材料和梯形悬臂梁压电材料的表面积和厚度都相同，所以压电材料的表面积为750 mm2、体积为150 mm3，梯形悬臂梁单位体积输出电压是131 V/m3，矩形悬臂梁单位体积输出电压是76 V/m3。

从图8可以看出，梯形悬臂梁的最大输出功率是701 μW，矩形悬臂梁的最大输出功率是390 μW，梯形悬臂梁的最大输出功率大于矩形悬臂梁的最大输出功率；梯形悬臂梁的能量密度是4 673 μW/m3，矩形悬臂梁的能量密度是2 600 μW/m3。所以，从单位体积输出电压及能量密度角度，梯形悬臂梁压电俘能器性能优于矩形悬臂梁压电俘能器。

3 实验研究

通过实验的方式验证理论分析和梁特性分析的正确性。制作出与仿真相同尺寸和材料的梯形悬臂梁并搭建了测试平台，如图9所示。

图9 振动俘能器测试平台

压电材料厚度为0.2 mm时，当外激励加速度幅值发生变化时(0.4g、0.8g、1.0g和1.2g)，梯形悬臂梁压电俘能器的输出电压-频率曲线如图10所示。从图10中可知，当a=0.4g时俘能器最大输出电压为3.36 V，当a=0.8g时俘能器最大输出电压为5.22 V，当a=1.0g时俘能器最大输出电压为8.56 V，当a=1.2g时俘能器最大输出电压为13.8 V。不同加速度的输出电压-频率变化曲线和前一节特性分析中的动力学特性分析结果基本一致。因此，验证了实验结果的可信度，但由于仿真分析的开路输出电压是在理想情况下的，在实际的环境中所存在一定的偏差，以实验结果为主要参考依据。

图10 不同加速度的输出电压-频率曲线

压电材料厚度为0.2 mm且外激励加速度为1.0g时，当俘能器末端安装不同质量的质量块时(2.0、4.0、6.0 g)，梯形悬臂梁压电俘能器的输出电压-频率曲线如图11所示，当质量是2.0 g时，俘能器的一阶固有频率为57 Hz，最大输出电压为8.56 V；当质量是4.0 g时，俘能器的一阶固有频率为46 Hz，最大输出电压为10.22 V，当质量是6.0 g时，俘能器的一阶固有频率为40 Hz，且最大输出电压为6.84 V。随着质量块数量的增加，俘能器的一阶固有频率逐渐降低，而俘能器的输出电压先增加后减少。

图11 不同质量块的输出电压-频率曲线

压电材料厚度为0.2 mm，加速度为1.0g时，梯形悬臂梁压电俘能器外接不同负载时(1、2、3、4 kΩ)的输出功率-频率曲线如图12所示，当外接负载为1 kΩ时俘能器最大输出功率为451.62 μW，当外接负载为2 kΩ时俘能器最大输出功率为201.44 μW，当外接负载为3 kΩ时俘能器最大输出功率为78.72 μW，当外接负载为4 kΩ时俘能器最大输出功率为19.53 μW。

图12 不同外接负载的输出功率-频率曲线图

4 结论

本文提出一种梯形悬臂梁压电振动俘能器结构，对其进行力学特性分析和机电耦合特性分析，并进行了实验测试，得出如下结论：

(1)梯形悬臂梁单位体积输出电压是131 V/m3，矩形悬臂梁单位体积输出电压是76 V/m3，梯形悬臂梁的能量密度是4 673 μW/m3，矩形悬臂梁的能量密度是2 600 μW/m3，与矩形悬臂梁压电振动俘能器相比，梯形悬臂梁压电振动俘能器有一阶固有频率低、压电材料利用率高、单位体积内输出电压高以及能量密度高等优点；

(2)在弹性基体的厚度不变的情况下，随着压电材料厚度的增加，梯形悬臂梁压电振动俘能器的一阶固有频率也会增加，而最大输出电压和最大输出功率逐渐减小，压电材料厚度对一阶固有频率、最大输出电压和最大输出功率有较大影响；

(3)梯形悬臂梁压电振动俘能器的输出功率随外接负载的增加而逐渐减小；

(4)对梯形悬臂梁进行电压和功率测试，实验结果与仿真分析相吻合，实验结果表明：压电材料厚度为0.2 mm，加速度为1.2g，末端质量块为4.0 g时，梯形悬臂梁俘能器的最大输出电压为13.8 V。