基于LSTM的气液两相流液相流量测量方法
2021-11-29仝卫国曾世超李芝翔朱赓宏
仝卫国,曾世超,李芝翔,朱赓宏
(华北电力大学控制与计算机工程学院,河北保定 071003)
0 引言
气液两相流广泛存在于石油、冶金、火力等工业生产中,精确且快速的流量参数测量有助于提高工业系统运行的稳定性[1-3]。电阻层析成像技术通过还原待测介质的电导率分布,且具有非侵入性、响应速度快、结构简单等优点,因此被广泛应用于两相流的可视化监测中[4-5]。传统流量测量仪表的测量对象主要是液体或气体等单相流体,局限性较大。新技术流量仪表如电磁流量计、超声波流量计等,其测量精度高、测量速度快,满足了工业生产在线测量和可视化监测的需求[6-7]。
近年来,神经网络在流量测量领域得到了大量研究。匡世才[8]等利用BP(back propagation)神经网络构建了集输-立管系统的气液两相流流量测量模型;张怡[9]等建立了3层Elman神经网络模型,将其与弯管流量计结合,有效提升了煤粉颗粒质量流量测量精度;张晓钟[10]等通过分析轻质燃油内超声波的传播速度、温度和介质密度的关系,利用人工神经网络建立模型,完成了轻质燃油的质量流量测量。
ERT系统多用于两相流流型图像重建及流型识别,对液相流量的测量准确性不高。为提高气液两相流液相流量测量的准确性和及时性,提出了一种基于ERT系统和LSTM神经网络相结合的气液两相流流量测量方法。利用顺序排列的16电极依次激励得到的120个电阻值作为LSTM网络的输入,以电磁流量计采集的液相体积流量作为理想输出。实验表明,本文提出的方法在两种流型下平均引用误差低于3%。
1 ERT系统测量原理
典型的ERT系统主要包括传感器单元、数据采集与处理单元和计算机图像重建单元。典型的ERT传感器金属电极数目有8、12、16个,阵列传感器被安装在管道外围且呈等间隔排列。由于金属电极对待测介质的变化十分敏感,因此电阻数值与介质分布有一定相关性。电阻值的测量数量是由电极数量决定的,其计算公式如式(1)所示。
N=0.5×n×(n-1)
(1)
式中:N为可测的电阻值数量;n为ERT系统的阵列电极数量。
本实验采用的16电极的ERT系统电极测量结构如图1所示,通过对16个电极依次施加激励信号,即可得到120个电阻测量值。ERT系统中高灵敏、高信噪比的数据采集与处理单元将获取的信号传输到计算机,经过图像重建算法便能够重建被测介质的电导率分布状态。
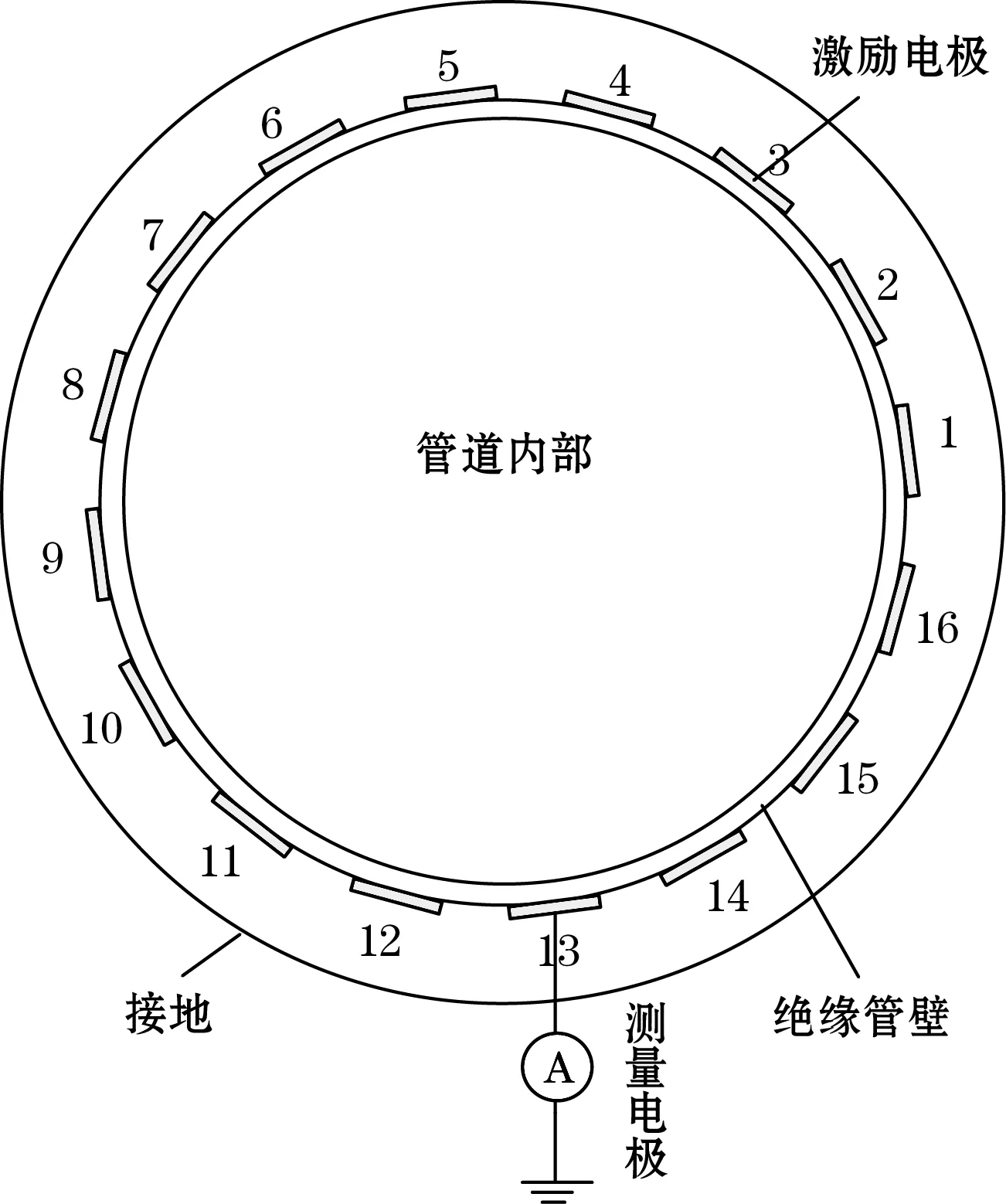
图1 ERT系统16电极测量结构图
2 基于LSTM的气液两相流液相流量测量模型
2.1 LSTM神经网络模型
标准循环神经网络(recurrent neural network,RNN)适用于处理序列数据,由于RNN在每层及每个神经元间都建立了权连接,使得每个神经元的当前输出依赖于当前网络输入与之前网络输出。但当序列数据足够长时,RNN的网络结构会随之加深,进而出现梯度爆炸和梯度消失的问题。LSTM循环神经网络利用“门”的内部机制来调节网络内部信息流,很好地解决了标准RNN的短时记忆问题,如今LSTM已经被广泛应用在参数预测[11-14]、文本分析[15]等领域中。
LSTM单元包括输入门it、遗忘门ft、输出门ot,其中输入门it和遗忘门ft的引入能够使得RNN更有效地保留长期记忆,LSTM单元细节图如图2所示。输入门it通过运算能够控制当前时刻的输入数据xt流入记忆单元Ct的数量;遗忘门ft通过运算来调节之前时刻信息Ct-1对当前时刻Ct的影响,即实现序列信息的保留和遗忘;输出门ot通过运算调节Ct对当前时刻输出值ht的影响。
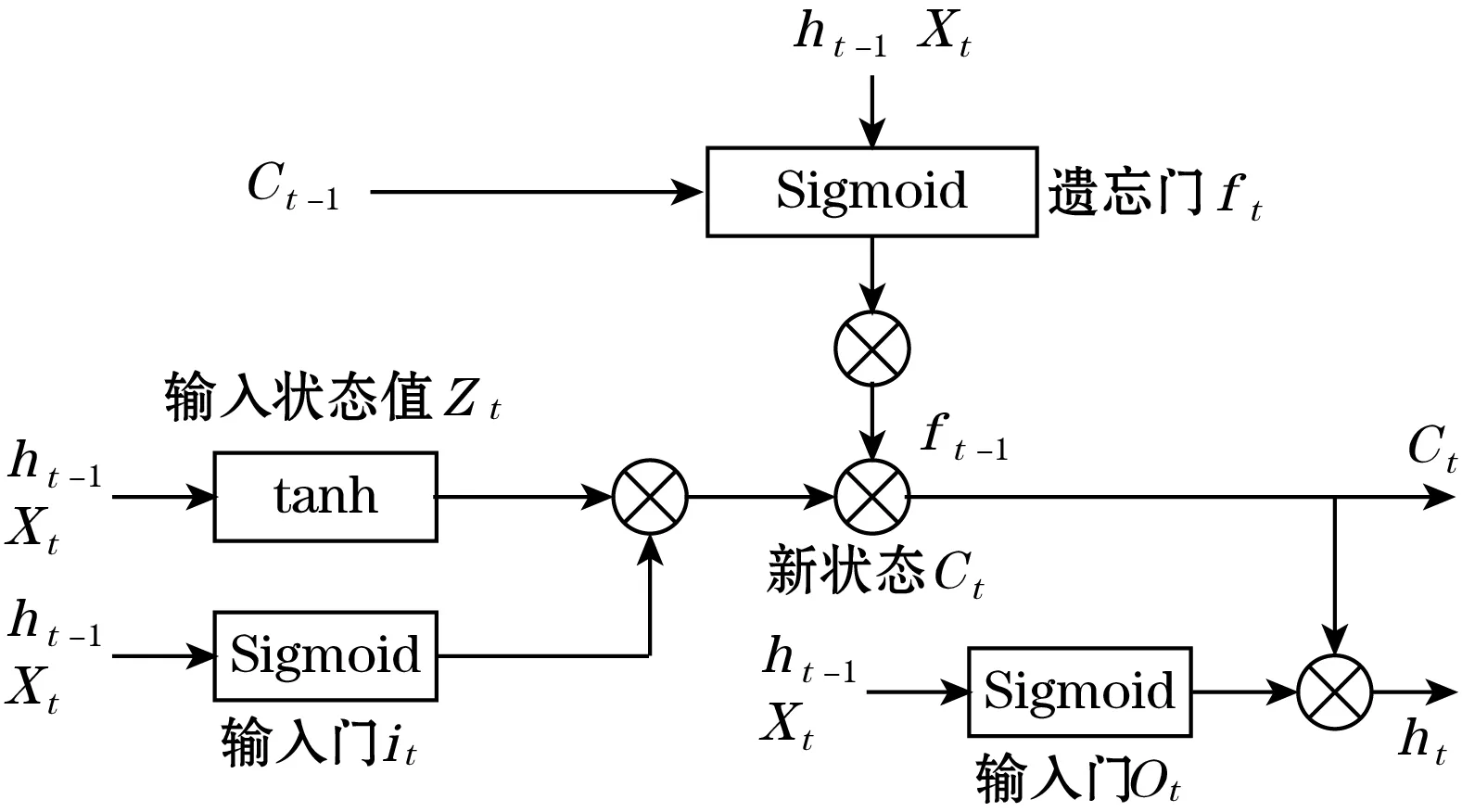
图2 LSTM单元结构图
图2中,ht为当前时间点输出,ht-1为前一个时间点输出,xt为当前时间,sigmoid和tanh为激活函数,具体运算可以参照式(2)~式(6)。
Ct=ft×Ct-1+it×Zt
(2)
ft=sigmoid(W[ht-1,xt]+bf)
(3)
it=sigmoid(W[ht-1,xt]+bi)
(4)
ot=sigmoid(W[ht-1,xt]+bo)
(5)
Zt=tanh(W[ht-1,xt]+bz)
(6)
式中:W和b分别表示相应的门权重和门偏置。
16电极的ERT系统能够采集到某时刻的120个电阻值信息,且电阻值中包含一定的时间变化,能够体现内部介质的流动情况,因此能够利用120个电阻值信息和LSTM神经网络构建气液两相流液相流量测量模型。
2.2 数据集构建及预处理
启动水泵等待管道内水满管后,通过气泡发生装置能够调节管道内进气量的大小和进气间隔,进而产生不同的气液两相流流型。当进气量较少时,管道中会产生泡状流;当加大进气量并改变进气间隔后产生弹状流。图3为ERT系统重建的两种流型图像。
本次实验在气液两相流实验装置中采集了24 000组流型特征电阻值及对应的液相流量值,其中弹状流和泡状流各12 000组,两种流型数据中11 760组用作训练,剩余240组用作测试。为方便后续数据处理及保证神经网络运行时收敛加快,需要对数据集进行归一化预处理,使原数据通过线性变换映射到0~1之间。设原始特征电阻值为ri,j(1≤i≤120,1≤j≤24 000),归一化预处理公式如下:
(7)
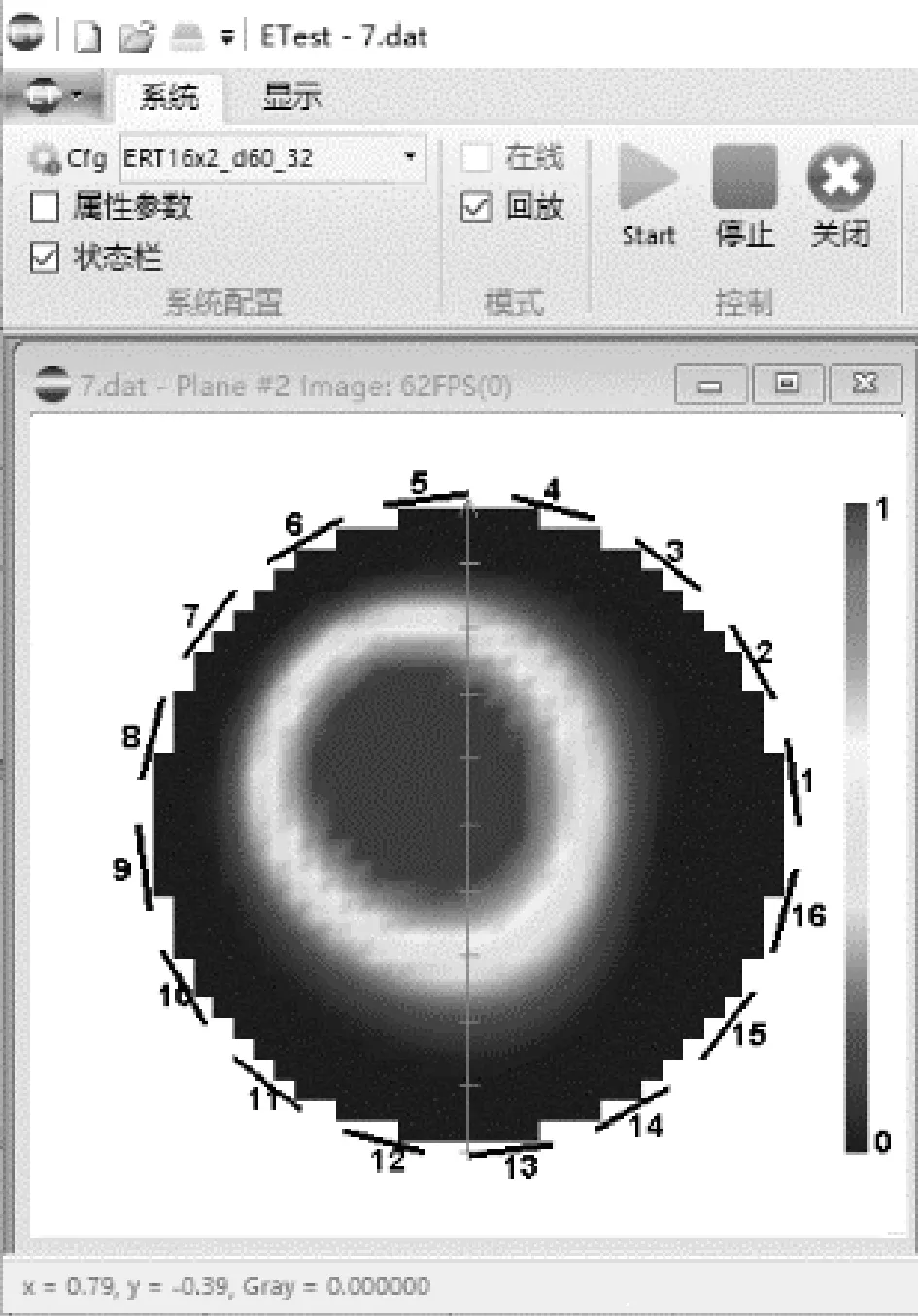
(a)弹状流图像
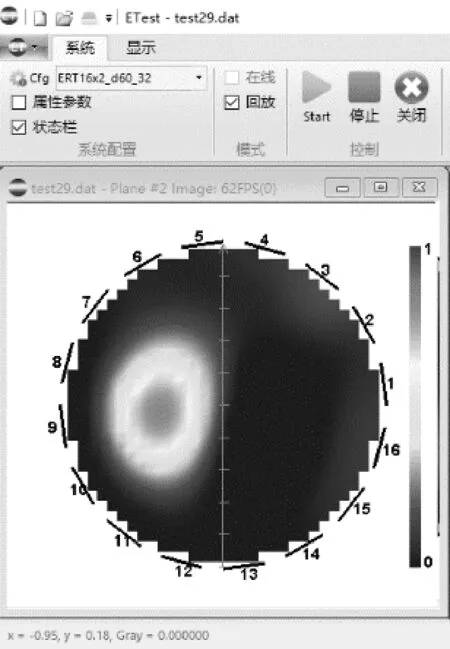
(b)泡状流图像
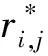
2.3 气液两相流液相流量测量模型的构建
基于LSTM气液两相流流量测量模型一共可以分为输入层、LSTM层、Dropout层、全连接层和输出层。而LSTM层由多个LSTM堆叠而成,具体结构参照图4所示。

图4 基于LSTM的气液两相流流量测量模型
首先将经过归一化处理的电阻值数据排成120×23 520的特征向量矩阵,接着输入层将数据传入单元数为200的LSTM层。多层LSTM结构能够加深网络结构,使得模型能够学习到数据集的深层特征。
Dropout层的设置目的是降低神经元节点间的相互依赖性,有助于实现网络的正则化并降低网络结构风险,实验中Dropout层的丢弃概率为0.5。最后由全连接层通过线性变换将网络输出转为1个一维标量,即液相流量测量值,并以该测量值为最终输出。
3 实验结果与分析
3.1 实验环境
本实验采用的流体流动管道为80 mm不锈钢管道,ERT的16电极等间距排列在DN60的竖直有机玻璃管道上,并进行顺序编号。电磁流量计的量程为0.5~120 m3/h,准确度为0.5级。ERT系统通过电缆连接到计算机上,使用TJU-Etest软件收集特征电阻值。基于LSTM的气液两相流液相流量测量模型的训练平台为MATLAB/CPU:Intel Core i5-10400F @2.9GHz/GPU:Nvidia GeForce RTX 2060。
3.2 评价标准
由于电磁流量计采集的液相流量值变化幅度大(0.5~120 m3/h),为客观评价构建模型的测量精度,采用均方根误差(root mean square error,RMSE)和平均引用误差(mean citation error,MCE)作为评价标准,计算式参照式(8)、式(9)。
(8)
(9)
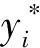
3.3 不同LSTM层数对流量测量精度的影响
相较于单层LSTM,多层LSTM能够加深网络结构,提高神经网络的非线性拟合效果。为探究LSTM层数对流量测量模型精度的影响,将网络中LSTM的层数分别设置为2、3、4层。通过搭建不同LSTM层数的流量测量模型并进行训练,利用相同数据集进行测试,泡状流和弹状流预测结果如图5、图6所示,具体测试结果评价指标如表1所示。
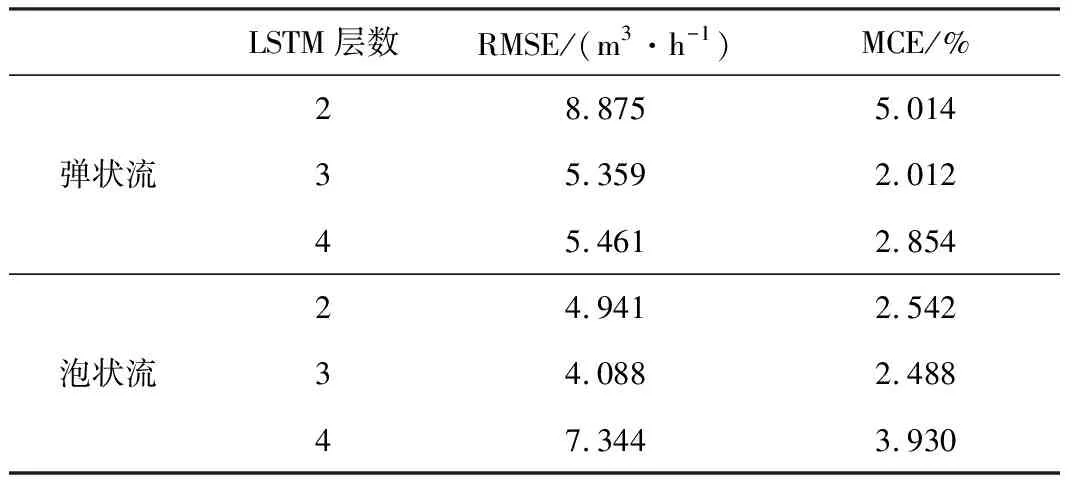
表1 不同LSTM层数及模型精度
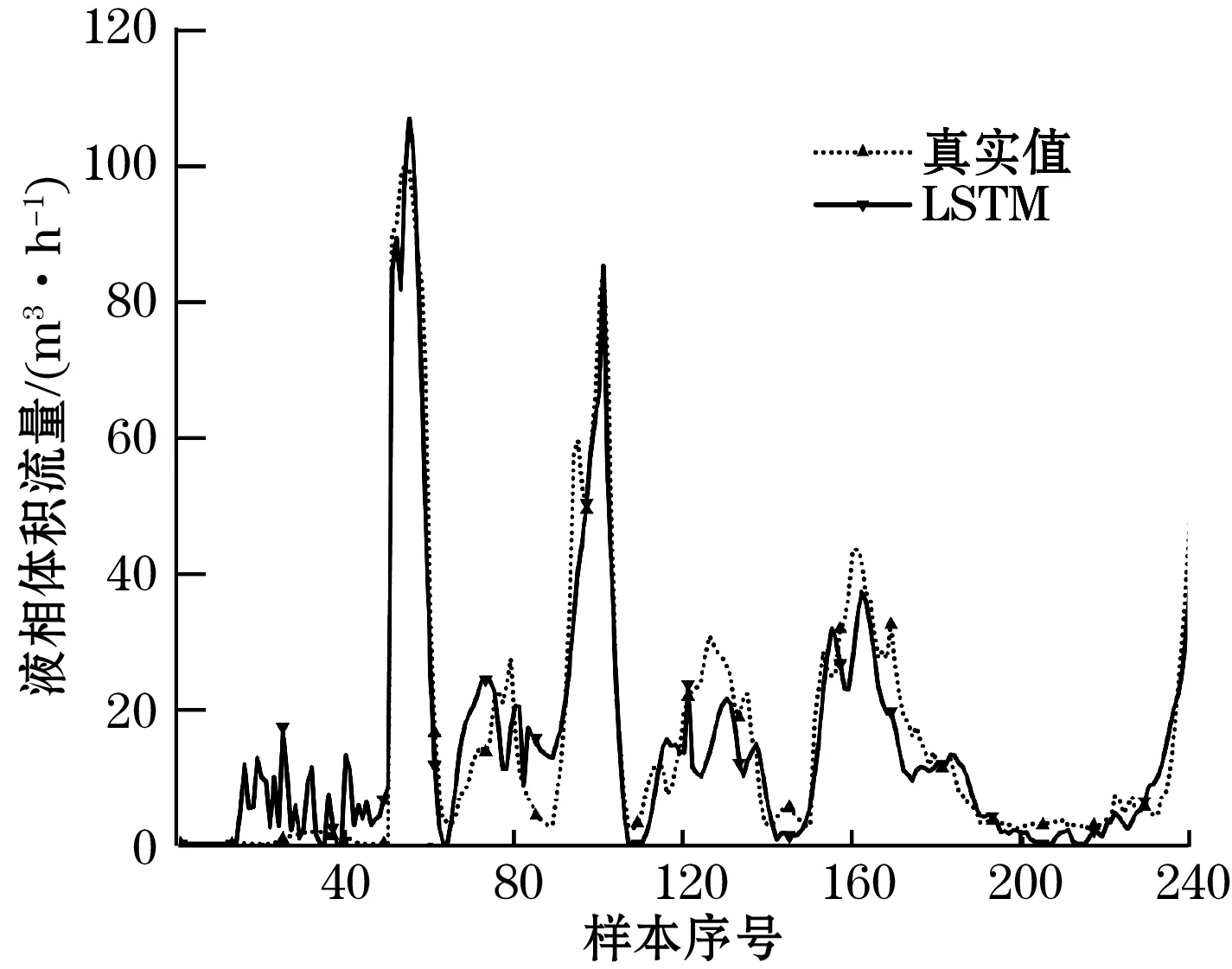
(a)LSTM层数为2
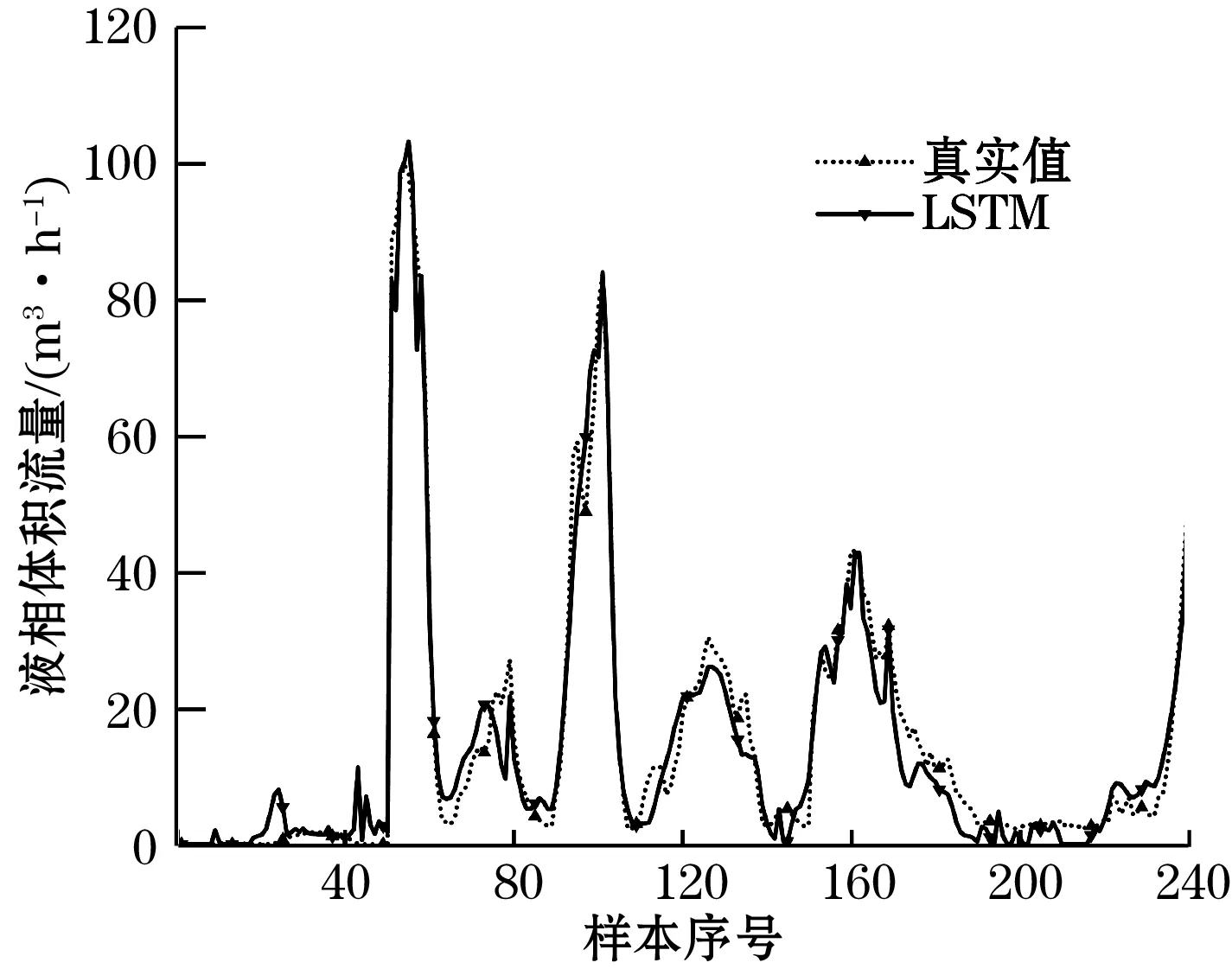
(b)LSTM层数为3

(c)LSTM层数为4图5 不同LSTM层数泡状流测量结果
由表1可知,适当增加LSTM层数能够有效提升模型的测试精度。当LSTM网络层数为3时,RMSE和MCE均为最小值,表明该模型在泡状流和弹状流流量测量中取得了较好效果。当LSTM网络层数进一步增加到4,并没有获得更好的模型精度,反而增加了计算冗余。因此,考虑到测量精度及测量速度,本文模型选择的LSTM层数为3。
3.4 BP神经网络对比实验结果与分析
为比较LSTM神经网络模型的性能,构建单隐含层的BP神经网络对相同的数据集进行训练和测试。BP神经网络的输入层、隐藏层和输出层神经元数分别为120、200和1。BP神经网络在2种流型下的测量结果如图7、图8所示。
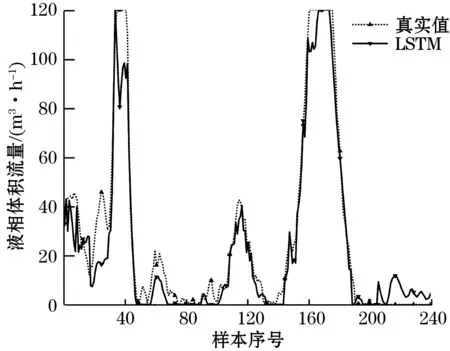
(a)LSTM层数为2
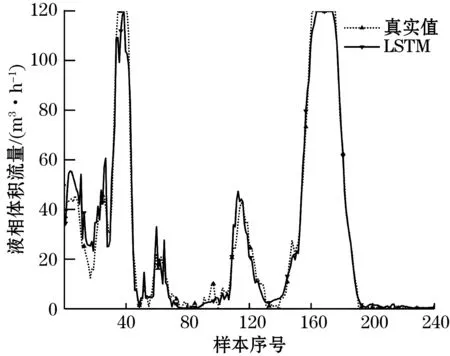
(b)LSTM层数为3

(c)LSTM层数为4图6 不同LSTM层数弹状流测量结果
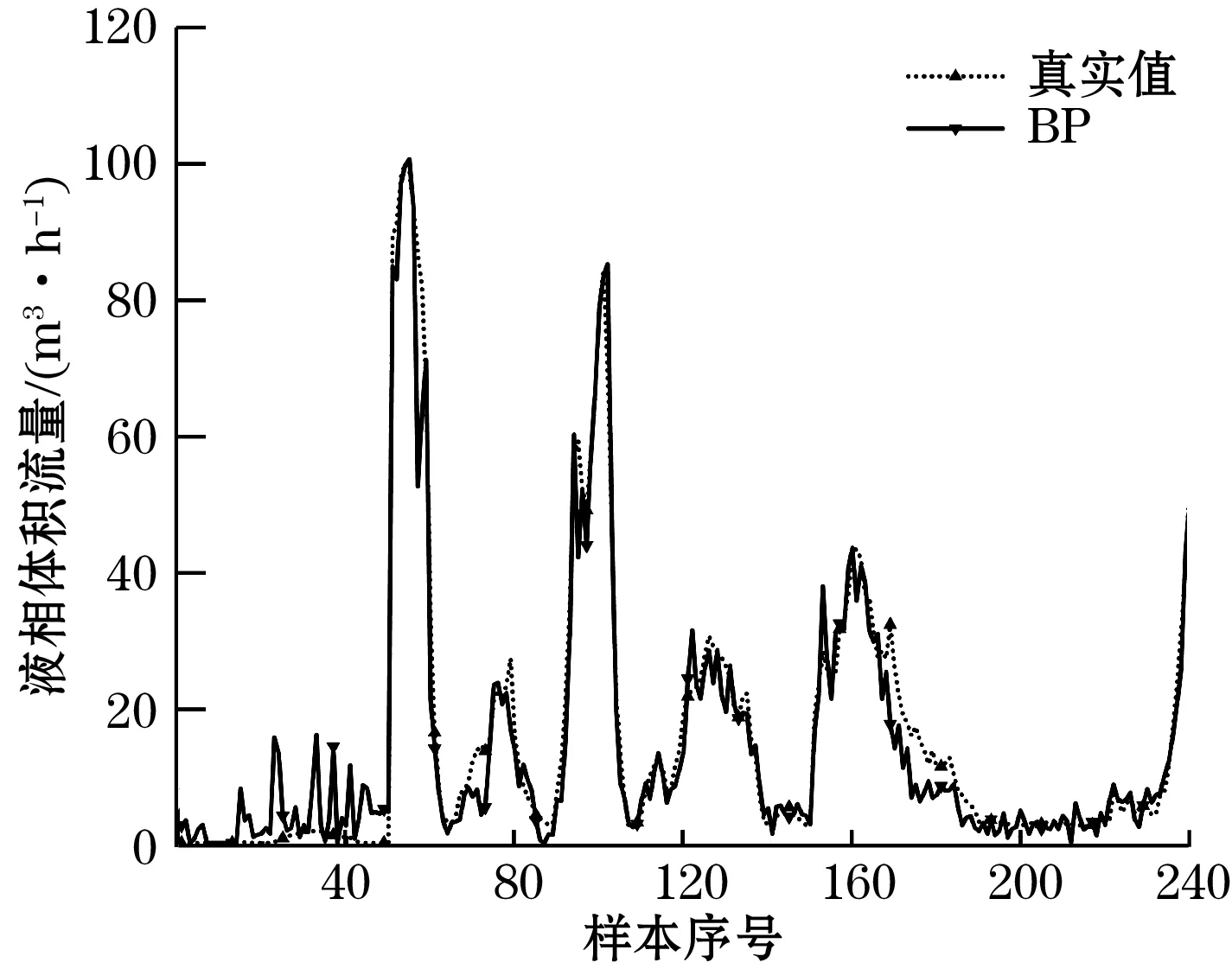
图7 BP神经网络泡状流测量结果
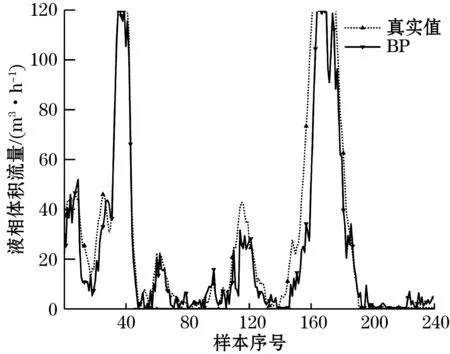
图8 BP神经网络弹状流测量结果
可以看出3层LSTM的测量效果优于BP神经网络,泡状流中RMSE和MCE分别降低了2.665 m3/h和1.69 %,弹状流中RMSE和MCE分别降低了6.618 m3/h和3.574 %。且在训练BP神经网络的过程中,由于数据集庞大且神经元节点偏多,训练及测试耗时远高于LSTM神经网络。
4 结束语
提出了一种基于16电极ERT系统采集阵列电阻值和LSTM 神经网络相结合的气液两相流液相流量测量方法。研究了不同LSTM层数对模型测量精度的影响,确定了输入样本为120个阵列电阻值,LSTM层数为3。与BP神经网络进行对比实验,表明本文提出模型测量精度和测量速度均优于BP神经网络。
此方法保留了原始样本数据集的全部特征,并利用LSTM学习电阻值的深层特征,解决了传统神经网络应用于流量测量训练耗时长、精度低的问题,实现了对气液两相流液相体积流量的准确测量,为后续研究深度神经网络在流量测量的应用提供了一定的参考。
