基于小波变换的白酒检测电子鼻降噪方法研究

孙哲华，孟庆浩，靳荔成

(天津大学机器人与自主系统研究所，天津市过程检测与控制重点实验室，天津大学电气自动化与信息工程学院，天津 300072)

0 引言

近年来，电子鼻技术的研究和应用逐步成为国内外的研究热点，在汽车[1]、农业[2]、食品[3]、医药[4]、环境保护[5]等领域都有较为广泛的应用，但是国内的电子鼻技术大部分仍处于实验室阶段，阻碍电子鼻技术发展的一个很重要的因素是电子鼻采用的金属氧化物型气敏传感器精度较低，会受到许多形式的噪声干扰，噪声的来源主要有传感器长期使用产生的漂移噪声以及环境对传感器产生的噪声[6]，较大的噪声会严重影响电子鼻的分类精度，因此，对于如何去除或降低电子鼻信号中的噪声显得十分重要。

为消除电子鼻中噪声的影响，屈剑锋[7]等提出了一种能够自适应调整测量方差以及去除非高斯噪声的自适应卡尔曼滤波算法，去除了电子鼻采样过程中的传感器噪声信号，提高了识别精度。袁桂玲[8]等人利用独立分量分析的方法，对传感器阵列信号进行分解，去除了外界干扰噪声，对气体成分的识别达到了较好的效果。马泽亮[9]等使用传感器阵列获得白酒“指纹数据”后，通过离散小波变换对数据进行预处理，采用波形相似系数作为指标，选择出了最优的小波系数和分解层数，结合主成分分析实现对白酒真假的快速鉴别。J. Feng等人[10]以小鼠为实验对象研究基于电子鼻的伤口感染检测，采用小波分析对传感器阵列的每个信号进行分解，将受伤和健康小鼠的反应信号在相应尺度上的小波变换系数直接相乘，有效地消除了小鼠自身气味的影响。S. Osowski等[11]分析了电子鼻识别汽油生物基添加剂时的畸变数据，采用基于Haar小波的软阈值函数离散小波去噪方法对畸变数据进行了降噪处理，降低了识别的错误率。

目前的研究中，小波变换常用于电子鼻数据的降噪，但小波降噪方法中常用的软阈值函数和硬阈值函数存在着一定的缺点：硬阈值函数降噪之后仍保留有尖刺和振荡，降噪效果较差，而软阈值降噪后虽然曲线较为平滑，但同时也对有效信号造成了一定的损伤，且阈值函数无法根据噪声的不同进行调整，为了解决这一问题，本文基于小波降噪中的软、硬阈值函数提出了一种改进的阈值函数，通过仿真和实验验证了基于改进的阈值函数的小波降噪方法的有效性，最后将其应用于电子鼻采集的白酒数据中，通过主成分分析法[12]比较了4种不同的降噪算法的降噪效果，验证了基于改进的阈值函数的小波降噪方法对白酒电子鼻数据降噪的可行性。

1 实验仪器与方法

1.1 白酒检测电子鼻系统

本文使用的由实验室自行研制的白酒检测手持式电子鼻系统主要包括ARM(advanced RISC machines)系统板、气室、气路系统、LCD(liquid crystal display)触摸屏等部件，该系统采用动态顶空采样方法，设计了泵吹式的气路系统。系统所使用的传感器阵列是由6种MOS(metal oxide semiconductor)型气体传感器构成，分别是CCS801和CCS803，TGS8100，MiCS-5914、MiCS-5524和MiCS-4514，各型号传感器对应的典型敏感气体如表1所示。另外还配有温湿度传感器SHT21用于测量环境温湿度，在做实验时尽量保持环境温湿度的一致，以防温湿度变化对传感器的响应造成影响。

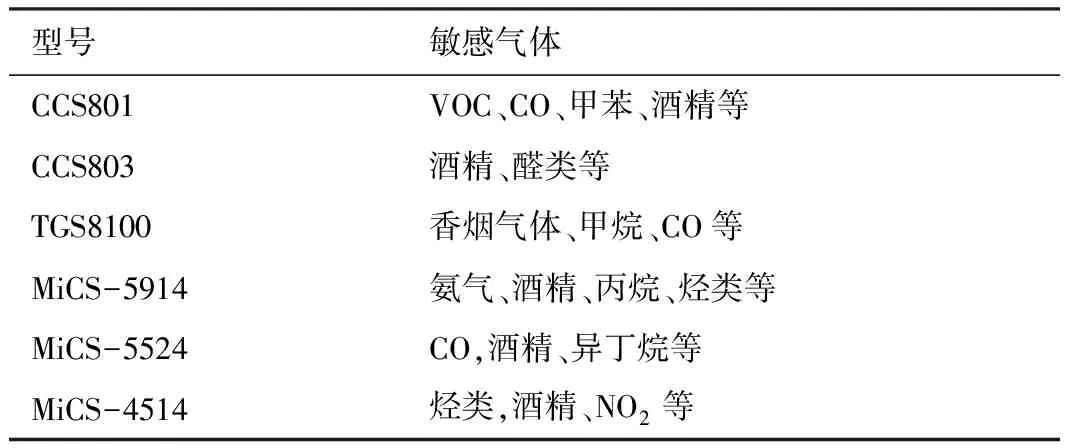
表1 气体传感器与典型敏感气体

1.2 实验材料

实验中使用了6种不同的白酒，所属香型、酒精度数以及产地都各有不同，包括汾酒、国窖1573，剑南春，飞天茅台，五粮液和西凤酒。实验时室内温度为28 ℃，相对湿度为30%RH，电子鼻采样频率为400 Hz，采样时间为40 s。其中采集基线的时间为4 s，吸气时间(向气室中吹入待测气体的时间)为1 s，吸气等待时间为3 s，呼气时间(从气室中吹入洁净空气的时间)为32 s。测试结束后持续向气室中通入洁净的空气30 s，使各传感器回复到基值状态，以便于下一个样本的测量。

2 离散小波变换降噪

2.1 离散小波变换降噪过程

离散小波变换(discrete wavelet transform，DWT)是一种基于多分辨率分析和多采样率滤波器理论的算法。常用于非平稳信号分析和局部特征提取[13]，其原理如图1所示。图中，P[n]为带有噪声的原始信号，g[n]为低通滤波器，h[n]为高通滤波器，带有噪声的原始信号通过2种滤波器进行分解后，会得到2组分量，低频分量部分Ai称为近似分量，而高频部分Di称为细节分量，由于噪声的频率一般是高于有效信号的频率，所以有效信号一般是位于近似分量中，再对近似分量进行分解，可以进一步地提取出有效信息。而由于信号在空间上(或者时间域)具有一定的连续性，因此在小波域，有效信号所产生的小波系数的模值一般较大；而高斯白噪声在空间上(或者时间域)没有连续性，因此噪声经过小波变换后对应的系数很小[14]。需要通过一定的阈值选择方法，比如无偏风险估计阈值、固定阈值、启发式阈值等，将阈值以内的系数看做是噪声对应的系数，进行置0处理，其他系数通过一定的阈值函数进行处理，将经过阈值处理后的小波系数进行重构，就可以得到去噪后的信号，这样可以最大程度地抑制噪声，同时只损失一部分有效信号。

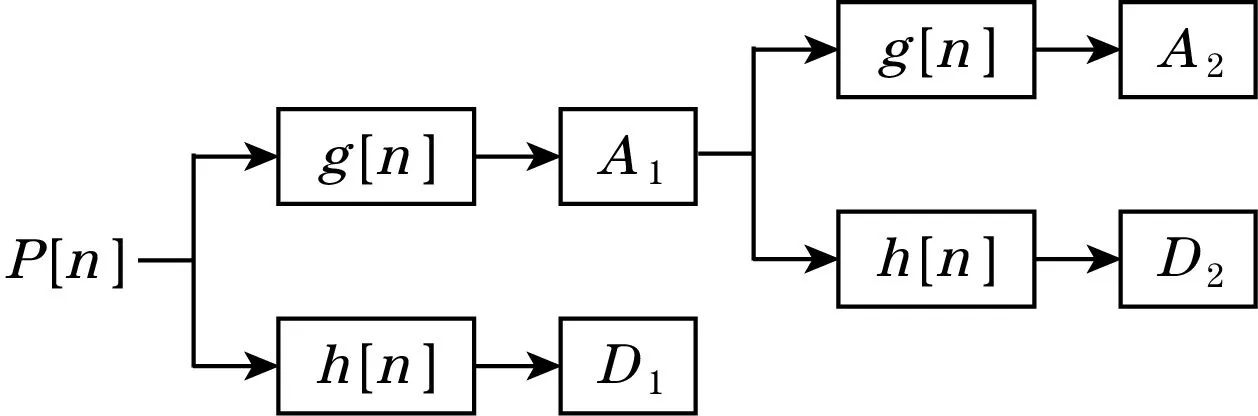
图1 DWT原理图

较为常用的阈值处理办法有硬阈值函数和软阈值函数[15]，硬阈值函数的基本思想是将阈值以内系数置0，阈值范围以外的系数不变，如式(1)所示：

(1)

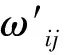
该种阈值算法由于会在小波域产生突变，从而导致去噪后信号产生局部的振荡，使得信号的光滑性变差，影响后续分析。而常用的软阈值函数则是将大于λ的系数统一减去λ，而小于-λ的系数统一加λ，如式(2)所示：

(2)

式中：sgn()为符号函数。

经过这种变换之后，去除了小波域中的突变，使得去噪之后的信号更为平滑，但缺点是需对小波系数进行较大的改变，从而丢失更多的有效信号，造成不可避免的误差，有着较大的信号失真。

2.2 改进的阈值函数

为了改善软、硬阈值函数的缺点，本文结合软、硬阈值函数的思想，提出了一种改进的阈值函数，改进的阈值函数如式(3)所示：

(3)

式中：a为调节因子，a>1。

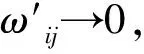
将改进的阈值函数和软、硬阈值函数在同一坐标系下表示(设阈值为2)，其对比如图2所示。从图中可以看出，当a值越大，改进的阈值越接近硬阈值函数，而当a值减少时，阈值函数的曲线变得更为平滑，更接近软阈值函数。改进的阈值函数融合了软、硬阈值函数的优点，在去除阈值附近的突变、保证函数连续性的同时，将不在[-λ，λ]之内的小波系数变化尽可能地减小，并且可以通过调整a值取得最佳的平衡点。这样就使得信号在经过重构之后既不会丢失太多的有效信息，同时也能减少振荡，达到更好的降噪效果。

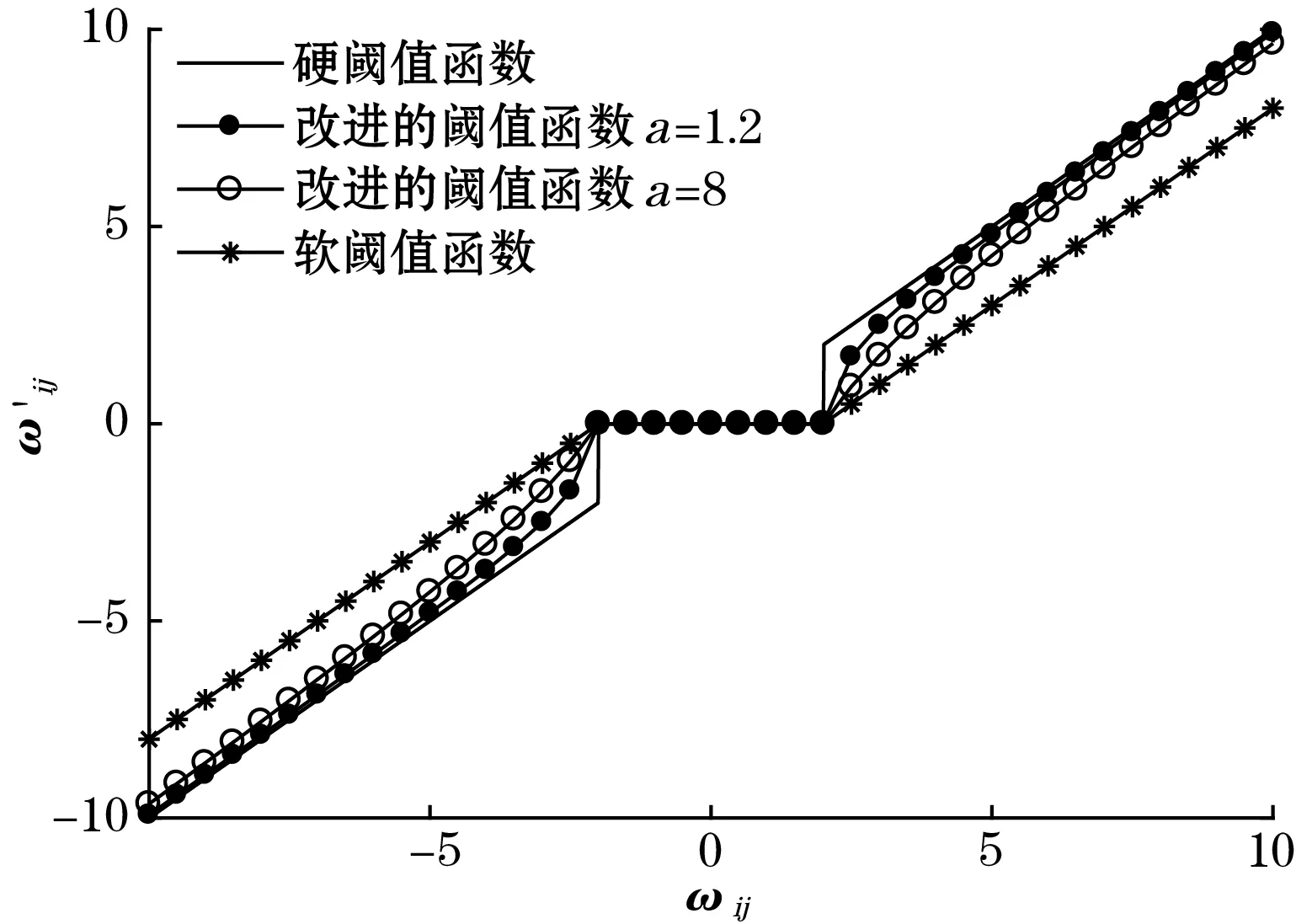
图2 改进阈值算法和软、硬阈值算法的对比图

3 仿真验证

为了对改进阈值函数的有效性进行验证，向1个原始信号中加入信噪比为10的高斯白噪声，原始信号和加入高斯白噪声的信号分别如图3(a)和图3(b)所示，原始信号中包含频率较低且较为平滑的正弦曲线部分，也包括2个跳变，对应白酒电子鼻检测信号中频率较低的有效信号曲线以及白酒电子鼻检测到敏感气体之后产生的响应值上升过程。其跳变部分以及正弦曲线顶点部分都是较为重要的信息点。

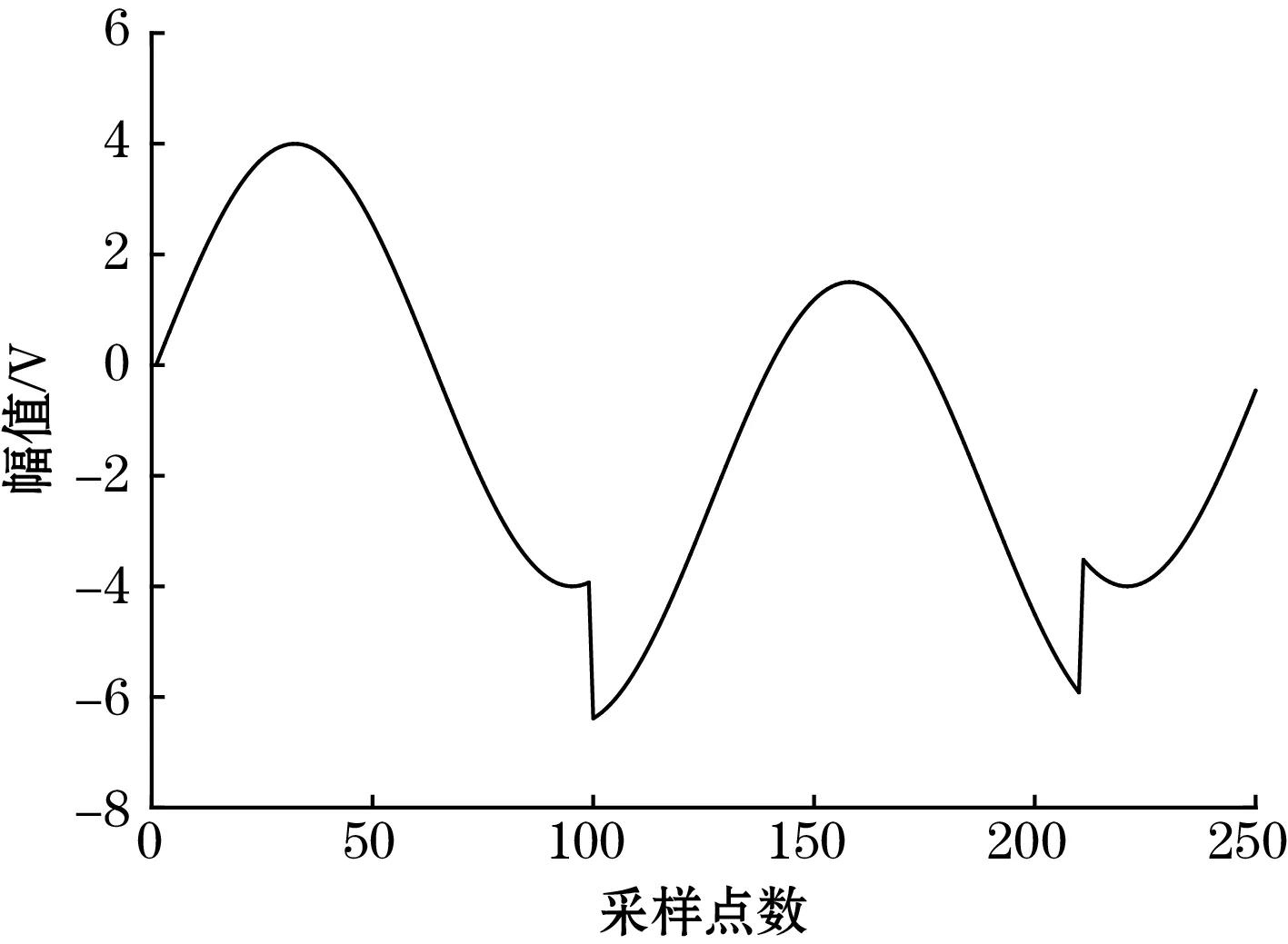
(a)原始信号

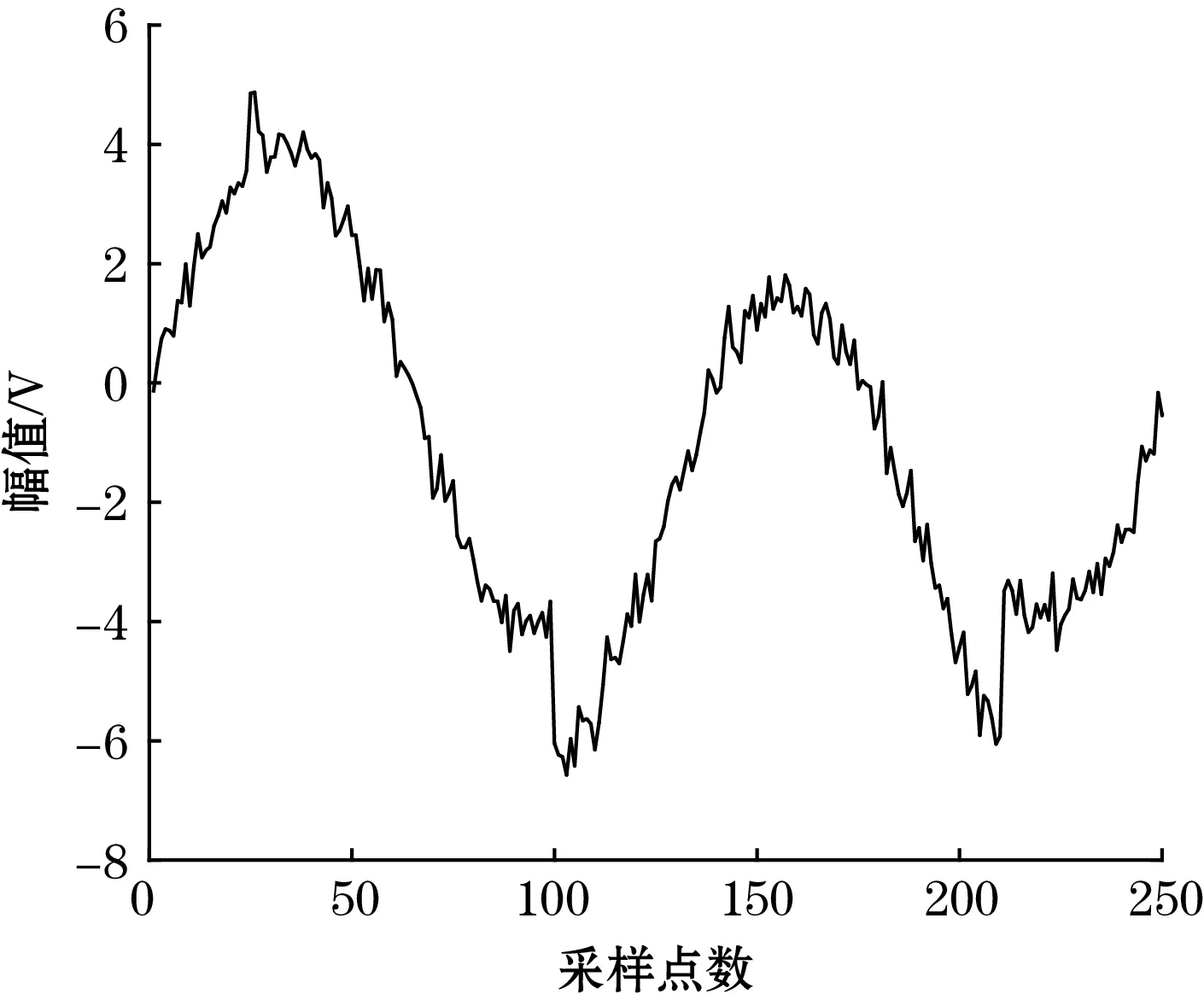
(b)加入噪声后的信号图3 原始信号和含噪信号

首先对含噪信号进行离散小波变换，采用较为常用的sym4小波基函数[9]，分解层数选择4，然后需要获取每层小波系数的阈值，阈值的获取方法为固定阈值法[16]，其表达式如式(4)所示：

(4)

式中：λ为该层的阈值；N为该层小波系数的个数；σ为该层小波系数的方差。

分别使用硬阈值函数、软阈值函数和改进阈值函数对系数进行处理，并通过计算实验的方式选出最佳的a值：a=1.2，最后通过逆变换实现降噪后信号的重构。3种不同阈值函数的降噪效果如图4所示。

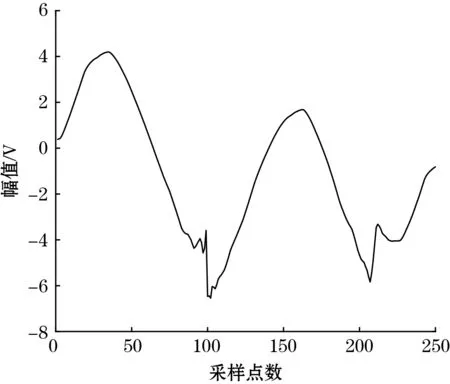
(a)改进阈值函数降噪效果

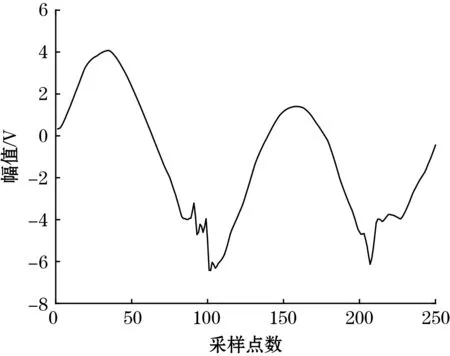
(b)硬阈值函数降噪效果

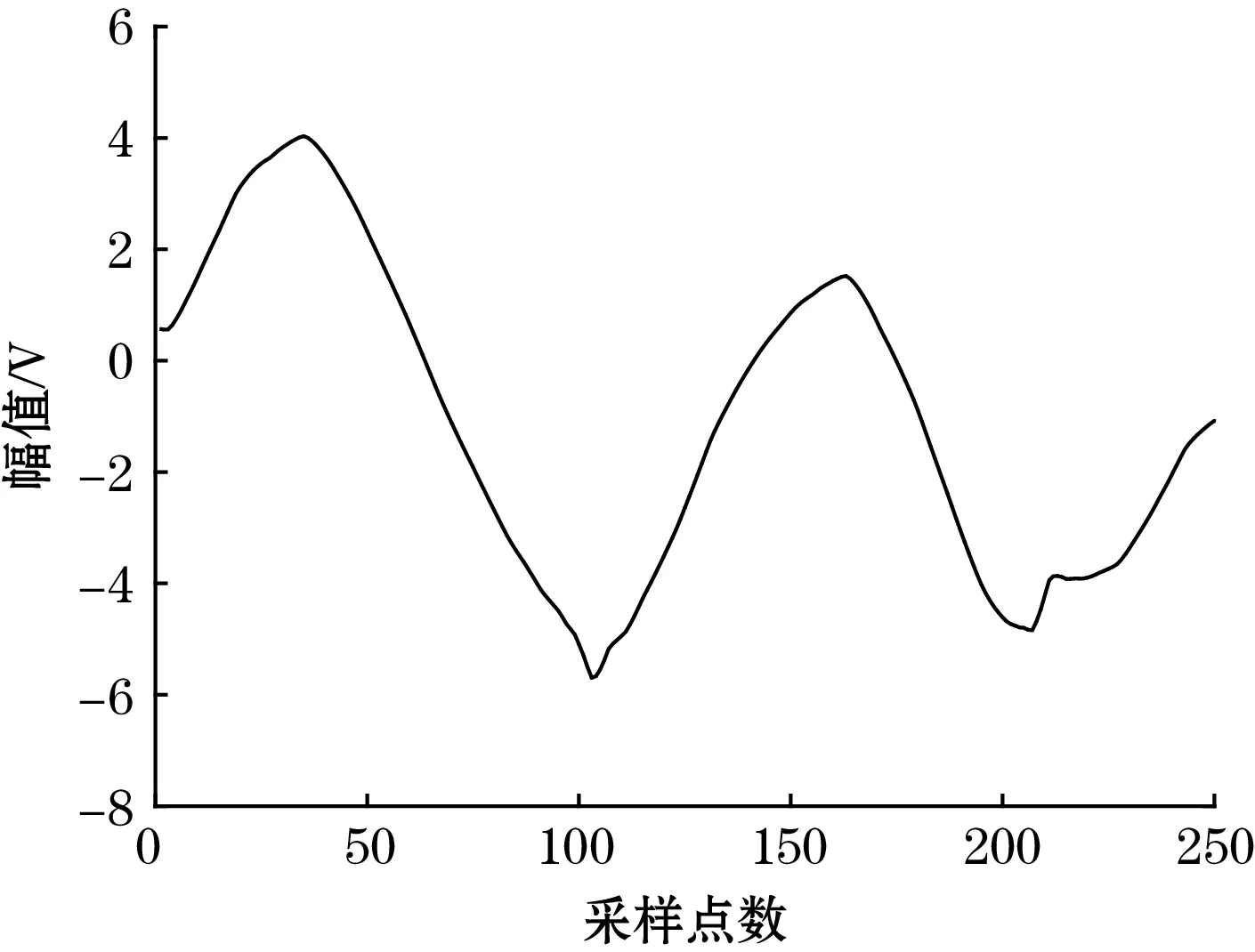
(c)软阈值函数降噪效果图4 不同阈值函数的降噪效果对比图

从图4可以看出，硬阈值函数降噪虽然在原信号突变处的效果还原较好，但是在降噪后的部分信号中仍保留着较大的振荡和尖刺，降噪后的信号平滑度较差，高斯白噪声加入的尖刺和振荡并没有完全去除；软阈值函数降噪后的信号平滑度得到了很大的提升，正弦信号的2个顶点的还原程度较高，但是2个突变处的信号还原程度较差，第1个突变部分已经很难看出，且第2个突变部分的幅值差也大大减小；改进的阈值函数降噪后的信号则较为完整的保留了2个突变处的信息以及正弦曲线较为平滑的部分，基本保留了原始数据的曲线，只存在小部分的小幅振荡，并且在两处突变的信息尽可能保留的前提下，去除了大部分由于高斯白噪声产生的尖刺和振荡。

信号的降噪效果也可以通过信噪比(signal-noise ratio，SNR)和均方根误差(root mean square error，RMSE)定量地评价[17]，信噪比和均方根误差的表达分别如式(5)和式(6)所示：

(5)

(6)

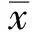
信噪比反映的是有效信息的“能量”和噪声的“能量”之间的比例，信噪比越大，则表示有效信息占的比例越多，即降噪的效果越好；而均方根误差则表示噪声的平均“能量”，均方根误差越小，噪声越少，降噪效果越好。基于软、硬阈值函数和a=1.2的改进阈值函数的小波降噪方法降噪后的信噪比和均方根误差如表2所示。

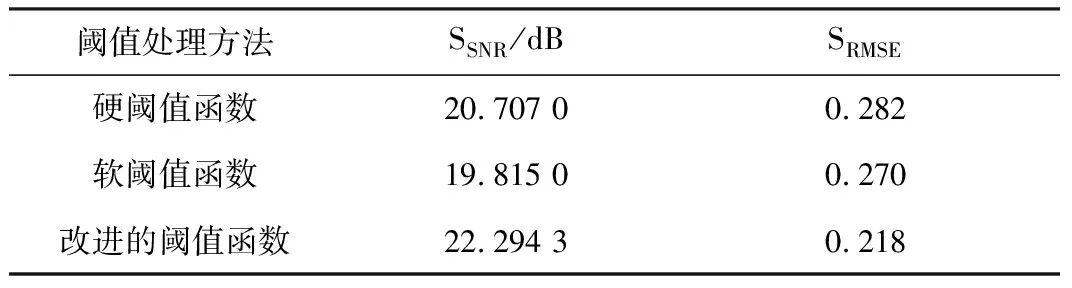
表2 3种不同阈值函数的降噪效果对比表

由表2可以看出，改进阈值函数降噪后的信噪比最高，均方根误差最小，说明不仅有效信号占比最高，并且噪声的“能量”最小。软阈值函数因为对信号的平滑处理过于严重，导致有效信号的大量减少，信噪比最低。硬阈值函数处理过后的信号由于尖刺较多，导致噪声的含量较高，信噪比也较低，并且均方根误差较大，降噪效果较差。

4 白酒电子鼻数据降噪处理

针对白酒检测电子鼻采集的六类白酒样本，分别使用改进的小波阈值函数降噪方法、软阈值函数小波降噪方法、硬阈值函数小波降噪方法以及中值滤波加SG (savitzky-golay)滤波(先中值滤波再SG滤波)的方法[18]对其进行降噪处理，以验证改进的阈值函数降噪方法的有效性。其中小波降噪方法均以“sym11”作为小波基函数，分解层数为7层，阈值的获取方法仍为固定阈值法，改进的阈值函数的a取5.2(以上各参数均由计算试验的方法获得)。中值滤波函数的窗口长度为51，SG滤波的窗口长度为71，多项式阶数为3[18]。数据处理软件平台采用MATLAB2017a。以CCS803的一次测量曲线为例，4种降噪方法的降噪效果如图5所示，信号在5 s左右和8.75 s左右的峰值已标出。

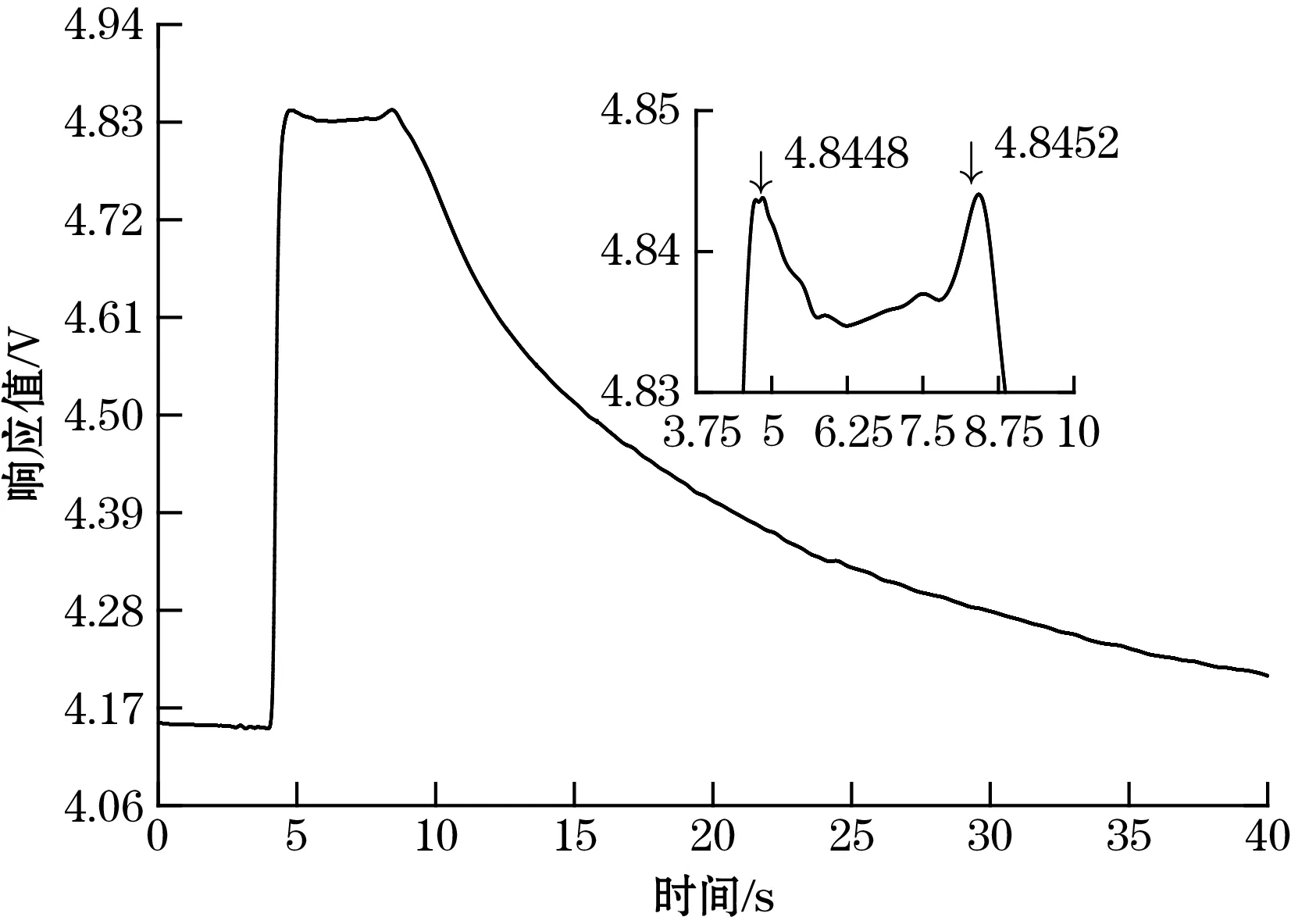
(a) 软阈值函数降噪

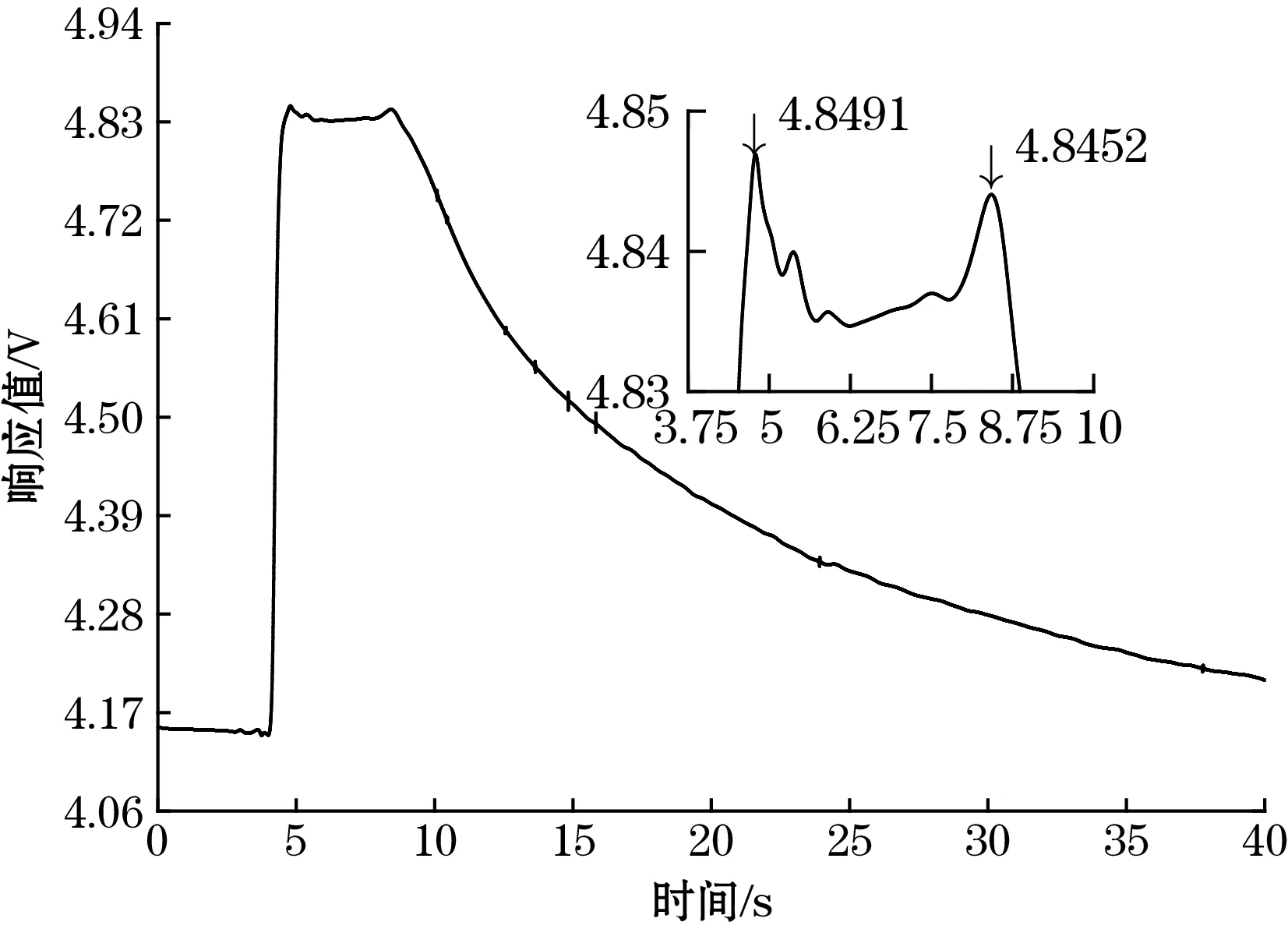
(b) 硬阈值函数降噪

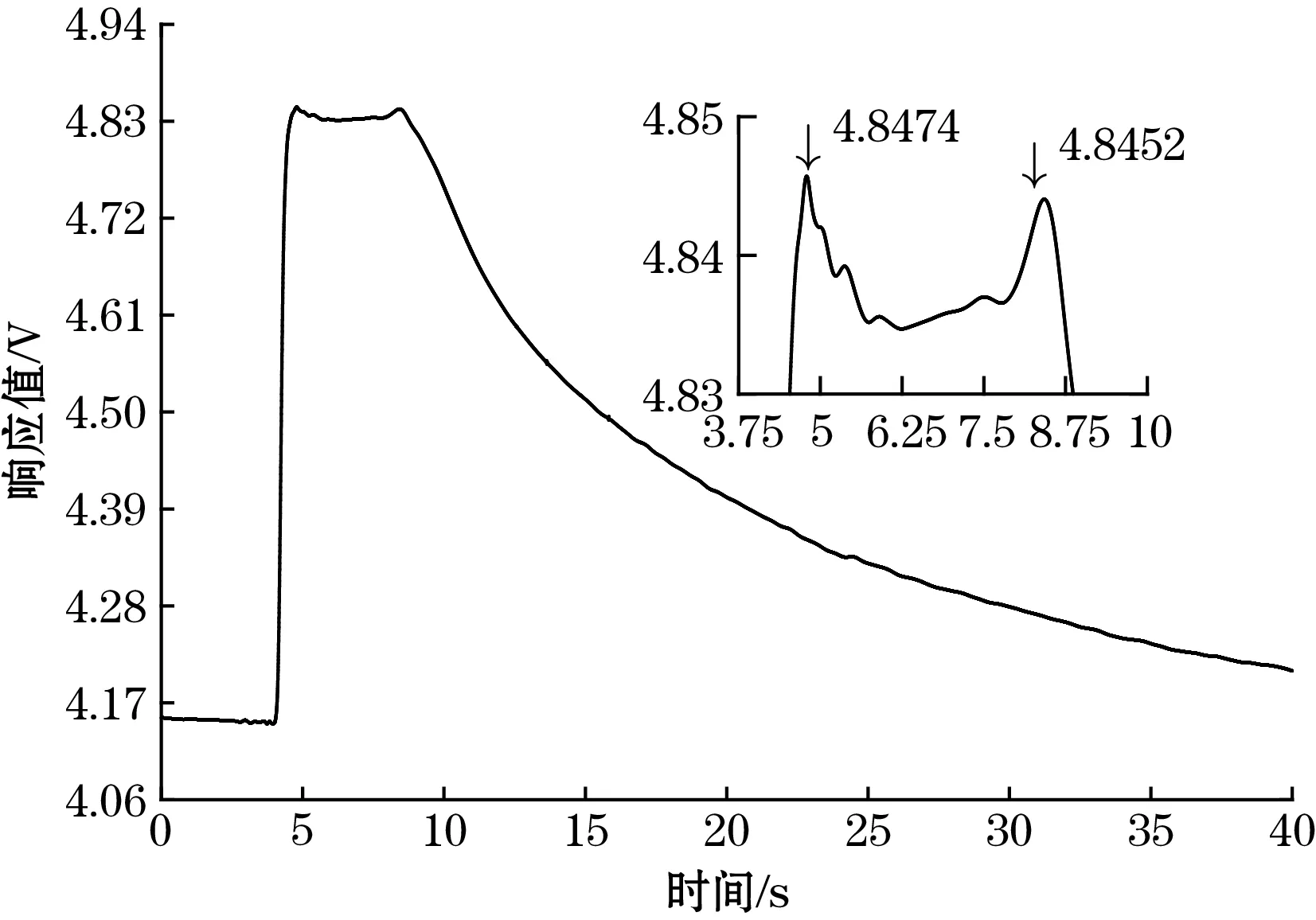
(c) 改进的阈值函数降噪

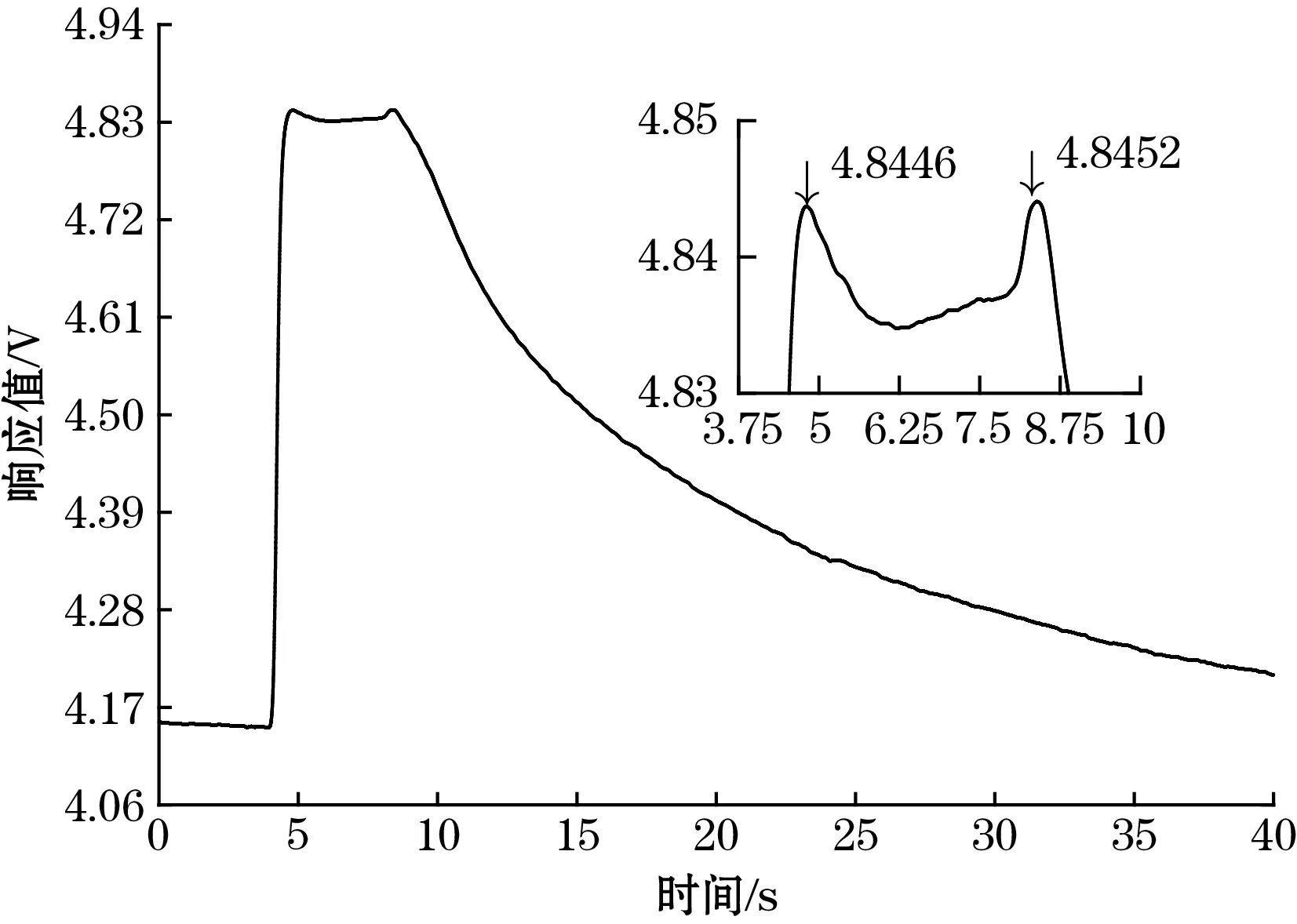
(d) 中值加SG滤波降噪图5 4种降噪方法的降噪效果图

从图5可以看出，硬阈值降噪后的信号中在15 s左右仍存在一些尖刺噪声，降噪的效果较差；软阈值函数降噪之后的信号较为平滑，但是在5 s左右的峰值要比其他的阈值函数降噪后的峰值要小，并且小于8 s左右的峰值，由于电子鼻系统采用先吸气1 s后保持3 s的采集流程，所以传感器响应的最高值应该出现在第一次峰值出现的时刻，对于CCS803即为5 s左右，8 s左右出现的尖峰可能是由于气体流速增大导致的信号值上升[19]，如果算作最大值，则会导致提取的特征不准确；从6.25 s至8 s处的信号平滑程度来看，中值滤波加SG滤波降噪后的信号最为平滑，但是同样出现了5 s左右的峰值小于8 s左右的峰值的问题；改进的阈值函数降噪后的信号较为平滑，并且5 s左右的信号值大于8 s左右的信号值，不会造成提取特征不准确的问题。

总体来看，硬阈值降噪的效果最差，其他3种降噪方式对于噪声的去除效果较好，但是由于无法得知传感器真实的响应，所以对于真实信号是否有损耗则无法看出，所以采用对降噪后的数据提取特征后进行主成分分析(principal component analysis，PCA)的方法[12]对降噪效果进行判别，具体操作步骤如下。

首先对降噪后的数据进行特征提取，依据手持式电子鼻的采样方式和数据曲线的形状特点，选取响应差值Rr和一阶微分最大值Maxder为特征，其提取方法如下式所示：

(7)

Rr=max(St)-St0

(8)

式中：t为采样时间；St为传感器输出电压信号对应的数字量；St0为响应起始点对应的传感器输出电压信号的数字量。

然后使用PCA对特征矩阵进行分析，绘制PCA得到的前2个主成分PC1、PC2组成PCA得分图，几种不同降噪方法得到的PCA得分图如图6所示。可以看出，几种降噪方法对于茅台、国窖以及西凤酒的区分效果比较好，体现在图中即为这3种酒样本和其他酒的区分度比较高；软、硬阈值函数降噪对于汾酒、五粮液、剑南春这3种白酒的区分程度较差，3类样本群在图中较为混乱，没有明显的边界；而改进的阈值函数降噪和中值滤波加SG滤波降噪对于这3种白酒的区分程度稍好，3类样本群在图中虽有重叠部分，但是重叠部分的面积相对较小。可以看出，软、硬阈值降噪的方法有一定的缺陷，不利于不同种类白酒的分类。

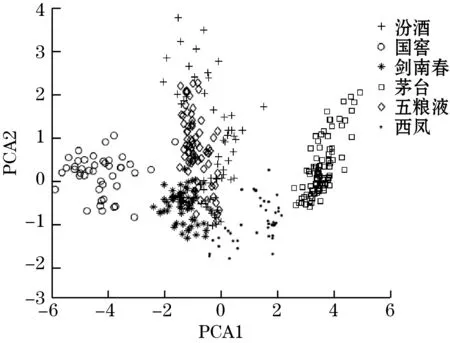
(a)软阈值函数

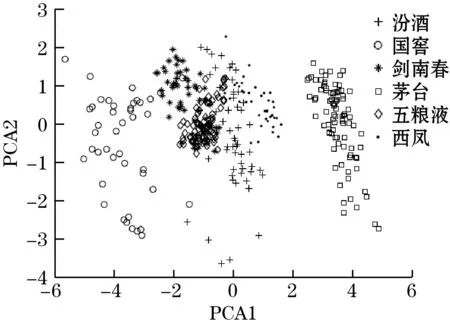
(b)硬阈值函数

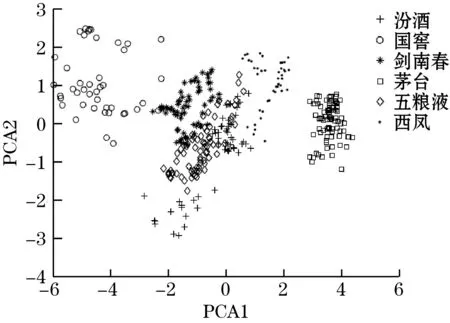
(c)改进的阈值函数

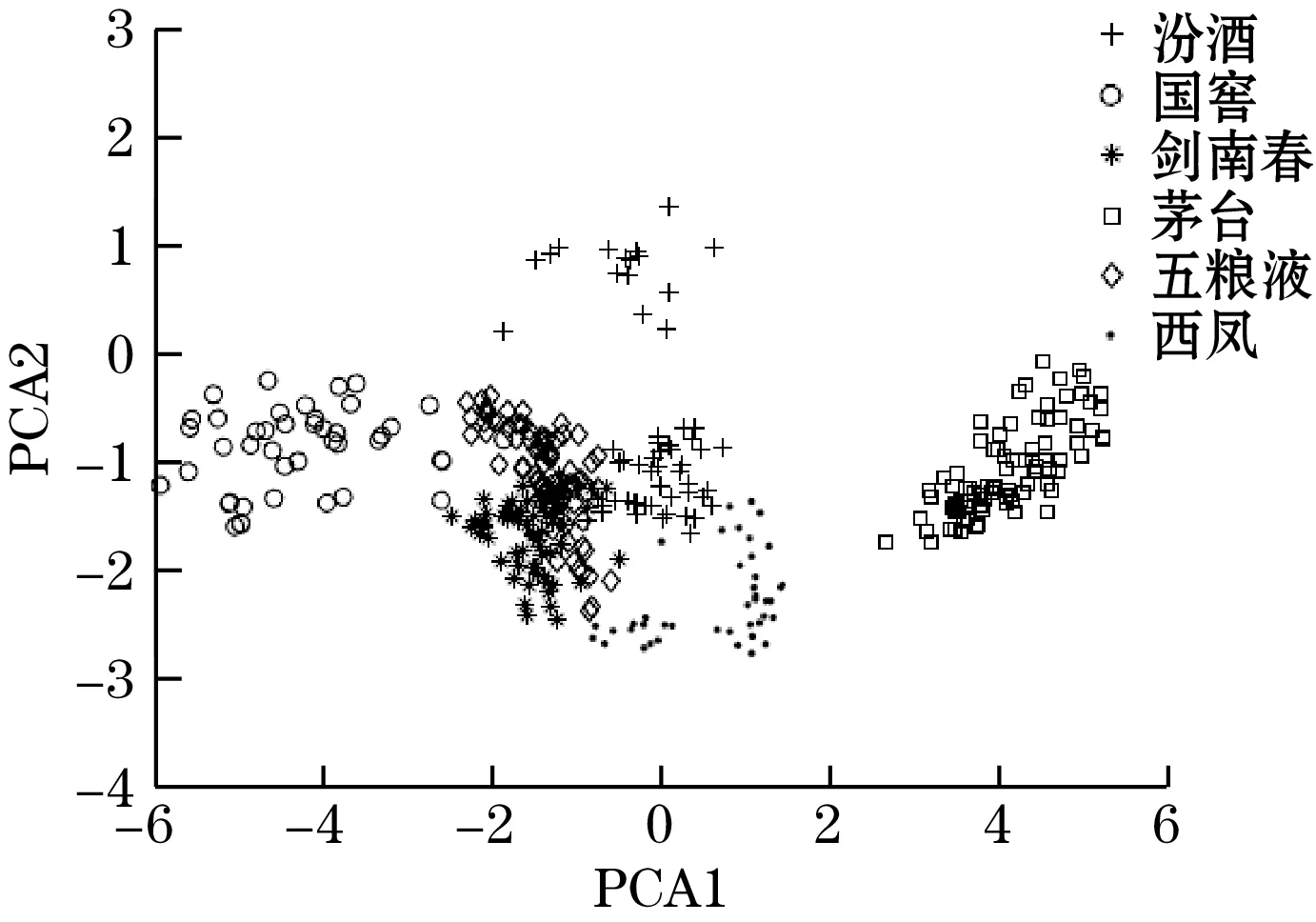
(d)中值滤波加SG滤波图6 不同滤波方法的PCA得分图

为了定量地描述不同降维方法的分类性能，本文引入了样本特征的类间离散度Sb和类内离散度Sw[20]，其中Sb可以表示不同类别样本之间的分离程度，Sw代表同一类别的样本的分离程度，其定义如下：

(9)

(10)

式中：c为样本类别数；ni为第i类样本的样本数；Mi为第i类样本的均值；M为所有样本的均值；Xij是第i类的第j个样本的特征。

不同的降噪方法对应的类间、类内离散度以及二者比值如表3所示，从分类的角度来看，类间离散度应该越大越好，而类内离散度应该越小越好，这样有利于后续的模式识别，故比值越大的降噪方法对分类更为有利，从表3可以看出，改进的阈值函数降噪方法降噪后的类间离散度最大，说明其对不同类别的样本区分程度较好，其类内离散度和软阈值函数相近，且小于硬阈值函数，说明软阈值函数和改进的阈值函数降噪对相同类别的样本聚类的效果好。中值滤波加SG滤波降噪的类内离散度最低，但是类间离散度较低，说明该降噪方法对于同类别的样本的聚类效果较好，但是不同类别样本之间的区分程度较差。从Sb与Sw的比值来看，改进的阈值函数降噪的效果最好，中值滤波加SG滤波降噪方法次之。

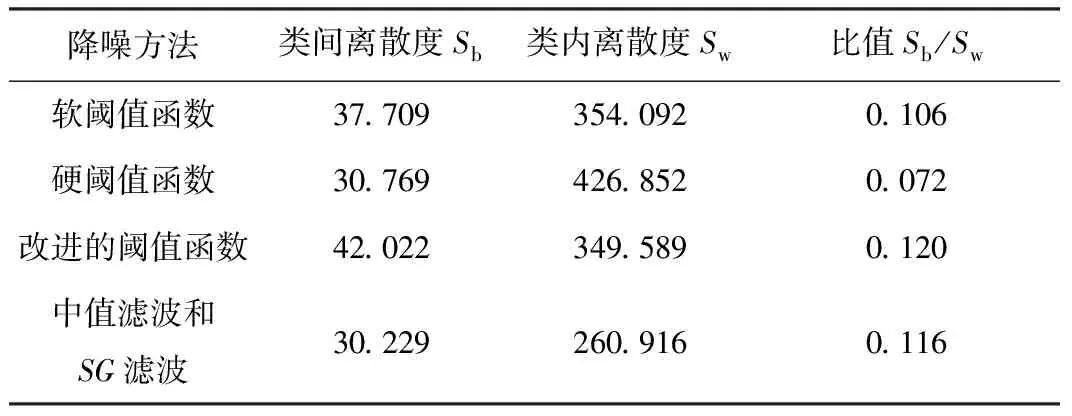
表3 不同降噪方法对应的类间、类内离散度及其比值

5 结束语

为了去除白酒电子鼻检测信号中存在的噪声，本文在软、硬阈值函数小波降噪方法的基础上提出了一种改进的小波阈值函数，使之同时具备了软、硬阈值函数的优点，并且其降噪的效果可以通过调整尺度因子进行微调。通过仿真验证可知，改进的阈值函数小波降噪算法可以在不损失有效信号的同时对噪声进行有效地过滤，相比软、硬阈值函数小波降噪方法，改进的阈值函数小波降噪方法降噪后得到的SNR更高，RMSE更低，降噪效果更好。将改进的阈值函数降噪方法应用到白酒电子鼻的实验数据中，结果表明，相比软、硬阈值函数小波降噪方法以及中值滤波加SG滤波降噪方法，改进的阈值函数小波降噪方法对于数据有较好的降噪效果，且降噪之后的数据集有着较大的类间离散度和较小的类内离散度，利于不同类别的白酒之间的分类。以上仿真和实验结果可以说明，改进的阈值函数有效地克服了软、硬阈值函数的缺点，且可以有效减少电子鼻中的噪声，为电子鼻数据的降噪处理提供了一种可行的思路和方法。