基础实验试题C：迈克耳孙干涉仪及其应用

廖 怡，秦 珠，冯列峰，王永祥，蒋学慧,许宝忠

(天津大学 a.理学院 应用物理系,天津 300354;b.精密仪器与光电子工程学院，天津 300072)

干涉是最基本的波动光学现象之一，在大学基础物理实验中，迈克耳孙干涉仪的调节与使用是光学实验的重要组成部分. 第7届全国大学生物理实验竞赛基础实验试题C，从产生干涉条纹现象的基本原理出发，考查学生调节迈克耳孙干涉仪的动手能力，根据所提供的实验仪器判断并选择合适的光源实现对空气折射率和透明薄玻璃片厚度的测量. 前2道试题均为基础光学实验内容，试题3为拓展测量内容，旨在考查学生充分理解白光干涉特点的基础上，采用补偿的方法完成测量,要求学生利用3个几何尺寸相同的液体槽和已知质量分数的液体，测量待测液体的质量分数. 全部试题要求学生设计完善光路、推证测量公式并进行测量操作，试题比较全面地考查了学生对迈克耳孙干涉仪干涉光路的理解及运用.

1 实验原理

迈克耳孙干涉仪利用分振幅法产生双光束以实现干涉，通过调整全反射镜，可产生等倾干涉条纹，也可产生等厚干涉条纹，利用干涉条纹的变化可以测量基本光学参量.

图1为迈克耳孙干涉光路图，干涉仪主要由4面高品质的光学镜片和1套精密的机械传动系统组成，其中作为分束器的G1是镀有半透膜的平行平面玻璃板，与相互垂直的平面反射镜M1和M2各成45°，使光束一半反射一半透射，又分别被反射镜反射返回分束器会合，射向观察位置E. 补偿板G2(平行于G1)，是与G1的厚度和折射率都相同的平行平面玻璃板，它用于补偿光束Ⅱ在分束器G1中少走的光程，使得2路光的光程差与经过玻璃板的光程无关，而是由其他几何路程决定. 当反射镜M1和M2距分束器距离相等时，光路I和Ⅱ上任意波长光束的光程差近似为零，满足白光相干长度短的条件，于是白光也能产生干涉. M2固定，M1装在拖板上，转动手轮可通过精密丝杠带动拖板沿导轨前后移动. 当移动平面镜M1的位置时，干涉条纹的级次发生变化，从而实现某些物理量的测量[1].

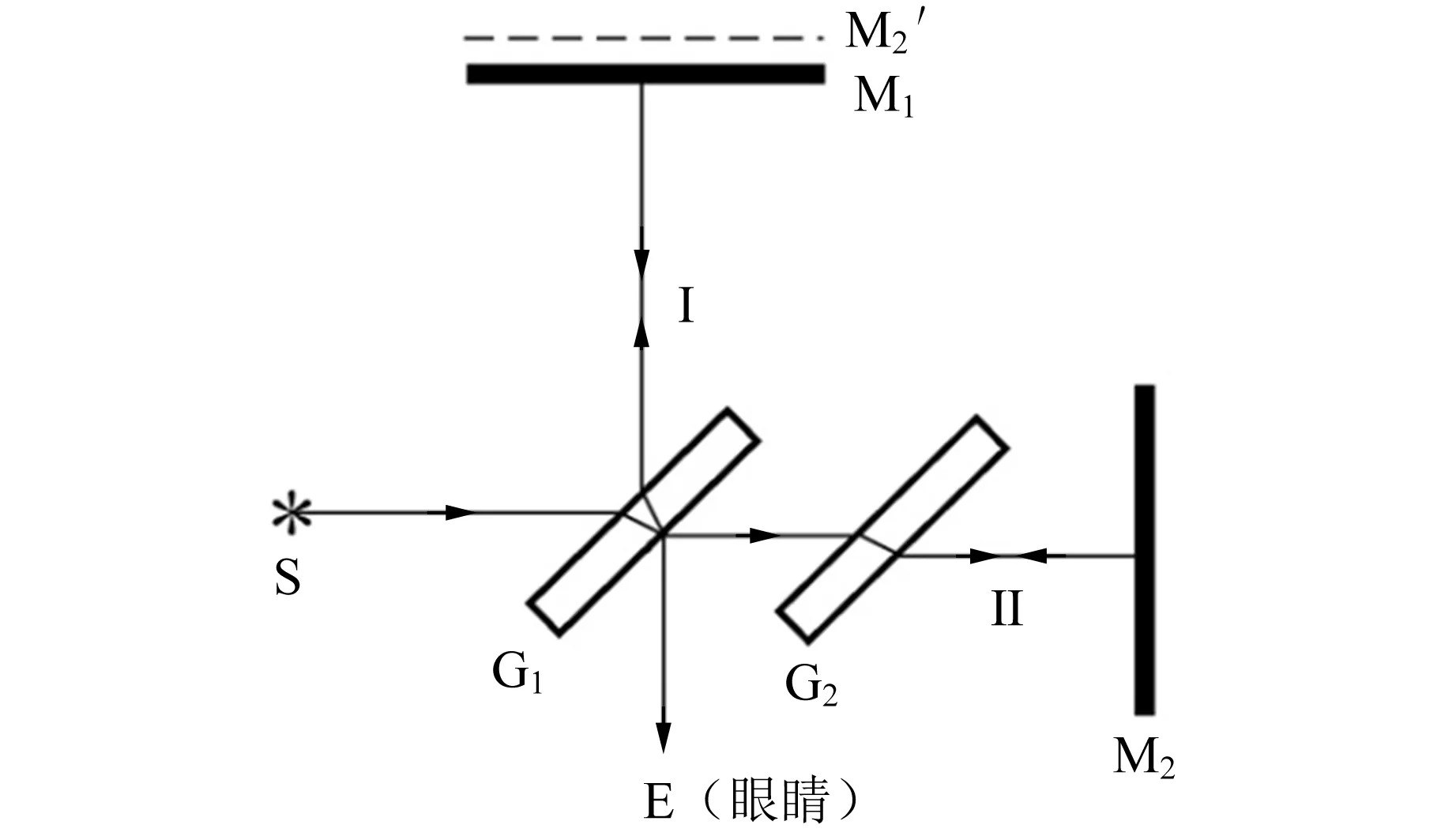
图1 迈克耳孙干涉仪光路图

2 实验器材

迈克耳孙干涉仪、He-Ne激光器(波长为632.8 nm)、钠光灯(波长为589.3 nm，带十字毛玻璃片)、白炽灯、扩束镜、待测薄玻璃片(折射率为1.516 3)、玻璃气室组件(长度为100.0 mm)、毛玻璃屏、纯净水(折射率为1.333 0)、未知质量分数的待测液体及液体槽(内宽为44.0 mm)等.

3 实验任务及解答

3.1 测量标准状态下空气折射率

根据提供的实验器材自行设计光路，测量标准状态(T0=273.15 K,p0=101 325 Pa)下的空气折射率n0.

3.1.1 实验要求

1)画出原理图，给出空气折射率n0的测量公式，写出推导过程.

2)记录实验测量数据，用图解法处理数据(要求测量4组数据)，计算标准状态下的空气折射率n0(要求保留小数点后5位)，室温为25 ℃.

3.1.2 试题解答

实验要求1)的空气折射率测量光路图如图2所示，在光路I(或者光路Ⅱ)中放入玻璃气室组件，如果气室内空气的压强改变Δp， 相应折射率改变Δn，则干涉光路将增加光程差δ，从而引起N个干涉环的变化.设气室内空气柱的长度为l，则有

图2 空气折射率的测量光路图

δ=2Δnl=Nλ.

(1)

实验过程中不抽真空，而是采取打气的方法增加气室内的粒子数量，根据气体折射率的改变量与单位体积内粒子数的改变量成正比的规律，求出标准状态下的空气折射率.对有确定成分的干燥空气来说，单位体积内的粒子数与密度ρ成正比，即

(2)

式中，ρ0是空气在标准状态下的密度，n和ρ是对应于任意温度T和压强p下的折射率和密度.

由理想气体状态方程，有

(3)

如果实验时温度T不变，由压强的变化所引起的折射率n的变化为

(4)

考虑T=T0(1+αt)(其中α为相对压力系数，α=1/273.15=3.661×10-3℃-1，t为摄氏温度，即室温)，代入式(4)有

(5)

将式(1)代入式(5)得到标准大气压下

(6)

实验要求2)现象解释：玻璃气室总长度大于100 mm，应放置在光路I中.利用气压计向气室内打气到某一气压值p，再缓慢放气至没有条纹吞吐变化为止，此时，气压计示数为零，记录气室内压强的改变量Δp及所对应的干涉条纹变化数N，做N-Δp关系图，代入式(6)求得标准状态下的空气折射率n0(数据详解及作图略).

此处要求学生选择实验所用光源，实验提供了激光和钠光，理论上任意光源均可完成该实验，但从实际的干涉现象来看，若选择钠光作为光源：其一，此时光路Ⅰ中放入了较长的玻璃气室，从而使其与光路Ⅱ的光程差较大，会导致所得到的钠光等倾圆环很小且密集，反衬度较差；其二，由于钠光源的双线结构特点，干涉条纹反衬度周期性起伏，造成放气过程中引起的光程差变化的同时出现条纹反衬度为零的现象，使得测量过程中不容易记录圆心处的圆环吞吐，影响记录条纹变化数. 若选择He-Ne激光作为光源，激光经过扩束镜后形成点光源的干涉，用光屏接收非定域干涉条纹，更容易完成测量.

3.2 测量平板薄玻璃片的厚度

根据提供的实验器材设计光路，利用迈克耳孙干涉仪完成平板薄玻璃片(折射率为1.516 3)厚度D的测量.

3.2.1 实验要求

1)简述实验方案，推导薄玻璃片厚度D的理论表达式，给出推导过程.

2)记录实验数据，并进行数据处理，不要求计算不确定度.

3.2.2 试题解答

实验要求1)简述实验方案：由于本题在光路中放置薄玻璃片前后，所见到的干涉条纹呈阶跃式变化，因此不能采用记录条纹数的方法，而采用“零光程差”法，即白光相干长度短(波长数量级)，仅当干涉仪两臂的光程差近似为零时才能出现干涉条纹.先调节出空气中零光程差时的白光干涉条纹，在光路Ⅰ(或光路Ⅱ)中插入待测薄玻璃片后，由于光程差变化，通过移动动镜M1补偿由于光路中插入薄玻璃片而附加的光程,再次找到零光程差的位置，记录M1在插入薄玻璃片前后2次出现白光干涉条纹的位置M1和M1′，即可测量薄玻璃片的厚度[2-7].

公式推证：如果光路中折射率发生变化，光程差为

δ=2(n1-n0)D,

(7)

式中n1和n0为玻璃和空气的折射率.动镜M1移动|M1―M1′|，光程差为

δ=2|M1-M1′|,

(8)

则薄玻璃片厚度为

(9)

实验要求2)现象解释：数据测量的关键在于调节出2次白光的彩色干涉条纹，并且分别记录动镜M1移动前后的位置.要完成测量可以通过眼睛直接观察和在屏上观察干涉条纹2种方式.实验提供的白光为白炽灯，是扩展光源，相应的辅助调节的光源也要使用扩展光源，2个光源同时照射到干涉仪上，用眼睛观察干涉条纹，并根据白光干涉现象确定零光程差的位置，避免盲目调节.所提供的实验仪器限定了只能用带有十字毛玻璃片的钠光源作为辅助光源.如果使用激光，经过扩束后也可以在屏上得到点光源干涉条纹，此时需要借助透镜使白光干涉条纹呈现在屏上，而实验并没有提供透镜，因此，题目2选择用钠光和白光来完成测量即可.调节中注意消除仪器回程误差(调节方法略)，计算时，n0取第一部分实验结果(或近似取值n0=1.000 0)，以1组数据为例，M1=122.201 88 mm，M1′=121.596 63 mm，动镜移动的距离|M1―M1′|=0.605 25 mm，已知薄玻璃片折射率n1=1.516 3，根据式(9)计算得到薄玻璃片厚度D=1.172 3 mm.

3.3 测定液体的质量分数

待测溶液的折射率[8-11]与质量分数之间满足线性关系n2=ac+b,其中a=0.22，b=1.326 7，即n2=0.22c+1.326 7.结合实验器材，利用迈克耳孙干涉仪测定待测液体的质量分数.

3.3.1 实验要求

1)简述实验方案，并说明如何消除回程误差，并画出原理图.

可以申请提示卡C-1，申请后直接扣除分值20分.

2)推证待测液体质量分数的公式，写出推导公式.

3)记录实验数据，并进行数据处理，得到待测液体的质量分数，不要求计算不确定度.

3.3.2 试题解答

实验要求1)的原理图如图3所示.

图3 液体质量分数的测量光路图

简述实验方案：本小题所用到的原理，在3.2的基础上稍加拓展，如果直接在其中1支光路中放入盛有液体的玻璃槽，则附加的光程差远远大于白光的相干长度，即使移动动镜M1也观察不到白光的干涉条纹，此时需要采用“补偿”法，具体分2步完成测量. 首先，同时将盛有纯净水的2个液体槽分别放入光路Ⅰ和光路Ⅱ中,调节出白光干涉条纹，记录此时动镜的位置M1. 然后，将光路Ⅰ中的纯净水更换为待测液体，由于光程差发生变化(液体质量分数变化引起的)，白光干涉条纹消失. 调节动镜M1向分束器G1方向移近，再次找到零光程差的位置，即出现清晰的彩色条纹，记录动镜的位置M1′.

光源的选择详见题目2，调节中注意消除仪器回程误差(调节方法略).

实验要求2)公式推证：待测溶液的折射率与质量分数之间满足

n2=0.22c+1.326 7,

(10)

对于折射率分别为n21和n22的2种液体，光程差改变量为

dδ=2L(n22-n21),

(11)

其中L为液体宽度.

2次出现白光干涉条纹，动镜M1移动的距离为|M1―M1′|，光程差变化

dδ=2|M1-M1′|,

(12)

合并整理式(10)～(12),已知水的折射率为1.333 0，待测液体质量分数为

(13)

实验要求3)中提供的待测液体是质量分数为22.00%的NaCl溶液，记录数据并计算待测液体质量分数，此处以1组仪器测量结果作为参考，M1=122.508 82 mm，M1′=120.657 95 mm，因此动镜移动的距离|M1―M1′|=1.850 87 mm，待测液体的质量分数为21.98%.

4 考试结果及评析

基础实验试题C分为3道题目，总分100分，其中题目1和题目2分别占30分和20分，题目3占50分. 原理解释(光路图)和推导公式占27分，实验设计占20分，测量(光路调节和数据记录)以及数据处理占53分. 共有51人参加考试，其中8人陆续申请了提示卡. 总分得分分布如图4所示，具体各小题得分情况如图5～7所示.

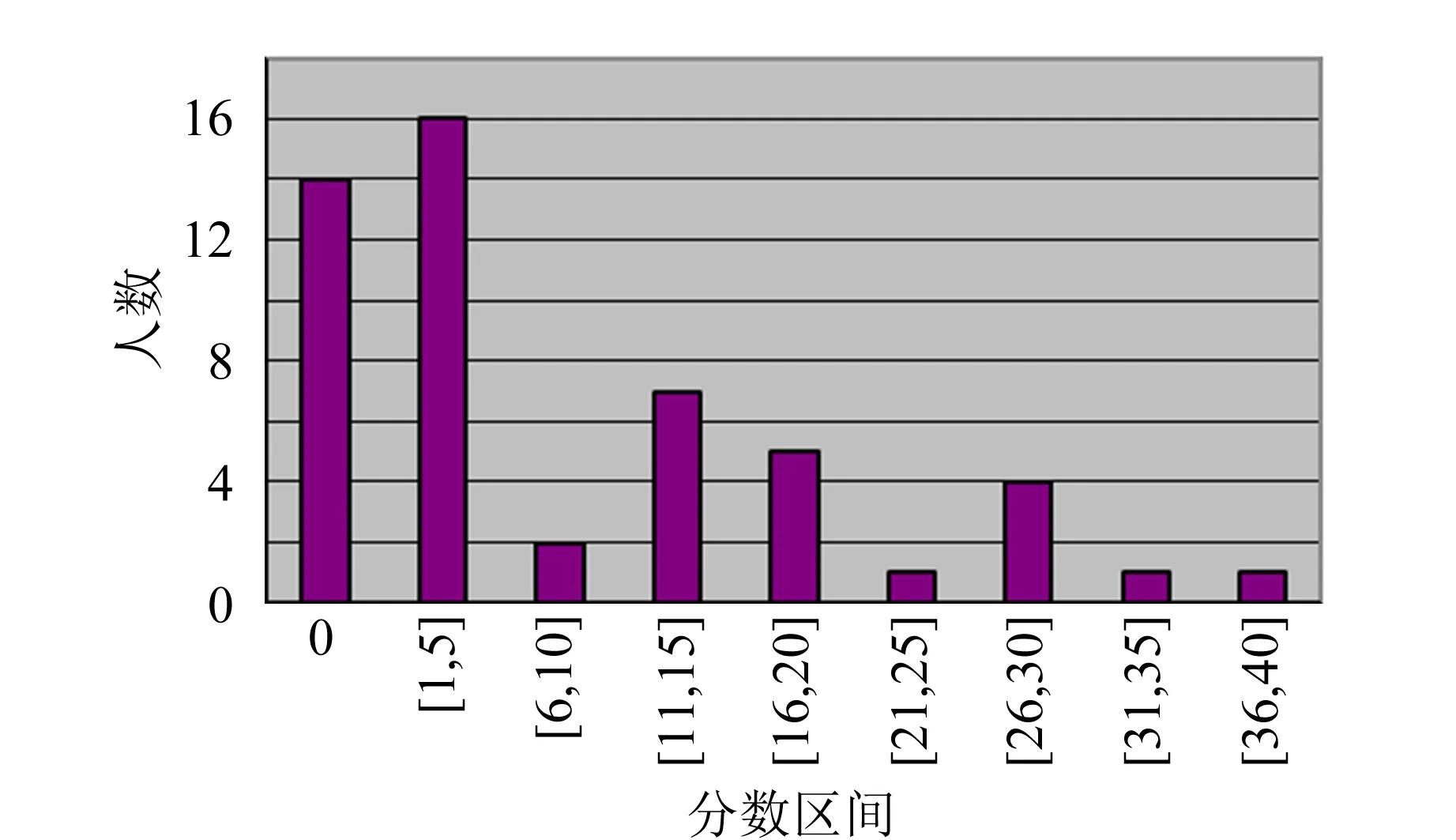
图4 总分分布图

(a)第1问

题目1和题目2均包括2个小问：简述实验方案和测量数据，实验内容和数据处理难度适中. 前2道题目分别使用2种光源完成测量，考查学生对迈克耳孙干涉仪光路的了解程度，以及对点光源和扩展光源所产生的干涉现象的理解. 题目3包括3个小问，是整套试卷的难点部分，其中第1个小问可以借助提示卡得到实验光路图、实验方案设计和操作步骤简述，代价是直接扣除20分. 题目3是题目2的拓展，对考生掌握白光干涉的理论知识和光路调节能力都有较高的要求.

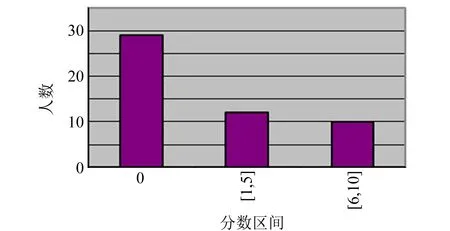
(a)第1问

(a)第1问

从实验过程和答卷结果看，在理论推导方面，前面2道基础题，大部分考生能画出原理图并完成公式推导. 题目3中申请提示卡的考生，在简述实验方案和原理图时目的比较明确，但扣除20分后，得分率也不高. 在测量环节，只有很少一部分考生给出正确的测量结果. 本实验没有要求学生自组迈克耳孙干涉光路，而是提供了迈克耳孙干涉仪，命题组在出题阶段曾考虑让学生自己动手调节分束器G1、补偿板G2、平面镜M1的平行度，会占用20～25 min，考虑到整体命题难度，将此部分提前预调节好.

本次竞赛考核结果反映出考生基本掌握干涉的基础知识，但是对基础知识迁移和拓展的能力较弱，有相当一部分考生的基本光学仪器调节能力差. 这提示教师在实验教学中不能只注重数据结果，而忽视掌握仪器结构及调节方法，应加强引导学生结合实验仪器，运用基础物理知识解决实际问题. 希望本文能够为后续的大学物理实验竞赛以及大学物理实验教学提供参考.