转动惯量对负载音叉固有频率的影响
2021-11-29张阅剑刘珂溦白在桥
张阅剑,刘 悦,刘珂溦,白在桥
(北京师范大学 物理学系,北京 100875)
音叉的受迫振动是大学物理基础实验[1-8],此实验的基本内容是测量音叉在不同负载下的固有频率. 理论分析时,通常将音叉等效为弹簧振子,负载等效为附加质量. 这样音叉固有周期的平方就与负载质量呈线性关系,而等效劲度系数k与固定负载的位置有关[1-3]. 在实验中发现,虽然该模型可以描述共振频率对负载质量的依赖关系,但仍存在细微的不足. 按照弹簧振子模型,在固定的位置加负载,音叉的固有频率仅与负载的总质量有关,而与加载负载的质量分布无关. 而实验结果表明,负载的质量分布改变也会导致固有频率发生轻微的改变,例如图1所示的2种不同负载分布构型.
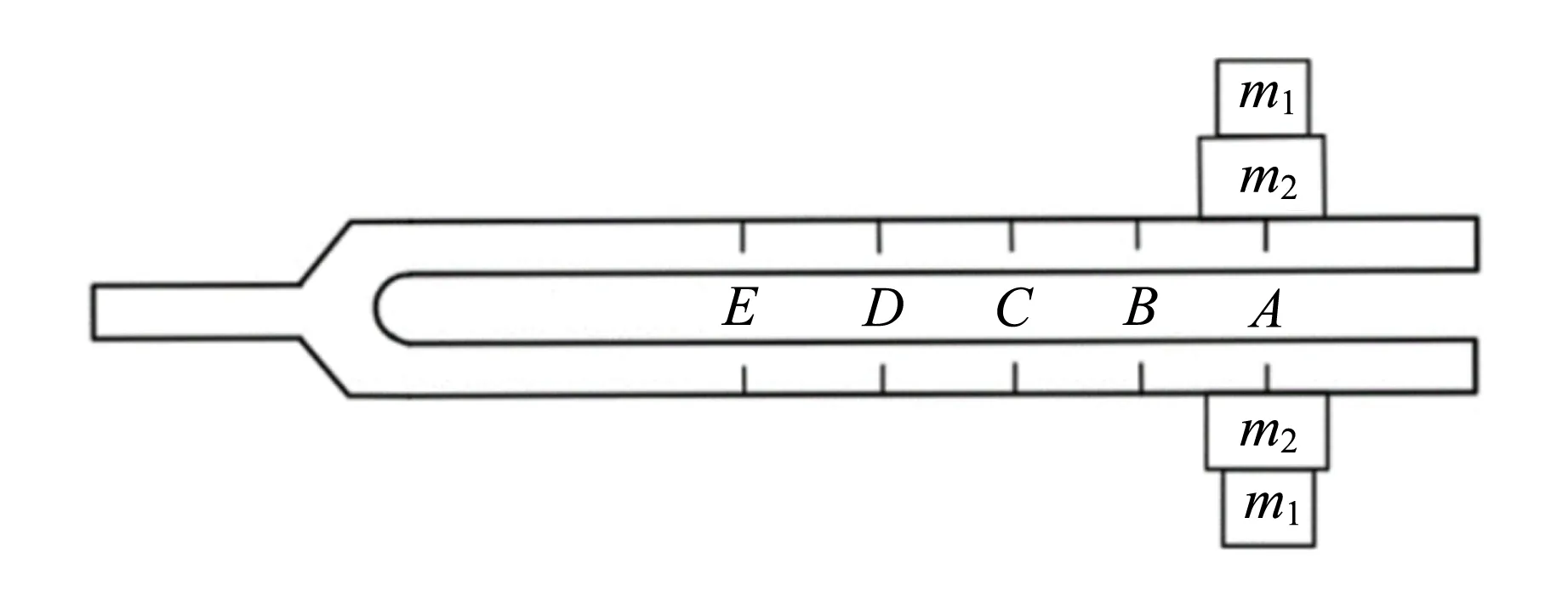
(a)
虽然负载的总质量都为2(m1+m2),但图1(b)的固有频率要比图1(a)的低0.8 Hz左右. 相比加负载引起的几十Hz固有频率偏移,此差异很小,但它远大于固有频率测量的不确定度,此现象存在的物理机制值得深入研究.
1 理论分析
音叉可看成无穷多个小质元,它们之间通过弹性耦合构成弹性连续体. 当振动幅度较小时,可以认为弹性作用服从胡克定律,依照维里定理,音叉的动能和势能的平均值相等.
设基频振动的位移为
φ0(x,t)=aΦ0(x)cos (ω0t),
(1)
式中,x为空间坐标,ω0和Φ0(x)分别为基频的角频率与振动模式,a为模振幅.音叉基频简正模的平均动能为
(2)
弹性平均势能为
(3)

(4)
如果在音叉上增加负载,新系统的简正模和对应的本征频率发生变化.若所加负载质量较小,可以用微扰论来计算.如果只做ω2一阶微扰修正,只需在未受微扰的简正模Φ0(x),即由
φ(x,t)=aΦ0(x)cos (ωt)
(5)
描述振动的基础上计算动能和势能平均值.因为简正模没有变,等效劲度系数也不会变,平均弹性势能仍由式(3)给出.但因频率变化,音叉的平均动能变为
(6)
设负载被加在固定点x0,负载的平动方程为
z(t)=aΦ0(x0)cos (ωt)≡aβcos (ωt).
(7)
此外,负载还存在轻微的转动,转动角度为
(8)
因此负载的平均动能为
(9)
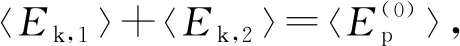
(10)
需要指出的是,作为一阶微扰,此式(10)理论上只适合负载质量较小,基频振动模式基本不变的情况.至于其实际的效果,需要用实测数据检验.
2 装置与方法
本文使用DH4615型音叉受迫振动与共振实验仪进行实验. 为记录波形,实验使用了数字示波器(RTB2002),实验装置照片参见图2.

图2 实验装置
测量音叉固有频率有2种常用方法:共振法和暂态法. 由于需要测量多种情况下的固有频率,因此采用测量速度更快的暂态法. 用橡胶锤敲击音叉,使其做阻尼振动,用示波器记录通过感应线圈得到的衰减振动曲线,如图3所示. 示波器的采样率为5.45 kHz,波形长度为24 s,包含1.3×105个数据点.
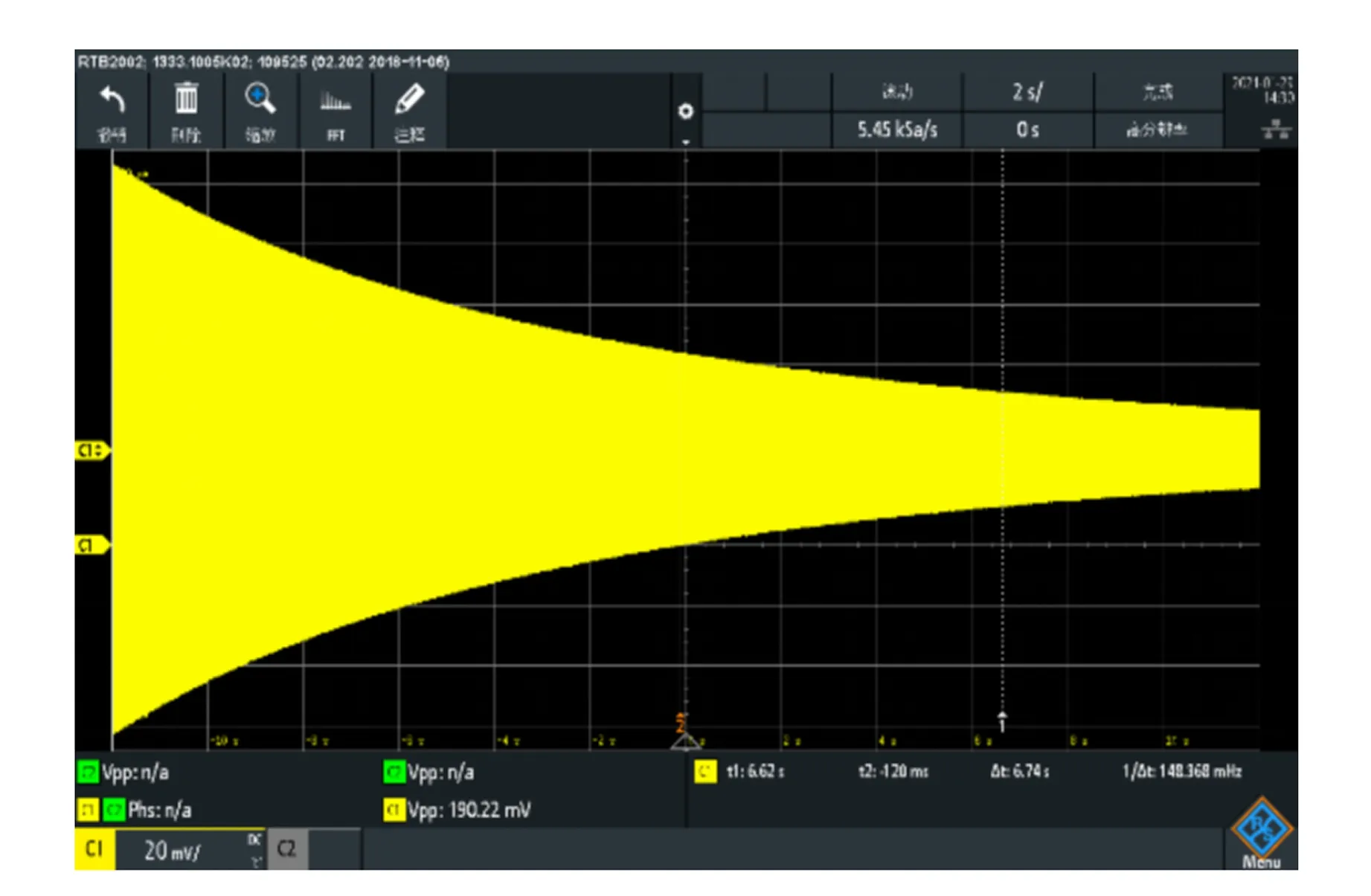
图3 音叉振动输出信号
将波形数据导入Matlab处理. 把数据分割成65段波形(每段含2 000个数据),每段波形都可以很好地拟合为正弦函数,因而可得到65个随时间变化的振幅与频率. 振幅随时间的变化如图4所示,可以用指数衰减a(t)=Ae-δ t很好地拟合. 画出频率与振幅的关系(图5),可以看出频率存在随振幅减小而增大的趋势,这种趋势体现了振动的非线性. 由于频率变化范围不超过0.01 Hz,因此非线性效应并不显著. 利用二次函数f=f0+c1a+c2a2拟合频率-振幅曲线,所得f0为振幅无限小的振动频率. 理论上,阻尼振动的频率要略低于固有频率,由于这2个频率都不大于0.2 s-1,比频率小3个数量级,固有频率的修正都在0.001 Hz以下,因此f0可直接作为音叉的固有频率. 相同情况下多次测量,所得f0一般在0.01 Hz位上略有区别,据此单次f0的测量不确定度在0.01 Hz量级.
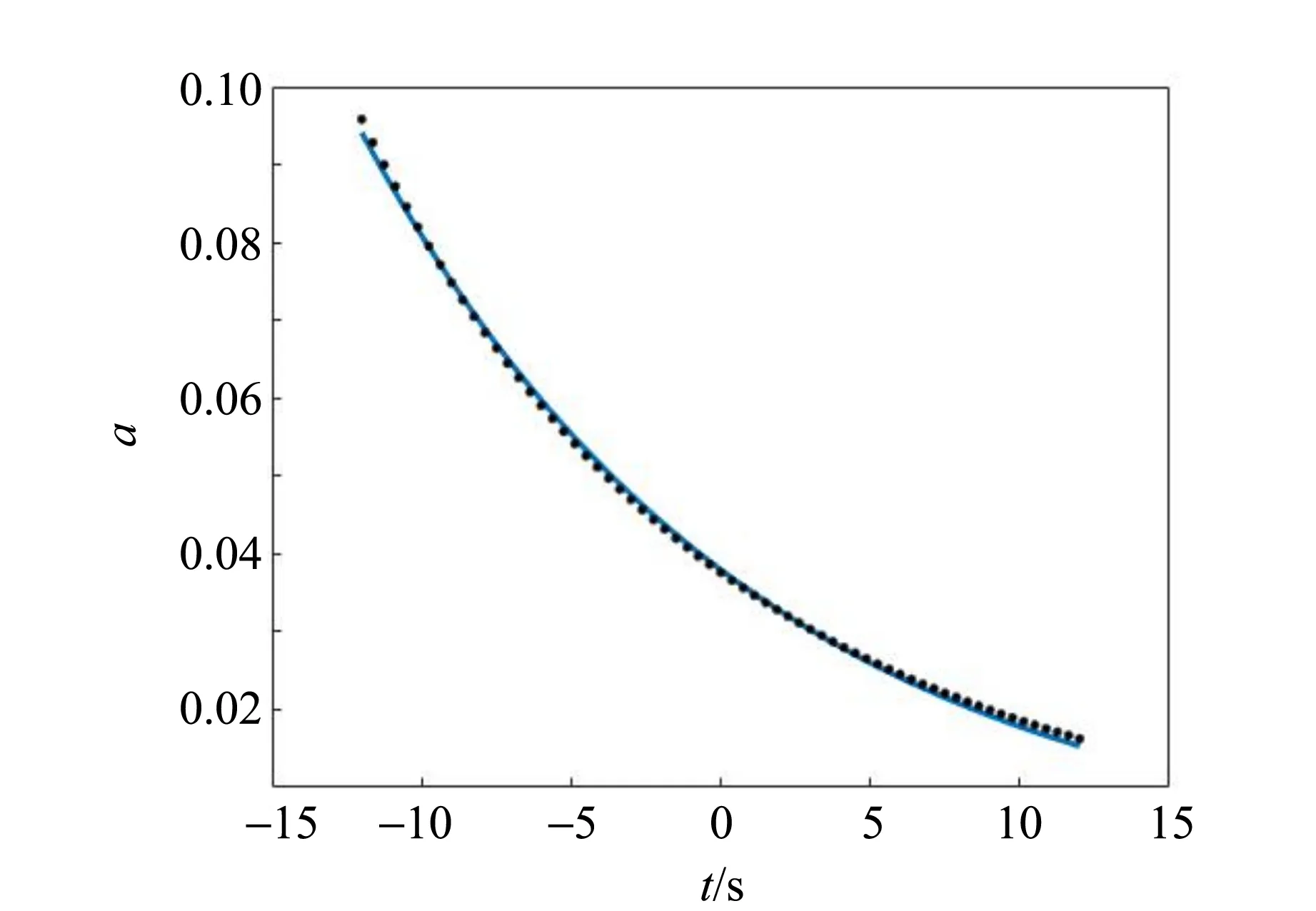
图4 阻尼振动的振幅衰减曲线
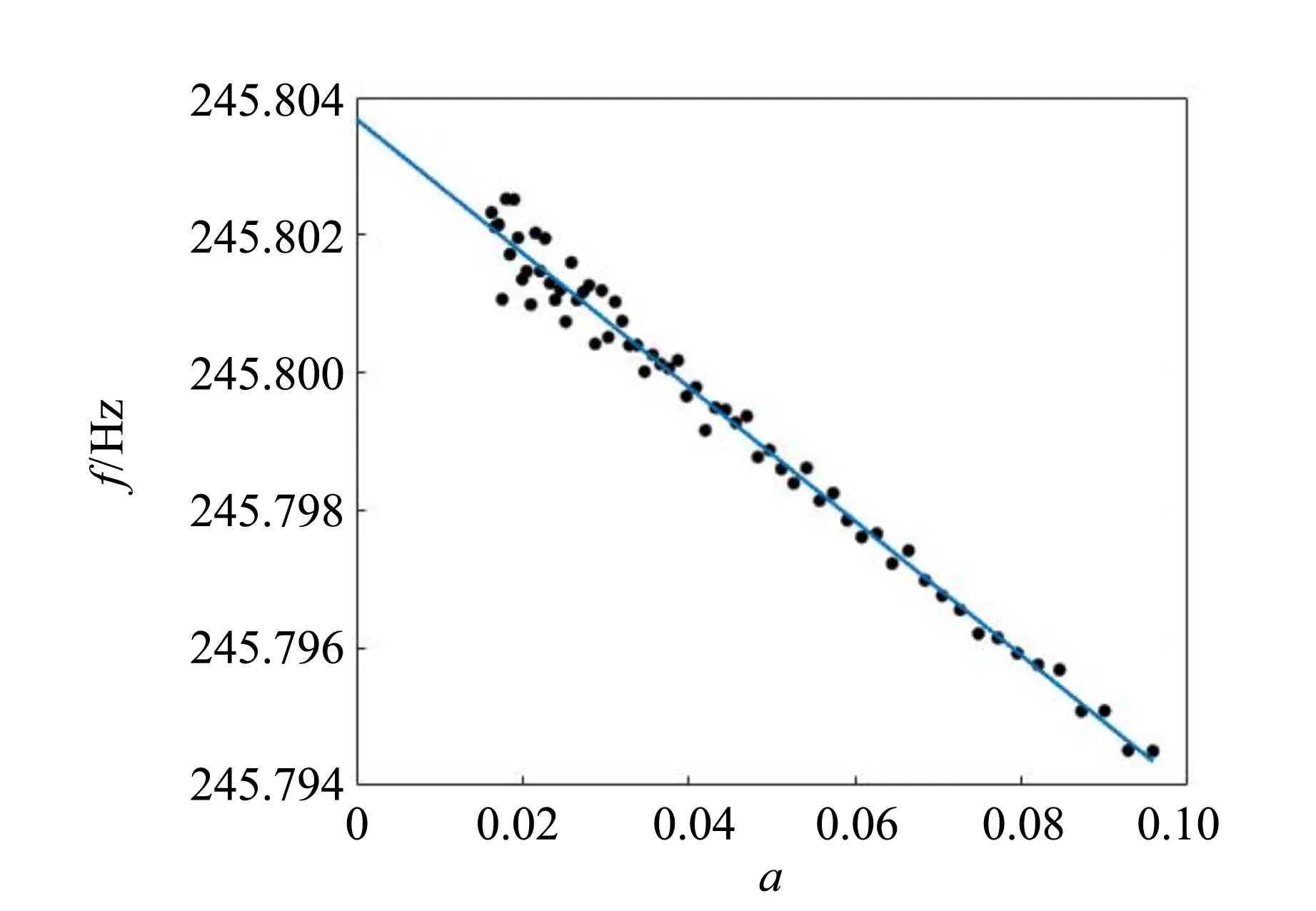
图5 衰减法测量固有频率
实验使用大、中、小3种圆柱形砝码,具体参量见表1. 使用3种砝码的不同组合,按不同的叠放顺序固定在音叉的不同位置上. 音叉上有5个等间距分布的位置(记为A,B,C,D,E)可用于固定负载,它们到音叉自由端的距离分别为10,20,30,40,50 mm,音叉臂的长度为137 mm. 砝码中心有用于固定的螺孔,为简单起见,在计算转动惯量时将其简化为圆柱形. 因此砝码相对固定的转动轴(即砝码底面的中线)的转动惯量为
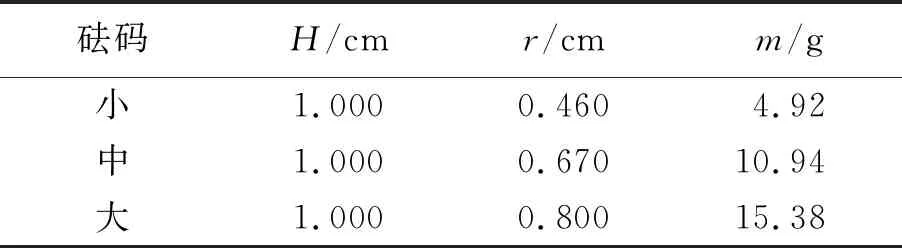
表1 不同型号砝码参量
(11)
2个砝码按图6(a)方式叠放,转动轴方向如图6(a)中虚线所示. 杆的振动与砝码旋转如图6(b)所示. 根据平行轴定理,总的转动惯量为
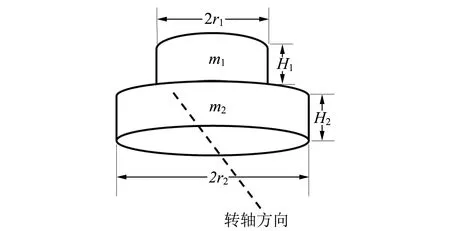
(a)两砝码叠放
Im1,m2=Im1+Im2+m1H2(H1+H2).
(12)
由于所有砝码的高度相同(都为H),可得
Im1,m2-Im2,m1=2(m1-m2)H2.
(13)
即较大的砝码在外侧时,转动惯量较大.
3 实验结果
表2列出了用暂态法测得不同质量的砝码组合固定在音叉不同位置时的固有频率. 第1列中按照从上向下的顺序中标出了砝码的放置顺序,其中“|”区分了音叉的2个臂. 例如图1(a)所示组合顺序,被表示为“小中|中小”. 表中的每个固有频率为2次测量的平均值.
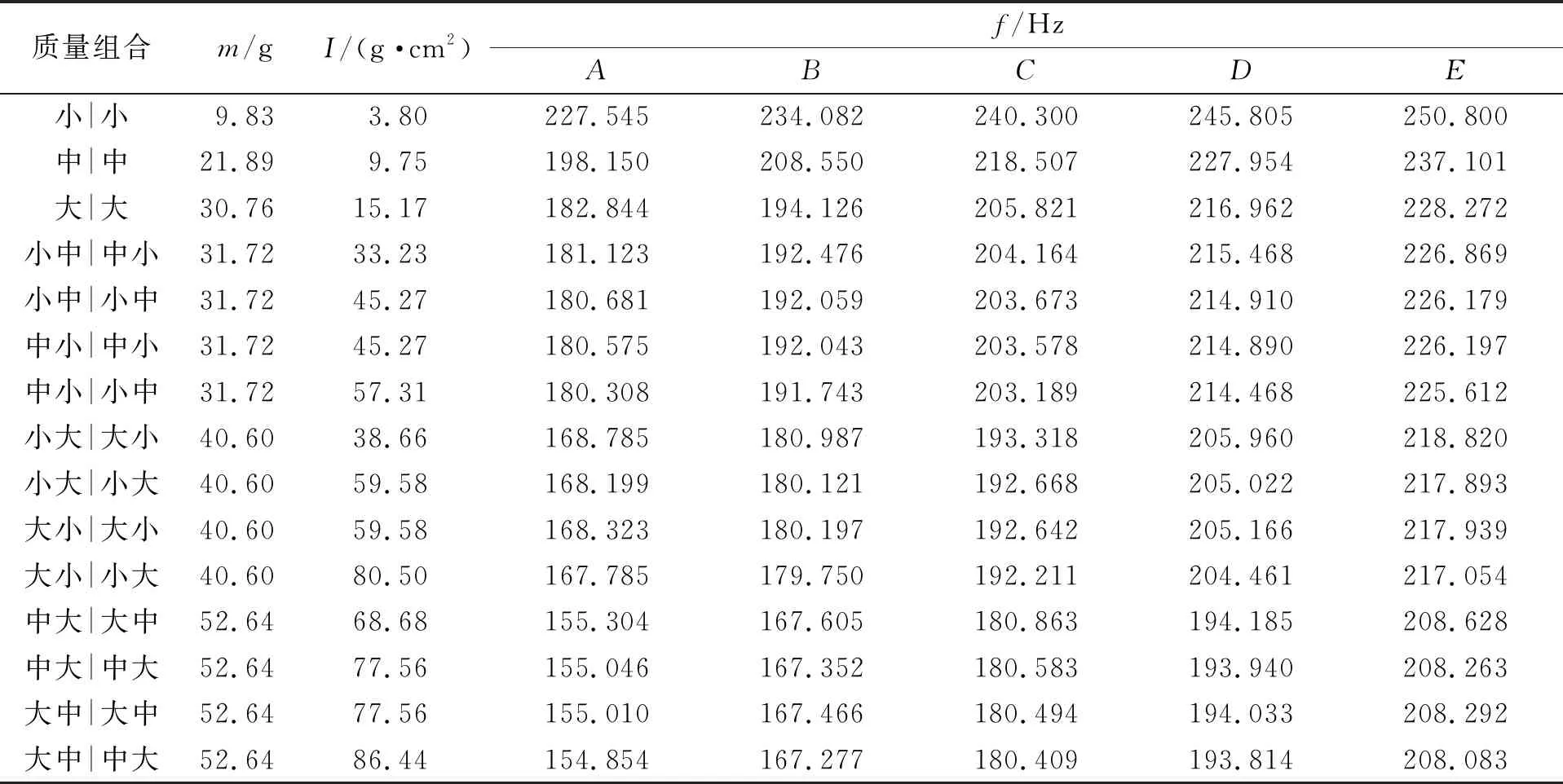
表2 不同质量组合方式对应的固有频率
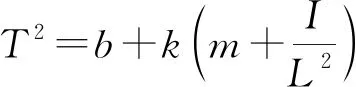
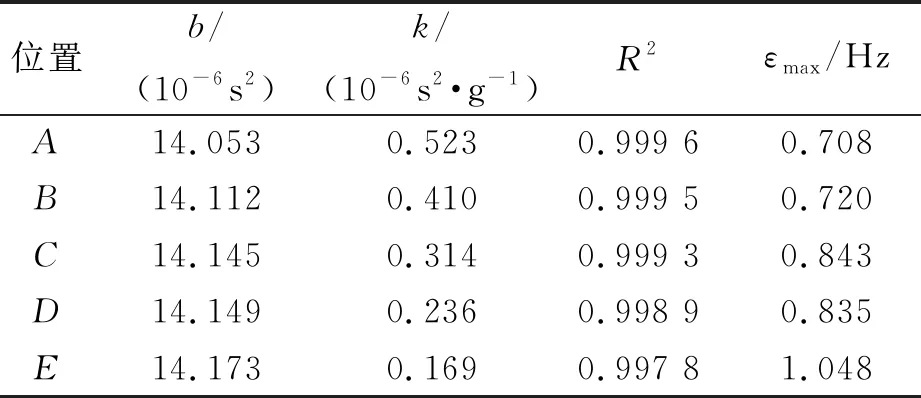
表4 负载固有频率的拟合结果(T2=b+km)
显然,考虑到转动惯量后的改进模型可以更好地描述实测数据.首先改进模型的相关R2比简化模型更接近1.由于1-R2正比于拟合残差的平方和,因此改进模型可使拟合残差的平方降低1个数量级.其次可以比较固有频率的拟合值与测量值的最大误差,结果用εmax表示.可以看出考虑到转动惯量后,εmax会降低一半.当固定位置从A向E移动时,L逐渐变小,转动惯量的影响逐渐增大.与之对应的是,无论从R2还是从εmax的角度看,简化模型的拟合情况都会逐渐变差,而改进模型并没有这个趋势.
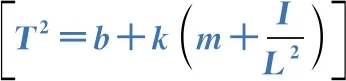
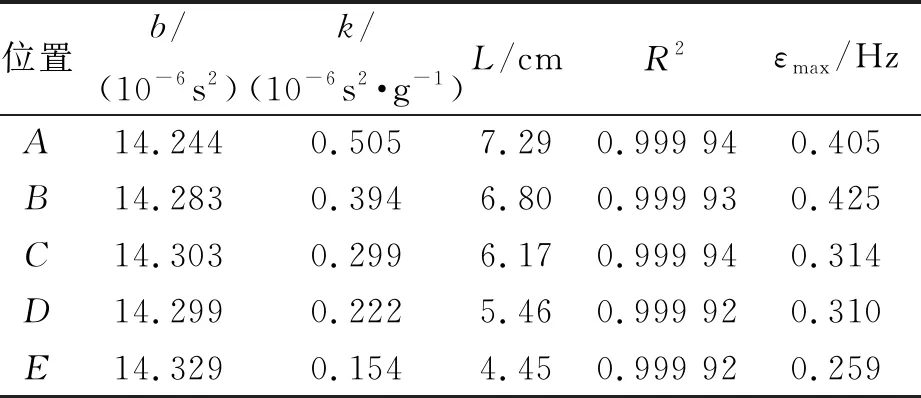
位置b/(10-6s2)k/(10-6s2·g-1)L/cmR2εmax/HzA14.2440.5057.290.999 940.405B14.2830.3946.800.999 930.425C14.3030.2996.170.999 940.314D14.2990.2225.460.999 920.310E14.3290.1544.450.999 920.259


图7 固有周期平方T2与负载等效质量m*的关系
4 讨 论
针对负载音叉弹簧振子模型不能解释的负载质量分布不同导致的固有频率差异问题,考虑负载的转动动能,得到了推广的负载音叉固有频率公式. 改进后的公式包含与负载转动惯量有关项. 经过与实测数据比较,改进后的公式更好地描述了负载音叉固有频率的变化规律.
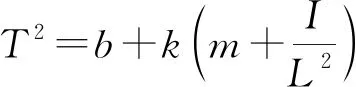
(14)
其中ξ0≈1.875 104是方程coshξcosξ=-1的最小正根,L0=137 mm为音叉臂长,而
(15)
在此近似下,音叉的基频模式的等效质量M和等效劲度系数K可分别表示为
(16)
(17)
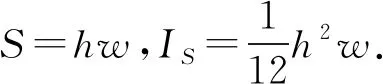
(18)
这样M=ρSL0就等于音叉臂本身的质量.音叉为铁质,ρ=7.8 g/cm3.实测h=0.55 cm,w=0.88 cm.因为m为负载的总质量,M也应该是2个音叉臂的总质量,即M=2ρhwL0=103 g.表5给出5个位置的k和L的估算值以及它们与拟合参量的比较.其中
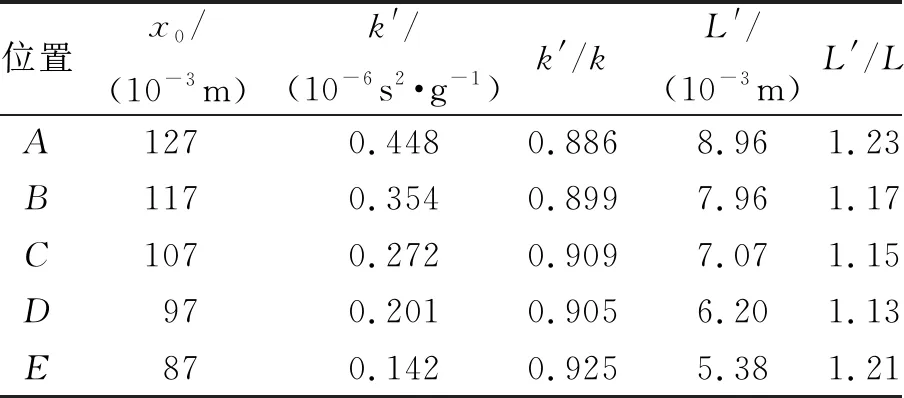
表5 拟合参量的理论估计
(19)
(20)
可以看出,估算值与拟合参量相差不大且变化趋势相同:k′比k小10%,L′比L大20%. 由于音叉的厚度并没有远小于其长度,欧拉-伯努利梁理论本身存在近似. 此外,音叉臂上的负载安装孔改变了音叉的质量和弹性分布,也会对简正模式产生影响. 综合上述因素,可以认为这种程度的符合有力地说明了本文理论模型的合理性.
