用真空杯改进混合法测量冰的熔化热实验

薛玉琪,何振辉

(中山大学 物理与天文学院，广东 珠海 519082)

冰的熔化热测量主要涉及温度测量和量热技术两大热学实验的基本问题. 量热学[1]以热力学第一定律(能量守恒定律)为理论基础，所研究的范围是如何计量物质系统随温度变化、相变、化学反应等过程中吸收或放出的热量. 量热学的常用实验方法有混合法[2]、稳流法[3]、冷却法[4]、电热法[5]等.

混合法是测量冰的熔化热实验的常用方法，但教学实践表明，用铝杯为量热器测量冰的熔化热，其精度一直较低. 即使采用了温度响应较快的热电偶以及计算机自动记录温度变化，增加了冰快速熔化过程中的温度数据点，但按原有方案所测量的冰熔化热仍然偏低，约20%. 分析原教学实验装置(DH4613)[6]，其铝杯量热器周围的隔热体因过于复杂且认为隔热效果足够好而没有被考虑在物理模型中，从而导致模型与实验对象不能对应. 随着工业化水平的提高，家用真空杯的保温能力可达到在数十分钟时间内，温度传感器读数不发生变化；此外，真空杯简单的结构有利于学生理论联系实际. 本文设计了用真空杯替代原铝杯及其隔热体的实验方案，并分析了实验误差的来源，经过1个学期，对学生实验结果进行统计分析和对比，并选择最优实验方案开展实验教学. 实验结果表明，采用真空杯作为量热装置，减小了热量散失对测量的影响，同时为学生测量量热器的热质量提供了研究空间，最终验证了把“冰的熔化热测量”作为居家实验的可行性.

1 理论基础

1.1 牛顿冷却定律

由牛顿冷却定律知[7]，当表面温度为T的物体在温度为Te的环境中自然冷却(T>Te)，单位时间该物体散失的热量与温度差成正比，即:

(1)

当物体温度T的变化是准静态过程时，认为温度充分均匀(表面温度与体温度一致)，根据能量守恒定律得:

(2)

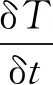
1.2 热平衡方程

在一定压强下，固体发生熔化时的温度称为熔化温度或熔点.单位质量的固态物质在熔点时完全熔化为同温度的液态物质所吸收的热量称为熔化热[8]，用L表示，单位为J/g.

将质量为m、温度为0 ℃的冰块置入量热器内，与质量为m0、温度为T0的水相混合，设量热器内系统达到热平衡时温度为T1.若忽略量热器与外界的热交换，即将水、冰和量热器看作是孤立系统，并假设量热器内筒温度总与水温相同，且内筒与外筒的漏热可以忽略.根据热平衡原理可知，冰块熔化成水升温吸收的热量与水和量热器内筒降温所放出的热量相等：

mL+mC0(T1-T′)=(m0C0+m1C1+M)(T0-T1)，

(3)

式中，T0，T1分别为投冰前、后水的近平衡温度，T′为冰的熔点(0 ℃)，C0=4.18 J/(g·℃)为水的比热，m1为量热器内筒的质量，C1为量热器内筒的比热；M为其他可能涉及的热质量.解式(3)得到冰的熔化热为

(4)

2 测量方案与物理模型

在传统实验教学中，冰的熔化热测量实验均采用量热器法，即式(4)所描述的物理模型，该模型忽略了漏热的影响，还将量热器与环境的关系理想化，如量热器及被测物体的温度同时均匀变化(热导无穷大)，将量热器与环境的关系简单化(只有1个环境温度). 被简化的物理模型不能反映真实的实验对象. 本文基于以上问题对传统实验方案进行改进，明确了实验装置与物理模型的对应关系，从而降低了实验的系统误差.

2.1 量热器法(铝杯+隔热体)

量热器法是基于原教学装置(DH4613)[6]及对应的方法. 量热器内胆为铝杯,比热为0.88 J/(g·℃)，隔热体包括广口保温瓶和用于支撑铝杯的亚克力盖(图1). 但隔热体在理论模型[式(4)]中是不存在的，其隐含的假设是隔热体本身也是环境之一. 系统中量热器的漏热较为明显(实验中量热器温度变化速率较快). 因此，需要采用外推法和冷热补偿法来修正漏热的影响[1]，但是会遇到如下问题：环境温度如何定义，是隔热体外的实验室温度，还是隔热体与铝杯之间的空气的温度，或者是支撑铝杯的亚克力盖子的温度. 本文通过多次测试，发现即便采用自动准连续测温的测温仪测量实验室温度或铝杯与广口保温瓶之间空气的温度，以确保漏热补偿的计算更准确，但所得结果仍然偏小，系统误差在15%以上，这表明从量热器散失到亚克力盖子的热量不可忽略. 除了明显的系统误差，理论模型与实验对象(包括装置)的对应关系不清，容易造成学生的思绪混乱，从而导致不少学生只是简单地将测量数据代入公式计算结果，该过程不利于培养学生的物理思维.

图1 实验室原有量热器实物图

2.2 真空杯做量热器

真空杯由内、外胆薄壁不锈钢筒焊接而成，内外筒之间抽真空极地大降低了传导漏热和对流漏热，内胆外壁的防辐射层降低了辐射漏热(结构见图2). 从日常经验可知，其内胆与外胆之间的漏热小，容易与式(4)的理论模型对应. 相比2.1节所述的量热器，真空杯极大地降低了实验过程中的漏热量，缺点是其内胆不像铝杯那样方便取出，无法直接测量其质量. 因此，需探索获得真空杯内胆热质量的方法.

图2 真空杯的结构图

鉴于大规模工业生产的一致性，所有同规格的真空杯内胆质量可视为相同；因此，最简单的办法是：随意挑选1个真空杯切开取出内胆，通过电子天平称量其质量，再结合实验时的盛水量即可算出内胆的热质量m1，不锈钢的比热C1可查到. 另外，采用密度小、比热小、保温效果好的发泡聚乙烯材料作为杯盖，以减少实验过程中的对流漏热，并忽略杯盖热质量对测量的影响，进一步简化物理模型.

2.3 居家测量

目前，厨房使用的电子称、温度计已很普遍，因此居家测量冰的熔化热的难点在于不能要求学生破坏真空杯，或采购与实验室完全相同的真空杯，从而无法测量实验用真空杯内胆的热质量. 居家测量冰的熔化热重点：

1)通过估算给出真空杯内胆质量的上、下限；

2)为满足式(4)所述的理论模型，操作时要求将水和冰的混合物充分摇匀，以确保内胆温度与水温一致.

基于真空杯结构(见图2)，内胆质量m1的上限不超过裸杯(不带盖子)质量mc的1/2，即m1max≈mc/2；考虑到杯盖有超过20 mm的深度，因此对于350 mL规格的真空杯，m1下限约为mc的1/3，即m1min≈mc/3.

2.4 实验仪器

原实验设备(DH4613)[6]操作复杂、采样率低，由于冰熔化过程的时间较短，不利于学生获得足够多且精度高的温度数据. 本文采用的测温仪MS6514(-200～1 372 ℃，0.1 ℃)可每秒测量并记录1个温度数据，能够解决数据量不足和精度低的问题，并能够有效降低实验仪器的成本. 另外，本文还采用了量热器[内胆为铝杯,比热为0.88 J/(g·℃)]、真空杯[内胆为304不锈钢，比热为0.46 J/(g·℃)]、电子天平(华驰,1 000 g,精度为0.1 g)等仪器设备. 在居家实验中可用厨房电子秤(分辨率为1 g)替代电子天平，温度计(分辨率为0.1 ℃)替代测温仪.

3 教学效果

3.1 3种实验方案的总体比较

在学期前4周，只有原铝杯方案；之后推出真空杯方案供学生选择，具体选情如图3所示. 2020级学生总人数为183人，其中选择方案1(铝杯量热器准连续测温，见2.1节)的学生占比约为76%，选择方案2(真空杯量热器准连续测温，见2.2节)的约占34%，选择方案3(真空杯居家实验，见2.3节)的约占20%，其中选择2种方案的约占14%，3种方案都选的学生约占7%. 3种方案的选择情况统计归纳为：测量结果的相对偏差在10%以上的占比分别为71%，27%，43%，而相对偏差在5%以内的占比分别为14%，50%，38%. 统计数据充分表明真空杯方法和居家实验的测量结果相比量热器更准确，能够引导学生选择最优实验方案. 从实验预习，实验操作、数据记录、数据分析和讨论及实验结论等方面来考察学生的学习效果，除数据分析和讨论方面学生存在个体间差异外，其他方面学生都可以达标甚至超预期完成.

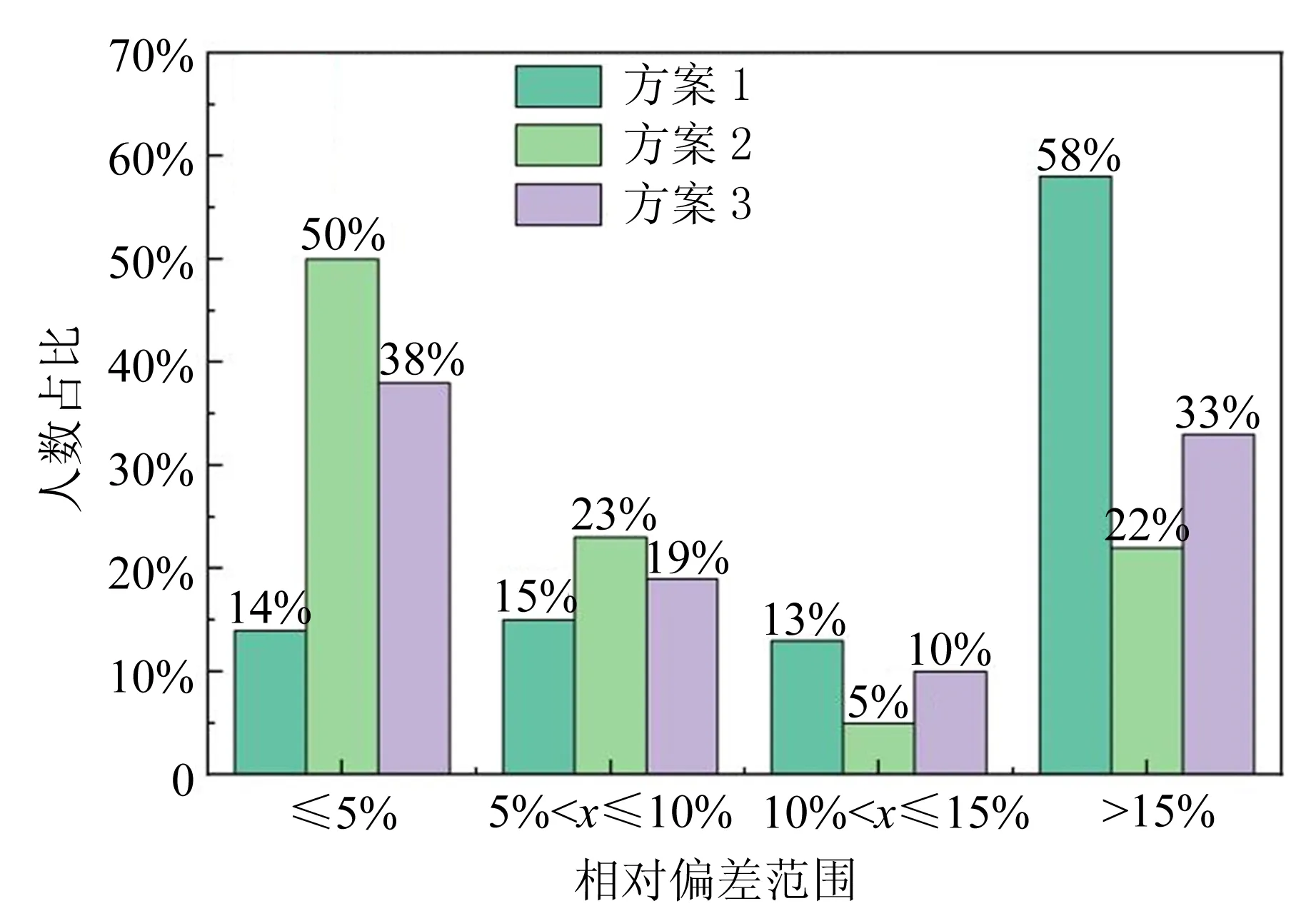
图3 学生实验数据统计情况

3.2 3种实验方案的个体比较

3种实验方案进行总体比较具有统计意义，但存在个体偏差. 7%的学生3种方案都做了，其结果可剔除个体偏差，更具可比性. 以2020级物理与天文学院黄悦铭同学的数据为例，进一步说明真空杯在该实验中的优势及其作为居家实验的可行性.

3.2.1 铝杯量热器准连续测温(方案1)

用量热器作为容器测量冰的熔化热，采用外推法和冷热补偿法处理数据(如图4所示)，得到冰的熔化热的实验值为(282±1) J/g,相对偏差为16%. 其他数据见表1.

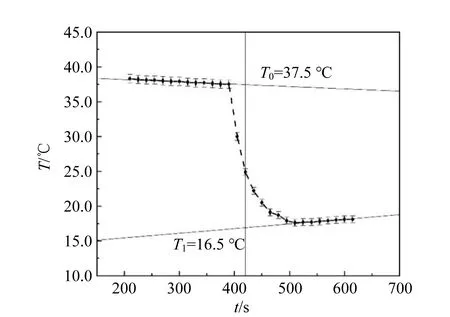
图4 采用方案1测量的温度变化数据(Te=26.7 ℃)

3.2.2 真空杯量热器准连续测温(方案2)

采用592 mL的真空杯作为容器测量冰的熔化热(如图5所示)，通过实验测量得到冰的熔化热为(331± 1) J/g,相对偏差为1%. 其他数据见表1. 实验结果表明真空杯具备较好的绝热性能，该方案为冰的熔化热的居家测量提供了依据.

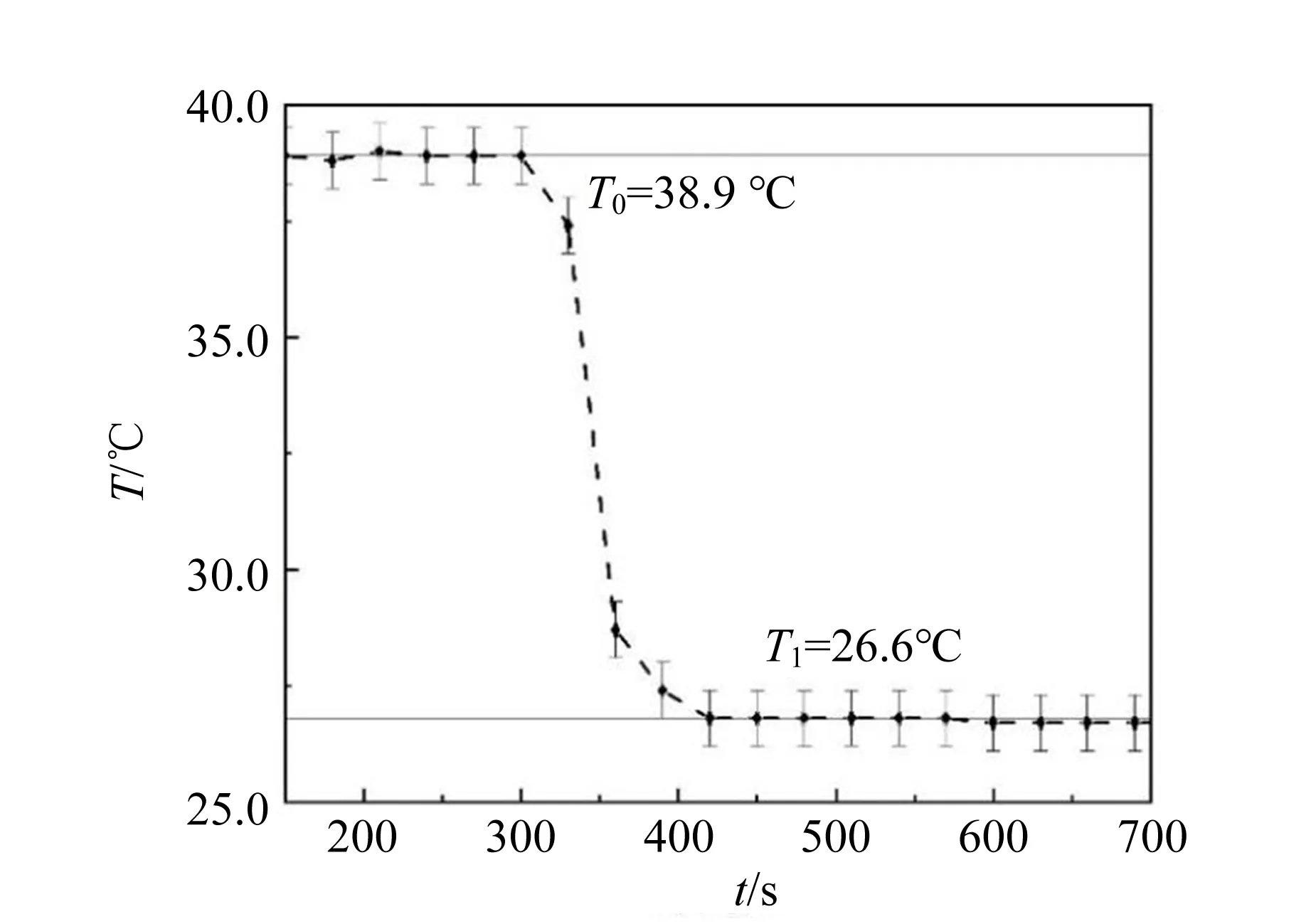
图5 采用方案2测量的温度变化数据(Te=28.2 ℃)

3.2.3 居家测量(方案3)

居家测量时可忽略实验过程的漏热量对实验结果的影响，直接测量投冰之前和冰熔化后的水温作为初温T0和末温T1. 真空杯内胆的热质量参考2.3节的估算方案. 通过实验得到冰的熔化热测量结果为(349±1) J/g，相对偏差为5%，实验数据如表1所示.

表1 3种实验方案测量冰的熔化热的实验数据

3.3 教学效果

量热器作为最初的实验设计，优势在于内胆可直接取出进行热质量的测量. 其缺点是需要学习漏热补偿方法，且理论模型与实验对象的对应有缺漏，从而影响学生物理建模能力和物理思维的培养.

增加真空杯测量冰的熔化热的实验内容后，有效地减小了实验过程中的漏热，并使冰的熔化热测量的理论模型与实验对象更贴合. 对比方案1，学生更容易理解实验过程中的漏热对冰的熔化热测量结果的影响. 为让学生更清楚地了解真空杯的内部结构，可切开真空杯供学生观察. 由于真空杯的绝热效果好，投冰前5 min和冰熔化后5 min的水温几乎恒定(如图5所示)，因此无需做漏热补偿处理，处理数据时直接将初温和末温代入式(4)，即可计算出冰的熔化热. 这也成为了该实验可作为居家实验的依据.

居家测量方案中，操作成为影响实验误差的主要因素. 比如如何判断温度是否达到均匀，或多久才能使内胆温度等于水温，并且每个学生对充分摇匀的理解也不一样，有的轻摇，有的猛摇；另外，内胆质量所需要的估算分析也是一年级学生所不擅长的. 这都是造成居家测量误差在统计上比方案2的测量误差大的原因(2.2节所述). 在对实验方案有充分理解和操作经验的情况下，使用如图3所示的厨房设施(精度比实验室设备低1个数量级)，在内胆质量估算占真空杯祼质量的1/3～1/2时，测得冰的熔化热在339～346 J/g之间，相对偏差在1.5%～3.7%之间. 从存在操作不熟练、量热器质量不确定(需要估算)等问题的学生测量结果来看，方案2和方案3的统计结果仍优于方案1，充分显示了真空杯作为量热器的优势. 最后，正确引导学生操作及思考其与理论模型间的关系，是居家实验的重要环节. 根据真空杯的具体结构参量，参考式(4)中的热质量M，即可进一步精细化测量结果.

在改进实验方案后，学生从物理模型的建立、数据测量、实验操作以及误差分析等实验的整个过程都有了更加深入的理解. 据调查问卷显示，84.5%的学生表示掌握了实验操作和热学测量的方法，学会了冰的熔化热测量的物理原理；4%的学生表示对实验得心应手. 但仍有部分学生对该实验存在疑惑，因此下一步仍须努力让更多的学生真正参与到实验的学习中并有所收获.

4 结束语

为提高冰的熔化热测量实验的精度，加强物理建模能力的培养，提高学生实验学习的获得感，增强学生对热学实验的兴趣，本文采用真空杯作为量热器测量冰的熔化热，一方面降低了实验过程中的漏热量，减小了实验误差；另一方面，采用简单的结构简化了实验系统，并与理论模型有了更清晰地对应，从而有利于培养学生理论联系实际的能力. MS6514测温仪与真空杯的组合不仅提高了数据量和测量的精度，还降低了实验成本. 另外，真空杯的实验方案可进一步拓展到居家实验中，为大学物理实验或疫情防控常态化的实验教学提供可行性方案.