乌东德水电站明满流尾水洞瞬态水力特性研究
2021-11-29何相慧杨桀彬杨建东
何相慧,杨桀彬,杨建东,李 玲
(1.武汉大学水资源与水电工程科学国家重点实验室,武汉430072;2.长江勘探规划设计研究有限责任公司,武汉430072)
0 引 言
导流洞作为尾水洞不仅可以优化地下输水系统的布置,增加围岩稳定性,也可以节省施工成本和周期。但是尾导结合的水电站在下游水位较低的甩负荷工况下,容易出现明满流交替的现象[1,2],尾导结合段水深较浅会导致出现水流中断现象[3],水位上升下降的过程中,还可能会残留大量气体在洞顶形成气泡[4]。另外,有压流工况下,斜坡段末端产生负压,较大的负压会产生水柱分离,对水工结构产生严重影响。
目前,对于水电站过渡过程计算主要有一维数值计算、三维数值计算和模型实验3种方法。明满流一维数值计算方法有窄缝法[5,6]、激波拟合法[7]、刚性水击法[8]等,其中,虚拟狭缝法被广泛应用于工程实践中。采用基于VOF 模型的三维计算方法研究明满流过渡过程中的水流状态,已被证明与实验和一维计算有较好的吻合性[9-11],为研究明满流状态下的流场状态提供了参考。由于实验条件的限制,大部分的模型实验只进行稳态工况的实验,采用一维和三维进行数值模拟就显得更加重要。
本文对乌东德水电站右岸某水力单元进行了一维和三维数值模拟,研究其在有压流和明满流过渡过程中的水力现象,重点关注有压流工况下的洞顶负压、明满流工况下的明满流波动范围、是否产生水流中断、洞顶气囊的演变规律等,以期为相应的工程实践提供参考。
1 计算方法
1.1 一维明满流虚拟狭缝法
明满流尾水系统非恒定流计算中,需同时考虑有压流的非恒定水击方程和明渠非恒定流的数学方程,并正确处理明满流分界面的运动。
有压非恒定流的基本方程为:
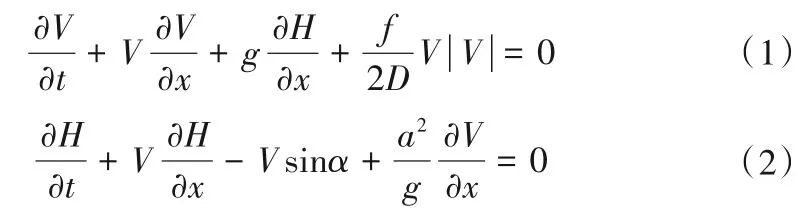
明渠非恒定流的基本方程为:
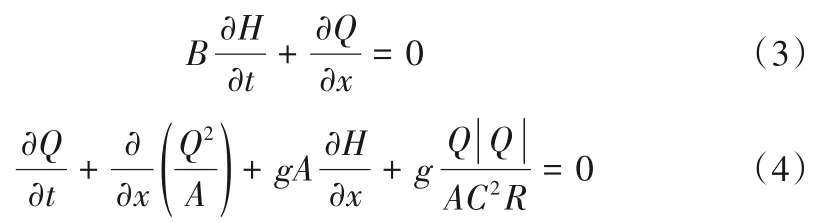
式中:H为水头,m;Q为流量;A为过水断面面积,m2;B为水面宽度,m;R为水力半径,m;C为谢才系数,m0.5/s;x为沿渠长的水平距离,m;t为时间,s;g为重力加速度,m/s2;V为管道中的流速,m/s,由上游流向下游为正;f为沿程损失系数;D为管道直径,m;a为水锤波波速,m/s。
采用虚拟狭缝法计算明满流交替分界面的运动,则有压非恒定流可以采用明渠非恒定的方程进行计算,缝隙宽度B 满足以下方程

1.2 基于VOF模型的三维CFD计算方法
VOF 模型适用于求解两种互不掺混的流体,通过求解单独的动量方程和处理穿过区域的每一流体水位容积比来模拟。VOF 方法最早为20 世纪80年代,由Hirt 与Nichols 提出[12]。它的基本原理是利用被研究流体的体积与网格单元的体积比函数F,以确定自由液面的网格。对于气-液两相流而言,设A 相为气体,B相为液体,当FA= 0时,说明没有气体,即全部被液体充满;当FA= 1 时,说明该网格内全部是气体。当0 <FA<1时,说明该网格单元含有气-液交界面,也就是自由液面。当然,在每个网格单元中,FA+FB= 1,即气-液两相体积分数和为1。

图1 虚拟狭缝法示意图
在VOF 模型中,对相与相之间的交界面进行追踪是通过求解某一相或多相之间的连续性方程实现,对于水和空气作为两相的流动,连续性方程为:
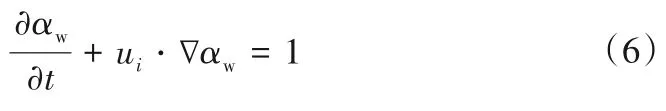
2 计算模型与边界条件
2.1 计算模型
计算区域从机组尾水管出口到下游部分水库,岔管底板高程776 m,调压室底板高程802 m,尾水洞出口底板高程800 m,导流洞底板高程为800 m,整体管道长760.85 m,一维和三维模型图如图2 和图3 所示,为了监测过渡过程中洞顶压力随时间的变化,设置22个监测点,位置如图4所示。

图3 三维计算模型
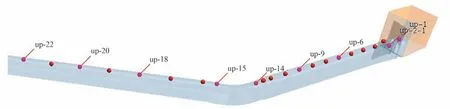
图4 洞顶监测点设置
2.2 边界条件
本文的计算工况选取下游高水位和低水位的甩负荷工况,三维计算采用Creo2.0 进行建模,采用Star-CCM+进行网格划分和数值计算,网格基本尺寸为0.8 m,连接管及大井敞开段进行网格加密,总网格数70.81 万。入口设置为质量流量入口,出口设置为压力出口(图3),质量流量曲线由Topsys 导出的体积流量(图5)转换而来。调压室顶部设置为压力出口,相对压力为0 atm。湍流模型采用Realizablek-ε[13],固壁边界设置为无滑移壁面,近壁区采用标准壁面函数法处理。根据下游水位设定调压室初始水位,进行恒定流计算使水位稳定,再以此为初始条件进行甩负荷计算。
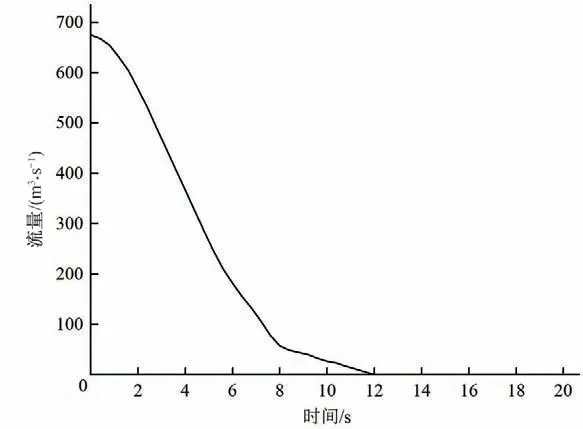
图5 进口边界条件
3 计算结果与分析
3.1 一维与三维计算结果对比分析
表1 为两个工况下调压室涌浪和底板压差的对比,从表1中可以看出,有压流工况与明满流工况下一维与三维的初始水位差值分别为1.26 m和1.38 m,三维计算的沿程损失小于一维,这与管道阻抗系数等的选取有关。由图6 和图8 可以看出,一维和三维计算结果的涌浪波动变化趋势相同,涌浪水位均随时间周期性衰减。有压流工况的涌浪周期分别为107.5 s(三维)和107.36 s(一维),两者差值为0.14 s;明满流工况的涌浪周期分别为178.6 s(三维)和170.2 s(一维),两者差值为7.4 s,明满流工况下的顶部气囊,局部流动旋涡,吸气旋涡等对波的传播均有影响,一维计算时无法将这些因素考虑在内,因此其周期有一定的差值。由图7 和图9 可以看出,一维计算和三位计算的底板压差随时间的变化规律相同。由以上分析可得,一维计算和三维计算具有较好的契合度,相互印证了计算的准确性。
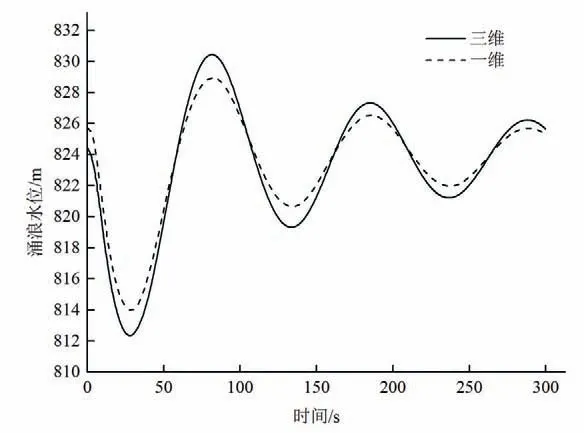
图6 有压流工况涌浪水位对比
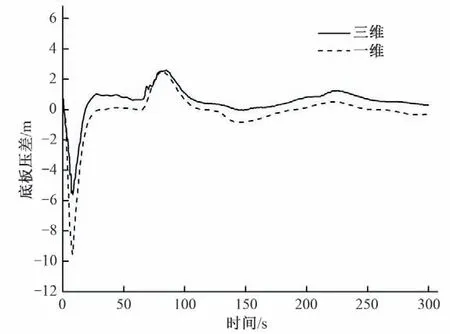
图7 有压流工况底板压差对比
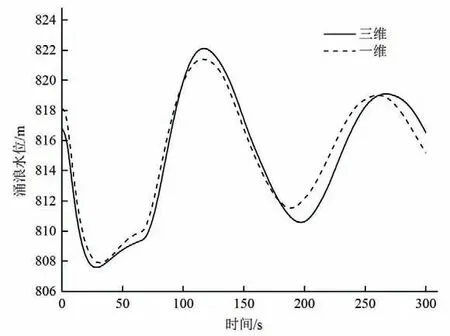
图8 明满流工况涌浪水位对比
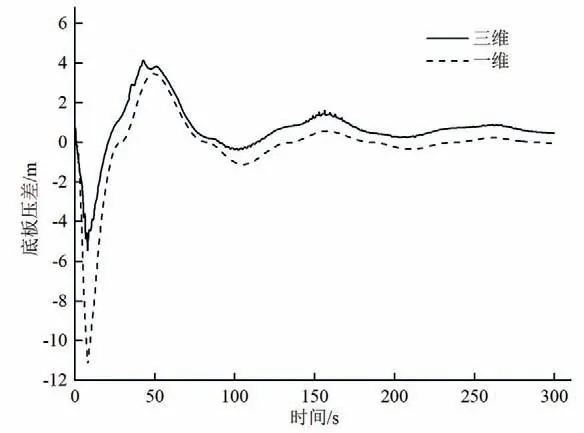
图9 明满流工况底板压差对比
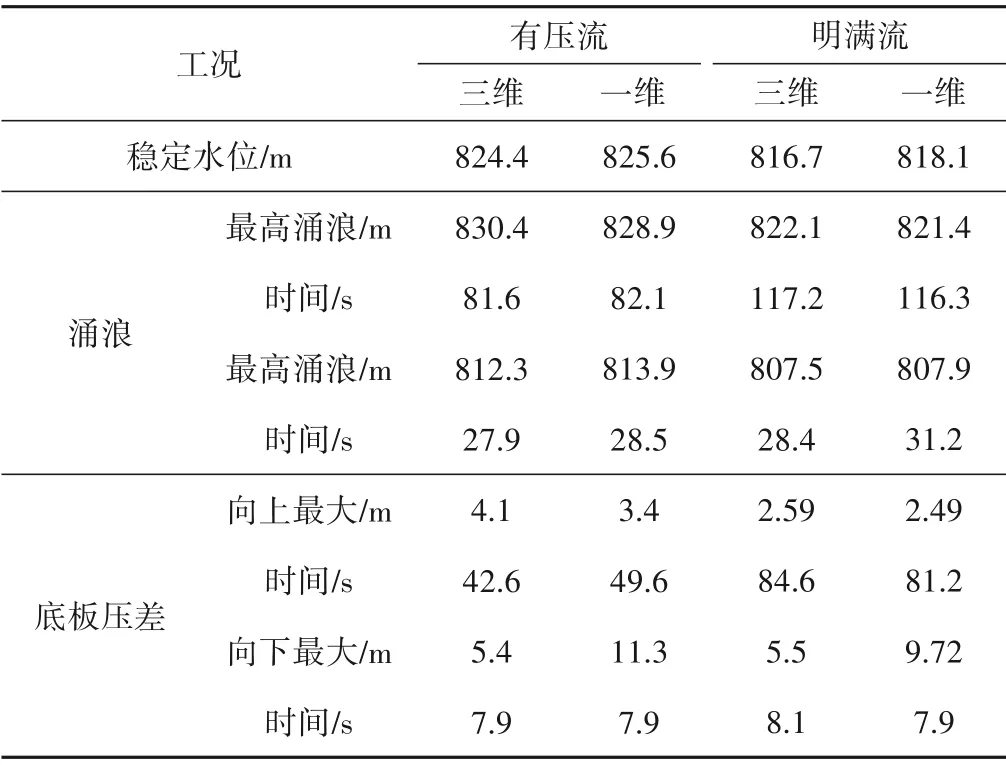
表1 调压室涌浪水位对比
由一维topsys计算得到的最高压力包络线和最低压力包络线和由三维洞顶监测点压力监测数据得到的洞顶压力包络线如图10 所示。最大压力包络线和最小压力包络线与洞顶高程线的交点所形成的区域为明满流范围。由该图可知,一维和三维明满流波动范围基本重合,三维计算的明满流范围偏向下游。
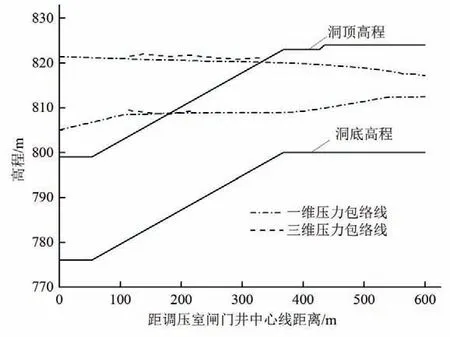
图10 明满流范围
选取尾导结合点的洞顶压力进行对比,尾水洞顶的压力变化随着尾水洞内水流的周期往返运动呈现周期性衰减过程(图11)。在甩负荷开始,尾水洞内流量减小,洞顶出现负压,在流量减小最快时刻(与流出调压室流量最大时刻同步),负压达到极值。之后由于调压室补水流量较大,流出尾水洞流量减小,尾水洞顶负压减小。由图11的结果对比可以看出,一维和三维计算结果的波动规律一致,都随时间变化做周期性衰减波动。
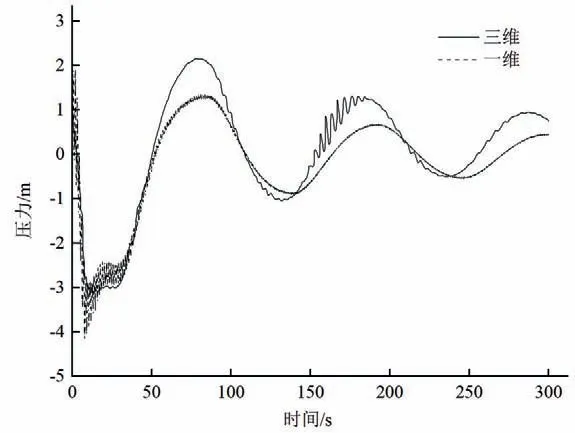
图11 尾导结合点洞顶压力对比
3.2 明满流分界面
图12为尾导结合处甩负荷工况下的水位波动变化图,由图12可以看出,甩负荷初始状态,导叶逐渐关闭,尾水洞内引用流量减小,调压室水位下降,明满流界面向上游移动。随着流出调压室流量增加,明满流界面向上游推进的速度减缓。由表1和图8 可知,甩负荷28.4 s 调压室达到最低涌浪位置,明满流波动由于水流惯性继续向上游移动,速度减缓为零后做反向运动。甩负荷85 s 后,流入调压室流量加大,明满流界面向下游移动速度加快。明满流界面和调压室水位不断做周期性往返运动。由图12可以看出,在明满流界面向下游快速移动的过程中,会产生一系列的残留气囊,这些气囊随明满流界面向下游移动、融合、减小、消失。
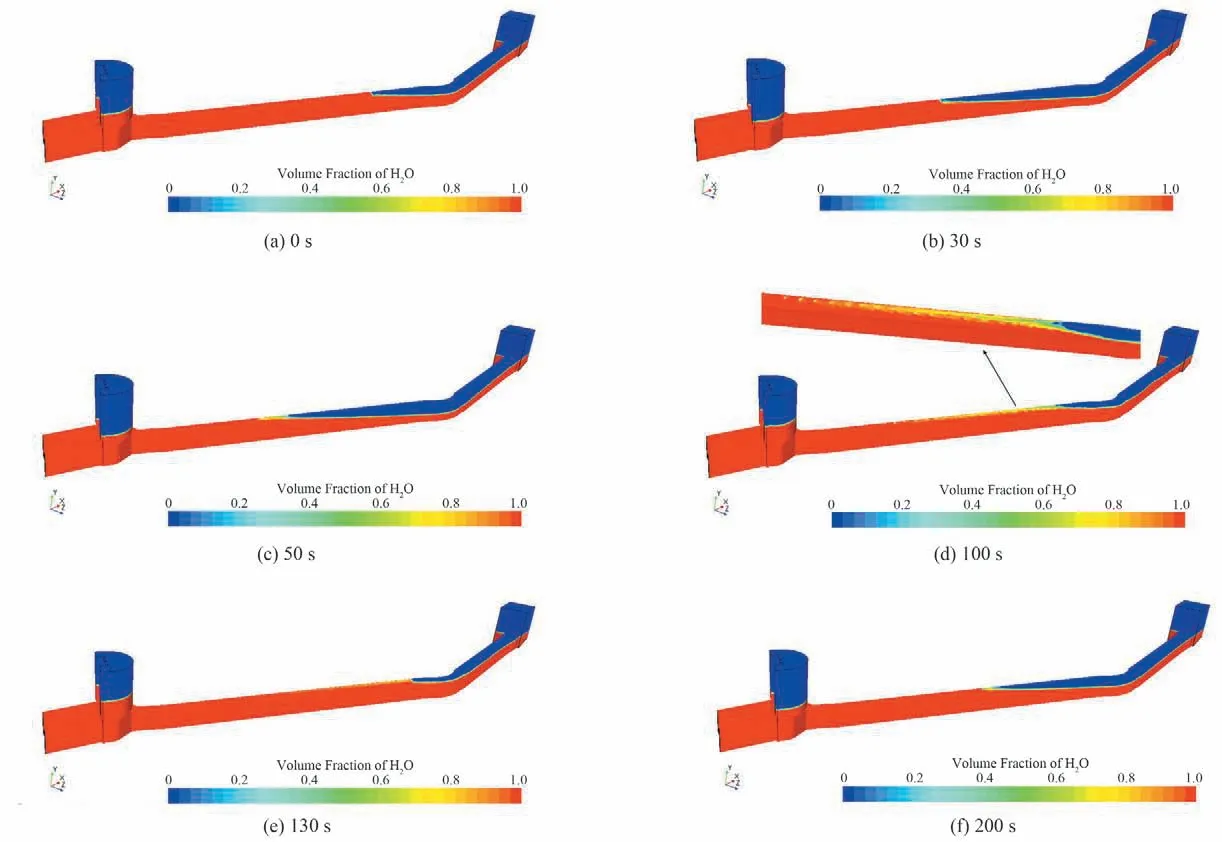
图12 转弯处明满流波动
明满流界面在up-17~up-22 之间移动,图13 为斜坡段监测点的洞顶压力随时间的变化图。图中可以看出,尾水洞顶压力随时间做周期性衰减运动,明流区洞顶压力为零,满流区洞顶压力与明流段水深正相关。在甩负荷后75 s 时由于明满流界面向下游移动速度较快,产生了一连串的大气泡,up-18~up-22均受到影响产生较大的阶跃值,靠近下游的监测点up-19 的阶跃跳动最大。
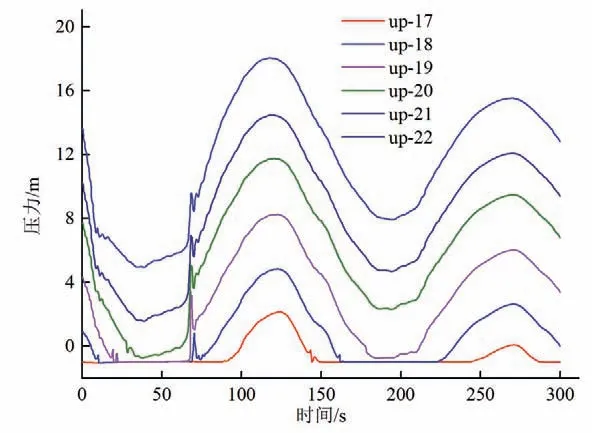
图13 斜坡段洞顶压力变化图
尾水洞导尾结合段底板高程为800 m,下游尾水位815.83 m的大波动过渡过程中,可能发生尾水洞内某处水深过低,该处弗劳德数Fr 接近1 甚至大于1,而发生水流中断的现象。从计算结果看,导尾结合点的水深最小为10.19 m,导尾结合点所在断面在大波动过渡过程中弗劳德数Fr 变化范围均在0 到0.2 之间,未达到接近1而导致断流的条件。
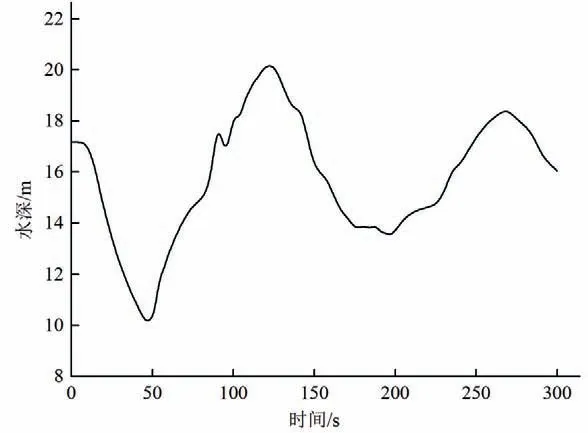
图14 导尾结合点水深变化过程
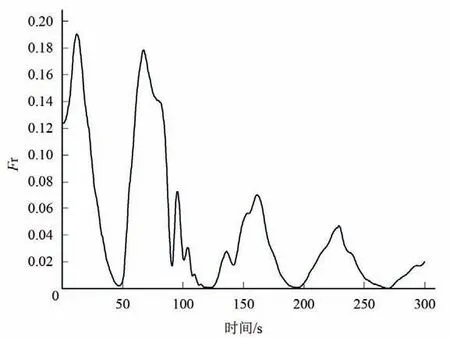
图15 导尾结合断面弗劳德数变化过程
4 结 论
本文对一台尾导结合的水电站进行了高水位和低水位甩负荷的过渡过程计算,通过以上分析可知:
(1)有压流工况和明满流工况下,一维和三维计算基本吻合,调压室涌浪周期差值均在8 s以内。
(2)明满流工况下,尾水洞顶压力随时间做周期性衰减运动,明流区洞顶压力为0,满流区洞顶压力与明流段水深正相关,洞顶残留气囊的破裂会产生压力的阶跃值。
(3)明满流界面向下游移动时,会产生一系列的洞顶残留气囊,这些气囊会逐渐发展、融合和溃灭,在溃灭时会对洞顶产生一定的冲击压力。
(4)尾导结合处水深弗劳德数可作为判断该处是否产生断流的参数,该水电站过渡过程中,尾导结合处水深始终为正值,弗劳德数变化范围均在0到0.2之间,未产生断流。 □
