高填方黄土明洞顶EPS板和土工格栅共同减载计算及土拱效应分析

李　盛,卓　彬，王起才,马　莉,宁贵霞,贾　涛

(1.兰州交通大学 道桥工程灾害防治技术国家地方联合工程实验室，甘肃 兰州　730070；2.兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州　730070；3.兰州工业学院 土木工程学院，甘肃 兰州　730050；4.成昆铁路有限责任公司 工程技术部，四川 成都　610081)

随着西部高速铁路的建设，由于西部黄土高原地区特殊的地理环境，将不可避免地修建高填方明洞。因高填方明洞顶上覆土荷载往往较大，造成结构受力复杂，为减小高填方明洞顶实际土压力，保证明洞结构安全，应对高填方黄土明洞顶土压力的减载措施进行研究。

国内外学者在土压力减载方面已有诸多研究，并取得了相应的成果。对于涵洞(管)土压力减载方面的研究，顾安全[1-3]对涵顶铺设柔性材料EPS板进行了多项室内试验，假设涵洞两侧填土为半无限均质线性变形体，并考虑涵洞外形影响，得出了采用该减载措施的涵洞垂直土压力计算公式；王晓谋[4]以相似理论为基础，将柔性材料铺设在涵洞顶进行模型试验，推导了涵洞顶铺设柔性材料的垂直土压力计算公式；杨锡武[5]通过室内及现场试验，对加筋减载孔的尺寸、加筋层数以及锚固区的宽度给出了理论计算方法；郑俊杰[6]通过理论研究建立了加筋减载涵洞受力计算模型，并对涵洞顶柔性填料进行受力分析，推导了适用于加筋桥减载结构涵洞顶土压力的计算公式；Okabayashi[7]对埋设于干砂中的箱涵进行了柔性材料减载的离心模型试验，研究了填有柔性材料的高填方涵洞的减载效果；Sun[8]运用有限元程序FLAC4.0研究了深埋涵洞顶铺设轻质泡沫材料后涵洞顶土压力的变化规律。这些研究成果已经在实际工程中取得广泛应用，但鉴于明洞与涵洞结构高度和跨度的差别，这些研究成果不能直接应用于明洞中。对于明洞顶土压力减载方面的研究，文献[9—11]通过室内试验分析了明洞上方分别铺设EPS板、土工格栅、EPS板和土工格栅进行减载的洞顶土压力变化规律，提出了仅铺设土工格栅减载的明洞顶土压力计算公式，并通过现场试验证明了所推计算公式的正确性。但对EPS板和土工格栅共同减载的明洞顶土压力理论计算方法研究不足。因此，本文以兰渝铁路某明洞为例[17]，推导高填方黄土明洞顶铺设EPS板和土工格栅共同减载的明洞顶土压力计算公式，并通过数值模拟证明该减载方法的良好效果及计算方法的正确性。最后，从明洞上方土体应力和位移的云图揭示EPS板和土工格栅共同作用的减载机理，即分析其土拱效应。

1　明洞顶减载后的土压力计算公式推导

在明洞顶同时铺设EPS(Expanded Polystyrene)板和土工格栅，EPS板促使填土过程中产生土拱效应，土工格栅变形产生向上的“提兜”力，二者共同作用使明洞顶的土压力传递到外土柱上[8]，从而实现明洞顶土压力的减载。

首先做以下基本假设：①高填方明洞顶与两侧填土之间的作用面相互垂直；②计算模型为平面应变问题[6,12-13]；③EPS板和土工格栅的重量均忽略不计。

基于以上假设，根据土压力减载机理，建立高填方黄土明洞顶铺设EPS板和土工格栅共同减载的计算模型，如图1所示，推导该减载措施下的明洞顶土压力计算公式。图1中：h为明洞高度，m；Hs为明洞顶至等沉面距离，m；H为地基顶至等沉面距离，m；D为明洞宽度，m；θ为土工格栅变形后在内外土柱交界处的水平倾角，rad；δ8为格栅中心竖向最大位移，m；T为单位宽度土工格栅受到的拉力，kN·m-1；q1为土工格栅下表面土体作用力，kPa；q为土工格栅上表面荷载，kPa；δ1，δ3，δ4，δ6分别为明洞顶Hs土层的压缩变形量、EPS板的变形量、明洞结构的变形量及明洞地基的变形量；δ2，δ5，δ7分别为明洞高度范围内两侧外土柱的压缩变形量、明洞顶两侧填土的压缩变形量和明洞两侧地基的变形量。

图1　明洞顶EPS板和土工格栅共同减载的计算模型

1.1　EPS板和土工格栅变形的相互关系

在填土压力作用下,等沉面以下土体将产生压缩变形。假设减载作用是由内外土柱间土体相对变形产生的摩擦所致，则由等沉面以下土体压缩变形的相互关系可得

δ1+δ3+δ4+δ6=δ2+δ5+δ7

(1)

当明洞及地基本身均为刚性时，δ4，δ6，δ7均为0，则式(1)变为

δ1+δ3=δ2+δ5

(2)

减载后明洞顶平面内土柱的沉降大于外土柱的沉降，设其沉降差为-δ，则有

δ1-δ2=-δ

(3)

将式(3)代入式(2)得

δ5-δ3=δ1-δ2=-δ

(4)

由于格栅的变形是由内外土柱产生的相对变形引起的，因此，格栅中心竖向最大位移δ8即为内外土柱沉降差δ。

1.2　EPS板和土体相对变形引起土压力的变化

根据顾安全公式[2]，假设明洞两侧填土为半无限均质线性变形体，通过作用在明洞顶均布附加土压力p1，并考虑线性变形体具有一定的侧膨胀，推算出明洞顶平面内外土柱的相对沉降差δ为

(5)

式中：wc为与刚性构筑物长宽比及基底形状有关的系数；ν为明洞顶以上填土泊松比；E为明洞顶以上填土变形模量，kPa。

因此，通过沉降差δ的弹性理论解，根据式(1)可反算明洞顶减载的土压力p1。

根据EPS板的应力—应变曲线[3]，应变在60%以后对应的阶段为硬化阶段，考虑保证EPS板留有一定的安全储备，因此，取EPS板厚度h1的60%作为压缩变形量，即δ3=0.6h1，将其代入(4)式可得

δ=0.6h1-δ5

(6)

再将式(6)代入式(5)并整理可得明洞上方铺设EPS板可减载的土压力p1为

(7)

1.3　土工格栅变形引起土压力的变化

明洞顶的EPS板被压缩，格栅发生向下挠曲，格栅底部土体对其有一定的向上支撑作用。文献[14]指出，当不考虑松散填料的支撑作用时格栅的挠曲变形为悬链线，反之，格栅变形较小，格栅的挠曲变形曲线可近似为圆曲线。因此，明洞顶土工格栅的变形曲线近似采用圆曲线。

取变形后格栅的中心点为坐标原点、水平方向为x轴、竖向为y轴，建立直角坐标系，如图2所示。土工格栅变形后在内外土柱交界处的水平倾角θ等于圆曲线在该处的切线与水平线的夹角。基于土工格栅弹性变形，得到其单位宽度竖向受力平衡方程为

q1D=qD-2Tsinθ

(8)

其中，

T=εE1A

(9)

式中：E1为土工格栅弹性模量，kN·m-3；A为单位宽度土工格栅面积，m2；ε为土工格栅应变。

图2　土工格栅计算模型

则明洞上方铺设土工格栅可减载的土压力p2为

p2=qD-q1D

(10)

土工格栅变形后在内外土柱交界处的水平倾角θ等于圆曲线在该处的切线与水平线的夹角。根据格栅受力变形的几何关系可得

(11)

由J.P.Giroud推得土工格栅在受力作用下产生的应变方程[15-16]为

(12)

将式(9)，式(11)和式(12)代入式(10)并整理可得

(13)

1.4　明洞顶减载后的土压力

当明洞顶同时铺设EPS板和土工格栅时，则作用在明洞顶的土压力p为

p=γ(H-h)-p1-p2

(14)

式中：γ为填土重度，kN·m-3。

假设明洞顶内土柱土压力的减小值由两侧外土柱平均承担，故作用在明洞两侧的填土压力为

(15)

取明洞两侧填土的压缩模量为E2，则可根据式(15)求得明洞两侧填土的压缩变形δ5，即

(16)

采用Matlab对式(6)、式(7)、式(13)—式(16)进行迭代计算，得到明洞顶铺设EPS板和土工格栅共同减载后的明洞顶土压力p。

2　有限元模拟

以兰渝铁路某明洞为例[17]，采用有限元软件ANSYS模拟EPS板和土工格栅共同减载后的明洞顶土压力，并将模拟结果与上述计算结果进行对比分析，以验证其合理性。

有限元模型中：明洞、EPS板、土工格栅均采用弹性材料模拟，黄土、地基采用摩尔—库伦弹塑性材料模拟；土工格栅与土体之间的相对位移和变形采用库伦滑动模型模拟。网格划分以四边形为主，三角形为辅，分别限制模型底部水平和竖向位移、两侧水平位移，如图3所示。填土高度为30 m，EPS板和土工格栅分别铺设在距明洞顶0和7.5 m处。土工格栅横截面面积A=0.005 m2，其余各材料参数见表1。为得到内外土柱不同沉降差δ与明洞顶减载后的土压力相互关系，EPS板的弹性模量分别取1.0，0.9，0.8，0.7，0.6，0.5 MPa。通过定义时间步的方法模拟分层填筑过程，数值模拟每个时间步的应力场和位移场。

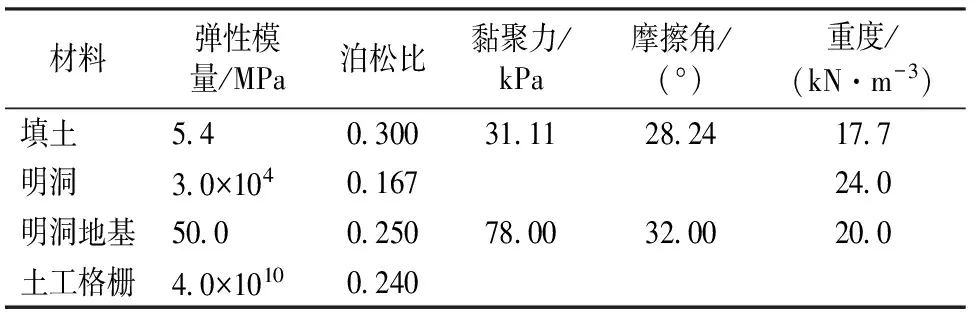
表1　计算参数

图3　计算模型网格划分

为了说明土工格栅中心竖向最大位移δ8等于内外土柱沉降差δ，提取明洞顶铺设不同弹性模量EPS板引起两者之间的变化关系曲线，如图4所示，由图4可知，2条曲线几乎完全吻合，证明两者相等。这也与式(4)的计算结果(假设明洞及其地基为刚性时，δ5-δ3=δ1-δ2=-δ)吻合。

图4　δ与δ8随EPS板弹性模量变化关系

图5(a)为不同弹性模量EPS板减载的明洞顶宽度范围内数值模拟的土压力分布曲线。由图5可知，明洞顶宽度范围内土压力大致呈“波浪形”分布，且土压力随EPS板弹性模量的减小而减小。为了与计算结果进行对比，采用荷载等效方法，将图5(a)所示的明洞顶土压力分布曲线等效为均布荷载，等效计算图如图5(b)所示。

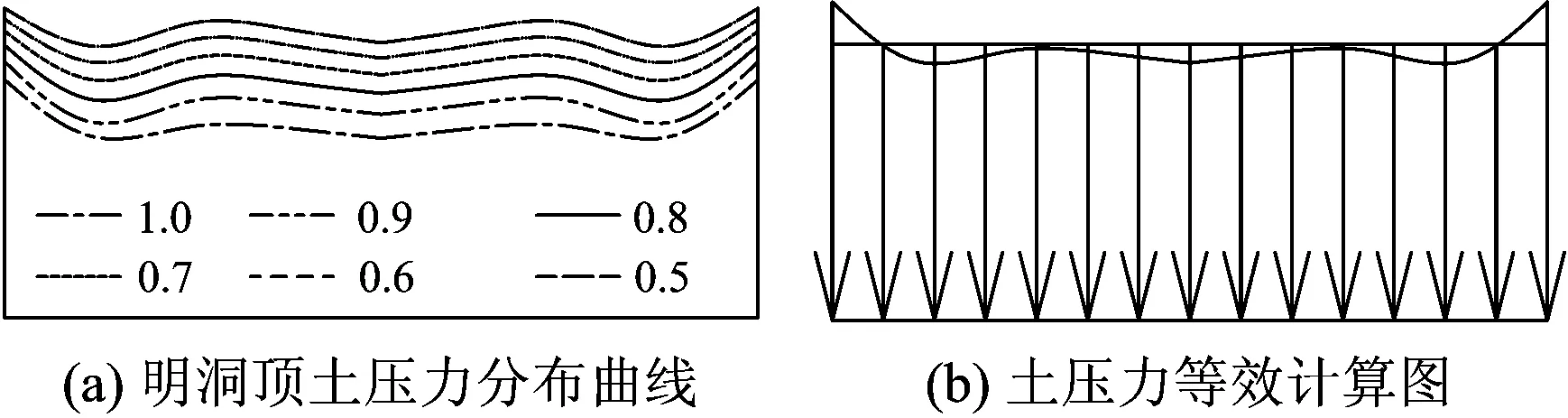
图5　明洞顶土压力有限元计算结果(单位：MPa)

图6为明洞减载后土压力的计算结果与数值模拟结果随沉降差δ的变化规律。由图6可知：公式计算结果与数值模拟结果的数值基本相同、变化规律相似，即明洞顶土压力均随内外土柱沉降差的增大而减小；当内外土柱沉降差δ=18 cm时，公式计算与数值模拟结果几乎相等；当沉降差δ<18 cm时，公式计算与数值模拟结果最大相对误差为-3.39%；当沉降差δ>18 cm时，公式计算结果与有限元计算的结果最大相对误差为3.59%。从而验证了计算公式的合理性。

图6　明洞顶土压力随内外土柱沉降差的变化规律

3　土拱效应

通过上述数值模拟明洞顶的土压力和竖向位移，揭示了在明洞顶同时铺设EPS板和土工格栅时其共同作用的减载机理，即明洞顶产生了土拱效应，减弱了明洞顶土压力的增长速度。

取EPS板的弹性模量为0.5 MPa，采用建立的有限元模型模拟明洞顶土体的竖向位移、最小主应力和竖向应力，结果分别如图7—图9所示。

由图7可知：明洞上方土体的竖向位移较大，内外土柱产生了不均匀沉降，沉降差为22 cm；这是由于明洞顶EPS板压缩变形引起内外土柱沉降差。由图8可知：明洞顶最小主应力方向发生旋转,指向外土柱，最小主应力方向连线大致呈拱形，出现了明显的“应力拱”，且明洞顶最小主应力分布密度明显小于明洞两侧，说明明洞顶荷载可通过“应力拱”传递到明洞两侧。由图9可知：明洞顶土体竖向应力明显小于两侧土体竖向应力，洞顶为300 kPa，而明洞两侧竖向应力较大，为600 kPa；这是由于“应力拱”的存在将明洞顶荷载通过土拱转移至明洞两侧，使得明洞顶竖向应力相对较小。

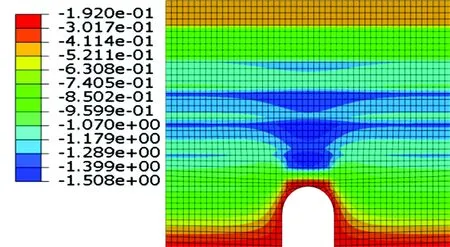
图7　竖向位移云图(单位：cm)

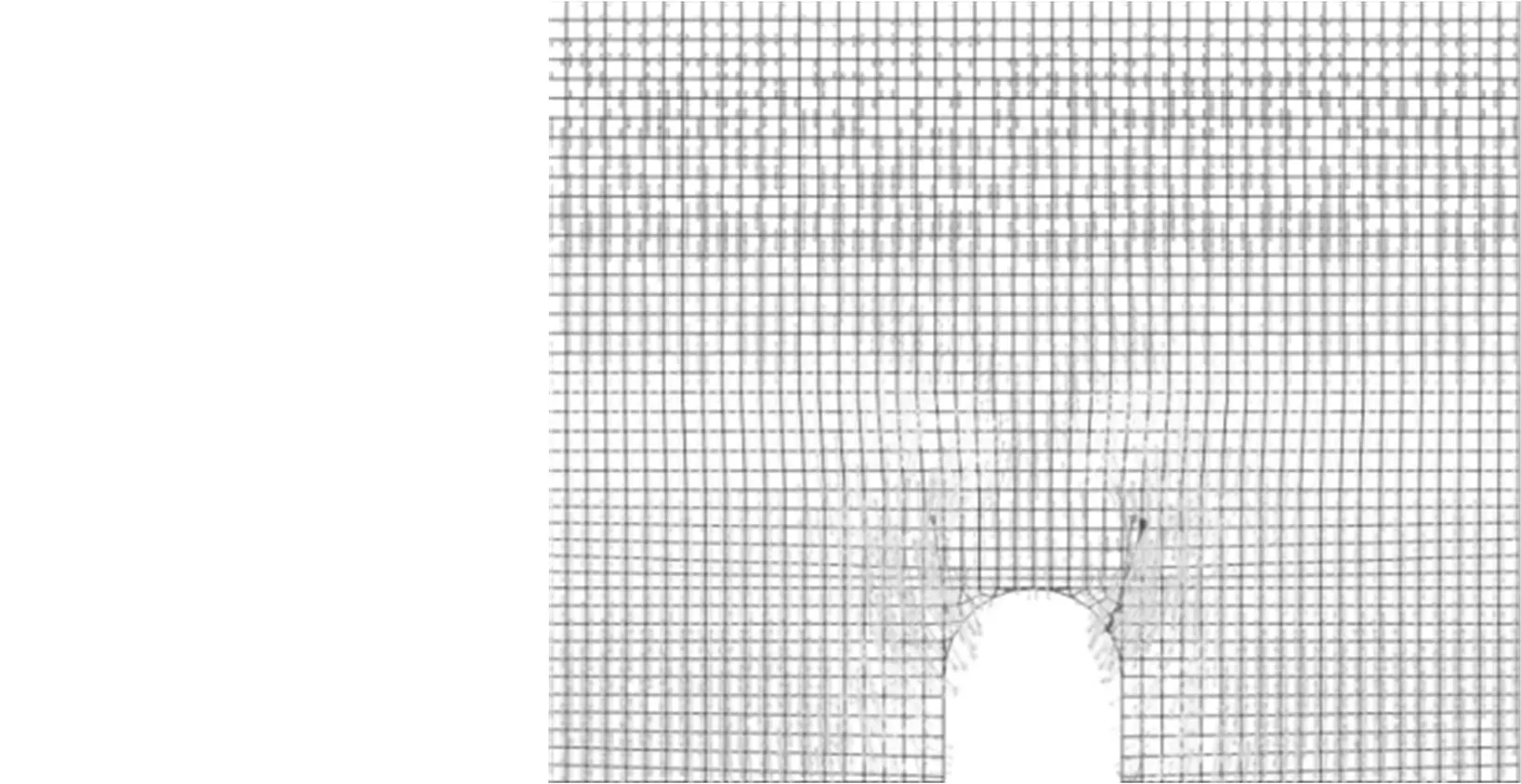
图8　最小主应力矢量图

图9　竖向应力云图(单位：kPa)

图10为洞顶不同高度处横向土压力的变化曲线。由图10可知：随着与明洞顶间距离的增大，EPS板顶横向土压力先增大后减小，大致呈“拱形”分布；在距明洞顶7.5 m(0.83倍洞高)，即铺设土工格栅位置处，横向土压力达到最大值，出现了明显的“应力拱”，“应力拱”处横向应力最大，“应力拱”下部竖向、横向土压力均减小，说明荷载通过土拱传递到明洞两侧土体中。

图10　明洞顶不同高度处横向土压力的变化曲线

4　结　论

(1)针对明洞顶同时铺设EPS板和土工格栅减载措施，推导了减载后的明洞顶土压力计算公式。在不同沉降差下，公式计算结果与有限元模拟结果均表明，明洞顶土压力均随内外土柱沉降差的增大而减小，且公式计算结果与有限元模拟结果最大相对误差为3.59%，验证了减载后的明洞顶土压力计算公式的正确性，可为高填明洞减载设计提供参考。

(2)对减载措施下明洞顶土体的竖向应力、最小主应力和竖向位移的数值模拟结果分析可知：内外土体沉降差的存在导致明洞顶最小主应力发生偏转，引起明洞顶竖向应力减小，两侧竖向应力增大，产生土拱效应；在0.83倍洞高处，横向土压力分布达到最大值，出现“应力拱”；且沉降差越大，“应力拱”横向土压力越大，明洞顶处垂直土压力减小越显著。

[1]顾安全，郭婷婷，王兴平. 高填土涵洞(管)采用 EPS 板减荷的试验研究[J]. 岩土工程学报，2005，27(5)：500-504.

(GU Anquan，GUO Tingting，WANG Xingping.Experimental Study on Reducing-Load Measurement Using EPS of Culvert under High-Stacked Soil[J].Chinese Journal of Geotechnical Engineering，2005，27(5)：500-504. in Chinese)

[2]顾安全.上埋式管道及洞室垂直土压力的研究[J]. 岩土工程学报，1981，3(1)：3-15.

(GU Anquan. Investigation of the Vertical Earth Pressure on Projecting Conduit and Underground Chamber under a High Embankment [J].Chinese Journal of Geotechnical Engineering，1981，3(1)：3-15. in Chinese)

[3]顾安全，吕镇锋，姜峰林，等.高填土盖板涵EPS板减荷试验及设计方法[J]. 岩土工程学报，2009，31(10)：1481-1486.

(GU Anquan，LÜ Zhenfeng，JIANG Fenglin，et al.Load Reduction Tests and Design Methods for Culverts with High Fill Soil Using EPS Slabs[J].Chinese Journal of Geotechnical Engineering，2009，31(10)： 1481-1486. in Chinese)

[4]王晓谋，顾安全.上埋式管道垂直土压力的减荷措施[J]. 岩土工程学报，1990，12(3)：83-89.

(WANG Xiaomou，GU Anquan.Research on Methods of Vertical Earth Pressure Reduction on Top-Buried Pipes[J].Chinese Journal of Geotechnical Engineering，1990，12(3)：83-89. in Chinese)

[5]杨锡武.山区公路高填方涵洞土压力理论及加筋减载研究[D]. 重庆：重庆大学，2005.

(YANG Xiwu.Research on the Earth Pressure Theory and Reinforcement Load Reduction for the Culverts beneath High Fill [D].Chongqing：Chongqing University，2005. in Chinese)

[6]郑俊杰，马强，张军. 加筋减载涵洞的涵顶土压力计算[J]. 岩土工程学报，2011，33(7)：1135-1141.

(ZHENG Junjie，MA Qiang，ZHANG Jun.Calculation of Vertical Earth Pressure on Load Reduction Culverts under Embankments by Reinforcement [J]. Chinese Journal of Geotechnical Engineering，2011，33(7)：1135-1141. in Chinese)

[7]OKABAYASHI K, OHTANI W, AKIYAMA K, et al.Centrifugal Model Test for Reducing Earth Pressure on the Culvert by Using the Flexible Material[C]//Proceedings of the 4th International Offshore and Polar Engineering Conference.Osaka：International Society of Offshore and Polar Engineers，1994：620-624.

[8]SUN L，HOPKINS T，BECKHAM T.Stress Reduction by Ultra-Lightweight Geofoam for High Fill Culvert: Numerical Analysis[C]//Proceedings of the 13th Great Lakes Geotechnical and Geoenvironmental Conference.Milwaukee： American Society of Civil Engineers，2005：146-154.

[9]李盛，王起才，马莉，等.黄土地区高填土明洞土拱效应及土压力减载计算[J]. 岩石力学与工程学报，2014，33(5)：1055-1062.

(LI Sheng，WANG Qicai，MA Li，et al.Earth Pressure and Soil Arch Effect for High Fill Open Cut Tunnel in Loess Area under Different Load Reduction Schemes[J]. Chinese Journal of Geotechnical Engineering，2014，33(5)：1055-1062. in Chinese)

[10]李盛，王起才，马莉，等.高填土明洞土压力减载计算[J]. 华中科技大学学报：自然科学版，2013，41(11)：58-63.

(LI Sheng，WANG Qicai，MA Li，et al.Calculation Load Reduction of Earth Pressure on High Fill Open Cut Tunnel[J]. Journal of Huazhong University of Science and Technology：Natural Science，2013，41(11)：58-63. in Chinese)

[11]李盛，马莉，王起才，等.高填黄土明洞卸载结构土压力模型试验和数值模拟分析[J]. 岩土工程学报，2016，38(4)：636-642.

(LI Sheng，MA Li，WANG Qicai，et al.Model Tests and Numerical Simulations of Earth Pressure for Unloading Structures of High Fill Open Cut Tunnel[J]. Chinese Journal of Geotechnical Engineering, 2016，38(4)：636-642. in Chinese)

[12]姚振钢.建筑结构试验[M]. 武汉：武汉大学出版社，2001.

(YAO Zhengang. Building Structure Test[M]. Wuhan：Wuhan University Press，2001. in Chinese)

[13]马强.高填方涵洞受力特性及新型格栅减载方法研究[D]. 武汉：华中科技大学，2011.

(MA Qiang. Study on Stress Characteristics and Load Reduction by Triax Geogrid Reinforcement for High Embankment Culverts[D].Wuhan：Huazhong University of Science & Technology，2011.in Chinese)

[14]ZHENG J J，CHEN B G，LU Y E，et al.The Performance of an Embankment on Soft Ground Reinforced with Geosynthetics and Pile Walls[J]. Geosynthetics International， 2009 ，16 (3)：173-182.

[15]GIROUD J P.Determination of Geosynthetic Strain Due to Deflection[J]. Geosynthetics International，1995，2(3)：635-641.

[16]GIROUD J P. Designing with Geotextiles[J]. Materials and Structures, 1981，14(4)：257-272.

[17]李盛，马莉，王起才，等.高填明洞土压力计算方法及其影响因素研究[J]. 中国铁道科学，2016，37(5)：41-49.

(LI Sheng，MA Li ，WANG Qicai，et al. Calculation Method and Influencing Factors for Earth Pressure of High Fill Open-Cut Tunnel[J]. China Railway Science，2016，37(5)：41-49. in Chinese)