台阶式溢洪道相对流速变化规律研究

马世浩，刘韩生

（西北农林科技大学水利与建筑工程学院，陕西杨凌712100）

0 引 言

台阶式溢洪道作为一种高效的消能设施，在水利工程中得到了广泛的应用［1］。国内外工作者对台阶式溢洪道做了大量研究［2-6］，水力特性也是研究的热点，目前针对水力特性的研究主要集中在消能、压强等特性方面［7-11］。

流速是重要的水力参数，对其研究具有重要意义。吴宪生［12］推求了台阶式溢洪坝坝下流速，预测了空蚀破坏可能性；代仲海［13］模拟研究了台阶式溢洪道水流流态，得到了垂直于台阶坡度的法向方向上的流速分布；Boes 等［14］对坡度19°～55°台阶式溢洪道准均匀流段流速研究，并拟合了流速计算公式；张峰［15］通过数值模拟得到了流场内与剪切力相关的流速分布规律；WAN H［16］采用SPH方法对台阶断面的流速分布进行了数值模拟；刘应忠［17］引入相对摩阻流速的概念，研究了台阶式溢洪道摩阻流速在单宽流量、台阶高度、坡度影响下的沿程变化规律；马朋辉［18］将台阶式溢洪道与光滑式溢洪道进行对比分析，发现台阶式溢洪道流速变化复杂，规律性不强，不便应用。

杨吉健等［19，20］定义了相对流速，通过与光滑式溢洪道断面流速对比，研究了台阶式溢洪道过流断面平均流速在某一定性条件下的沿程变化规律。杨吉健等开辟了台阶式溢洪道流速研究的新思路，但其研究不够深入：①采用有因次数研究，反映的水流规律性不足；②没有总结相关系数与各参数之间的关系；③缺乏进一步的分析，例如没有研究线性规律的斜率是否有规律性。马朋辉［18］用x/L（L为台阶溢洪道流程长度、x为所处位置的流程长度）作为水流无因次参数，分析了滑行水流相对流速与无因次数之间的关系，得到了良好的相对流速沿程变化规律。虽然x/L为无因次数，但是它不够严谨，原因是：①该参数未经论证，而是直接使用；②从物理意义分析，该参数为相对流程，意味着水力参数，如流速、水深等与台阶式溢洪道长度有关，事实上，当流程超过一定程度后，水力参数保持常数，并不随流程变化而变化，这时水力参数与台阶式溢洪道长度无关。

本文进一步研究台阶式溢洪道流速变化规律，通过对台阶式溢洪道相对流速因次分析，定义相对临界水深与断面位置无因次数，并进行不同坡度的模型试验，分析相对流速与无因次数之间的函数关系，说明引入无因次数的必要性，得到台阶式溢洪道相对流速水力变化规律。

1 相对流速与无因次数的定义

1.1 相对流速的定义

台阶式溢洪道与对应光滑式溢洪道的示意图如图1 所示。台阶式溢洪道1-1 断面与光滑式溢洪道1′-1′断面互为对应断面。

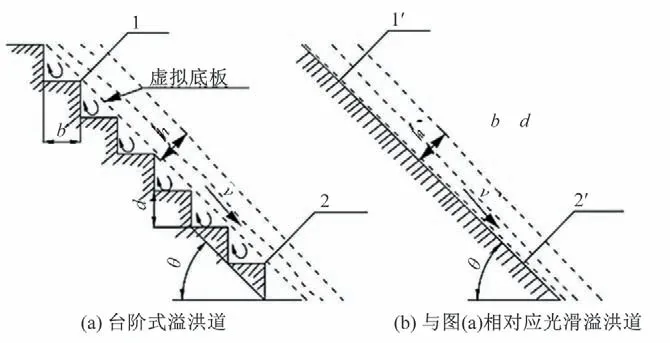
图1 溢洪道示意图Fig.1 Diagram of stepped spillways

根据定义［20］，过水断面某一位置处光滑式溢洪道断面平均流速与对应过水断面的台阶式溢洪道断面平均流速之差，为台阶式溢洪道相对流速：

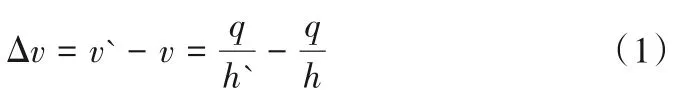
式中：v`为光滑式溢洪道断面平均流速，m/s；v为台阶式溢洪道断面平均流速，m/s；q为单宽流量，m3/s·m；h`为光滑式溢洪道断面平均水深，m：h为台阶式溢洪道断面平均水深，m；Δv为台阶式溢洪道相对流速，m/s。

台阶式溢洪道断面平均水深h在模型试验中通过多次探针测量取平均值，断面平均流速v通过实测流量值除以断面面积得到，台阶式溢洪道相对流速Δv通过以上参数计算即可求得。

光滑式溢洪道断面平均水深、平均流速可以根据溢洪道设计规范［21］求得。

1.2 无因次数的定义

根据相对流速的定义，相对流速与单宽流量、台阶高度、流程长度、坡度、重力加速度等有关，可表示为：

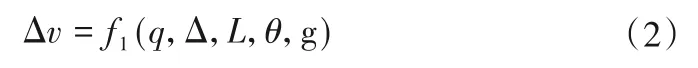
式中：Δ为台阶高度，m；L为流程长度，m；θ为坡度；g 为重力加速度，m/s2。

对式（2）相对流速进行因次分析，可得以下有关相对流速的无因次数群：

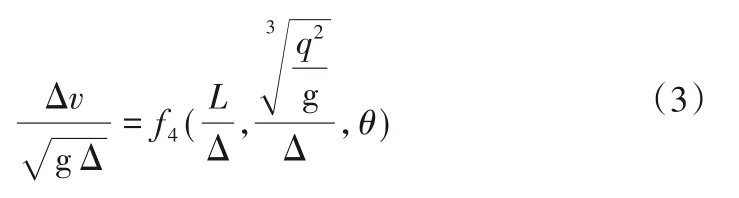
临界水深用来判断水流流态，光滑明渠临界水深为：

式中：hk为临界水深，m。

将式（4）带入式（3）可得：

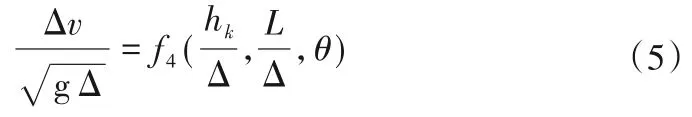
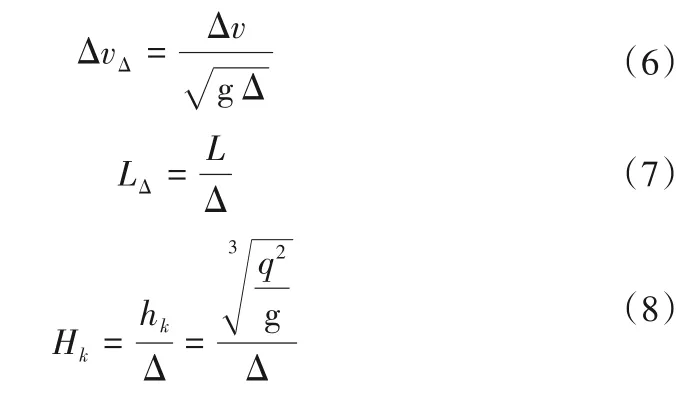
Hk是重要无因次参数，常用于判断台阶式溢洪道水流流态［22］，它是台阶式溢洪道和对应光滑式溢洪道的综合水力参数，既反映了台阶的影响，又反映了对应光滑式溢洪道水力特性的影响，本文用它可以揭示相对流速变化规律。

2 试验设计与水流流态

本文进行了五个不同坡度的台阶式溢洪道模型试验，且五个工程项目采用的消能方案均为“台阶式溢洪道+消力池”。五个坡度的模型试验基本资料见表1。

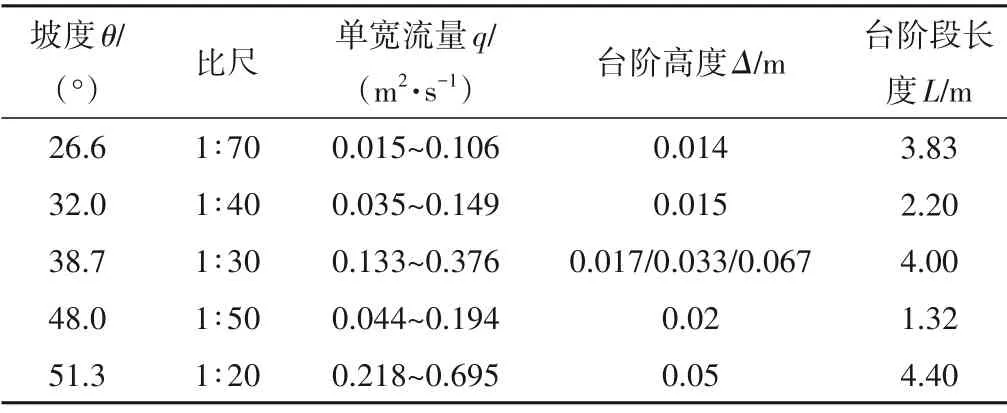
表1 试验基本资料Tab.1 Basic information of tests

5 个不同坡度的模型试验均按重力相似准则设计并进行，并采用不同模型比尺，模型布置图以坡度26.6°为例，如图2 所示。5 个坡度的模型共有7 种不同台阶式溢洪道体型，总共有42 组试验组次，对每个组次进行3 组流量的放水试验，测量溢洪道沿程断面水深，试验流量范围见表1。试验流量范围内台阶水流均为滑行水流，试验最小雷诺数值均大于500，即试验水流均为紊流。各断面水深通过有机玻璃透明边壁多次测量并取平均值，台阶式溢洪道水深测量如图3所示，以台阶阶顶连线为基准，在各阶顶处垂直于基准线测量断面水深，过流流量采用矩形薄壁堰和三角堰量测。

图2 26.6°模型布置图Fig.2 26.6°model layout

图3 水深测量示意图Fig.3 Water depth measurement in stepped spillway

3 相对流速变化规律

3.1 相对流速与断面位置无因次数的关系

台阶式溢洪道相对台阶流速ΔvΔ与断面位置无因次数LΔ的关系如图4～8 所示，可见，无论Hk、θ如何变化，两者之间均呈现线性关系，相关系数变化情况见表2，相关系数较高，为0.985 5～0.999 6，说明线性关系良好。台阶式溢洪道阶相对台阶流速沿断面位置无因次数线性递增，这是由于台阶式溢洪道设置了等高、均匀的台阶，而台阶式溢洪道沿程各台阶对水流流速的阻碍作用是相同的，台阶式溢洪道某一断面的相对台阶流速实际上是前面单个台阶对水流流速的阻碍作用之和。相对台阶流速与断面位置无因次数之间的关系可表示为：

式中：k为线性关系的斜率。

上式适用条件为坡度26.6°～51.3°，相对临界水深1.83～12.1。

斜率k是无因次数，它反映了相对台阶流速ΔvΔ与断面位置无因次数LΔ之间的关系，即断面位置无因次数对相对流速的影响可用k表示，k的影响因素为Hk、θ。

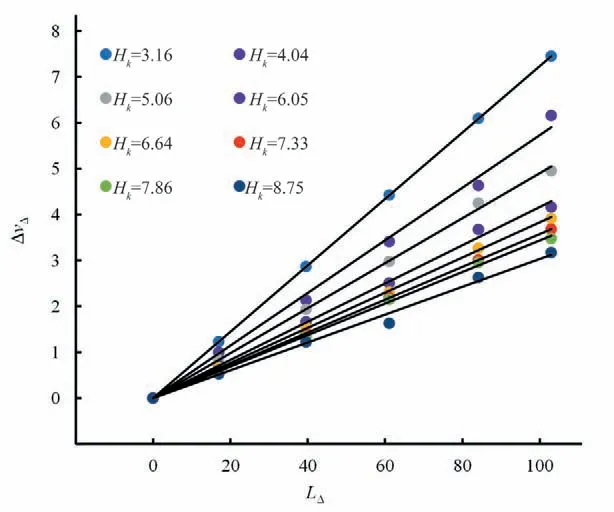
图5 θ=32°时ΔvΔ ～LΔ 关系Fig.5 Relation of ΔvΔ～LΔ at θ=32°

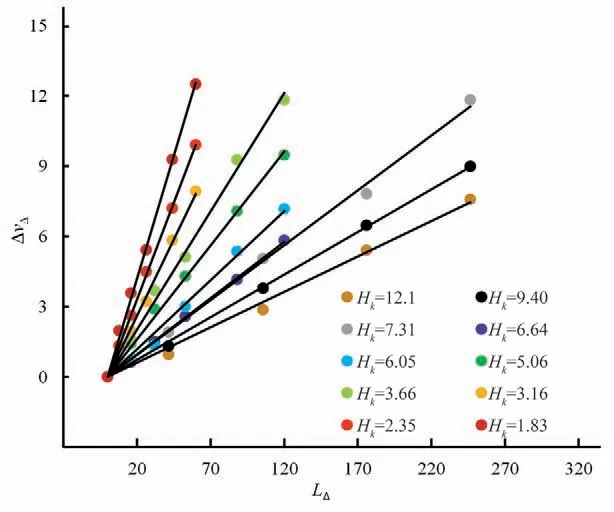
图6 θ=38.6°时ΔvΔ ～LΔ 关系Fig.6 Relation of ΔvΔ～LΔ at θ=38.6°

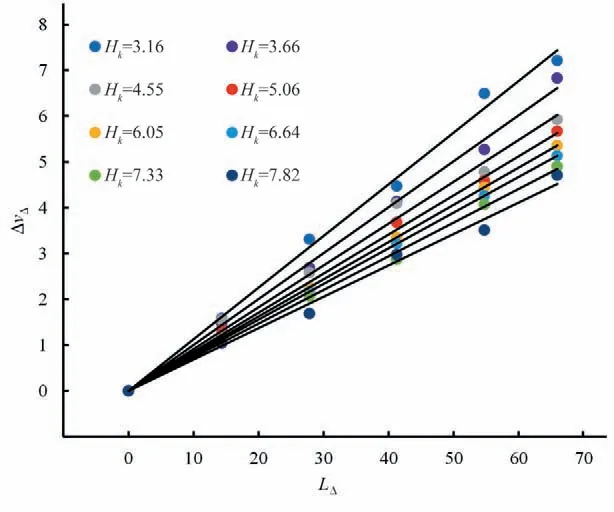
图7 θ=48°时ΔvΔ ～LΔ 关系Fig.7 Relation of ΔvΔ～LΔ at θ=48°

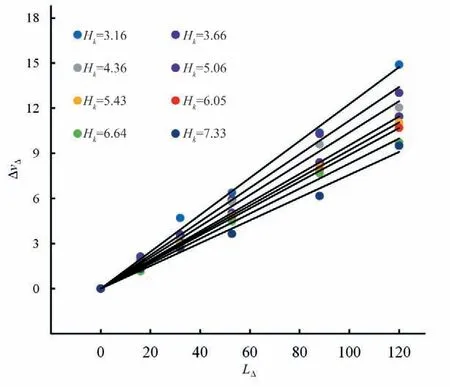
图8 θ=51.3°时ΔvΔ ～LΔ 关系Fig.8 Relation of ΔvΔ ～LΔ at θ=51.3°

3.2 相关系数与坡度、相对临界水深的关系

根据表2，可以计算出各个坡度、相对临界水深的相关系数均值，列于表3、4。可得不同坡度、相对临界水深与相关系数的均值在0.993 9～0.998 6之间，均值较高且变化很小，说明各直线相关系数较高，线性关系良好；标准差则表示了相关系数的波动范围，表中标准差在0.002 76～0.004 26 之间，说明随着坡度、相对临界水深的变化相关系数波动值很小，相对于相关系数来说基本可以忽略。不论Hk、θ如何变化，ΔvΔ与LΔ保持着较高的相关性。

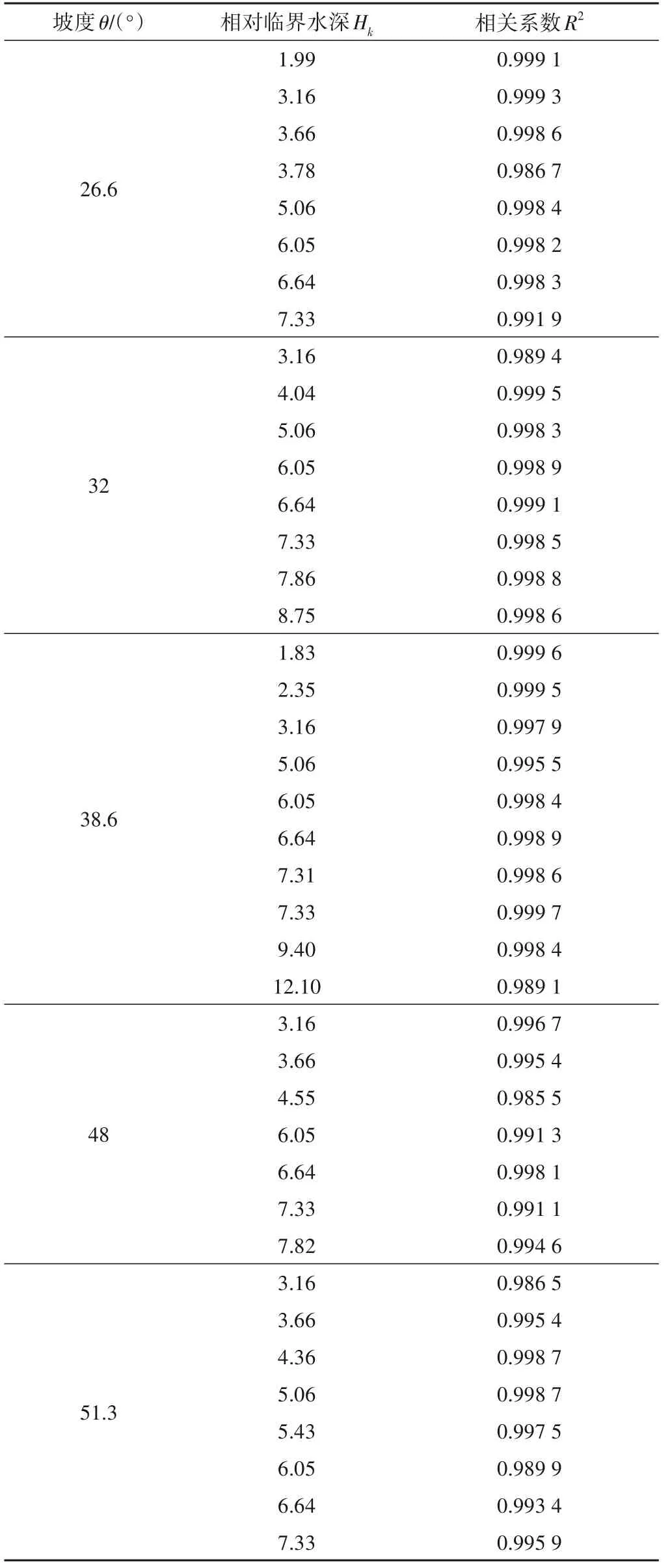
表2 相关系数表Tab.2 Correlation coefficient table

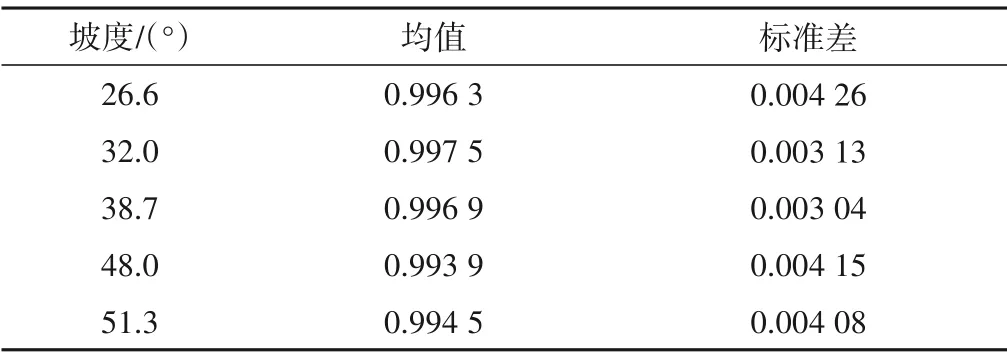
表3 相关系数与坡度的关系Tab.3 Relationship between correlation coefficient and slope

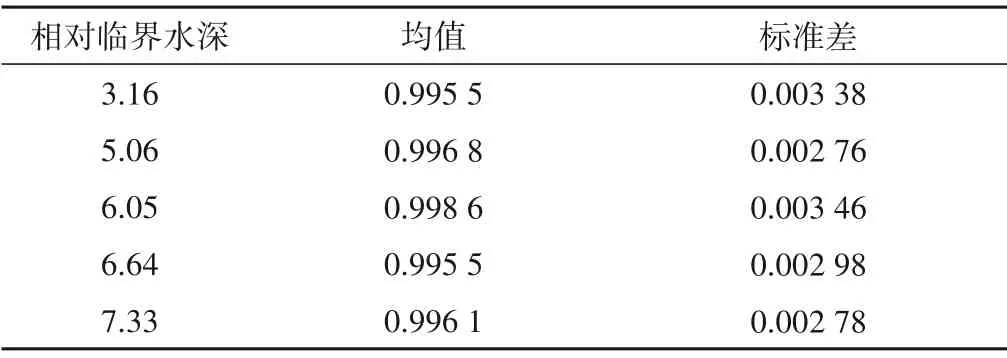
表4 相关系数与相对临界水深的关系Tab.4 Relationship between correlation coefficient and relative critical water depth

3.3 斜率变化规律

3.3.1 斜率与相对临界水深的关系

ΔvΔ与LΔ的线性斜率k与相对临界水深Hk的关系如图9 所示，不同坡度下斜率与相对临界水深呈幂函数递减关系，斜率随着相对临界水深的增大逐渐减小，相关系数为0.982 7～0.994 8，相关性良好。斜率与相对临界水深呈幂函数关系，说明相对台阶流速随相对临界水深的增大而减小，根据相对临界水深的定义可知，适当增加台阶高度对水流能量的耗散有利。

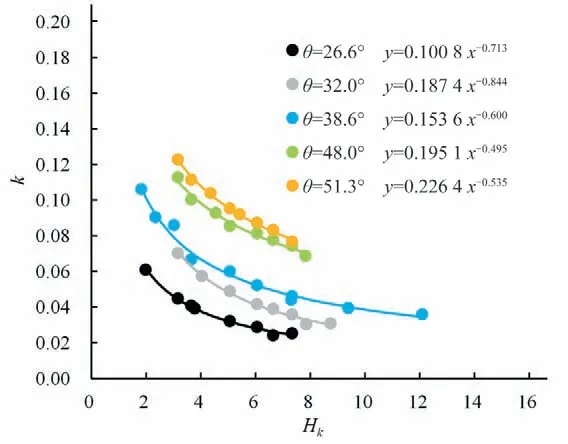
图9 斜率与相对临界水深的关系Fig.9 The relationship between the linear slope and the relative critical water depth

3.3.2 斜率与坡度的关系

斜率k与坡度θ的关系如图10所示，可见，不同相对临界水深情况下斜率与坡度呈线性递增关系，相关系数为0.985 7～0.993 5，相关性较高。斜率随着坡度的增大而增大，说明相对台阶流速随坡度的增大而增大，则适当的增加坡度更有利于溢洪道的消能。

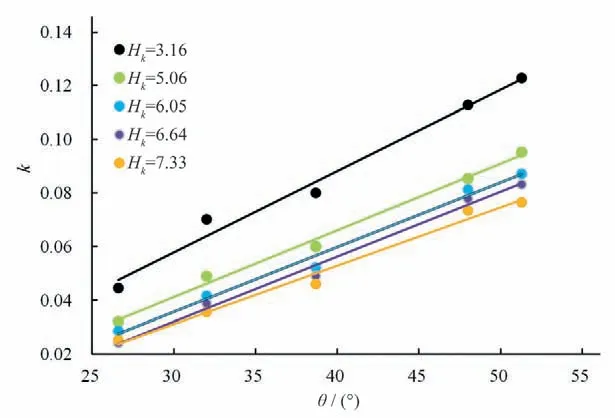
图10 斜率与坡度的关系Fig.10 The relationship between the linear slope and slope

3.3.3 斜率与相对临界水深、坡度的关系

根据图9、10所表达的规律，可以拟合出斜率与相对临界水深、坡度之间的关系，曲面拟合结果如图11 所示。图11 中也能反映上述斜率与相对临界水深、坡度之间的变化关系。台阶式溢洪道相对流速指台阶的影响使某一断面水流流速相对于同体型光滑溢洪道对应断面流速的减小值，因此可以得出台阶对水流流速的阻碍作用在量值上随相对临界水深的增大而减小，随坡度的增大而增大。

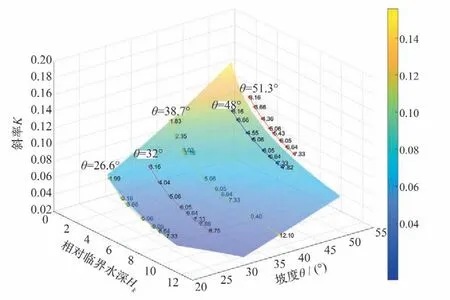
图11 斜率、相对临界水深、坡度的关系Fig.11 The relationship between the linear slope，the relative critical water depth and slope

曲面公式为：

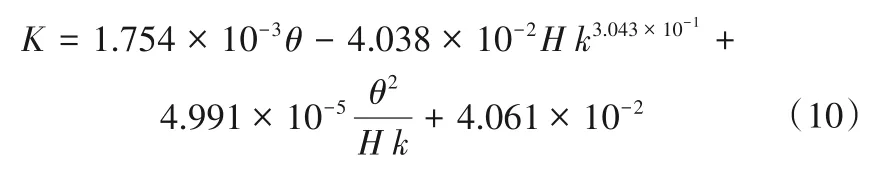
此公式适用范围为坡度26.6°～51.3°、相对临界水深1.83～12.1，相关系数为0.989 9，相关性良好。

4 应用实例

研究台阶式溢洪道相对水力特性的最终目的是为了更好地了解和应用台阶式溢洪道，鉴于台阶式溢洪道相对流速所呈现的较强的规律性及光滑溢洪道水力计算理论的成熟性，可以利用相对流速规律计算水面线、消能率等水力参数，为台阶式溢洪道水力计算提供了新方法。现以水面线计算为例：

坡度48°，单宽流量30.4 m2/s，台阶高度1.0 m台阶溢洪道长度65.94 m，计算台阶式溢洪道滑行水流水面线。

计算过程如下：

由式（8）计算得Hk=4.55，符合相对流速公式（9）、斜率经验公式（10）的应用条件。

（1）首先根据式（10）计算出斜率k=0.091 53；

（2）将k=0.107 04 代入式（9）和式（6）得到相对台阶流速ΔvΔ和相对流速Δv；

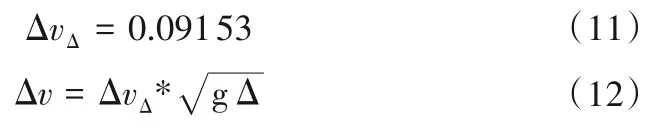
（3）依据溢洪道设计规范，采用能量方程、连续性方程，用分段求和法［22］即可得到光滑式溢洪道水深、流速；

（4）根据相对流速、光滑式溢洪道流速，可根据式（1）求得台阶式溢洪道流速v：

（5）最后由台阶式溢洪道流速即可得到台阶式溢洪道水深h：

计算过程见表5。

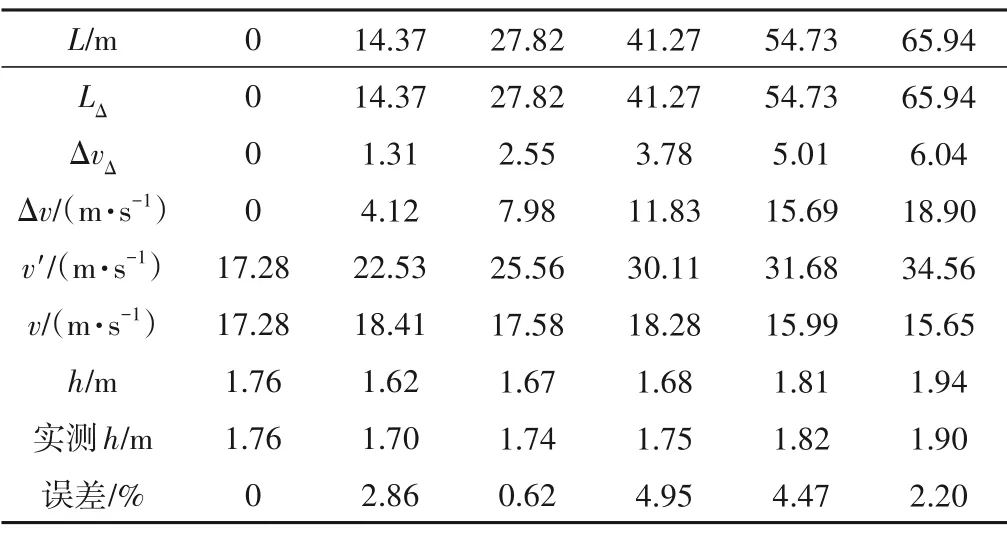
表5 水面线计算过程Tab.5 Calculation process of water surface line

表5 中同时列出了模型实测值和误差（模型布置图如图12所示，模型按重力相似准则设计，模型比尺为1∶50）。可见计算值与试验值误差不大于5%，显然，根据相对流速的规律可以较为准确地求得水面线。

图12 48°模型布置图Fig.12 48°model layout

5 结 语

对相对流速进行研究，得到以下结论。

（1）通过因次分析，得到相对台阶流速及与其相关的3个无因次数：断面位置无因次数、相对临界水深、坡度。

（2）依据5 个坡度、7 个台阶高度的42 组模型试验资料，表明相对台阶流速沿断面位置无因次数呈线性增大变化。

（3）对线性关系的相关系数进行分析，说明不论相对临界水深、坡度如何变化，相对台阶流速与断面位置无因次数始终保持着较高相关性。

（4）线性关系的斜率与相对临界水深呈幂函数递减关系，说明相对台阶流速随相对临界水深的增大而减小，则相对临界水深越大台阶对水流的阻碍作用越小；与坡度呈线性递增关系，说明相对台阶流速随坡度的增大而增大，则坡度越大台阶对水流的阻碍作用越大。所以适当增加台阶高度、坡度对消能更有利；在小单宽流量、坡度较陡时更有必要采用台阶式溢洪道。并通过曲面拟合得到斜率关于相对临界水深和坡度的经验公式。

（5）利用相对流速良好的规律性可以进行水面线、消能率等水力计算，为台阶式溢洪道水利计算提供新方法。以水面线计算为例，结果表明可以比较准确的计算台阶式溢洪道水面线。

将台阶式溢洪道和对应光滑溢洪道对比分析，得到台阶式溢洪道相对流速变化规律，该规律相对于常规研究方法有明显优势，总结该规律对于认清台阶的存在对水流的改变具有重要意义，且对台阶式溢洪道复杂的水力计算有很大帮助。 □