灯泡贯流式水轮机固液两相定常流动数值模拟
2021-11-29葛新峰蔡建国王金亮
葛新峰,张 敬,蔡建国,王金亮,赵 雷,张 雷,李 丽,郑 源
(1.河海大学能源与电气学院,南京210098;2.重庆航运建设发展有限公司,重庆500000;3.黄河万家寨水利枢纽有限公司,山西偏关036412;4.黄河水利科学研究院,郑州450003)
0 引 言
我国许多河流都有较大的含沙量,西北地区尤甚,每当季风或汛期,河流的含沙量就会增加。因此,河流中挟带的泥沙不可避免的会对电站运行产生不利影响。早在1984年,Tiloth水电站就出现了较为严重的泥沙磨损问题,引起了学者们的重视和研究[1]。2003年投产的Nathpa Jhakri电站,在运行几年后,就遭遇了严重的泥沙磨损问题,之后经过多年的实践经验和专家意见才使得此问题得以控制[2]。截至2004年,尼泊尔运行的19 座电站,几乎无一例外的受到了泥沙侵蚀的困扰,当地政府不得不面对巨大的维护成本和系统效率的下降[3]。在我国,小浪底、刘家峡电站因河流携沙量大,过流部件遭到了严重的磨损,三门峡更是由于泥沙问题,致使机组效率下降高达10%[4-6]。在此背景下,展开关于水力机组的固液两相流研究具有重要意义。
目前,对于水力机械固液两相流的研究,多集中在水泵和混流式水轮机上[7-10],有关贯流式水力机组两相流的研究还较为缺乏。B Thapa 认为泥沙对水电站的影响主要集中在两个方面:泥沙的沉积对电站高效运行的影响,以及泥沙沉积物通过过流部件时对其造成的磨蚀[3]。G R Desale 等人通过对不同类型的水力机械进行研究,总结出泥沙对水力机械的影响因素主要体现在泥沙的硬度、形状、浓度、粒径大小,此外,还与材料性质、运行条件、流速、冲击角等因素有关[11-14]。M K Padhy 总结了大量国内外研究文献,得出泥沙磨损会导致叶片型线改变、机组振动增加、部件疲劳破坏以及运行效率降低[15]。刘文俊等人研究了固液两相流下贯流式机组导叶内部流场和压力场的分布[16]。闵广鹤应用多相流模型对贯流式水轮机内流场的固液两相流进行模拟计算,在固、液两相的体积分数图和速度分布图的基础上分析了空蚀和泥沙磨损[17]。张家荣对贯流式机组的灯泡体、活动导叶、转轮及尾水管表面进行了泥沙磨损及泥沙颗粒流动分析,研究了泥沙颗粒直径对上述过流部件磨损位置和磨损程度的关系[18]。彭笙洋等人基于Particle 和非均相模型,对贯流式水轮机内部流场进行了数值模拟,分析了不同泥沙粒径下过流部件工作面和背面的固体颗粒相的滑移速度及固相体积分数[19]。
本文在前人研究的基础上,选用Euler-Euler 模型对灯泡贯流式机组的固液两相流进行定常计算。对比了清水工况和固液两相流工况的外特性和流动特性,并且深入分析了颗粒物性参数对机组定常流动特性的影响。在此基础上,提出了灯泡贯流式水轮机在检修时应重点关注的泥沙磨损部位,为机组的检修、安全运行提供参考。
1 计算方法
1.1 多相流模型
模拟多相流时所用的连续介质模型一般分为Euler-La⁃grange 模型和Euler-Euler 模型[20-23]。Euler-Lagrange 模型的连续相和离散相分别用欧拉法和拉格朗日法求解,包括颗粒轨道模型和DEM模型,离散相需要单独计算。Euler-Euler模型的连续相与离散相均用欧拉法求解,连续相与离散相同时用N-S 方程计算,不需要对离散相再进行单独计算,适用于颗粒拟流体的两相流模型。本文选用Euler-Euler 双流体模型中的Euler 模型对灯泡贯流式机组的水沙两相流进行求解。求解的控制方程组如下:
液相质量守恒方程:
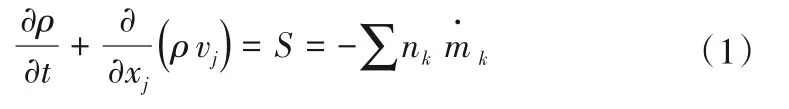
固相质量守恒方程:
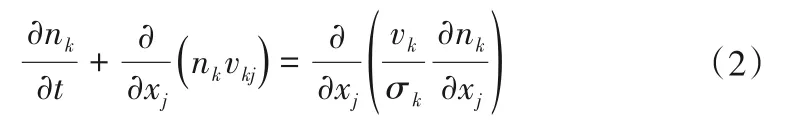
液相N-S方程:
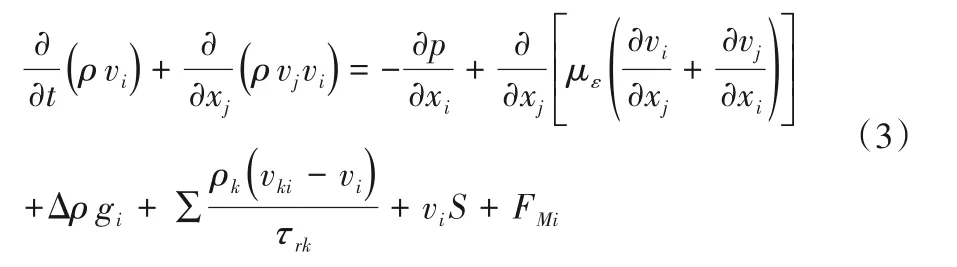
固相N-S方程:
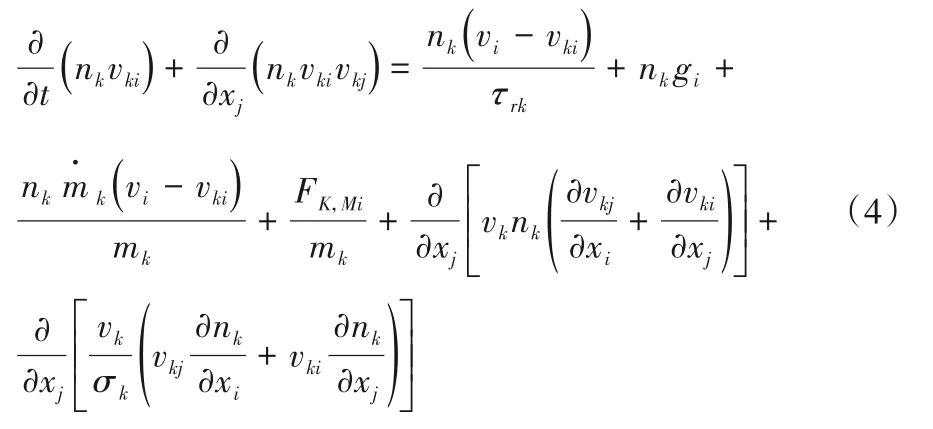
液相能量方程:
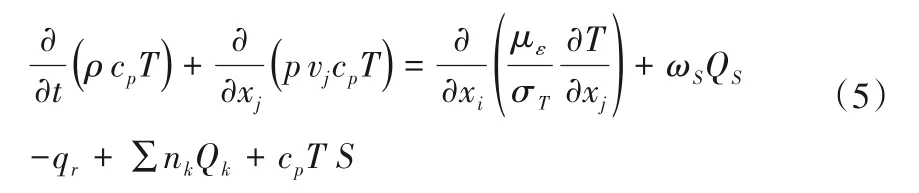
固相能量方程:
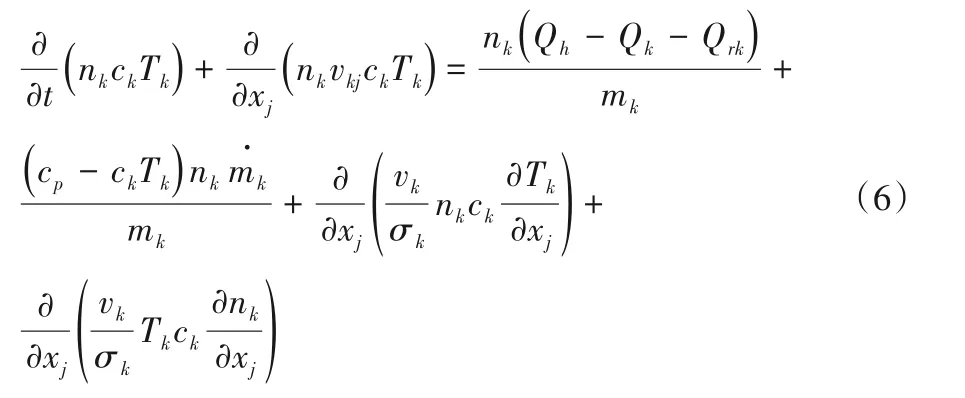
两相流组分方程:
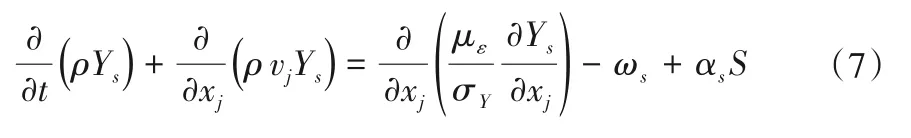
式中:ρ为流体介质密度;t为时间;v为速度矢量;P是介质压力;c为比热容;T为温度;Q为流量;τ为作用微元体表面上的黏性力;m,n为单位向量;i,j,k为指标符号;με为流体的黏性系数;σk为应力张量。
1.2 模型建立及网格划分
灯泡贯流式水轮机流道三维模型如图1 所示,共分为进水流道、灯泡体、导叶段、转轮段和尾水管几个部分,采用ICEM 软件对流体计算域进行网格划分,由于机组结构复杂,故采用自适应性较好的非结构化网格进行划分,并对关键部位进行局部加密。对网格的无关性进行验证时,在额定工况下,对网格的5种划分方案(440、480、520、560、600 万网格数)进行计算,可得到网格数量与机组效率的关系,如图2所示,随着网格总数的增加,机组效率的增加逐渐变缓,本文选用560万个的网格。
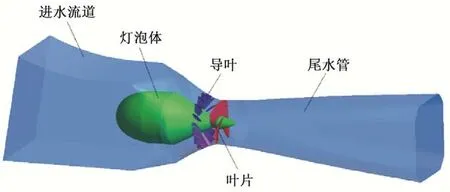
图1 灯泡贯流式水轮机组模型图Fig.1 Bulb Tubular Turbine Model Diagram
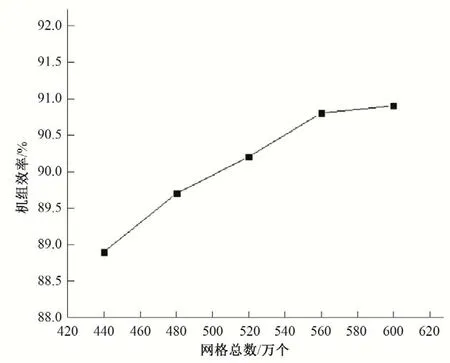
图2 网格无关性验证Fig.2 Grid independence verification
1.3 计算假设及边界条件
在进行固液两相流计算时,做出的假设有以下3点:①主相为清水,第二相为单一的固体颗粒;②离散的固体颗粒相是粒径均匀的球形,且计算时不产生相变;③液相和固相都视为连续、不可压缩的,其温度等物理特性看做是常数。
湍流计算模型为RNG k-ε模型,30<y+<100,可以保证网格计算时的y+值满足要求,计算精度设置为10-5,收敛条件为计算水头和效率的幅值不超过1%,在定常计算中,将动静部件的交界面设置为冻结转子类型。边界条件设置如下:进口边界选用压力进口,流量出流边界。壁面设置为绝热无滑移壁面。
1.4 计算工况
清水计算工况为Case0,浑水工况以Case2[1%,2 600,0.1](泥沙浓度CV=1%,密度ρ=2 600 kg/m3,泥沙颗粒直径Dp=0.1 mm)为研究基本工况,采用控制变量法研究泥沙颗粒物性参数对机组外特性及流动特性的影响。
在Case2 基础上,密度ρ分别取2 400,2 600,2 800 和3 000 kg/m3,研究泥沙密度的影响;泥沙浓度CV分别取0.5%,1%,2%和5%,研究泥沙浓度的影响;泥沙颗粒直径Dp分别取0.05,0.1,0.2 和0.5 mm,研究泥沙径粒的影响,文中所有计算工况如表1。

表1 计算工况及参数[CV,ρ,Dp]Tab.1 Calculation conditions and parameters[CV,ρ,Dp]
2 结果分析
2.1 清水工况case0 与两相流工况case2 的外特性与流动特性对比
清水中加入泥沙后,泥沙的物性参数设置如下:密度取2 600 kg/m3,体积分数取1%,泥沙直径设置为0.1 mm。如表2所示,为水流含沙前后的外特性对比。可以看出,水流在含沙后,其计算效率与机组出力都有一定程度的下降,本文计算结果的规律和文献[24]一致,随着流量的增大,空化区域是先增大后减小的,所以在大流量工况下,出力有一定的上升是可能存在的。但在合适的流量范围内,总体上可以说泥沙的存在会使空化区域增大,从而降低机组的出力和效率。图3 展示的是水流含沙前后X=0 m 截面处的流线压力图,可以看出:只有清水存在时,流线均匀而顺畅;加入泥沙颗粒后,整体流态变差,水流与进水口不再垂直,进水流道底部出现了大面积回流和旋涡,尾水管中的旋涡随着水流推进而增大,水流的湍动能也随之增加。水流含沙后,一方面,泥沙颗粒改变了流线走向,颗粒在流经机组时会与过流部件表面产生撞击,造成水力损失,如图4 所示,可以看到,在颗粒相的扰动下,导叶和转轮的进口处产生了明显的撞击角;另一方面,泥沙颗粒引起的涡流耗散了大量水能,亦导致了水力损失的增加。在二者的共同作用下,造成了如表2所示的效率和出力下降。
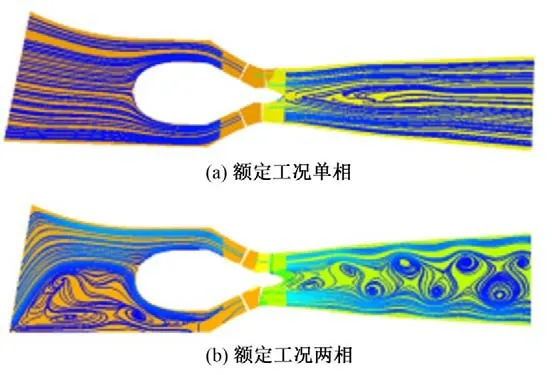
图3 不同物相工况下X=0 m的截面流线压力图Fig.3 Cross-sectional streamline pressure diagram of X=0 m under different phase conditions
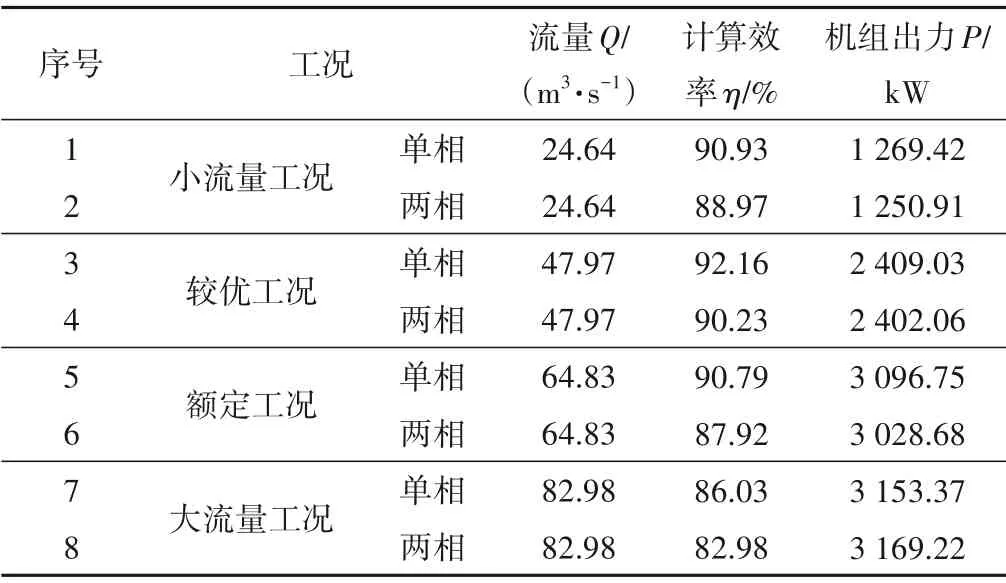
表2 单相、两相时水轮机组外特性Tab.2 External characteristics of hydraulic turbine unit in single-phase and two-phase
2.2 泥沙分布特性
2.2.1 流道内泥沙分布特性
如图5,为不同泥沙颗粒物性参数下的流道底面颗粒分布云图。可以看出,不管在哪种条件下,进口流道底面的泥沙颗粒含量都高于尾水管底面的泥沙颗粒含量。随着泥沙颗粒密度的增加,进口流道至导叶过渡段的泥沙磨损越来越严重;随着泥沙浓度的增加,进口流道的泥沙分布越来越不均匀,且泥沙集中位置由流道进口向进口流道至导叶的过渡段逐渐后移;随着泥沙颗粒直径的增加,相同体积颗粒的质量增大,受重力影响,颗粒在流动时逐渐沉降,当直径增大到0.2 mm 及其以上时,进水流道底面基本全部被泥沙覆盖,且有向转轮部位延伸的趋势,与此同时,尾水管段泥沙分布也越来越不均匀,沉积情况越来越严重。因此,对于灯泡贯流式水轮机组的泥沙清淤工作,应重点关注进口流道底面及进口流道至导叶的过渡段。
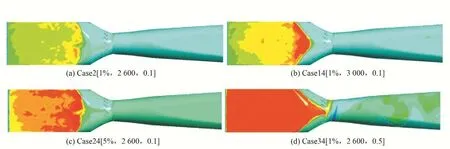
图5 不同泥沙颗粒物性参数下的流道底面颗粒分布云图Fig.5 Cloud chart of particle distribution on the bottom surface of the flow channel under different sediment particle physical parameters
2.2.2 轮毂及叶片表面的固体颗粒分布云图
图6 和图7 显示的是不同泥沙物性参数下轮毂及叶片正面和背面表面的固体颗粒分布云图。由图可知,不同物性参数下,叶片和轮毂表面泥沙分布的共同点如下:叶片正背面和轮毂表面的颗粒分布并不均匀;叶片进水边头部位置处的泥沙分布最多,磨损最严重,这是因为叶片头部靠近水流进口,颗粒随水流撞击叶片后动量逐渐损失,主要分布在叶片头部;叶片表面固体体积分数分布规律沿圆周方向大致呈周期性;叶片正面泥沙分布的体积分数均大于叶片背面。
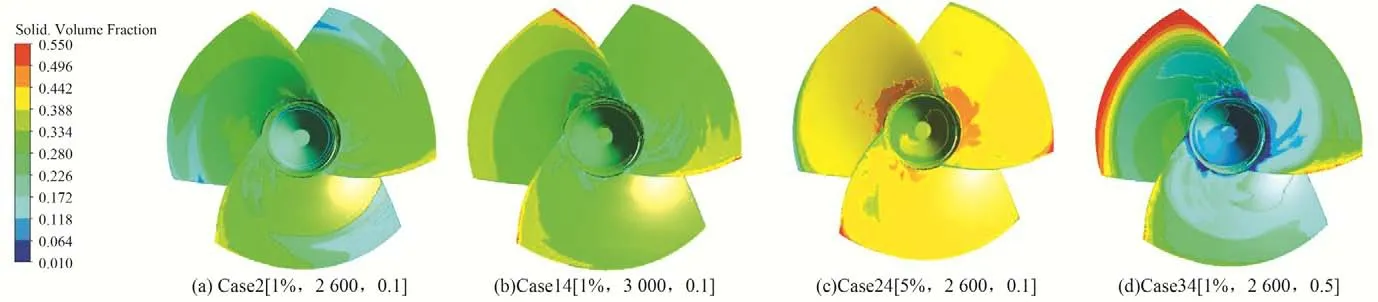
图6 不同泥沙物性参数下叶片正面Fig.6 The front of the blade under different sediment physical parameters
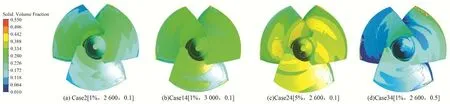
图7 不同泥沙物性参数下叶片背面Fig.7 The back of the blade under different sediment physical parameters
不同的是,随着固体颗粒密度的增加,叶片表面和轮毂处的泥沙含量虽然也逐渐增加,但泥沙体积分数从进水侧至出水侧、从轮毂处至轮缘处逐渐减小,大致规律并没有改变,因为密度增加后,相同体积内的固相具有更大的惯性力,再加上旋转离心力的作用,颗粒随水流流动后滞留在轮缘处,所以轮缘处泥沙含量较高。随着泥沙浓度的增加,叶片正、背面的泥沙体积分数也随之增加,且叶片正面的泥沙分布有从轮缘向轮毂推进的趋势。随着泥沙直径的增大,叶片和轮毂表面的固体体积分数均逐渐增大,叶片正、背面的泥沙含量差距也逐渐增大,这是因为颗粒直径增大后,水流裹挟着的颗粒具有更大的质量流量,惯性力随之增强,泥沙含量较高区域逐渐移动至轮缘处,并滞留其上。
因此,泥沙颗粒密度、浓度、直径的增加,都会加重泥沙颗粒对叶片表面的磨损,尤其是叶片正面进水边和轮缘处,影响转轮的输出力矩,并缩短了检修周期和叶片的使用寿命。
2.3 叶片表面静压沿弧长方向的分布情况
图8为不同泥沙物性参数下翼型中间径向位置叶片表面静压沿弧长方向的分布情况。由图可知,当水流含沙时,叶片进水侧背面会有较为明显的脱流现象,这使得叶片头部的空化性能变差,且由于回流等现象的存在,叶片正面尾部存在压力相对较低的区域。当颗粒密度增加时,叶片正面压力变化不大,叶片背面压力逐渐变大,说明叶片正背面压差随颗粒密度的增加而减小,同时叶片的输出力矩也会减小。随着颗粒进口浓度的增加,叶片正、背面压力均略有增大,其中,当颗粒浓度由0.5%增大至1%时,不同径向位置处叶片背面压力均明显增大,而当浓度超过1%时,叶片背面的压力变化幅度较小。故颗粒进口浓度的增加,也会使叶片正背面压差逐渐减小。当固体颗粒直径逐渐变大时,不同径向位置处叶片正面和背面的压力变化均较小,颗粒直径的变化对叶片正背面压差影响较小。
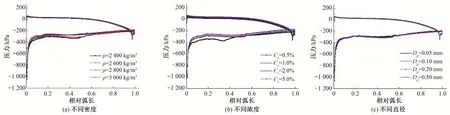
图8 不同泥沙物性参数下叶片表面静压分布曲线(span=0.50)Fig.8 Distribution curve of static pressure on blade surface under different sediment physical parameters
2.4 泥沙物性参数对机组外特性的影响
如图9 所示,为机组外特性随泥沙物性参数的变化曲线。泥沙的颗粒密度、颗粒浓度以及颗粒直径增加时,机组的效率和出力都会随之下降。究其原因,是因为当泥沙的密度、浓度、直径增加时,对流场的扰动作用也在增加,随之产生的涡流耗散与撞击损失也会进一步加大,从而造成水力效率下降、出力减少。
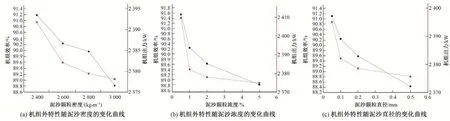
图9 机组外特性随泥沙物性的变化曲线Fig.9 The change curve of the external characteristics of the unit with the physical properties of the sediment
3 结 论
本文采用Euler-Euler 模型对灯泡贯流式机组的固液两相流进行了定常计算。对比了清水工况和固液两相流工况下的外特性和流动特性,分析了颗粒物性参数对机组运行特性及对不同过流部件的泥沙浓度分布特性,为机组的检修提供了一定的参考依据。主要结论如下:
(1)加入颗粒相后,颗粒对水流会有很明显的扰动作用。此时,导叶和转轮进口处均产生了明显的撞击角,且由泥沙颗粒引起的旋涡耗散了部分水能。这导致了水力损失的增加,机组效率和出力的下降。
(2)受重力的影响,贯流式水轮机流道中,进口流道的泥沙分布浓度比出口相对高,特别是为进口流道底面,随着泥沙径粒、浓度、密度的增加,这些泥沙浓度高的地方可能会发生磨损。
(3)当固体颗粒直径逐渐变大时,叶片正面和背面的压力变化均较小,颗粒直径的变化对叶片正背面压差影响较小。 □
