多种水轮机模型的仿真对比分析

陈 上，陈金保，王安林，丘涛基，陈齐灯，肖志怀

（1.武汉大学动力与机械学院，武汉430072；2.福建华电金湖电力有限公司，福建三明353399）

0 引 言

随着大规模风能、太阳能等新能源电能的接入，输电电网架构和区域电网间互联方式日趋复杂，在电力系统的规划、调峰、安全备用、频率电压稳定等方面带来更多新的问题。作为电网中起主要调节作用的水电站，对其调节性能提出了更高要求。由于水轮机内部流体运动复杂，各运行变量间的动态关系复杂、耦合程度高，难以用简单的数学模型描述，目前只能通过真机试验、模型试验和近似解析方法来建立水轮机模型。在工程上通常采用稳态特性近似代替动态特性建立水轮机模型［1］，进而对水轮机的稳态特性、动态特性、控制策略等进行研究。水轮机建模主要包括外特性法［2-6］和内特性法［7-9］，内特性建模由于过度依赖水轮机几何参数和结构参数，且实际建模时很难获得具体准确的参数，故很少采用。外特性建模主要基于模型运转综合特性曲线（或原型运转综合特性曲线），位于模型综合特性曲线内的工况通常可较好表达，但小开度区间建模还需要进一步深入研究；此外，也有学者提出其他水轮机建模方法，如适用于电力系统仿真的递推水轮机线性模型［10］；反映系统能量特性的非线性水轮机哈密尔顿模型［11］。为了分析各类模型之间的建模精度与差异，为水轮机建模提供理论指导，本文结合目前常用的分段线性化模型、理想水轮机模型、神经网络模型和插值法模型，借助matlab 仿真平台，针对实际机组开展仿真建模研究，对比分析不同建模方法在稳态特性、动态特性、建模复杂程度、模型仿真时间等方面效果与差异。

1 水轮机建模原理

1.1 分段线性化模型

水轮机动态特性通常使用水轮机稳态工况下的力矩与流量特性表示，其非线性稳态表达式为式（1）和式（2）：

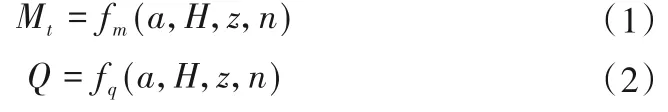
式中：Mt为水轮机力矩；a为导叶开度；H为水轮机水头；z为桨叶角度；n为机组转速；Q为水轮机流量。

将这两个式子展开为泰勒级数并略去二次及以上高次项得式（3）与（4）。

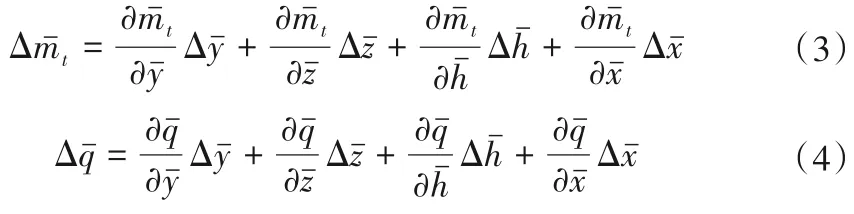
为方便描述，将其偏导数替换成传递系数，如式（5）：

该方程描述稳态工况附近微小偏差时力矩和流量的变化。即该方程的应用条件是已知该工况的传递系数，且波动幅度在工程允许范围之内。当工况波动过大时，该方程计算数据会与实际结果产生较大的误差，故当波动较大时，此方法应用受到限制。

分段线性化建模中，关键是工况的划分和传递系数的计算。工况划分通常以水头和导叶开度等比例选取，工况划分越细，模型精度越高。

传递系数计算通常采用两点法或者曲线拟合法，适合计算有限工况点的传递系数，但计算繁琐，难以清晰全面认识传递系数随工况变化规律，故而出现通过模型综合特性曲线结合BP神经网络对数据处理后直接进行求偏导数的处理方法，此方法计算既保证了计算精度又减少了计算量［12］。

计算传递系数，得出如图1 所示的水轮机分段线性化模型方框图［13］，图1中Tw为水流惯性时间常数。

1.2 理想水轮机模型

主要分析调节系统其他环节时，一般采用理想水轮机模型表示水轮机特性。理想水轮机模型是对1.1 节分段线性化模型进行简化，应用时不考虑桨叶角度，通过桨叶角度与导叶开度协联，将转浆式水轮机视为混流式水轮机，考虑到转速对力矩和流量影响较小，理想水轮机模型中传递系数ex和eqx取为0，在额定工况附近，取ey=1.0，eh=1.5，eqy=1.0，eqh=0.5，将传递系数合并得到传递函数如图2所示。

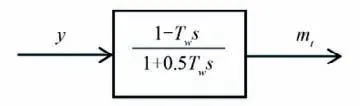
图2 理想水轮机模型Fig.2 Ideal hydraulic turbine model

1.3 神经网络模型

随着人工智能发展，基于神经网络技术的非线性建模技术得到广泛应用。针对BP 神经网络，只要有足够多隐含层和隐含层节点，就可以逼近任意非线性映射关系，许多学者将神经网络引入水轮机建模之中［14-17］。

实时仿真中，利用神经网络实现水轮机非线性特性计算具有计算简单、精度可控且导数连续等优点。可供选择的神经网络很多，如前馈神经网络、循环网络和对称连接网络等，水轮机建模中使用前馈神经网络中BP 神经网络较多，其网络结构如图3所示。

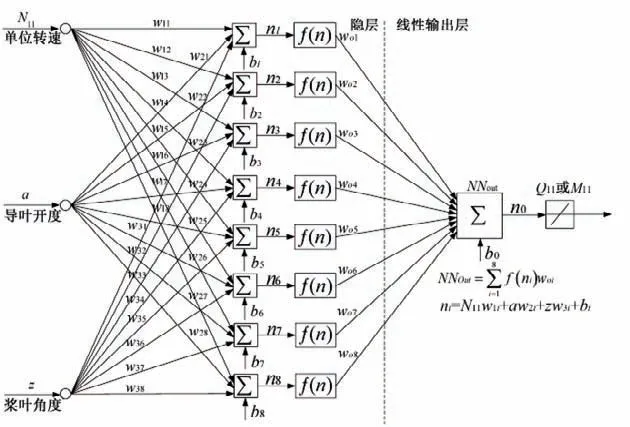
图3 BP神经网络结构图Fig.3 BP neural network structure diagram

该网络包含三输入、单输出和一个隐层，实现轴流转浆式机组流量或力矩模拟，其隐层神经元个数可调整，输出层为线性，隐层神经元传递函数为log-signoid 函数。神经网络算法表达式如式（6）：

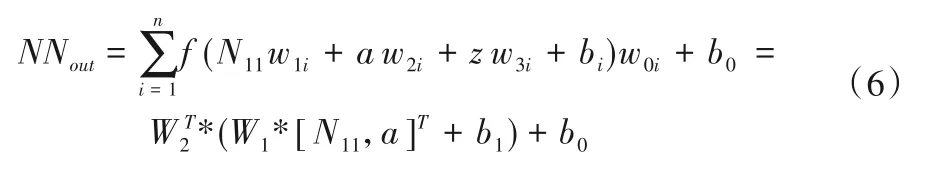
式中：NNout为神经网络输出；N11为单位转速，w1i、w2i、w3i为隐层神经元权值；bi为隐层神经元阈值；w0i为输出层权值；b0为输出层阈值；W1、W2为权值向量。

通过神经网络学习可得到网络相应权值与阈值，从而建立基于神经网络的水轮机模型，实际应用中，只需输入单位转速、导叶开度和桨叶角度，利用已建立的水轮机神经网络模型，就可计算水轮机输出流量和力矩。水轮机神经网络模型如图4所示。

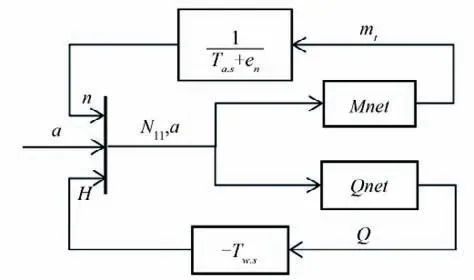
图4 神经网络模型方框图Fig.4 Neural network model block diagram

神经网络样本数据获取方法如下：

神经网络建模的依据为机组模型综合特性曲线，引入单位流量、单位转速和单位力矩如式：

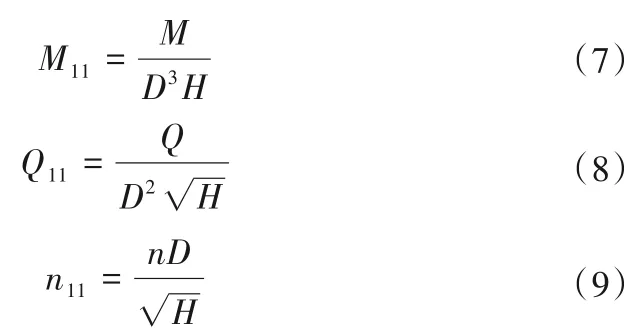
式中：M11为单位力矩；D为水轮机直径；H为水轮机水头；M为水轮机力矩；Q11为单位流量；Q为水轮机流量；n11为单位转速；n为水轮机转速。

单位转速n11、单位流量Q11、导叶开度α、桨叶角度β以及效率η是神经网络训练的输入数据。首先以n11和α为输入，单位流量Q11为输出得到第一组数据，训练出的神经网络即Qnet。其次以n11和Q11为输入，效率η为输出得到第二组数据。以一个拟合函数或者BP神经网络，使用第二组数据建立输入n11、Q11与输出η的关系式（10）。坐标变换后进行神经网络训练。利用关系式（10）与关系式（11），计算得出输入导叶开度α与单位转速n11对应输出单位力矩M11，即为神经网络Mnet。

式中：η为水轮机效率；α为导叶开度；γ=ρ g，γ为容重。

1.4 插值法水轮机模型

插值法水轮机模型与神经网络类似，也可描述水轮机非线性特性。神经网络模型是通过数据处理训练得到权值与阈值，在仿真时通过归一化后的单位转速n11与导叶开度α进行矩阵计算，再反归一化得出输出单位力矩与单位流量。插值法模型通过模型综合特性曲线数据计算得到插值表，在仿真时输入单位转速n11与导叶开度α，通过二元三次插值计算输出力矩与流量。神经网络模型需要前期样本数据多，但实时仿真输出数据误差相对小，插值法使用的插值表划分以及不同插值方法都会对最终结果产生影响。

插值法水轮机模型同样基于模型综合特性曲线建模，按照水头和开度划分工况，计算出对应工况点流量和力矩。仿真时输入单位转速与开度，采用二元三次插值法进行插值计算出全工况的流量与力矩。

二元三次插值公式为式（12）。

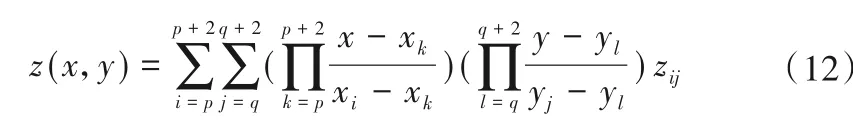
其中k≠i，l≠j，xp＜x＜xp+1，yq＜y＜yq+1。

其原理如图5所示。具体步骤为：

图5 二元三次插值示意图Fig.5 Binary cubic interpolation schematic diagram

设插值点为S，其坐标为S（xs，ys，zs），

（1）在插值点S周围找出9 个点A、B、C、D、E、F、G、H、I，且满足以下关系式：

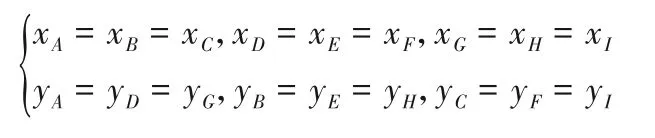
其中：xp＜xs＜xp+1，yq＜ys＜yq+1。

（2）分别对（A、D、G），（B、E、F），（C、F、I）进行一元三点拉格朗日插值，得到点（U、V、W）。

（3）对点（U、V、W）再进行一次一元三点拉格朗日插值，得点S，S点的值zs，s即为该插值点的函数值。

仿真时插值法模型与神经网络模型相似，都是输入单位转速与导叶开度，神经网络模型通过s 函数里编写的归一化及矩阵计算代码计算得出输出力矩与流量，插值法模型通过simulink 中2-D lookup table 模块实现插值，输出力矩与流量。模型方框图如图6所示。

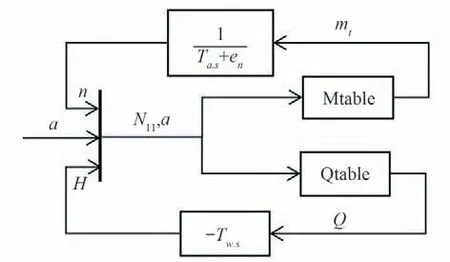
图6 插值法模型方框图Fig.6 Block diagram of interpolation model

2 仿真及对比实验

2.1 模型参数

某机组为混流式机组，该机组各参数如表1，神经网络权值与阈值如表2，神经网络输入输出关系曲面如图7 所示，插值表输入输出关系如图8所示。图中X轴为单位转速，Y轴为导叶开度，Z轴为输出流量或力矩。

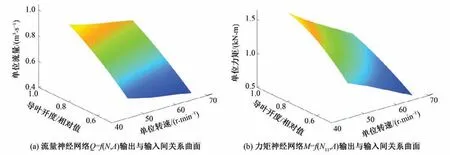
图7 流量与力矩神经网络Fig.7 Flow and torque neural network

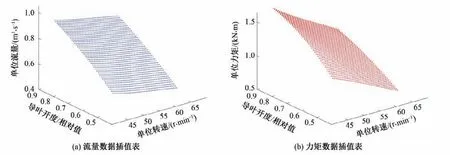
图8 流量与力矩插值表Fig.8 Flow and torque interpolation table

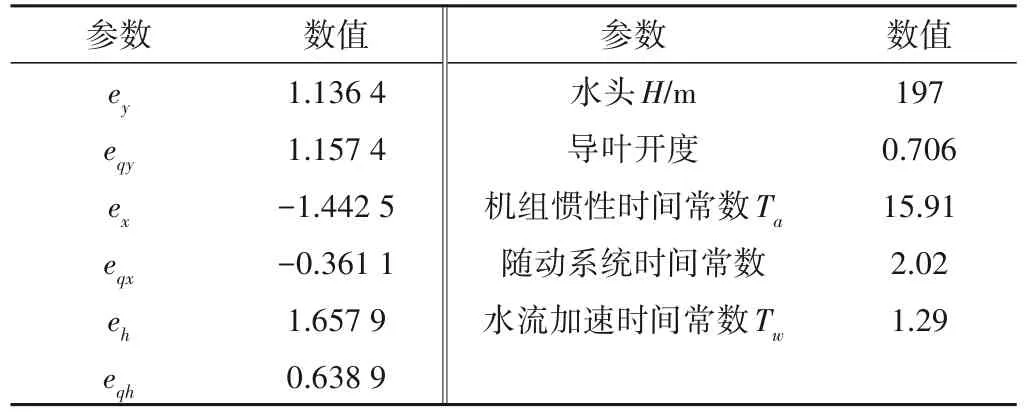
表1 额定工况参数Tab.1 Rated condition parameter

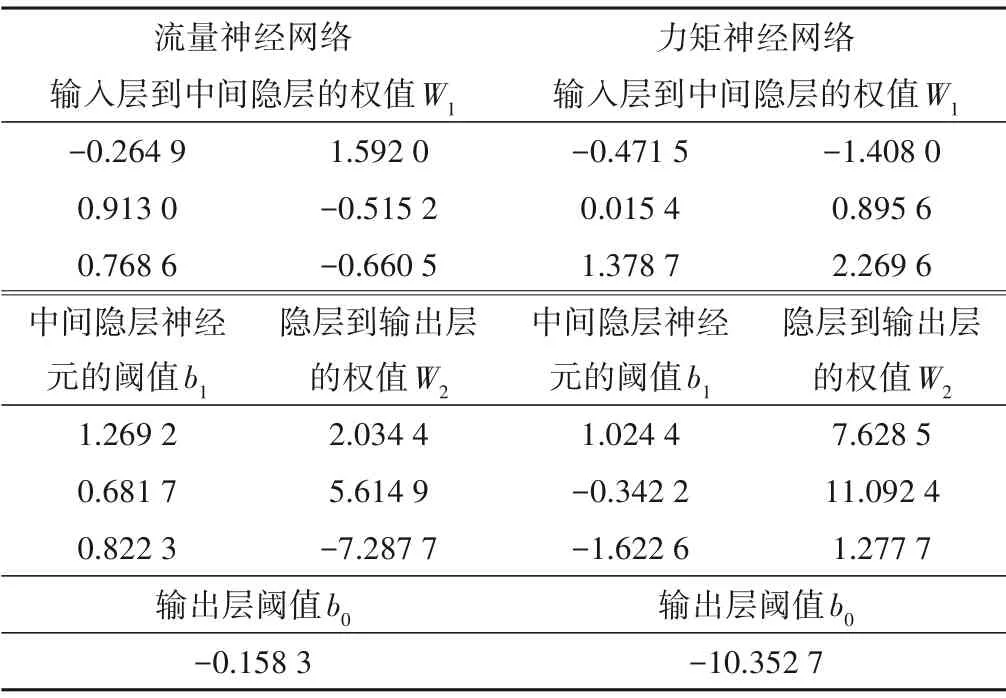
表2 神经网络权值与阈值Tab.2 Neural network weights and thresholds

调速器为并联型调速器，PID 参数为KP=0.20，KI=0.05，KD=0.05。分别以功率上调1%和10%为阶跃输入得到仿真力矩输出如图9（a）所示，流量输出如图9（b）所示，水头输出如图9（c）所示。

2.2 仿真结果分析

图9（a）为模型力矩输出，如图所示其中4 种模型稳态力矩相近，只有动态过程存在一定区别，其中分段线性化模型动态过程最快，理想水轮机模型动态过程最慢。图9（b）为模型流量输出，如图所示4种模型流量波动基本不同，其中理想水轮机模型的波动量最小，而神经网络模型和插值法模型的波动量最大，且稳态值相近。图9（c）为模型水头输出，如图9所示除插值法外水头波动稳态后基本相同，插值法在波动开始时水头产生较大瞬时变化然后趋于平缓。为更便于观察各参数变化，引入公式（13），对力矩、流量和水头变化进行对时间求导后，除以功率变化，处理得图10和11。

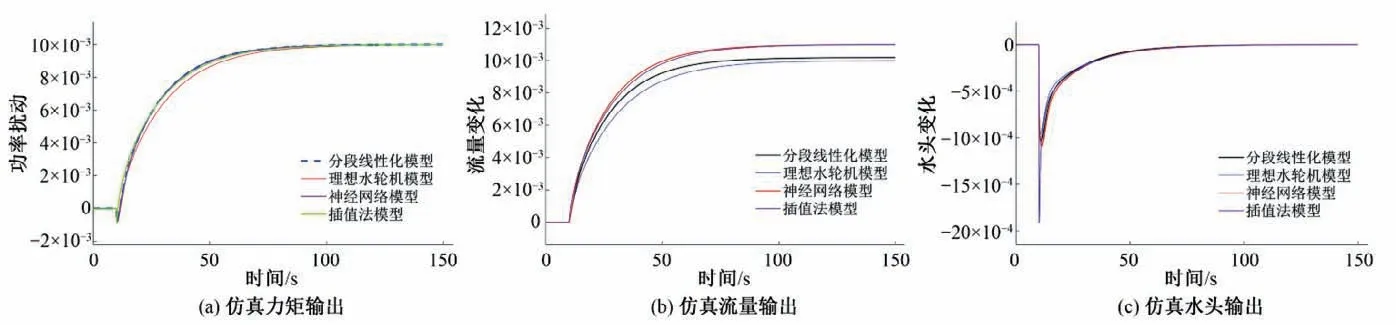
图9 仿真输出Fig.9 The simulation output

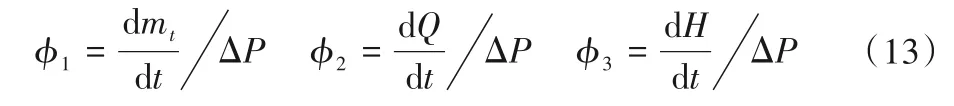
式中：t为时间；ΔP为机组功率变化；φ1为力矩导数对功率变化相对值；φ2为流量导数对功率变化相对值；φ3为水头导数对功率变化相对值。

由图10 可知在功率波动初期，插值法水轮机模型的φ1、φ2与φ3经过较大波动然后趋于平缓，其他3 个模型的φ1与φ2参数相近，只有φ3存在较大差别。由不同功率波动对比可知：功率波动对于φ波形变化影响较小。由图11可知：分段线性化模型仿真时间约为0.22 s，理想水轮机模型为0.21 s，插值法模型接近0.53 s，约为前两种方法二点五倍，神经网络模型仿真时间更长，为18 s左右。

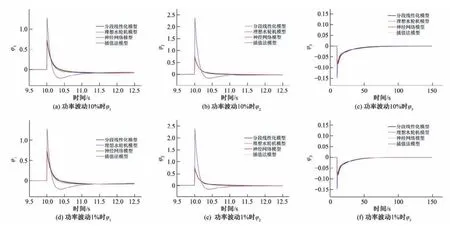
图10 不同功率波动时φ值变化Fig.10 The φ value changes with different powerfluctuations

图11 实际仿真时间Fig.11 Actual simulation time

3 结 语

本文建立了4种水轮机模型，并进行了仿真对比分析，结果表明：4种不同模型都能有效仿真力矩稳态特性，动态过程相差不大，而流量仿真时4 种模型输出相差较大。进行水头仿真时相比于其他3种方法，插值法模型水头波动会偏大，水头波动反映到蜗壳水压后会造成仿真蜗壳水压大于实际水压，进而使调节保证计算产生一定误差。仿真稳态力矩时四种模型精度相近，在动态过程存在一定差别，在波动瞬间若超出插值表边界处会产生水头瞬时较大波动，产生一定误差。

分段线性化模型在需要仿真时间较短和建模更简单时是较好的选择，当更多考虑动态过程精确度时，选择神经网络模型会更好。 □