圆柱形吸附装置内部的流场模拟

2021-11-29党明岩王复兴

沈阳理工大学学报 2021年5期

党明岩，王复兴

(沈阳理工大学环境与化学工程学院，沈阳110159)

吸附是化工分离的一种重要方法，吸附剂的制备工艺和吸附性能的改进是近年来的研究热点。诸多学者对新型吸附材料的制备及其化学改性进行了研究，王子然等[1]以KOH、K2CO3为活化剂制备了生物质活性炭材料，以碘吸附值和亚甲基蓝吸附值为评价标准，通过正交实验确定了最佳制备条件，实验结果显示其具有良好的吸附性能。刘玲等[2]通过磷酸三丁酯改性樟树叶，得到一种有机吸附剂，用于吸附植物中的铀，该吸附剂对铀的吸附速率快、吸附效率高，且可有效提取盐湖水中的铀，具有广阔应用前景与重要经济学价值。

壳聚糖类吸附剂由于其原料取材于天然产物，来源丰富，且具有多孔性结构，近年来受到较多关注。赵瑨云等[3]采用原位共沉淀法合成了羟基磷灰石/壳聚糖复合吸附剂，并用于吸附氟离子，探讨其吸附热力学和动力学。施周等[4]以膨润土、壳聚糖、Fe3O4为原料制备了磁性壳聚糖/膨润土复合吸附剂，通过静态吸附实验研究了其对Cu2+的吸附性能，确定了最佳吸附条件。

目前对吸附过程的研究内容多为静态吸附[5-6]，主要讨论静态吸附过程的等温吸附特性和吸附动力学[7-8]，且多数处于实验室研究阶段，对于更接近工业过程的动态吸附过程则研究较少。

动态吸附装置多为吸附剂填充形成的床层结构，吸附剂本身为多孔结构，流体在吸附装置内的流动既包括吸附剂颗粒间的流动，还有颗粒内的流动，故其内部流动状态较为复杂，对其内部流体流速以及压力的测定较难进行。流速和压力的变化会影响到流体与吸附剂的相互作用，进而影响吸附效果。近年来，随着计算流体力学的不断发展，对复杂流场进行数值模拟分析的方法也越来越成熟，为装置内部流场状况的研究提供了帮助。

本文采用数值模拟方法，以壳聚糖类吸附剂为例，以水作为流体介质，对有序堆积的吸附剂层内部流场和压力场进行研究。采用Solidworks软件建立物理模型，采用Fluent软件进行有限元分析，模拟计算结果可为动态吸附过程的深入研究提供理论基础。

1 物理模型

本文以吸附装置中的颗粒床层为研究对象进行分析。床层中的球状吸附剂有序堆积，形成圆柱形吸附装置，其物理模型如图1所示，其结构示意图如图2所示。壳聚糖颗粒孔隙率取为69%[9]，为避免产生无效网络，球状吸附剂之间的平均间隙设为0.5mm，其他尺寸详见图2。

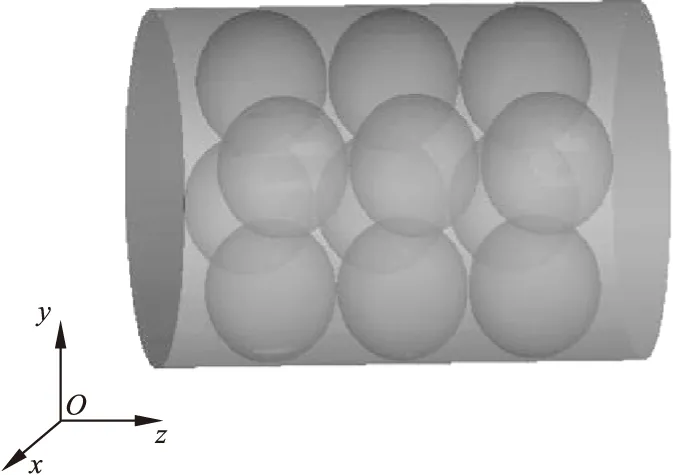
图1 吸附装置物理模型

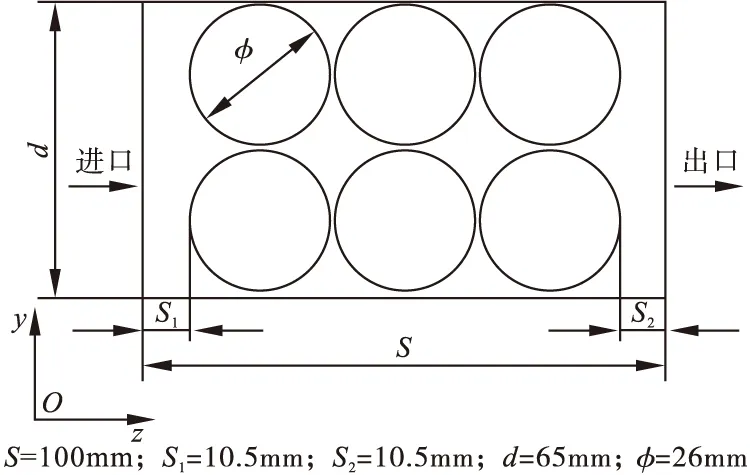
图2 计算区域结构示意图

2 数学模型

采用粘性定常不可压缩流体稳态流动模型进行计算流体力学(Computational Fluid Dynamics，CFD)分析，并作如下假设：

(1)不考虑重力因素；

(2)边界无滑移；

(3)不考虑温度变化。

数学模型由如下方程组成。

(1)Navier-Stokes方程

本文流体介质为牛顿型流体，其Navier-Stokes方程为[10]

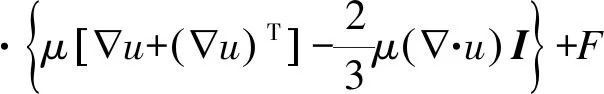
(1)

式中：p为流体压力；ρ为流体密度；t为时间；μ为流体动力粘度；u为流体速度；F为施加在流体上的外力；I为单位张量。

(2)连续性方程

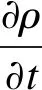
(2)

(3)湍流方程

按照初始条件计算雷诺数，结果显示流体进入吸附装置与吸附剂接触前为湍流流动，假设流体在吸附剂球体内流动为层流，选用k-ε湍流模型。k-ε模型具有较好的经济性、稳定性以及较高的计算精度，采用k-ε模型可更好地解决吸附过程的流体流动问题。k-ε模型属于第一类两方程模型，需要求解湍流动能k和耗散率ε的输运方程。

湍流动能k代表流体流动的紊乱程度，其输运方程为

(3)

式中：ui为沿i方向的流体流动速度；σk为k对应的普朗克数，取为1.0；μt为涡黏性系数；Gk为由平均速度梯度产生的湍流动能。μt计算式为

(4)

式中Cμ为模型常量，可由k-ε模型半经验公式推导，模拟计算中取为0.09。Gk计算式为

(5)

式中uj为沿j方向的流体流动速度。

湍流动能耗散率ε表示流动时的能量损失，其输运方程为

(6)

式中：σε为ε对应的普朗克数，取值1.3；C1ε、C2ε为经验常数，取C1ε=1.44，C2ε=1.92。

(4)多孔介质模型

球形吸附剂内部为复杂的多孔结构，按照多孔介质模型进行仿真模拟。相较于普通流体流动方程，多孔介质模型附加动量源项Si，其表达式为

(7)

式中：α为渗透因子；1/α为粘性阻力系数；C2为惯性阻力系数。α、C2可由欧根公式计算得出。

(8)

(9)

式中：θ为孔隙率；Dp为吸附剂颗粒当量直径。

3 网格划分与边界条件设置

3.1 网格划分

用ICEM-CFD对物理模型进行网格划分，划分网格优先选用六面体网格，吸附剂部分选用四面体网格进行划分，并对壁面网格进行加密处理。六面体网格具有质量好、收敛速度快等优点；四面体网格的适应能力强，能够更好地填充复杂的几何形状。网格划分如图3所示。

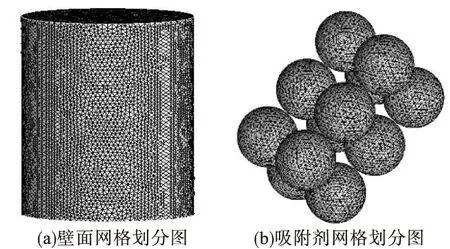
图3 吸附装置计算网格

划分网格数量共有731233个单元，节点总数为135779，最小网格无负体积出现，网格总体质量良好。

3.2 网格无关性验证

数值计算所需要的网格与所采用的算法密切相关。理论上来说，网格布置越密集，所得计算结果越精确，但是过密的网格也会导致计算周期增大。为验证所划分网格的可靠性，计算中另外将网格划分为783000个进行模拟，所得结果与低网格下模拟结果相同，说明数值计算在低网格下已经收敛，模拟结果可靠。

3.3 边界条件设置

进口条件：速度为0.05 m/s，湍流强度为5%。

出口条件：出口表压为0，湍流强度为5%。

壁面条件：将壁面条件设置为WALL，忽略壁厚的影响，圆管壁面为固体壁面。流体和固体的接触面均设置为耦合面。

模型计算采用SIMPLE方案，求解精度设为二阶迎风格式，速度项、湍流动能项等采用Fluent软件自带方程及参数进行求解计算。设置亚松驰因子为0.001，迭代200次。

4 模拟计算结果分析

分别选取穿过吸附剂球体中心的yoz平面和xoy平面进行分析，模拟计算得到吸附装置内部流体的压力和速度分布规律。

4.1 yoz平面压力分布

图4所示为yoz平面上径向位置x=13.25mm处的压力云图。

图4 yoz平面压力云图

由图4可见，流体进入吸附装置后，随着其向出口方向移动，压力逐渐降低，即压降逐渐增大；流体流经吸附床层时，流通面积减小，速度增大，压降随之增加；吸附剂球体接触间隙处的压力与其他位置压力相比明显较大；流体流动过程中，吸附剂外侧流体与吸附剂球体内部流出液体交汇，形成压力涡。

4.2 xoy平面压力分布

图5所示为圆柱形吸附装置内xoy平面上的径向压力云图。其中图5a、图5b、图5c分别对应轴向位置z1=23.5mm、z2=50mm、z3=76.5mm。

由图5可见，当液体流入吸附剂球体时，压力明显降低，在球体内部压力变化较小，由于孔隙的存在，吸附剂球体内压力云图区别于外侧压力分布。对比图5a、图5b和图5c可以看出，随着流体向出口方向移动，吸附剂球体内部与球体壁面处的压差逐渐减小。因吸附装置壁面附近的空隙率大于吸附装置内部，液体在近壁处的阻力较小，压力较大，表现为“壁效应”。

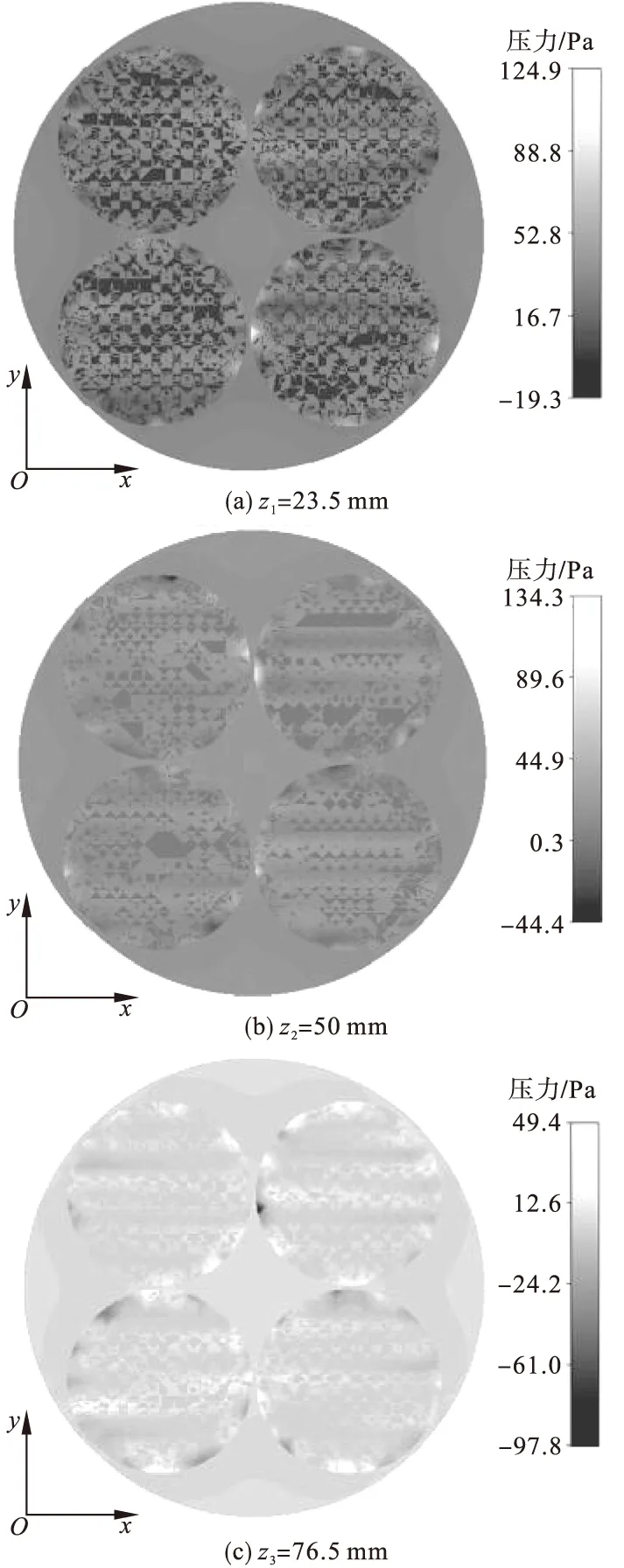
图5 xoy平面不同轴向位置压力云图

4.3 yoz平面速度(矢量)分布

图6所示为yoz平面上径向位置x=13.25mm处的速度云图。

由图6可见，流体在多孔介质内流速很低，因不考虑边界滑移，流体在两侧壁面处速度大致成对称分布，且壁面附近流体流速明显大于吸附装置内其他位置处流速。该截面区域内可见几处漩涡，分别位于吸附剂球体衔接处与出口处位置。漩涡会引起速度分布不均，也会导致能量损失增大。从速度云图来看，流体从进入吸附剂内部到流出，其速度变化不明显，故可认为流体在吸附剂球体内部流动为层流流动，符合假设条件。

图6 yoz平面速度分布云图

yoz平面上x=13.25mm处速度矢量图及局部放大图如图7所示。

图7 yoz平面速度矢量云图及局部放大图

由图7可以看出，在吸附装置内流体大体呈轴向流动，但在出口位置与吸附剂球体衔接处可见回流和漩涡，产生切向流和径向流，切向速度分量产生的离心力引起明显的离心对流作用，导致吸附剂内流出的流体与壁面附近的流体混合，影响吸附效果。

4.4 xoy平面速度分布

图8所示为xoy平面上圆柱形吸附装置的径向速度云图。其中图8a、图8b、图8c分别对应轴向位置z1=23.5mm、z2=50mm、z3=76.5mm。

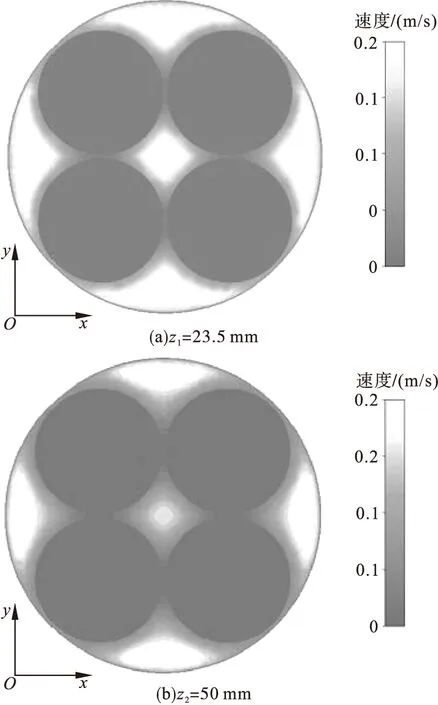
图8 xoy平面不同轴向位置速度云图

由图8a可见，当液体刚刚流入吸附装置时，速度偏低，吸附剂球体内液体流出不明显，少量流出液体也会很快被后续进入液体带入到下一阶段；由图8b和图8c可见，随着液体沿轴向向出口流动，近壁面处流速明显增大，液体从吸附剂内流出愈加明显，更多液体达到吸附剂内部，充分利用吸附活性位。此外，越近出口，吸附剂内流出液体与吸附剂外流体交汇混合越剧烈。