FFT-CNN-GRU模拟电路故障诊断方法研究
2021-11-29刘伊鹏徐万洲
刘伊鹏,徐万洲,杨 青
(沈阳理工大学 自动化与电气工程学院,沈阳 110159)
数字电路和模拟电路是电路系统的重要组成部分。与数字电路相比,模拟电路要解决内部干扰问题,且结构比较复杂,其研究进展远落后于数字电路。随着现代工业的发展,数字电路和模拟电路结合使用已是大势所趋,电路的复杂程度也大幅度提高,导致电路发生故障的几率也有所增加。电路系统在运行期间发生意外电路故障,会严重损害企业的经济利益和人身安全。模拟电路发生故障的概率远大于数字电路,资料显示[1],数字电路的应用程度达到80%左右,但大约80%的故障由模拟电路引起,模拟电路对整个电路系统有重要影响,对其故障的研究日益受到关注。
深度学习对数据有强大的学习能力,相比于浅层学习的深度架构,其克服了在训练上出现的难度问题。近年来,学者们开始将深度学习方法运用于模拟电路故障诊断方面的研究。文献[2-3]将卷积神经网络应用在模拟电路故障诊断中,将收集的一维数据直接作为一维卷积输入进行特征提取,保证原始数据的基本特征,防止数据丢失,再使用分类器进行故障分类。文献[4]使用卷积神经网络(Convolutional Neural Network,CNN)提取特征,然后采用支持向量机(Support Vector Machine,SVM)进行故障分类。
由于模拟电路存在元件容差等问题,导致原始故障数据之间区分不明显,故需对数据进行预处理。目前常用的预处理方法是小波变换[5-6],其难点是小波基的选取,小波基选择不当会影响故障诊断性能。快速傅里叶变换则可将原始信号从时域转换到频域,使特征变得更加明显,且快速傅里叶方法不需要小波基函数的选取。
本文采用快速傅里叶变换对一维数据进行预处理,该处理过程无需参数的定义;再将得到的一维数据作为卷积神经网络和门控循环单元的输入,对故障类型进行识别,并验证该方法的诊断效果。
1 FFT-CNN-GRU方法
1.1 快速傅里叶变换(FFT)
快速傅里叶变换(Fast Fourier Transform,FFT)将时域信号无法体现的信息在频域信号中体现出来,其本质为离散傅里叶的一种优化算法,可简化计算量,加快计算速度。其原理为:以大小为fs的频率对原始故障信号进行采样,采样点数为N,经过FFT之后,将得到N个复数点,每个复数对应一个频率值,每个点的相位代表频率分量的相位,每个点的幅值代表频率分量的幅值。
1.2 CNN模型
CNN是神经网络算法的一种[7],其在图像处理方面效果非常显著,得到广泛应用,也被用于处理一维数据。卷积层、池化层和全连接层为CNN的主要模块。卷积层主要是将目标对象输入层的信息进行局部区域的特征提取,多个卷积单元构成卷积层,卷积层对数据进行提取;池化层对数据进行特征降维,去除冗余信息,降低过拟合风险;全连接层在卷积神经网络中起到分类作用,其每一层均由许多神经元组成,每个神经元并不独立存在,其与下一层的神经元进行一一相连,可将得到的特征图展开平铺进行运算,对特征图谱达到更好的分类效果。CNN结构如图1所示。
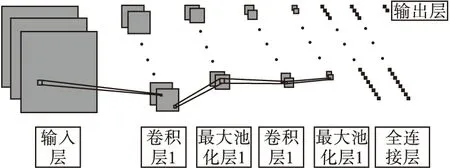
图1 CNN结构图
1.3 GRU模型
门控循环单元(Gate Recurrent Unit,GRU)是长短期记忆网络(Long Short-Term Memory,LSTM)的升级,但在结构上大大简化。LSTM通过门控来记忆重要信息,同时选择忘记非重要信息。GRU减少了参数,加快了收敛速度,可更好地解决梯度消失问题[8-9]。GRU的更新门和重置门控制最终留下的有用信息,且不会随时间变化而清除以前的信息,其更新门等同于LSTM的遗忘门和输入门。GRU结构如图2所示。
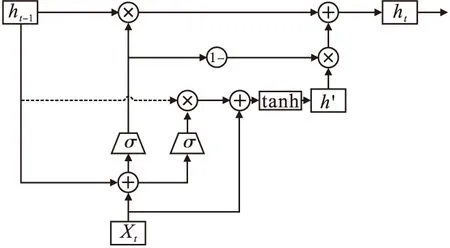
图2 GRU结构图
GRU公式如下。
zt=σ(wz·[ht-1,xt])
(1)
式中:zt为更新门;σ为sigmod函数;wz为更新门的权重参数;xt为当前时刻的输入;ht-1为上一时刻的输出。
rt=σ(wr·[ht-1,xt])
(2)
式中:rt为复位门;wr为复位门的权重参数。
h′t=tanh(wh·[rt*ht-1,xt])
(3)
式中:h′t为当前时刻的待定输出;wh为待定输出的权重参数。
ht=(1-zt)*ht-1+zt*h′t
(4)
式中ht为当前时刻的输出。
1.4 FFT-CNN-GRU算法
本文采用的CNN-GRU模型属于融合模型,包括FFT、CNN和GRU三个部分。其结构如图3所示。
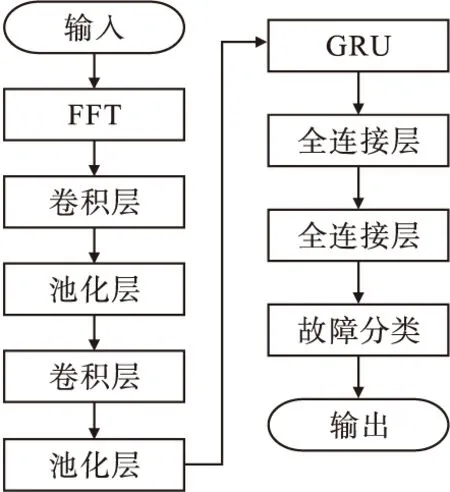
图3 FFT-CNN-GRU结构图
由图3可见,应用FFT-CNN-GRU算法时,首先采用FFT对数据预处理,然后采用卷积神经网络对数据进行特征提取,池化层对数据进行二次特征提取,相当于降采样的过程,最后将降维后的数据作为GRU的输入训练模型,由softmax分类器完成最后的分类。利用CNN网络局部特征能力的优点及GRU网络对数据的挖掘能力,搭建CNN-GRU的故障诊断模型,该模型同时具备时间、空间的特征[10]。
2 实验部分
为验证本文提出的故障诊断方法,实验中将状态变量滤波器电路[11]作为待测电路,如图4所示。仿真实验以Multisim14作为实验平台,数据预处理采用Matlab2018a完成,故障模型的搭建由python3.6完成。
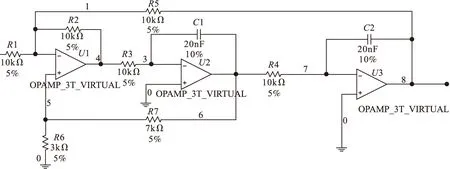
图4 状态变量滤波器
设置电阻和电容的故障正常值分别为:R1=R2=R3=R4=R5=10kΩ;R6=3kΩ;R7=7kΩ;C1=C2=20nF。将该电路的R1、R2、R5、C1、C2作为单故障检测元器件,考虑元件本身的容差变化,设置电阻容差为5%,电容容差为10%,若浮动超过容差的50%时为元件故障。具体故障类别与故障值如表1所示。
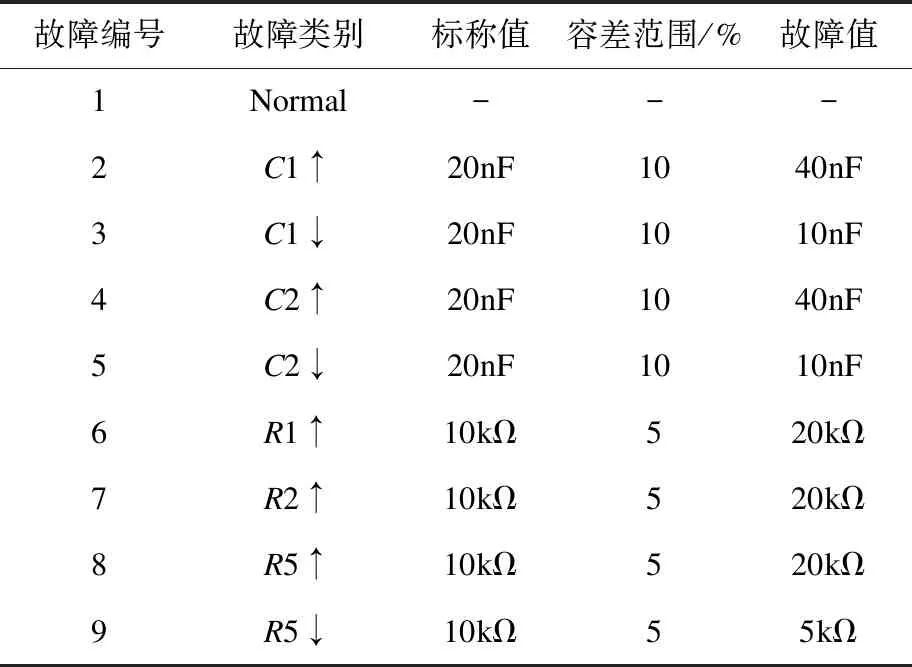
表1 故障类别与故障值
利用Multisim软件建立模拟电路,被测电路的激励信号设为500Hz-1V交流激励。设置某一元件为故障状态,其余元件为正常状态,采用蒙特卡洛分析法在输出节点采集电路的电压信号,获取各元件故障时电路输出的电压信号数据。
采用蒙特卡洛分析时,每种故障进行100次分析,得到900组样本数据,随机抽取70%为训练集、20%为测试集、10%为验证集。将该方法与其他方法进行对比,结果如表2所示。

表2 故障诊断结果对比表
由表2可见,本文采用的FFT-CNN-GRU方法在故障诊断中取得较高的准确率,明显优于其他方法,说明其在模拟电路故障诊断中可行。
将FFT-CNN-GRU模拟电路故障诊断方法应用到状态变量滤波器电路,为验证该模型的有效性,设置模型的迭代次数为500次,通过训练得到准确率曲线和损失变化曲线如图5和图6所示。
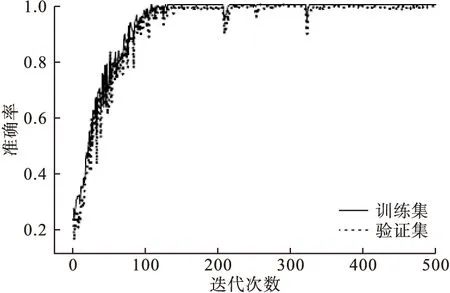
图5 迭代收敛曲线图
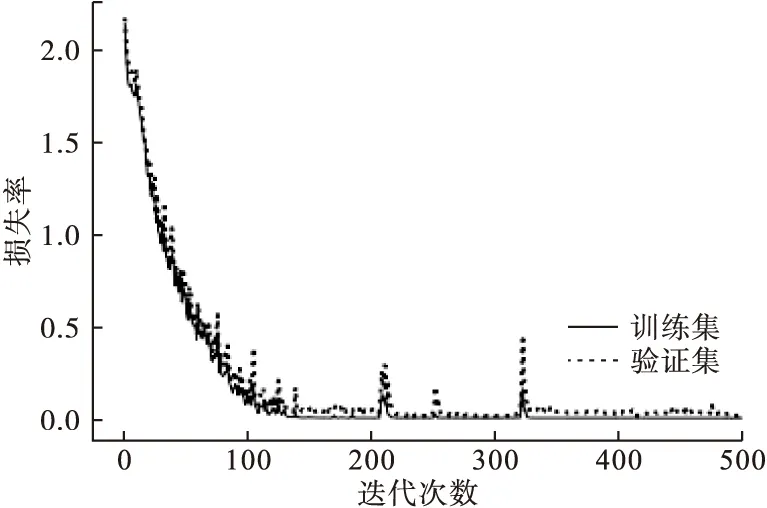
图6 损失函数曲线
由图5和图6可见,当迭代次数达到110左右时,准确率可达到97%左右;迭代次数达到320左右时,损失函数曲线达到稳定状态,说明本文采用的模型训练速度较快,故障诊断精度高,可有效应用于模拟电路的故障诊断。
3 结论
采用FFT-CNN-GRU对模拟电路进行故障诊断,将故障诊断的预处理、特征提取和分类相结合,对状态变量滤波器电路得到的仿真数据集进行验证,结果表明FFT-CNN-GRU方法优于传统机器学的方法,在模拟电路故障诊断中可达到良好的效果。后续研究中可引入其他算法来优化网络模型,进一步地提高故障诊断准确率。
