基于序列优化的DS/FH通信体制通信性能分析

王思奇，蒋 强，刘 涛

(1.沈阳理工大学 a.信息科学与工程学院，b.自动化与电气工程学院，沈阳 110159；2.陆军装备部装备项目管理中心，北京 100072)

直扩/跳频(Direct sequence spread spectrum/Frequency Hopping spread spectrum，DS/FH)结合扩频系统利用直扩系统中信号功率谱密度低于噪声功率谱密度的特性，发挥隐蔽通信的作用，又通过跳频获得较大的频谱宽度，兼具较强的抗干扰能力[1]。DS/FH结合扩频系统不仅可以综合两种扩频通信技术的优点，而且可以改善单一直接扩频系统较差的远近特性及单一跳频系统在慢跳时隐蔽性差等不足之处。

跳频和扩频通信系统对性能优良、码数大、序列数长的伪随机序列的需求越来越高，常用的m序列和gold序列难以满足其要求。混沌序列具有伪随机性和初值高敏感度的特性[2]，理论上可产生无限种合格的伪随机序列，大大增加了编码用户的数量。与传统的随机序列相比，混沌系统能够占用最小的资源而产生最大长度的序列。大多数用于产生混沌序列的混沌映射具有参数范围局限性及均匀分布性，以常用的Logistic映射为例，当参数被选择在规定范围之外时，将导致周期信号分布均匀，安全性有所降低[3]，即使在参数范围内，也会出现周期窗口现象，影响其混沌性能。

本文从DS/FH结合通信体制出发，应用变换函数对Logistic映射进行改进，提高系统的参数范围，变换后Logistic映射的混沌序列得到优化，具有良好的相关特性并为DS/FH结合扩频体制提供良好的抗干扰性。

1 改进的混沌DS/FH结合扩频体制

一般DS/FH结合扩频通信体制中，初始基带信号首先进行直接序列扩频操作，然后用伪随机序列发生器控制跳频振荡器，使载波发生跳变，变化的载波再对直接扩频序列进行一次调制。调制模块最终产生中频频率与跳频相加的信号，调制后的信号通过射频模块传输。接收机按照先解跳再解扩的流程处理信号，最终恢复原始基带信号[4]。

普通跳扩结合系统分别产生直接扩频部分和跳频部分。本文将系统参数设入变参系统，混沌序列发生器控制直扩序列和跳频序列实时产生，跳扩信号中直扩部分和跳频部分可作为一个二维系统。改进型混沌DS/FH结合扩频通信系统总体框图如图1所示。

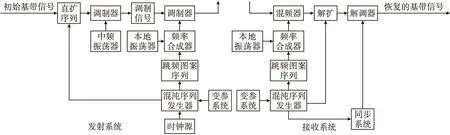
图1 改进型混沌DS/FH结合扩频通信系统总体框图

由图1可见，直扩序列和跳频序列由同一个混沌序列发生器产生，在仿真时可降低复杂度。变参系统由跳频初始值、跳频频率集、每一跳的持续时间、直扩序列码元宽度等组成。收发双方具有同样的变参系统即可完成正确接收。因混沌序列具有初值敏感性，且变参系统的参数易于控制和改变，一个参数变化即导致完全不同的结果，极大地增加了非接收方破译传输信息的难度。

2 混沌序列的优化及性能分析

Logistic映射由Logistic函数演化而来，公式为

x(n+1)=μx(n)(1-x(n))

(1)

式中：x为自变量；n为自变量的迭代次数；μ为Logistic映射的初值参数。

Logistic映射中混沌序列的产生与μ值直接相关。在典型Logistic映射中μ的取值范围为[3.569946，4]，其选择范围有限，当μ值不在范围内时不会产生混沌现象。为优化μ值的可选范围，采用余弦变换为

μ=0.205sin(μ′)+3.795

(2)

式中μ′为对μ进行优化处理的处置参数。将式(2)代入式(1)，得到

x(n+1)=[0.205sin(μ′)+3.795]x(n)[1-x(n)]

(3)

此时μ′取值为(-∞，+∞)，任何μ′值均可使优化后的Logistic映射进入混沌状态。

2.1 混沌特性分析

采用最大Lyapunov指数来验证优化后映射的混沌特性。Lyapunov指数反映相邻两个数据初始状态多次迭代后运动收敛和分离的整体情况，其公式为

(4)

式中：λ为Lyapunov指数；F(x)为一维系统。

优化前Logistic映射的最大Lyapunov指数图及分岔图如图2所示。

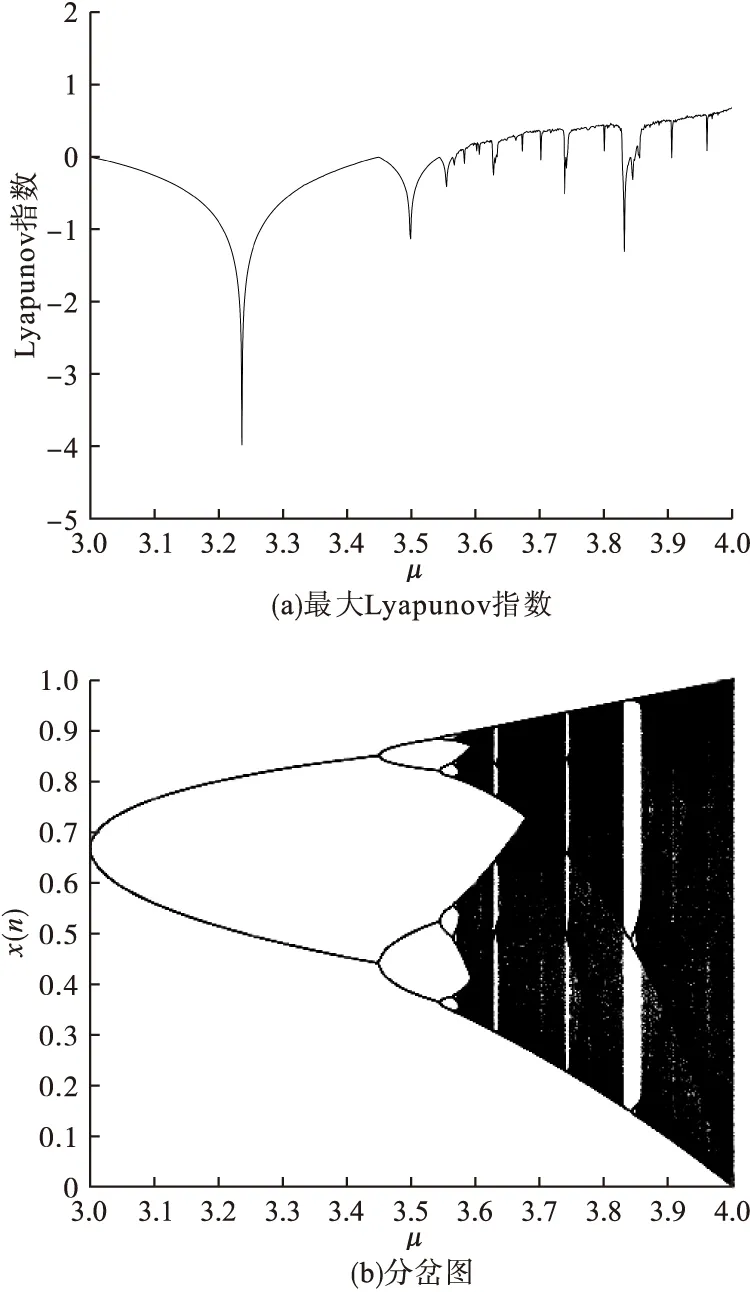
图2 优化前Logistic映射的最大Lyapunov指数图及分岔图

由图2a可以看出，当μ值小于3.56时，最大Lyapunov指数为负值，即不产生混沌。分岔图(图2b)显示出同样的结果，μ值被限制在固定点。

优化后Logistic映射的最大Lyapunov指数图及分岔图如图3所示。

由图3a可以看出，当μ值在9.87～10.08和12.31～12.56两段区间时，最大Lyapunov指数为负值，即不产生混沌。μ值在其他区域时，最大Lyapunov为正值，能产生混沌。Lyapunov指数增大，说明混沌系统的初值敏感性提高，极大地改善混沌信号的随机性。优化后的Logistic映射分岔图混沌序列的参数取值范围有了极大程度的扩展(图3b)，证实优化后的Logistic映射与普通Logistic映射相比，参数限制范围降低，更容易出现倍周期现象，进入混沌状态[5]。

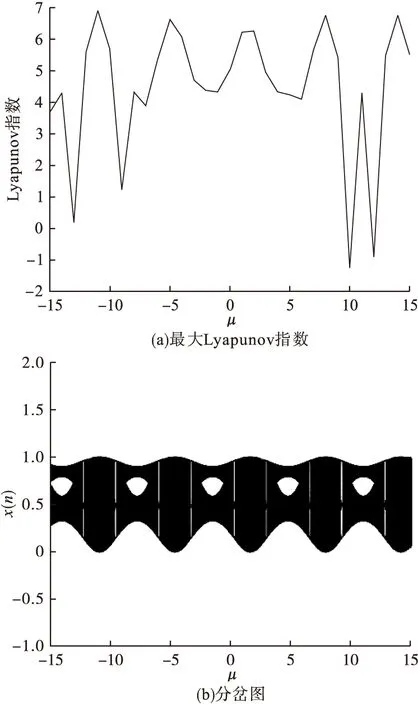
图3 优化后Logistic映射的最大Lyapunov指数图及分岔图

2.2 相关特性分析

为满足扩频通信系统的要求，混沌序列要具有尖锐的自相关函数，而互相关函数近乎于0，才能保证扩频系统具有抗多径干扰及多址干扰的能力[6]。将优化后的Logistic映射作为伪随机序列，分析其对于混沌序列发生器产生的直扩序列和跳频序列的相关特性。

假设序列{PN1(t)}、{PN2(t)}为由不同初值得到的两个直扩序列，则{PN1(t)}、{PN2(t)}的归一化互相关函数为

(5)

其中

(6)

式中：N为直扩序列长度；k为步长。

当N→∞时，混沌跳扩信号发生器产生的直扩序列具有渐进理想的部分互相关特性，即

(7)

归一化自相关函数为

R(k)=Raa(k)

(8)

当N→∞时，混沌跳扩信号发生器产生的直扩序列具有渐进理想的部分自相关特性。即

(9)

在跳频通信系统中，两个以上用户在同一时间内共用同一频率时，会产生用户之间的相互干扰[7]。一般采用周期汉明相关函数衡量跳频序列性能，公式为

(10)

式中：x、y为两个跳频序列；M为跳频序列长度；τ为时延。h取值为

(11)

汉明自相关函数的旁瓣为

Hxx(τ)， 1≤τ≤M-1

(12)

当M≥q(q为跳频频率集)时，混沌跳频序列的汉明相关函数满足均值为M/q、方差为(Mi-M/q)2的高斯分布。

直扩序列部分相关特性图如图4所示。

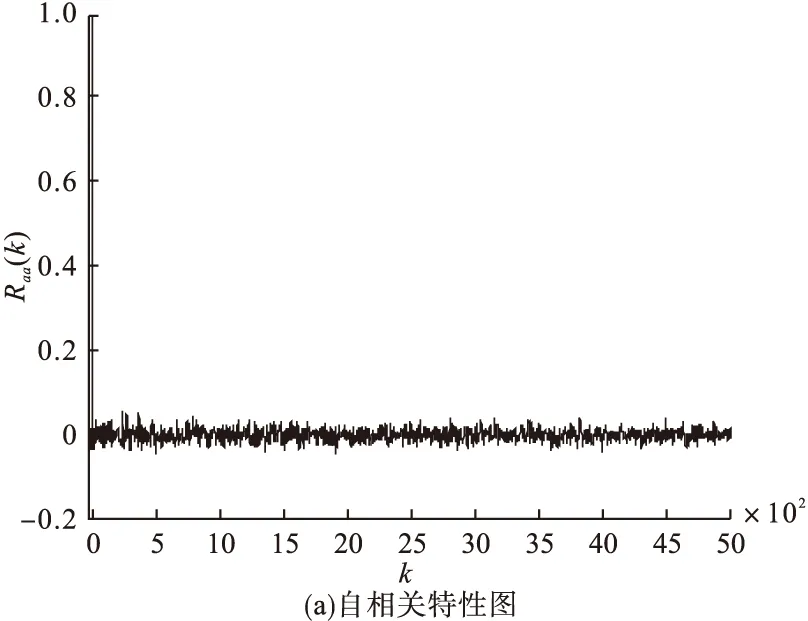
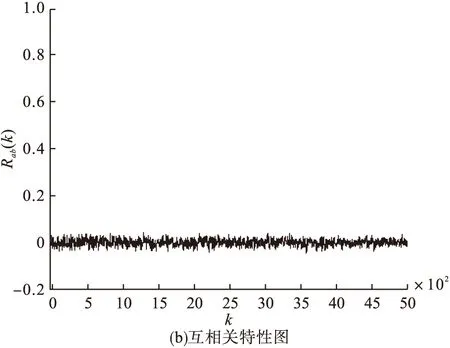
图4 直扩序列部分相关特性图

当步长变化时，自相关系数变化越小，说明对应的序列随机性越好。互相关函数取值越接近0，说明两个序列越互不相关，差异程度越大。由图4可以看出，由优化后的Logistic映射作为伪随机序列产生的直扩序列具有理想的相关特性。

跳频序列汉明相关特性图如图5所示。

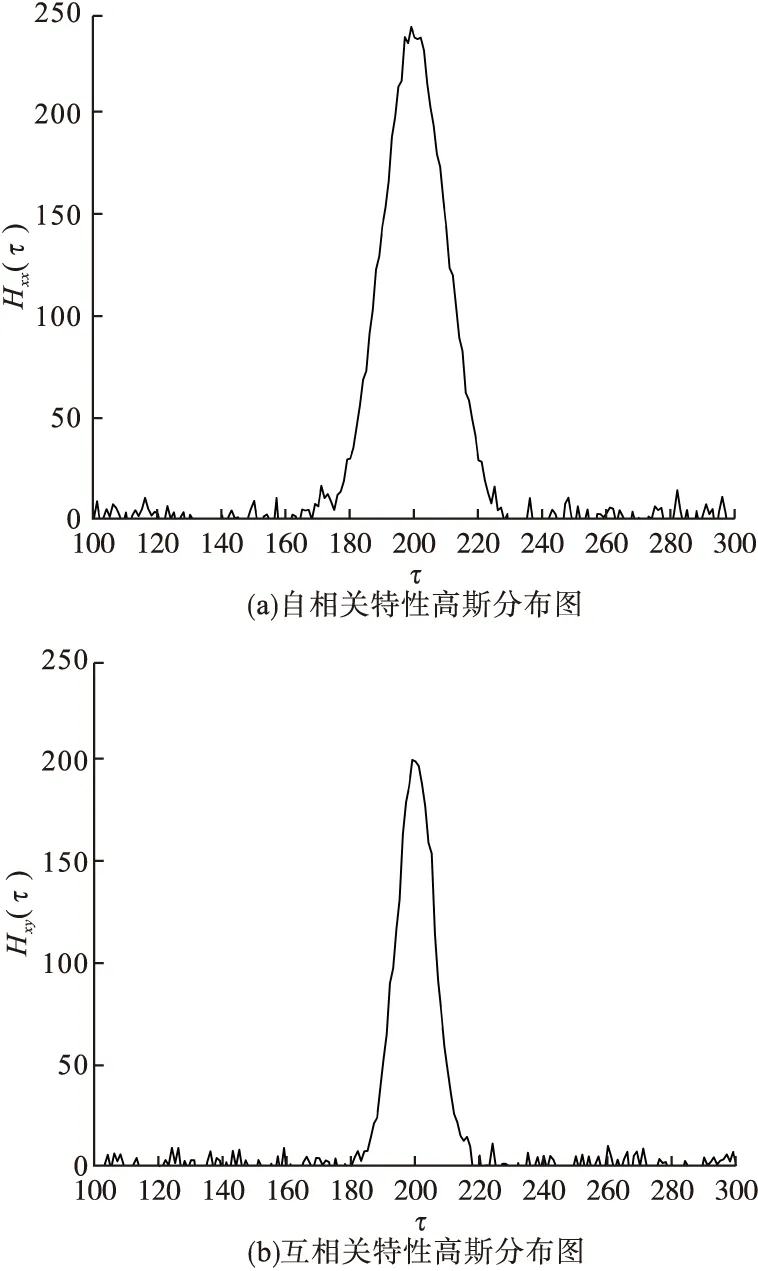
图5 跳频序列汉明相关特性图

由图5可知，跳频序列的分布曲线范围符合理想相关值分布曲线范围，表明跳频序列具有理想的汉明相关特性，说明优化后的Logistic映射作为伪随机序列可对抗干扰。

3 抗干扰特性分析

直扩系统的数据处理增益主要受扩频编码速率及信元码速率的约束，而跳频系统在跳频速率不高时易被跟踪和干扰[8]。DS/FH结合系统对单一直扩系统和跳频系统的局限性进行了改善。

扩频系统的抗干扰能力由其干扰容限决定，干扰容限则根据系统扩频增益来确定[9]。由于频谱有限，扩频增益不可能无限度增加，当干扰信号的功率大大超过扩频通信的干扰容限，扩频增益远远不够。若无法保证传输的有用信号进行可靠译码，则通信性能急剧减弱[10]。

本文以梳状干扰为例进行仿真分析。根据DS/FH的基本原理和抗干扰要求，设置跳速为500跳/s、符号速率为20kbp、带宽为25kHz、跳频频点取64个、最大频偏为5kHz，两跳之间留有100kHz的空隙。梳状谱干扰参数设置为覆盖带宽为5MHz、子信道带宽为50kHz、每一个信道间隔为25kHz，干信比从-10dB升至+15dB，步长取为1bB。仿真得到优化前后两种序列抗梳状干扰效果如图6所示，图中以误码率和干信比的关系表达抗干扰效果。

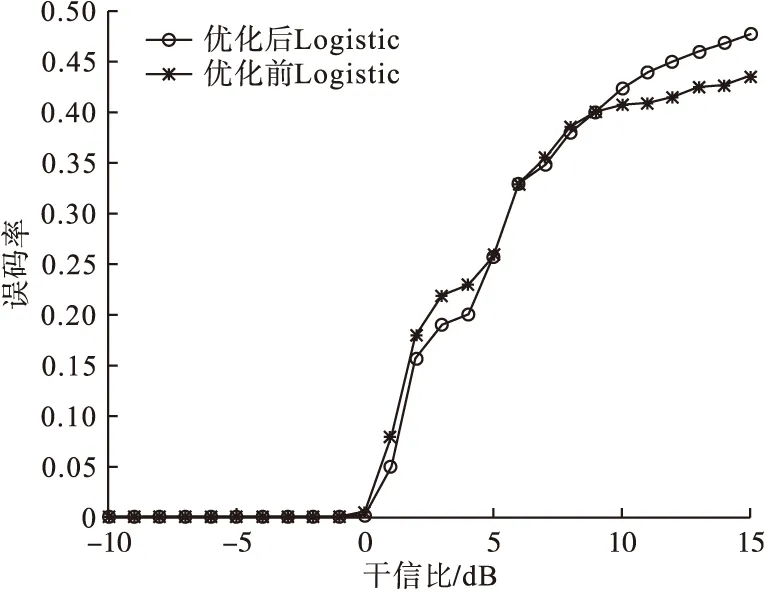
图6 优化前后两种序列抗梳状干扰效果

由图6可以看出，在其他干扰参数相同的条件下，采用两种伪随机序列的干扰样式的误码率随干信比变化趋势近乎一致。当干信比小于0dB时，两者对应的误码率接近于0；当干信比大于10dB 时，优化后的Logistic映射作为伪随序列的混沌跳扩频体制的抗梳状干扰能力明显好于优化前。

4 结论

DS/FH体制将直扩体制和跳频扩频体制进行结合，不但利用直接扩频技术使信号的功率谱密度远低于噪声的功率谱密度，达到抗截获的主要目的，还利用跳频扩频技术获得超大信号频谱宽度，使得该系统同时具有较强的抗干扰能力。通过函数变换优化的Logistic映射前后对比分析表明，优化后的混沌映射不受参数范围限制，更容易进入混沌状态。对混沌序列发生器产生的直接扩频序列及跳频序列的相关特性分析表明，优化后的Logistic映射产生的混沌直扩序列及跳频序列具有良好的相关特性。针对混沌跳扩频体制的抗梳状干扰性能进行仿真分析，结果表明采用优化后的Logistic映射作为伪随序列的混沌跳扩频体制抗梳状干扰能力更强。