基于贝叶斯方法的冲击试样测量不确定度评估
2021-11-28李海蓉靳俊杰刘方义
李海蓉,彭 煜,胡 翔,靳俊杰,包 福,刘方义,姜 明
(1.湖北省计量测试技术研究院,湖北 武汉 430223;2.武汉纺织大学 材料科学与工程学院,湖北 武汉 430200;3.武汉纺织大学 计算机与人工智能学院,湖北 武汉 430200)
冲击试验是确定产品及设备在经受冲击负荷作用时产品的安全性、可靠性和有效性的一种试验方法[1-2]。为了保证冲击试验机示值的准确性,必须对其进行计量检定/校准。而用标准冲击样品对冲击试验机进行计量,能够评定冲击试验机的综合性能,或对设备问题进行追溯,是一种准确、简单、高效的计量手段。
不确定度评估的目的是探知测量结果的准确和可靠程度[3-10]。GUM(The guide to the expression of uncertainty in measurement)[11]提供了测量不确定度的指导方法。它通过测量方程建立起误差元变量与被测量之间的关系,从而确保误差之间的可传递性。GUM S1[12]基于数值计算方法通过Monte-Carlo方法实现概率密度函数的抽样。它也可看作是一种特殊先验条件下基于贝叶斯方法(Bayesian method)的不确定度评估[13-14]。基于贝叶斯方法评定不确定度的研究大多采用A类评定,但通常未考虑完整测量方程[15-18]。
本文在考虑多源测量不确定性基础上,通过对ABS共聚物冲击试样进行冲击测试,建立适当的测量方程,分别通过GUM标准评估方法与非线性系统的贝叶斯方法对评定数据源进行分析,并对二者结果进行对比与评价。进一步,我们提出简单重复性取样,优化贝叶斯方法的先验选取方案不足,以此,我们得到更置信的贝叶斯评估方案。
1 评估方法
1.1 数学模型
依据GBT1043.1-2008标准制备A型冲击试样,试样原料为丙烯腈-丁二烯-苯乙烯共聚物(ABS,TAIRILAC 15A0)。样品冲击强度为
(1)
式(1)中:Ec为样条冲击强度,kJ/m2;c为冲击能,J;h为样条在缺口处的厚度,mm;b为样条剩余宽度,mm。
由式(1)可知,冲击样条的测量不确定度包括冲击能c的测量不确定度、样条在缺口处的厚度h的测量不确定度以及样条剩余宽度b的测量不确定度三个部分,且互不相关,因此样条冲击强度的标准不确定度的计算公式如下:
(2)
1.2 误差源分析
1) 在冲击试样尺寸测量过程中引入的不确定度
包括测量缺口处的厚度,以及宽度所引入的不确定度分量。此类不确定度评定需经过重复性的实验进行统计计算,进行A类不确定度评定。
2) 由于冲击能修正而引入的不确定度
该分量与实验仪器的精度和冲击实验过程中摆锤能量损失有关,无须开展重复性实验,进行B类不确定度评估。
3) 由于实验数据修约而引入的不确定度
进行B类不确定度评估。
4) 与冲击强度测量重复性相关的不确定度
进行A类不确定度评估。
1.3 GUM方法评估
根据JJF 1059.1-2012《测量不确定度评定与表示》进行GUM法不确定度评估。
1.4 贝叶斯方法评估
将参数μ看作随机变量,且测试前具有关于参数μ的所有信息的先验分布,通过测试得到数据X=(x1,x2,x3,…),结合X和先验分布得到参数μ的后验分布。后验分布包含了μ的所有信息,因此对μ所作的任何计算都基于后验分布。
贝叶斯理论可简单表示为
h(μ|x)∝p(μ)L(μ|x)。
(3)
式中:h(μ|x)为后验密度函数,p(μ)为先验密度函数,L(μ|x)为样本密度函数,即似然函数。
当测量样本(x1,x2,x3,…)相互独立时,上一次的后验分布可以作为下次计算的先验分布。根据历史测量数据得到先验均值μ0和均值的先验标准差τ,并假设测量数据服从正态分布,因此可认为p(μ)~N(μ0,τ2),得到均值μ的先验密度函数为
(4)
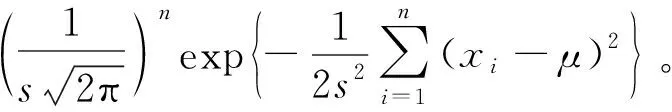
(5)
将式(4)和(5)代入式(3)得到后验分布为
(6)
其中,
(7)
(8)
2 测试结果与分析
利用XJJ-50型简支梁冲击试验机对样条进行冲击测试,得到数据如表1所示。
2.1 测试数据异常值判定
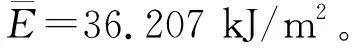
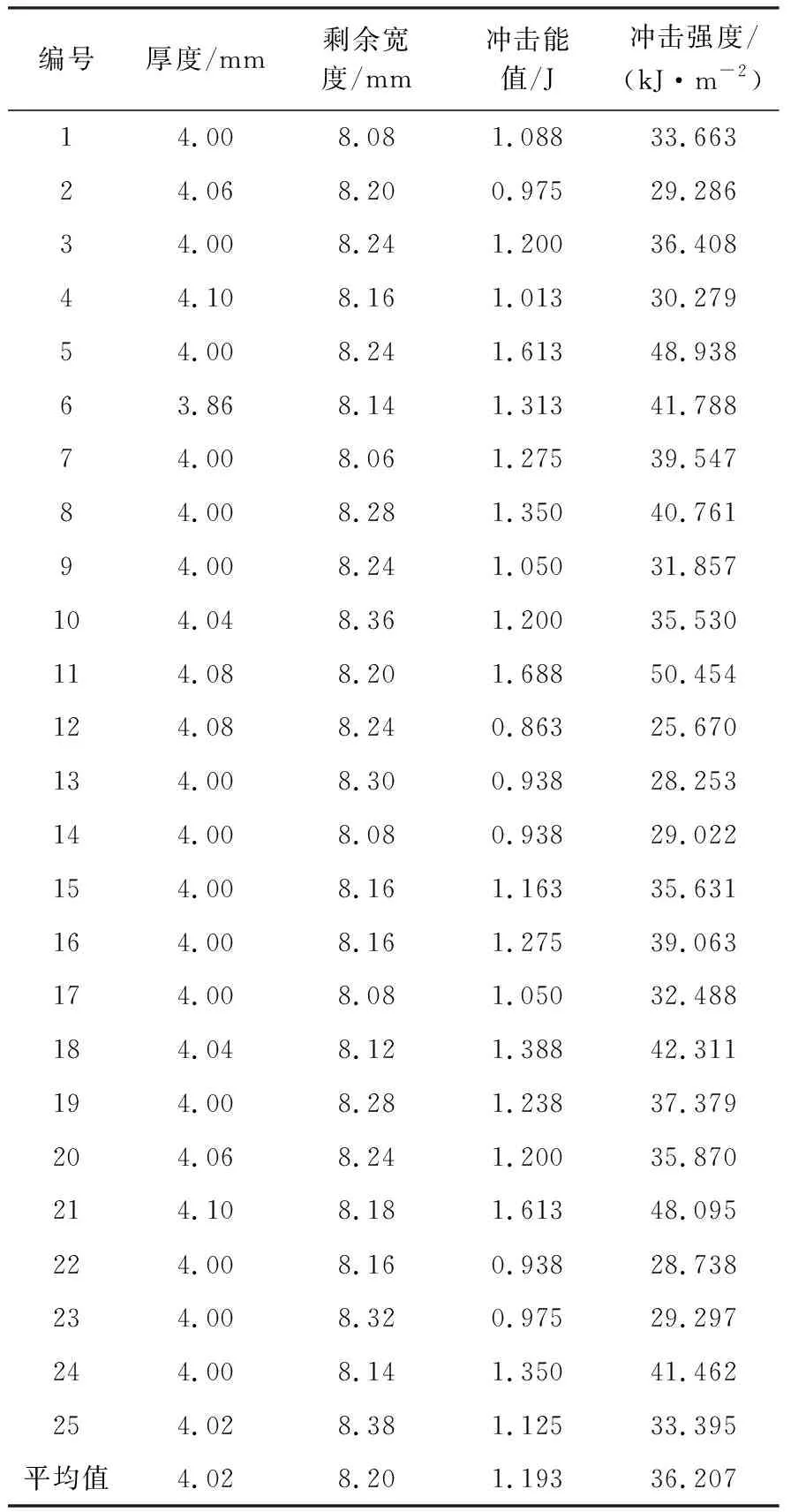
表1 样品冲击测试结果
2.2 不确定度评估
我们首先基于GUM方法评估该型仪器的不确定度。基于此作为对比结果,在2.3中引入贝叶斯方法与Monte-Carlo方法进行对比评估,并详细介绍了其中引起差异性结果的原因。
2.2.1 由冲击样条尺寸测量引入的不确定度
a. 由冲击试样的厚度测量引入的不确定度
利用贝塞尔公式得到25次测量数据的标准偏差:
(9)
故标准不确定度为
(10)
由冲击试样厚度测量引入的相对标准不确定度为
(11)
b. 由冲击试样剩余宽度测量引入的不确定度
同理,基于A类不确定度评估方法评估剩余宽度测量数据,利用贝塞尔公式得到其标准偏差为
(12)
其标准不确定度为
(13)
冲击试样剩余宽度测量引入的相对标准不确定度为
(14)
根据贝塞尔方法计算出的由于冲击样条尺寸测量引入的相对不确定度为

(15)
2.2.2 由于摆锤能量损失而引入的不确定度
a. 与冲击试验机测量误差相关的不确定度
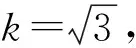

(16)
b. 由于能量损失而引入的不确定度
测试过程中的空气阻力、指针摩擦、轴承摩擦等因素会造成摆锤冲击能损失。参照该试验机技术指标,7.5 J摆锤的能量损失为0.5%,所以区间半宽a=0.5%,测量值落在该区间的概率呈均匀分布,所以相对标准不确定度为
(17)
故在冲击过程中,由于能量损失引入的不确定度为
(18)
2.2.3 由于测量冲击能的重复性引入的不确定度
由贝塞尔公式可计算出冲击强度Ec的标准偏差为
(19)
由于测量的可重复性引入的相对不确定度为
(20)
2.2.4 由于测试数据修约所引入的不确定度
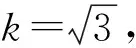
(21)
其相对标准不确定度为
(22)
2.2.5 合成标准不确定度
综合上述几种不确定度分量,将其误差源视为独立分布变量,则合成标准不确定度
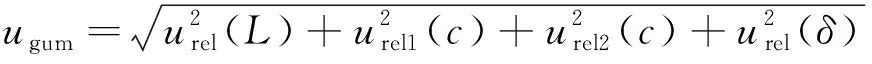
(23)
2.2.6 扩展不确定度
在95%的置信因素下,取包含因子k=2,则扩展不确定度为
uk=k×ugum=10.60%。
(24)
2.3 贝叶斯方法不确定度评估
2.3.1 由冲击样条尺寸测量引入的不确定度
本研究中样条尺寸有25组数据,根据前15组数据得出先验分布,再根据贝叶斯理论计算出后10组数据的标准不确定度。
a. 由冲击试样厚度测量引入的不确定度
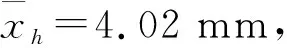
b. 由冲击试样剩余宽度测量引入的不确定度

故根据贝叶斯理论计算出由于冲击样条尺寸测量引入的相对不确定度为
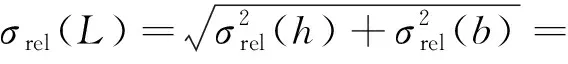
(25)
2.3.2 由于摆锤能量损失而引入的不确定度
贝叶斯方法评估不确定度依赖于先验信息,对于读数误差,损失误差等不可测量的误差因素,其先验信息的缺失可能导致计算数据不足。因此,我们通过Monte-Carlo方法模拟这些不可测量误差从而获得仿真数据,并进一步基于贝叶斯理论计算该不确定度。为模拟真实测量场景,基于上述GUM方法B类评估数据,模拟出M=100万组与测量变量对应的25组误差源数据。并基于贝叶斯方法计算出各个数据源,取其中一组模拟数据(如表2)进行分析。由试验机测试精度引入的不确定度分量σa(c)=3.540 0×10-2,由测试过程能量损失引入的相对不确定度σb(c)=2.815 6×10-3。
2.3.3 由于冲击能测量重复性引入的不确定度
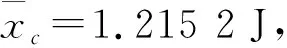

表2 误差模拟数据
因此,由冲击能测量重复性所引入的相对不确定度为σrel(c)=σ(c)/1.215 2=4.907 6×10-2。
2.4 不确定度合成与结果分析
综合上述几种计算源结果,则标准不确定度合成如下:
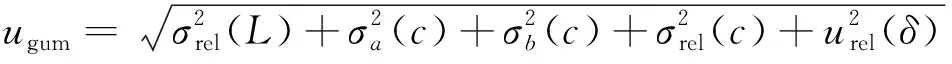
(26)
通过上述计算可知,贝叶斯与GUM方法计算结果存在差异,主要原因在于其先验数据相较于整体测试样本数据未保持分布一致。因此,基于上述分析可知,将BM与Monte-Carlo模拟相结合,并通过多次随机抽取先验数据与后验数据,可有效排除人为因素干扰,有利于获得更为有效的冲击试样测量不确定度评估结果。
2.5 重复随机抽样
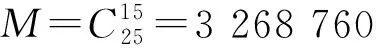
σrel(h)=3.1463×10-3,
(27)
σrel(b)=3.0139×10-3,
(28)
σrel(c)=5.1429×10-2。
(29)
与上述基于贝叶斯方案的结果对比该重复取样方案由于刨除了实验随机选取的影响,因而具有更可信的取样空间,从而计算结果将变得更可靠。
进一步,我们详细分析了不同先验数据比例下(先验与后验数据量的不同)的相对不确定度。在同样实验环境下针对于每组实验模拟M=10万次结果如表3所示。

表3 不同取样尺度的结果
结果项中,由于其选取先验与后验数据数目的不同,导致了最终计算结果的差异。其归因于式(8)受后验数据数目的影响。
3 结 语
本文系统分析了ABS共聚物冲击试样的测量误差源,通过建立完整测量方程,基于GUM标准不确定度评估方法进行不确定度评估。进一步基于贝叶斯评估方法与Monte-Carlo模拟结合评估该型机器的不确定度,并基于结果与GUM标准方法进行对比。利用贝叶斯方法进行了测量不确定度评估。有利于降低试验成本,通过先验数据和后验数据的结合完成大样本量下的不确定度评定,从而获得更为有效的冲击试样测量不确定度评估结果。另外,附加的重复性取样对于贝叶斯不确定度评估也是可选的方法,这将有利于综合先验与后验数据选取的影响。后续将通过实测样本数据以及优化算法进一步提升数据模拟可信度,以此推动和优化冲击试样的标准化研制工作。
